循环载荷作用下高应力岩石疲劳损伤破坏数值模拟与试验研究

赵博，徐涛，杨圣奇，付腾飞

(1.东北大学岩石破裂与失稳研究所，辽宁沈阳，110819；2.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州，221116)

随着开采活动不断走向地球深部，深部岩石力学研究变得愈发重要。在资源开采、能源储存等工程实践中，岩体常受到反复卸荷和加载作用，如深部储油库内部液体的周期性输入输出、煤矿采区工作面的交替推进。这种疲劳荷载作用容易导致岩体发生疲劳损伤甚至破坏，对深部工程的稳定性造成重要的影响。因此，研究高应力岩石在疲劳荷载作用下损伤演化规律对深部工程具有一定指导意义。国内外一些学者对此开展了试验研究，如BROWN等[1]开展了含不同节理类型类岩石材料的峰前及峰后循环加卸载试验研究，揭示了疲劳破坏与残余强度曲线之间的关系。COSTIN等[2]基于裂纹萌生扩展、应力腐蚀和疲劳理论建立了循环压缩载荷作用下脆性岩石的变形损伤破坏模型，并开展了试验对比验证研究。葛修润等[3−4]开展了周期荷载作用下岩石疲劳变形特性试验研究，指出岩石的疲劳破坏受应力−应变曲线控制，疲劳破坏时变形量与周期载荷上限应力在全应力应变曲线后区对应的变形量相当。蔡燕燕等[5]采用不同围压下的应力比疲劳荷载试验分析了大理岩损伤过程中应变率的变化规律；孙爱琴等[6]分析了砂岩在不同应力比循环荷载条件下裂纹扩展位置及数量。CHEN 等[7]对砂岩进行交替循环加卸载蠕变实验，通过分析声发射、轴向及横向应变率的演化规律发现：不同的加载路径对砂岩损伤速率影响较大；徐颖等[8]针对泥岩进行了变荷载循环加卸载试验及等荷载循环加卸载试验，对不同荷载上限疲劳试验中试件的疲劳寿命进行了预测。杨圣奇等[9]开展了不同围压下贯通单节理砂岩的单轴压缩及循环加卸载试验，分析了砂岩的变形特性、强度特性及破坏模式。宫凤强等[10−11]对多种岩石进行了单次循环加卸载试验，发现了加载过程中的线性储能规律。

近年来，一些学者基于数值方法开展了岩石疲劳损伤破坏数值模拟研究。如刘静等[12]利用颗粒流PFC2D进行大理岩三轴循环加卸载，从细观角度观察了裂纹扩展速率及分布随荷载的变化规律；田文岭等[13]用PFC2D模拟煤样在不同围压条件下的循环加卸载，通过分析煤样在加载过程中的弹性模量变化规律及塑性应变演化规律，提出围压增大有利于抑制损伤的产生，同时使试样承受塑性应变能力增大。SONG等[14]基于颗粒黏结模型，提出一种非线性平行黏结应力腐蚀模型，并通过模拟与试验对比分析了非线性应力腐蚀模型的实用性。上述数值模拟都是基于二维模型开展的，而循环加卸载作用下岩石实际上处于三维应力状态，因此，建立三维数值模型更能真实地反映岩石从受载变形至损伤破裂过程中变形特性、力学特性及裂纹在空间中发育扩展的规律。基于此，本文作者在颗粒流PFC3D的基础上引入应力腐蚀模型，建立基于应力腐蚀理论的脆性岩石疲劳损伤数值模型，并对模型进行不同上下限应力水平下的疲劳荷载数值模拟和室内试验对比研究，分析揭示岩石疲劳载荷作用下的变形损伤破坏机理，以期对周期循环及疲劳载荷作用下工程岩体的稳定性分析提供理论参考和应用指导。

1 砂岩疲劳荷载试验

1.1 试验系统

本试验的砂岩采自重庆市万州区，为硬质脆性沉积岩。试样加工成直径×长度为50 mm×100 mm 圆柱形岩样，砂岩物理参数及荷载参数见表1，其中RS-1和RS-2 为单轴压缩试验，其余为疲劳荷载试验，该批岩石试件完整度较高能够有效保证实验的准确性。

表1 砂岩物理参数及荷载参数Table 1 physical parameters and load parameters of sandstone

试验采用美国的GCTS RTR-1000 电液伺服岩石三轴试验系统，该系统主要由加载架、压力室、数字信号调节和控制单元、压力体积控制柜等设备组成，如图1所示。该试验系统具有良好的动、静态特性，能跟踪脆性岩石的瞬间破坏，并自动采集轴向载荷和位移数据，且试样加载过程稳定，自动化程度高，后处理方便。

图1 GCTS RTR-1000岩石试验系统Fig.1 GCTS RTR-1000 rock testing system

1.2 试验方案

在初期压缩加载阶段，采用位移控制的加载方式使砂岩试样内部初始裂纹均匀稳定地压密。在循环加载阶段，选择恒定力控制，为砂岩试样施加稳定的疲劳荷载。本试验选择三角形波的循环加卸载方式，研究不同上下限应力和应力幅值下岩石的疲劳特性，加载频率统一设定为0.2 Hz，以应力比的形式给出应力，应力比为试验设定的应力与岩石单轴抗压强度平均值之比，如上限应力比0.90 即指上限应力为单轴抗压强度平均值的0.90倍。

试验加载波形如图2所示，图中，σmax为周期荷载的上限应力，σmin为周期荷载的下限应力。首先按照0.5 μm/s 等速率加载至下限应力σmin，随后以三角形波进行循环加卸载直至岩样破坏。

图2 三角加载波形Fig.2 Triangle loading waveform

1.3 试验结果

图3和图4所示分别为单轴压缩及部分疲劳荷载试验砂岩的应力−应变曲线，其中，σc为砂岩单轴抗压强度，(0.3～0.90)σc表示应力下限和上限分别为0.3σc和0.90σc。从图3可见：单轴压缩应力−应变曲线包含微裂隙压密、弹性变形、非稳定破裂发展和破裂后4个阶段，砂岩的单轴压缩抗压强度为66.5 MPa。从图4可见：疲劳曲线滞回环呈现出“疏−密−疏”的演化规律。疲劳荷载初期，岩石轴向变形发展较快，滞回环间距较大且比较饱满，说明每个循环消耗了较高的能量，岩石内部损伤量较大。经过数次循环后，岩石变形发展速率逐渐降低并进入稳定增长阶段，滞回环面积明显减小且变得密集，每个循环造成的损伤量大大降低。当试件接近疲劳破坏时，轴向变形速率又迅速增大，短短几个循环造成大量变形，滞回环间距加大。

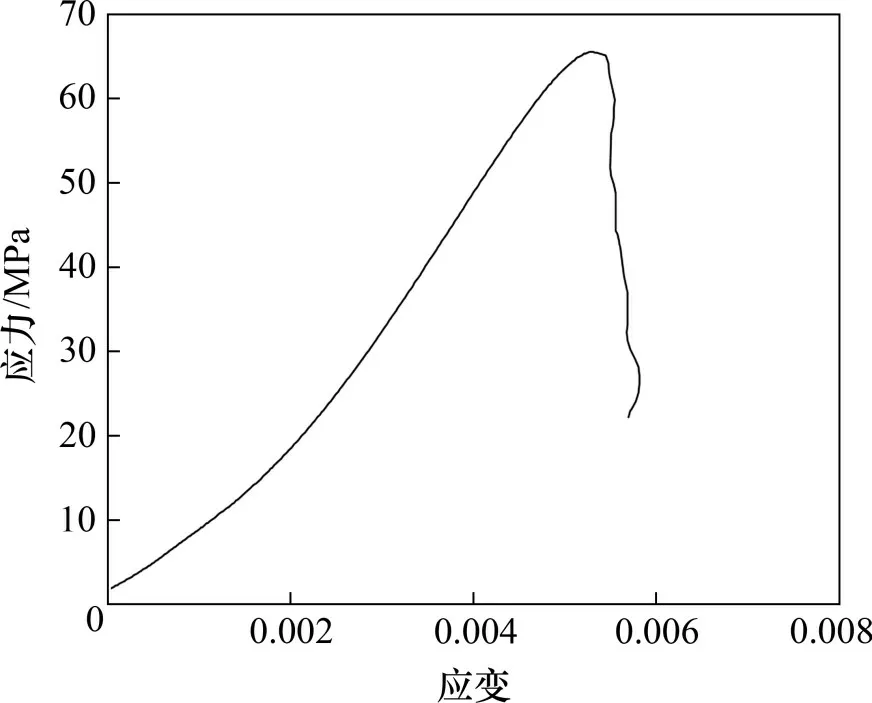
图3 单轴压缩试验结果Fig.3 Uniaxial compression test result

图4 疲劳荷载试验结果Fig.4 Fatigue load test results

2 基于应力腐蚀的颗粒流数值模型

2.1 颗粒流模型

颗粒流程序(particle flow code，PFC)是由CUNDALL[15]开发的一种基于显式差分算法和离散元理论的细观力学程序。该程序处理问题不受变形量限制，处理非连续介质力学问题十分方便，能够有效模拟介质的开裂、分离，反映模型破坏机理和结果。PFC3D中建立的模型主要由球形颗粒或多个重叠的球形颗粒组成的不规则刚性簇构成，每个颗粒都是一个带有质量和表面参数的刚性体，可以产生位移和旋转，颗粒之间通过接触模型产生相互作用。PFC3D模拟计算的基本理论是牛顿第二定律和力−位移准则，在计算求解的过程中基于牛顿第二定律更新墙体和颗粒的位置，通过力−位移准则更新接触力，最终使模型达到平衡状态或者发生损伤破坏。模型中颗粒之间的接触方式采用平行黏结接触，接触处的介质均匀分布，能够传递力和力矩。当接触处作用力超过其黏结强度时，接触处的黏结被判定为断裂，接触处的力、力矩和刚度等力学参数被移除，这与岩石的破裂机制相符。颗粒间接触处的法向应力和切向应力计算公式如下：

式中：和分别为接触处的法向应力和切向应力；和分别为接触处的法向力和切向力；和分别为接触处惯性矩和极惯性矩；||和||分别为接触处的法向力矩和切向力矩；A为平行黏结接触面积(PFC3D中接触为圆形)；为平行黏结接触半径；为转动惯量系数，在PSC 模型中设为1.0。当接触处的>或>时，其中，和分别为颗粒间平行黏结抗拉强度和抗剪强度，程序判定该平行黏结接触破坏，同时在数值模型中移除相应的力、力矩和刚度等力学参数。

2.2 应力腐蚀模型

应力腐蚀模型及腐蚀速率曲线如图5所示，图中，v为应力腐蚀速率。应力腐蚀是指岩石的力学性质随时间不断劣化最终发生失稳破坏的现象。

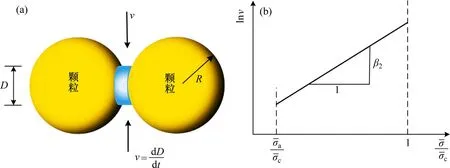
图5 应力腐蚀模型及腐蚀速率曲线Fig.5 Stress corrosion model and corrosion rate curve

POTYONDY 等[16]根据硅酸盐岩石在水的作用下强度不断降低的现象，基于颗粒流PFC 程序提出二维应力腐蚀模型。胡光辉等[17]基于三维颗粒流程序嵌入三维应力腐蚀模型。本文在此基础上应用应力腐蚀模型的思想，通过减少颗粒间的接触直径D来弱化颗粒间接触强度，当颗粒间黏结键受到的应力低于黏结抗拉强度且高于应力腐蚀阈值时，颗粒间的接触直径会随着时间不断减小。在整个伺服的过程中，模型内部接触力分布不断更新，并移除破坏(接触力超过黏结强度)或者完全溶解的黏结键。

应力腐蚀模型中判断黏结键是否发生应力腐蚀及应力腐蚀速率计算公式如下：

式中：为应力腐蚀阈值；β1和β2为材料常数。

本文引入离散裂隙网络(discrete fracture network，DFN)记录试样在疲劳损伤过程中裂纹产生的空间位置及数量[18−19]，将每次黏结键的断裂视为一个微裂隙的产生，通过统计生成的微裂纹数量、位置和方向等信息以监测砂岩在疲劳损伤过程中细观演化规律。

2.3 细观参数标定

模型按照实验标准试件(直径×长度为50 mm×100 mm)建立，然后判断并消除模型内部的悬浮颗粒来提高模型的准确性，最后在模型范围内建立3个均匀分布的测量球用来测量模型的应变及内部应力。由于PFC 是根据局部接触来控制宏观力学特性的，因此进行模拟计算时需要通过定义颗粒和接触的微观几何参数和力学参数来反映宏观的力学参数，但是目前还没有方法来确定宏观参数与微观参数之间的关系，因此基于室内试验结果，利用试错法进行细观参数标定。细观参数标定分为瞬态细观参数标定和时效细观参数标定2 个步骤。

1)瞬态细观参数标定。通过单轴压缩试验，测得砂岩试样的峰值应力为66.5 MPa、弹性模量为15.9 GPa、泊松比为0.26。利用试错法标定颗粒细观参数和接触细观参数使数值模型表现的宏观力学性质与室内岩石试件的力学参数相匹配，标定的瞬态力学参数如表2所示。单轴压缩条件下室内实验与数值模拟的应力−应变曲线及破坏模式如图6所示。

图6 单轴压缩试验结果Fig.6 Uniaxial compression test results

表2 数值模型细观参数Table 2 Micro-parameters of numerical model

由于室内试验的砂岩试样中含有大量原生微裂隙，在加载初期，这些微裂隙在压力作用下闭合，导致岩石弹性模量增加，应力−应变曲线上凹。建立的数值模型中不含原生微裂隙，因此得到应力−应变曲线没有初始压密阶段。为了方便室内实验结果与模拟的结果进行对比，将室内实验得到的应力−应变曲线的倾斜直线部分延伸直至与X轴相交，再将曲线整体向左平移至原点[20]。经过处理后的室内试验与数值模拟的应力−应变曲线能够较好吻合，且形成了类似的倾斜宏观断裂面，说明本文建立的模型能够有效反映砂岩试样的力学特性及变形特性。

2)时效细观参数标定。根据不同应力水平下砂岩试样的单轴压缩蠕变试验结果标定时效细观参数，其中材料常数β1为14×10−15、材料常数β2为11、应力腐蚀阈值为10 MPa。70%应力水平下的室内试验与数值模拟的单轴压缩蠕变结果如图7所示，模拟结果再现了蠕变的3个阶段[21]：初始蠕变阶段、等速蠕变阶段和加速蠕变阶段。数值模拟与室内试验的蠕变曲线能够较好地吻合，数值模型微裂隙的空间分布与试验中试样破裂时形成的宏观破裂面相照应，体现了所标定的时效细观参数的合理性。

图7 单轴蠕变试验Fig.7 Uniaxial creep test

3 数值模拟

3.1 不同上限应力比分析

在疲劳荷载过程中，应力水平是影响岩石疲劳寿命的重要因素。为了分析不同上限应力对岩石力学特性及变形特性的影响，恒定下限应力比为0.3、设置不同上限应力比分别为0.80，0.85和0.90，模拟砂岩的疲劳损伤破坏。不同上限应力比条件下应力−应变曲线如图8所示。由图8可见：不同上限应力比条件下，应力−应变曲线的滞回环均呈现出“疏−密−疏”的演化特征。初始阶段常常只有几个循环，占整个疲劳寿命的小部分，这个阶段滞回环的面积及间距相对较大，每个循环消耗较多能量，轴向变形速率也较大。随后疲劳损伤稳定发展，轴向变形随着循环的进行呈线性增长规律，变形速率明显比初始阶段时的小，且滞回环数量密集、面积较小，这个过程占据疲劳寿命的绝大部分。随着循环次数的持续增加，模型内部微裂隙不断发育，当损伤积累到一定程度形成贯通裂隙时，试样发生加速变形，模型轴向变形迅速增大，变形速率达到最大值，滞回环的面积及间距再次变大。

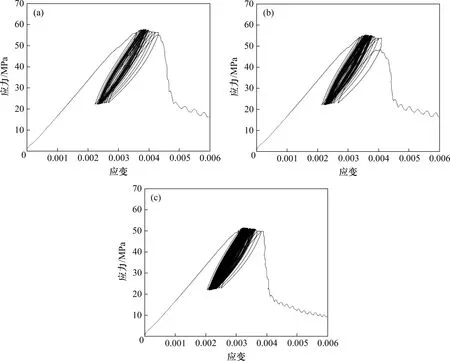
图8 不同上限应力比条件下应力−应变曲线Fig.8 Stress−strain curves of different upper limit stress ratios

当上限应力比为0.90 时，模型在循环22 次后发生失稳破坏，稳定循环荷载阶段的滞回环面积明显比其余两组的大，且滞回环之间的间距也更加稀疏；当上限应力比为0.85 时，模型在循环35次后塑性应变迅速增大直至破坏；当上限应力比为0.80 时，滞回环的面积及间距最小，循环63 次后试样发生破坏。由此可见，当疲劳荷载下限应力保持不变时，上限应力越大，滞回环的面积和间距越大，每次循环损伤累计越多，岩石越容易发生损伤破坏。

3.2 不同下限应力比分析

恒定上限应力比0.85、设置不同下限应力比分别为0.3，0.4和0.6，模拟砂岩的疲劳损伤，模拟结果如图9所示。可见：当下限应力比为0.3 时，试样经过35 次循环发生失稳破坏；当下限应力比为0.4时，试样经过41次循环发生破坏；当下限应力比提升至0.6时，滞回环曲线面积和循环间距明显减小，试样经过72次循环发生破坏。由此可见，当疲劳荷载上限应力保持不变时，滞回环的面积和间距会随着应力下限水平的上升而减小。这是因为下限应力水平大幅度提高，相当于大幅度减小振幅，造成每次循环产生的塑性应变减小，裂纹闭合和张开较小，因此达到破坏所需的循环次数相应更多。

图9 不同下限应力比曲线Fig.9 Curves of different lower limit stress ratios

3.3 裂纹扩展分析

为了分析疲劳荷载过程中试样内部裂纹发育及扩展情况，以及不同应力水平对岩石损伤积累的影响，研究不同上限应力比及不同下限应力比模拟的裂纹数量随加载时间步的变化规律，结果如图10所示。

从图10可以看出：不同应力条件下，试样的损伤积累曲线形态基本一致，分为3个阶段：1)初始疲劳荷载阶段：随着应力的不断增加，试样内部薄弱部分难以承受较高的应力水平作用而迅速破坏产生裂纹；2)稳定扩展阶段：随着疲劳荷载不断作用，颗粒间的接触强度由于应力腐蚀作用不断弱化，裂隙数量呈阶梯状缓慢增加；3)加速破坏阶段：微裂隙不断增加，最后贯穿导致模型迅速破坏，产生宏观破裂面。从图10(a)可以看出：当下限应力比恒定时，随着上限应力比的增大，模型裂纹扩展速度快速增加，失稳破坏的时间也随之缩短。当上限应力比从0.80 提高到0.85 时，模型的疲劳寿命缩减了38.1%；当上限应力比为0.90时，模型的疲劳寿命缩减量提升至60.4%。从图10(b)可以看出：当上限应力比恒定时，虽然疲劳荷载循环次数随着下限应力水平增大而增多，但调整下限应力比对模型损伤破坏时间影响较小。这是因为在PFC 模型中，接触间的应力腐蚀速率与接触之间的应力成正比，应力上限保持不变的情况下，应力腐蚀最大速率也会保持不变，而接触之间的应力低于一定水平就不会发生应力腐蚀现象。因此，上限应力水平保持不变，调整下限应力水平对模型损伤破坏时间影响不大，说明影响模型损伤破坏时间最主要的因素是应力上限水平。

图10 裂纹扩展比较Fig.10 Comparison chart of crack growth

3.4 模拟与试验对比

选取(0.3～0.90)σc，(0.3～0.85)σc，(0.6～0.85)σc疲劳载荷作用下室内试验和数值模拟结果进行比较，如图11和12所示。为了便于对比分析，同样把试验曲线初始压密阶段去除并平移，处理后的试验曲线与模拟曲线重合度较高，且满足疲劳破坏曲线与单轴压缩曲线之间的关系(图11)。此外，模型与试验试件破坏模式一致，宏观破裂面均以斜对角线为主(图12)。说明建立的模型能够较好地反映岩石宏观力学性质及疲劳荷载状态下的损伤演化规律。

图11 模拟与试验应力−应变曲线对比Fig.11 Comparison of numerical simulation and experimental stress−strain curves

图12 模拟与试验破坏模式对比Fig.12 Comparison of simulated and experimental failure mode

4 结论

1)疲劳荷载作用下，试样的应力−应变曲线中滞回环呈现出明显的“疏−密−疏”的演化特征，即初始加载作用下，模型塑性变形较大，滞回环面积和距离都比较大。随后进入稳定疲劳荷载阶段，塑性变性发展缓慢，滞回环变的密集。随着损伤不断累积，达到一定程度后模型塑性变形迅速增大，直至失稳破坏，这个阶段滞回环再次变得饱满稀疏。

2)当保持下限应力水平不变时，上限应力水平越大，滞回环的面积和间距越大，塑性变性累计越快，相应循环次数也越少；当保持上限应力水平不变时，下限应力水平越大，应力水平幅值越小，则滞回环的面积和间距越小，每次循环造成的塑性变性越小，相应达到破坏时循环次数越多。

3)疲劳荷载作用下，试样内部裂纹扩展呈现3个阶段，整体呈阶梯状增长。当保持下限应力水平不变时，模型的疲劳寿命随着上限应力水平的增加快速减小，但是保持上限应力水平不变时，虽然循环次数仍有差距，但是损伤破坏时间却相差不多，说明上限应力水平是控制模型疲劳寿命的最主要因素之一。