基于随机矩阵理论的局部放电脉冲快速检测方法

徐友刚，陈敬德，陆敏安，曹基南，沈晓峰，罗林根

(1.国网上海市电力公司青浦供电公司，上海 200437；2.上海交通大学电气工程系，上海 200240)

很小的绝缘缺陷在电力设备带电运行状态下会由小变大，最终可能诱发整体的绝缘性故障，造成大面积停电，给国民经济带来损失。对局部放电(partial discharge,PD)的检测及定位对及时发现绝缘缺陷的重要手段之一，对电力设备检修有重大意义[1-2]。

由于受变电站现场复杂环境的影响，测试现场往往充斥着电、磁、声音等背景噪声，对局部放电信号的检测带来了很大的困难。实践中发现局放信号往往淹没在噪声中，并且，由于信号与频率存在重叠，以至常用的频域分离方法的去噪效果不佳。为此，相关学者研究并提出了一系列抑制噪声影响的方法并取得了较好的应用效果[3-6]。由于无法预先知道所采集的数据中是否存在局部放电脉冲，所提出的噪声抑制算法往往需要针对所有采集的数据展开。在数据量特别大的时候，例如特高频电磁波信号等，将严重影响去噪算法的实时性。一种常用的方法是对数据进行加窗，再对每个数据窗进行去噪处理。同样地，由于无法预知每个数据窗是否存在局放脉冲，还是需要对每个数据窗进行处理。因此，提出一种基于随机矩阵理论的局部放电脉冲快速检测方法，实现对数据窗口中是否存在放电脉冲的快速检测。这样就只需存在放电脉冲的数据段进行各种数据处理运算，从而降低数据量、提高实时性。

随机矩阵理论[7](random matrix theory,RMT)是一种处理大维数据的有效方法，在无线通信信道估计、神经网络、网络容量分析及频谱感知[8-11]等领域均有广泛应用。近年来，RMT的最新研究成果——非渐近随机矩阵理论[12-13](non-asymptotic RMT)可以很好地解决有限维问题，将RMT从无穷维理论分析推向有限维实际应用。另外，由于经典随机矩阵理论是针对服从高斯分布数据的分析方法，现将局部放电数据等效为时间序列，应用扩展的随机矩阵理论中谱分布特性来实现局放脉冲的快速识别。

1 随机矩阵理论及ARMA模型的随机矩阵谱分布理论

1.1 Marchenko-Pastur定律

设X={ξij}1≤i≤N,1≤j≤n是一个N×n维随机矩阵，矩阵内的元素服从方差为σ的独立同分布。该矩阵的维数还满足N/n=c∈(0,1]。相对应的协方差矩阵S=1/n(XHX)的经验谱密度(empirical spectrum density,ESD)将收敛于Marchenko-Pastur定律(M-P律)[7,12]，表达式为

(1)

1.2 ARMA模型的随机矩阵谱分布理论

现场测试环境的背景噪声复杂，既存在着高斯白噪声，也有定频干扰、脉冲干扰等。因此，用高斯模型对噪声进行模拟，不符合实际情况。采用自回归滑动平均(autoregressive moving average model，ARMA)模型对背景噪声进行模拟并研究该模型下的随机矩阵谱分布规律。设时间序列xt为ARMA(p，q)过程，φ(B)xt=θ(B)εt，其中p、q为ARMA模型的阶数，εt为服从N(0,σ2)分布的噪声。而φ(B)=1-φ1B-…-φpBp，θ(B)=1+θ1B+…+θqBq是关于B的多项式，其中B为延迟算子，Bjxt=xt-j。则时间序列xt的功率谱密度[14]为

(2)

式(2)中：ω为角速度。则其样本协方差矩阵的计算公式为

(3)

式(3)中：xi=(x1i,x2i,…,xpi)T。协方差矩阵特征值的经验谱分布表达式为

(4)

式(4)中：λt(t=1,2，…,p)为协方差矩阵Sn的特征值；I(·)为指示函数。

对于式(4)中提到的经验谱分布，Stieltjes变换可表示为

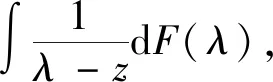
z∈C+:={z∈C:Imz≥0}

(5)

若满足以下条件：

(1)维度p趋近于正无穷，数据量n趋近于正无穷，p/n→c∈(0,∞)。

(2)随机误差限定于4次时间维度内，即

(6)

(3)线性滤波器(φk)是绝对可加的，即

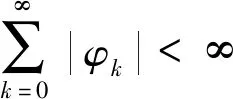
(7)

则可以肯定经验谱分布函数一定存在极限谱分布，Stieltjes变换s=s(z)满足以下逆变换[14-15]，即

(8)

(9)

2 局部放电时间序列实时化高维随机矩阵构造方法

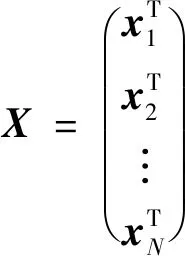
(10)

X是N×T随机矩阵，可以通过改变采样频率和采样时长来调整矩阵X的行列数比值，以保证矩阵X满足随机矩阵理论分析的要求。

对于一组连续采样，向量x可以按时间顺序组合成矩阵。一般来说，原始数据都是连续采样的，通过一个分割窗口截断测量数据从而构成原始数据矩阵X∈CN×T用于后续分析。值得注意的是用于组成矩阵X的分割窗口长度是N×T，并且T也被定义为用于连续实时处理的移量。参数T可以根据实时处理要求进行调整。数据处理的一般框架如图2所示。

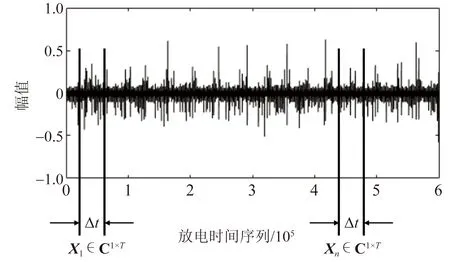
图1 PD信号的高维随机矩阵构造Fig.1 Constructing high dimensional random matrix of PD signals

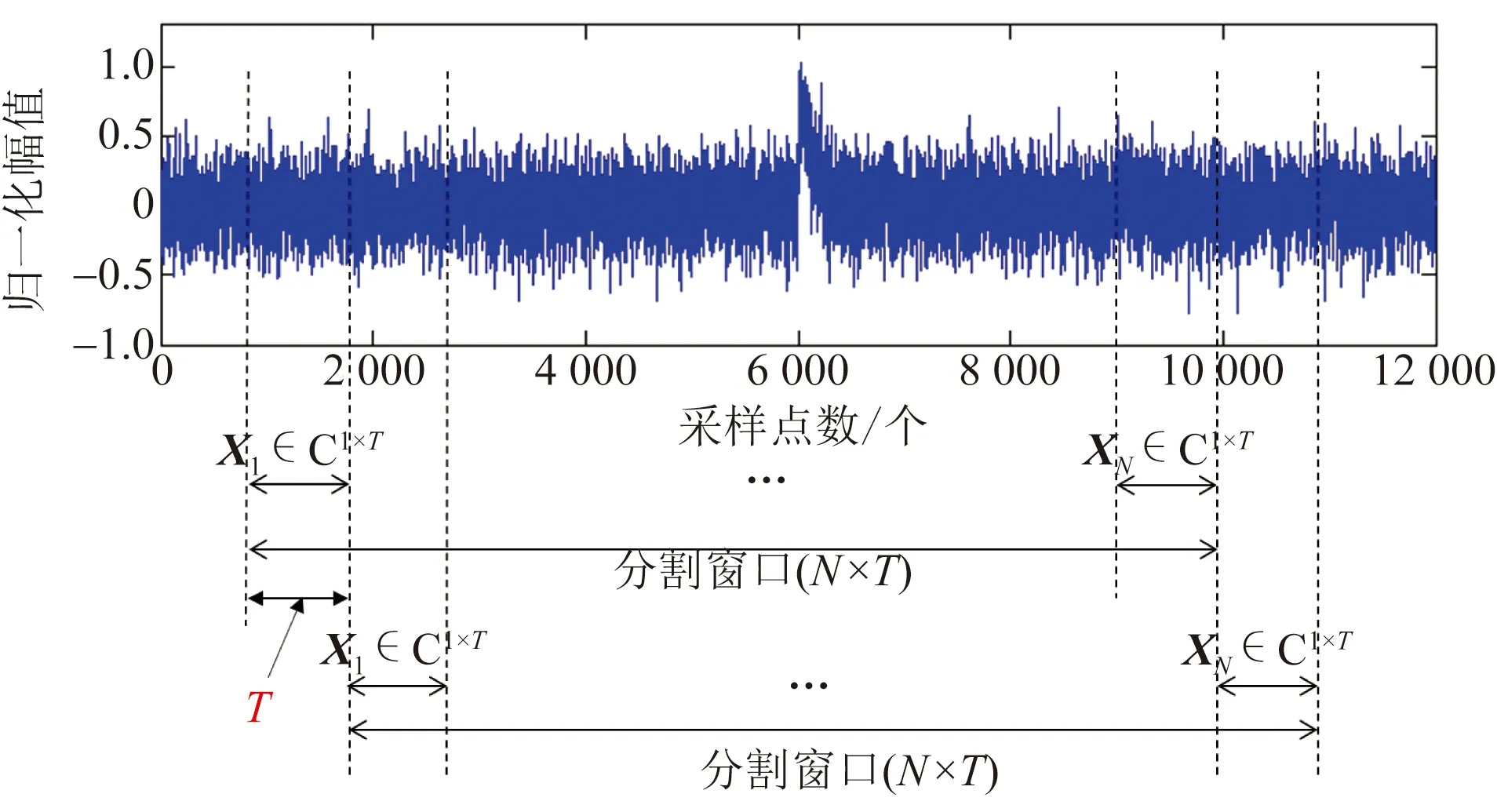
图2 实时数据处理框架Fig.2 A real-time data processing framework

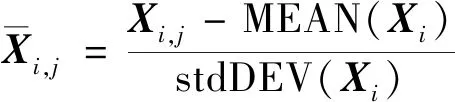
(11)

式(11)中：MEAN(Xi)为向量Xi的均值；stdDEV(Xi)为向量Xi的标准差。

图3给出了含PD信号时间序列依照图2所示方法生成的1 000×250随机矩阵的经验特征值分布。从图2中可以看出，该矩阵的特征根分布渐进收敛于一个确定区域内。特别地，由于该时间序列中含有PD脉冲信号，表现在特征根谱分布中存在着一个特征根值明显不在收敛区间(如图3中箭头所示)。这一特性为PD脉冲检测算法提供理论支撑。

3 快速脉冲检测

受到图3所示的时间序列所构成随机矩阵谱分布特性启发，提出了一种用于快速PD脉冲检测的最大特征值观测方法，算法步骤如下。

(1)根据选择的偏移长度T和分割窗口长度N×T，利用第二节所示的方法获得矩阵X。

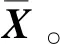
图3 含PD信号的1 000×250随机矩阵的经验特征值分布Fig.3 Empirical eigenvalue distribution of a 1 000×250 random matrix in case of a signal present

(4)计算矩阵S的特征值。

(5)对特征值进行降序排列，得到最大特征值。

(6)通过偏移量T移动分割窗口以生成下一个矩阵，然后转到步骤(1)继续执行直到原始数据集的结尾。

(7)根据每次计算所得最大特征根谱的突变计算所对应的偏移量，从而得到PD脉冲位置。

4 仿真验证

用双指数衰减震荡函数[16]来模拟电力设备的PD信号进行分析，表达式为

f(t)=Am[e-τ1(t-td)-e-τ2(t-td)]sin(2πfct)

(12)

式(12)中：Am为幅值；τ1、τ2为衰减系数；fc为中心振荡频率；td为PD信号的起始时间。图4(a)给出了在A为0.7，τ1与τ2分别为2 μs和0.2 μs，td为6 000 μs且采样率fc为1 MHz的情况下的PD模拟信号。叠加的高斯信号的信噪比(signal to noise ratio，SNR)为-10 dB。此外，两个幅值分别为0.2 V和0.6 V，频率分别为0.1 MHz和1.5 MHz的正弦信号模拟窄带干扰被加入PD信号中。图4(b)和图4(c)分别给出了叠加高斯干扰及定频干扰后的PD信号，其中PD信号长度为12 000个采样点，将作为本算法性能验证的原始数据。

滑动偏移长度T选为100，分割窗口长度N选为4 000，构成的矩阵应是40×100的矩阵，记为X。其对应的协方差矩阵为S=1/40(XXH)。

图5左半部分给出了由分割窗口产生的矩阵X的特征值分布(直方图)。可以看到矩阵S的特征值分布基本上遵循M-P定律(蓝色曲线)，除了图5右侧所指的最大特征值。这是因为分割窗口中的波形包含两个正弦干扰信号，即意味着干扰信号不是纯高斯分布噪声。

图4 模拟PD信号Fig.4 Simulated PD signal

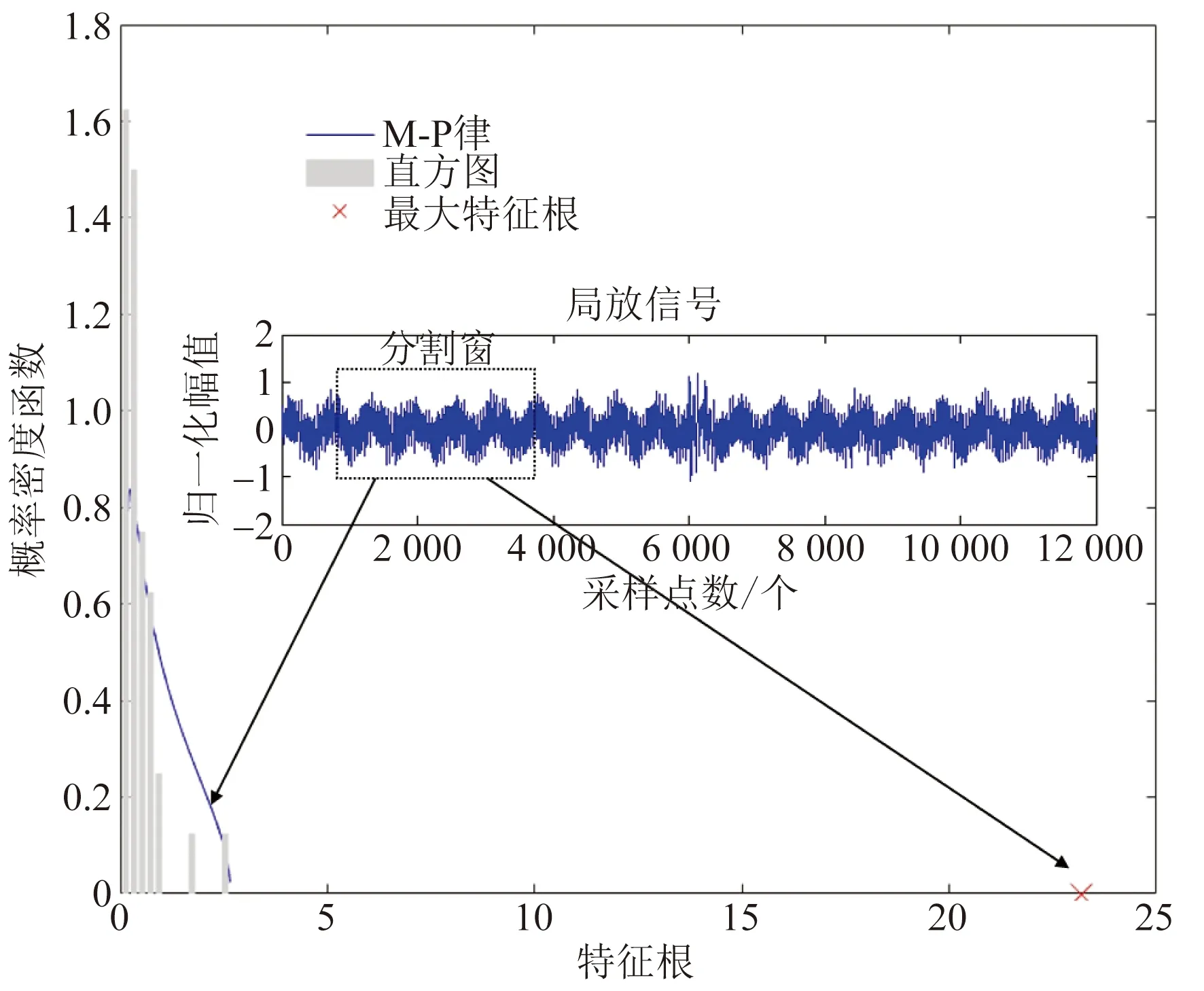
图5 模拟局放信号的M-P律与特征值分布间比较Fig.5 Comparison between M-P law and eigenvalue distribution of analog partial discharge signals

随着分割窗口逐渐向右滑动，可得到每次生成矩阵X的最大特征根序列，图4(c)所示仿真数据的最大特征根演化特性如图6所示。从图6中可以看出，最大特征值的突变(即黑色框中的红圈)是和PD脉冲同时出现的。PD脉冲出现在采样点6 000点处，最大特征值突变点出现在约22个偏移单位处，意味着在该时刻的分割窗口包含采样点2 200点(T×22)到6 200点(T×22+N)。因此可以看出，随着矩阵S的最大特征值的演化，可以通过其突变位置快速地识别出非高斯噪声(高斯噪声叠加固定频率干扰)下的PD脉冲位置。

图6 基于最大特征值演化的PD脉冲检测方法Fig.6 The maximum eigenvalue evolution according to the sliding split window for PD pulse detection

5 试验验证

为进一步验证所提算法的可行性，开展了如图7所示的局部放电试验，以采集真实PD信号用于测试。

通过实验收集了悬浮放电、微粒放电、沿面放电和针尖放电4类典型绝缘缺陷局部放电数据各20组。每组放电数据与仿真数据一致，即长度为12 000个采样点。试验结果如表1所示，由于悬浮放电和针尖放电的放电幅值比较大，相应地，其信噪比较高，PD脉冲位置检测效果明显，20组数据均能准确识别PD脉冲位置。而沿面和微粒放电幅值特别小，其信噪比很低，但本文方法也能达到90%以上的识别正确率，为后续的信号处理奠定基础。

图7 局放试验系统示意图Fig.7 Schematic diagram of PD test

表1 PD脉冲检测结果Table 1 Results of PD pulse detection

6 性能比较

实际应用中常采用阈值法对可能存在局部放电脉冲的数据段进行筛选。当检测到信号大于预先设定的阈值时，该时刻前后一段数据即认为可能存在局放脉冲的数据段。为对比分析本文所提算法的性能，采用阈值法对相同的20组试验数据进行局放脉冲检测，结果如表2所示。

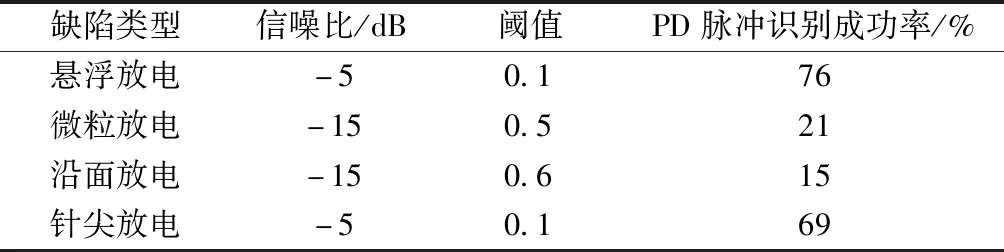
表2 基于阈值法的PD脉冲检测结果Table 2 Results of PD pulse detection based on threshold method

从表1和表2结果可以看出，在信噪比较高的情况下，一般可将阈值设定为较小的值来区分信号与噪声。阈值法对悬浮和针尖放电数据的脉冲识别率不到80%，显著低于本文方法。而在信噪比较低的情况下，阈值法难以有效区分放电脉冲。由于阈值法只是简单地采用一个数值来区分信号和噪声，如果设置的阈值较大，则会遗漏掉幅值较小的局放脉冲信号；如果阈值设置较小，则起不到对数据是否含有局放脉冲的预判功能。

7 结论

提出了一种基于随机矩阵谱分布理论的局部放电脉冲快速检测新方法，能快速识别数据段内局部放电脉冲的位置，从而有效降低了后续数据处理算法的运算数据量。仿真和试验结果证明了算法的可行性和准确性，同时，所提算法在低信噪比环境中具有很好的鲁棒性。另外，该算法计算量非常小，正如文中算例所示，仅需计算一个40×100矩阵的特征值，便于现场应用。