从有意思走向有意义
——《三位数乘两位数的练习课》教学设计
文|林志辉(特级教师) 陈柯柯
【教前思考】
数学基本思想归结为三个核心要素:抽象、推理和模型。“数”本就是抽象后的存在,计算是具体的推理,推理是抽象的计算。本节课是人教版四年级上册第四单元“三位数乘两位数”的练习课,在本节课前已进行了三位数乘两位数笔算和因数中间、末尾有0的笔算乘法,本节课之后将进行积的变化规律的教学。本节课是一节计算练习课,如何把一节计算练习课上的既有意思又有意义?笔者主要学习和思考了以下两个问题。
思考之一:计算练习课的意义何在?
计算教学其本质都是在计算计数单位的个数,而乘法计算的本质就是计数单位的累加过程。这个累加的过程便是算理的理解。算理的理解、思维的提升、运算能力的培育不是新授课的物理叠加就能实现的,此时练习课的出现就显得尤为必要。作为新授课的延伸,为学生提供了系统深化、内化的时间与空间,此为计算练习课的意义之一。
数学知识是一个充满了联系的体系,计算教学也是如此,数的运算就包括四个方面,四者不是孤立的存在,每个知识之间都有着内在的联系。作为一节计算练习课,核心追求肯定是发展学生的运算能力,但往往武断地将运算能力等同于运算与方法技巧的熟练。运算能力主要是指能够根据法则和运算律正确地进行运算的能力。运算能力是运算技能与逻辑思维等能力的有机整合,不仅是一种数学的操作能力,更是一种数学的思维能力。培养运算能力,此为计算练习课的意义之二。
思考之二:计算练习课如何有意思?
怎样的数学课是有意思的?笔者以为学生学习自主性得以唤醒,学习积极性得以激发,能感受数学的自身魅力,学有所思、学有所得的课堂才是有意思的。课堂的主人是学生,学生的认知起点决定了课的原点,学生已经掌握了三位数乘两位数笔算乘法的算法,感悟了算理,形成了一定的计算法则,这就决定了本节课更不能唯法则机械运算。计算有三宝———口算、估算、笔算,三者的灵活运用是检验运算能力有效落实的一项标准。笔者思考,能否基于简约的素材,经历本质的探究,发展高阶思维,培育核心素养,实现从动手算走向动脑想?于是便有了《三位数乘两位数的练习课》的实践。
【教学过程】
一、善辨析,三算不分家
师:(出示123×45)这是一道三位数乘两位数,会算吗?
(全班学生纷纷举手)
师:看来太简单了,没意思,来道难的!(出示□□□×□□)
生:老师你给我们些数据吧!
师:数据来了!(出示四个选项①998②6660③99901④100000)可能等于多少呢?你会选谁,不选谁?说明你的理由。
(学生活动,反馈)
1.反馈口算。
生:我不选①号,你们猜我是怎么想的?
生:我觉得你可能想到100×10=1000,三位数乘两位数最小都是1000,998肯定不对。
师:你们用了口算来说明,真会思考!
2.反馈估算。
生:我的理由是1000×100=100000,你们猜我肯定不选什么?
生:最小的四位数乘最小的三位数才等于100000,所以肯定不选④号。
生:我们还可以这样想,最大的三位数乘最大的两位数999×99,都往大了估才到100000,肯定不是④号。
师:他们又用了什么方法来说明?
生:可以口算也可以估算,都往大了估发现还不行,肯定不选④号。
生:我写了999×100,你们知道我是怎么想的吗?
生:我想你用了口算的方法,肯定不选③号。因为最大的三位数999乘最小的三位数100都比③号小,③号大了,肯定不选③号。
生:也可以用估算的方法想,999×99,把99往大了估成100都比③号小,所以肯定不选③号。
3.反馈笔算。
师:你们可真有办法,那到底999×99等于多少呢?
生:我是笔算算出来的。
(呈现学生作品)
师:算对了吗?
生:我重算了一次,是这样的。
生:我口算了一次,999×100=99900,多算了一个999,那么99900-999=99900-1000+1=98901。
师:(指着竖式中的计算过程)都是8991,表示什么意思?
生:第一个表示8991个一,第二个表示8991个十,它们不一样!
4.确定范围。
师:刚才同学们用了口算、估算、笔算说明①号、③号、④号选项肯定不行,那三位数乘两位数到底能算出几位数呀?
生:最小四位数,最大五位数。

【设计意图:通过“□□□×□□=?”的选择题入手,“选谁,不选谁并说明理由”的任务一下子就吸引了学生的注意力,四个选项是经过笔者比较思考的,①998②6660③99901④100000作为三位数、四位数、五位数和六位数的代表,因其接近整百整千,学生自然想到利用估算和口算进行排除,学生在辨析的过程中经历“口算筛选-估算比较-笔算验证”,三算的出现成了学生的内需,三算的糅合成了选择的需要。】
二、细观察,规律来初探
师:□□□×□□=6660,像这样的算式你最多能列几道呢?
生:我列了一道666×10。
生:我列了四道,666×10,111×60,333×20,222×30。
生:我只写了六道,但我觉得如果再写下去我可以写出无数道,111×60、222×30、333×20、444×15、555×12、666×10……
师:谁看明白他的想法了?
生:第一个乘数都是多了111。
生:他是把第一个算式当作标准,第一个乘数乘几,那么第二个乘数就除以几。
生:我赞同你的想法,如果只是看加减,第一个乘数加了111,但第二个乘数就没有这样的加减规律了。
师:这可是后续要学习的积的变化规律,你们可太厉害了!
【设计意图:史宁中教授说过“好的结论往往不是证出来的,而是看出来的。”学生在“最多能列几道?”问题的驱动下,学习的兴趣被激发,通过观察、比较发现算式间的内部规律,为后续学习积的变化规律积累了丰富的感性认知和活动经验。】
三、巧编题,范围精确定
师:看来这样的题目对我们班的同学来说太简单了,我把题目变一变,约等于6000,你还能继续编吗?看看谁编的更接近!
1.自主编题。
(学生活动,上台板书算式)①600×11②201×30③100×59④199×30⑤601×10⑥102×60
师:符合吗?谁的更接近?
生:都符合,但是其他都是乘数增加或减少1,⑥号增加了2,所以我排除⑥号。
生:我认为①号更接近,他是想着600×10,然后10多了个1。
生:那⑤号也是想着600×10,600多了个1,也就是多了1个10,①号都多了1个600了。
生:对,我还发现其实②号和④号一样,一个多了30,一个少了30。
生:我发现在三位数上增加或减少会更接近,大家看,①号多在第二个乘数,结果多了600,⑥号多在三位数,都多了2了,结果增加了2个60,也就是120,比①号还小。
生:根据你的方法我排除了①号和③号,我发现,其中⑤号的第二个乘数最小,所以我认为⑤号最接近。
生:我赞同他的想法,我还能再写一个和⑤号一样接近的,599×10。
【设计意图:比较是一切理解和思想的基础,通过逆向填写乘数,编写“□□□×□□≈6000,谁编的更接近?”学生不断运用口算、估算反复尝试、反复思考比较,为了找出最小的,学生思考范围由大及小,甚至偷偷笔算,更难能可贵的是,学生通过比较增加三位数和增加两位数对结果的影响,比较增、减乘数对范围的影响,尝试用语言进行概括,他们的语言也许较为稚嫩,但却触及本质,对计数单位的累加感悟深刻。】
2.推理辨析。
师:你们太会思考了,我也写了三道,哪道更接近呢?①601×13②299×21③198×32
师:你肯定不选谁?
生:我肯定不选①号,②号和③号的乘数只要一个增加,另一个就减少,就①号全部增加。
生:我不选①号,因为①号都多了将近3个600了,太多了!
师:到底是②号还是③号?
生:我觉得应该选②号,③号看似扯平了,增加2个减少2个,但是②号毕竟才增加1个减少1个。
生:②号是想着300×20,299×21就是20个299再加上1个299,和20个300比较,那就是多了一个299,少了一个20,也就是总的增加279。
生:那么③号就是增加2个198,减少2个30,也就是总的增加336,肯定②号更接近。
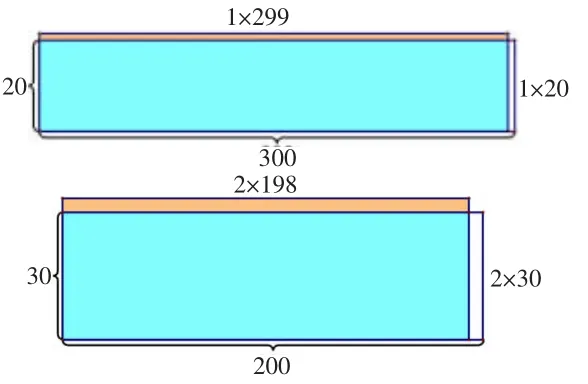
【设计意图:笔者设计的三个选项打破了学生的思维定势,在推理的过程中让学生充分感悟估算的价值。其中①号选项承接学生编题中的经验,将两个乘数都变大,将第二个乘数增加了3,学生迁移原有认知能较为轻松地辨析出来。而②号和③号,乍看之下一个乘数减少多少,另一个乘数就增加多少,形成了一定程度的互补,但这样的互补仅限于乘数相加和不变,在乘法模型中的不适用打破了学生的思维定势。但从动手算走向动脑想,对学生来说是存在一定难度的,为了让更多的学生感受到数经过运算后的变化,深入理解算理发展数感,通过几何直观面积图的介入,将抽象的运算过程动态可视化的呈现,破解学生理解的难点。】
四、重梳理,联结齐厘清
师:今天我们学习了三位数乘两位数,这是整数乘法的最后一节课,为什么以后就不学了呢?
生:因为都一样,如果是三位数乘三位数,就是多算一层,也就是多算几个百,然后加进去。不管多大的数相乘,其实就是增加或者减少几个几的问题。
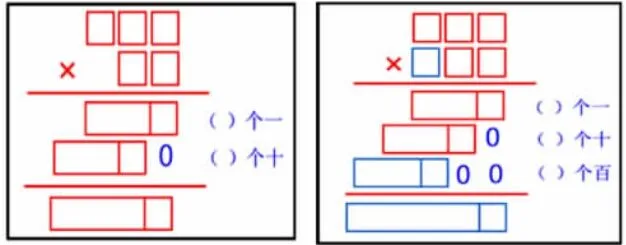

【设计意图:学习贵在求联,网络化、系统化的将知识进行打通梳理,学生在比较整理中发现乘法的运算就是计数单位的累加过程,真正触摸到了乘法的本质,理解乘法的意义,为后续数域扩张后的小数乘法埋下了伏笔。】

