如何让学生理解圆周率是一个定值
文|任敏龙 郑洋
如何让学生理解圆周率是一个定值,可以采用下面的方法。
1.认识圆的周长与什么有关。
(1)画一画,让学生画大小不等的圆,指认所画圆的周长。
(2)想一想,圆的周长与什么有关?经观察比较得知:圆的周长与直径(或半径)有关,圆的周长随着直径的增大而增大、减小而减小。
2.猜想直径变化引起周长变化的规律。
(1)直径4cm和2cm的圆,写出两圆直径比,求出比值,即,猜想周长是怎样的关系?形成猜想,如:。
(2)如何验证?测量两圆周长,求比值。
3.讨论如何测得尽可能准确的圆周长。
(1)讨论得到测量圆周长的两种方法:“绕线法”和“滚动法”。

(2)评估两种方法:“滚动法”难以控制滑动,“绕线法”较为稳妥。
(3)讨论“绕线法”的要领:①起点和终点重合;②线要绕紧圆周。
(4)如果测量值差异较大:①改进方法重新测量。②在①的基础上,多测几次求平均值。
4.验证关系。
(2)用不同的圆,研究周长之比是否等于直径之比。
(3)交流研究结果。
5.认识圆周率是一个定值。
(2)验证:求多个圆周长与直径的比值,看看是否相等。求得结果大概是3倍多一些。
6.介绍“周三径一”。
约成书于公元前1世纪的我国第一部算学著作《周髀算经》中,就记载有圆“周三径一”这一结论。
7.拓展:借助演绎推理认识圆周率是定值。
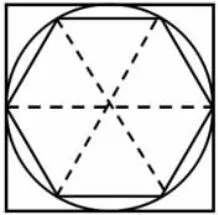
(1)呈现下图,引导学生认识:
C正六边形 (2)引导学生想象(缩放)各种大小不同的圆,总存在,3d<C圆周长<4d,更接近3d。 (3)引导思考:内接和外切正多边形边数越多,倍数的范围越小。 8.拓展:介绍“割圆术”。 魏晋期间伟大的数学家刘徽提出著名的割圆术,得出圆周率π=3.1416。南北朝时科学家、数学家祖冲之求得圆周率3.1415926<π<3.1415927,是当时最精密的圆周率,而且保持世界纪录九百多年。