短参考载波索引差分混沌移位键控通信方案

徐思远，杨 华，蒋国平

(1.南京邮电大学电子与光学工程学院、微电子学院，江苏南京 210023 2.南京邮电大学自动化学院、人工智能学院，江苏南京 210023)

随着5G通信的高速发展，信息通信进入新时期［1］。信息传输的保密性逐渐引起重视，将混沌理论与通信技术相结合，保密通信领域进入了新时期。混沌理论瞬间成为学术界关注的焦点。

混沌信号是一种有界的、非周期的、类随机信号。它对初值十分敏感，具有良好的自相关性和互相关特性。作为混沌理论在数字通信领域的典型应用，混沌数字调制本质上是一种扩频通信技术。它使用非周期的宽带混沌信号替代传统数字调制中的正弦载波，不但具有扩频通信抗干扰、抗多径衰落的特点，还具有自身高保密性、低功耗、低成本的独特优势。在过去几十年间，学术界提出了许多混沌数字调制方案［2－3］。

作为第一种混沌数字调制方案，混沌移位键控（Chaos Shift Keying，CSK）要求接收方重建与发送方严格同步的混沌基函数，这在实际的信道条件下较难实现［4－6］。 随后，差分混沌移位键控（Differential Chaos Shift Keying，DCSK）方案巧妙地绕开了混沌同步问题，将混沌参考信号和信息信号都发送给接收方，接收方通过这两种信号的相似程度来恢复信息。由于系统结构简单，DCSK系统一经提出便引起了学术界的广泛关注［7－8］。 但是，DCSK 系统也存在比特速率、能量效率偏低，宽带射频（Radio Frequency，RF）延时线在硬件上较难实现等问题。

为提高频谱效率，Galias等［9］提出了正交混沌移位键控（Quadrature Chaos Shift Keying，QCSK）系统。QCSK利用混沌信号及其希尔伯特变换作为载波，在比特误码率（Bit Error Rate，BER）性能基本保持不变的情况下将系统的传输速率提高了一倍。Xu等［10］提出了码移差分混沌移位键控（Code-Shifted Differential Chaos Shift Keying，CS-DCSK）系统，用Walsh码来分开混沌参考信号和混沌信息信号，有效地避开了RF延时线的问题。考虑到Walsh码数量有限，Kaddoum等［11］提出了高速率差分混沌移位键控（High Data Rate Differential Chaos Shift Keying，HCS-DCSK）系统，利用混沌信号加权保证各路数据信号的独立性，通过所有信息比特共享相同的参考信号实现较高的传输速率。为进一步在发射机中避免RF延时线问题，Kaddoum等［12］又提出了多载波差分混沌移位键控（Multi-Carrier Differential Chaos Shift Keying，MC-DCSK）技术。与上述方案中时分多址和码分多址的方式不同，MC-DCSK将参考信号和信息信号在频域上分开，将多载波技术与DCSK相结合，在不同的载波上并行传输多路数据比特。与DCSK相比，这种方案在传输速率和能量效率方面都有了较大的提升，BER性能也得到了改善［13－14］。 同时，Kaddoum 等［15］对参考混沌序列进行压缩，提出了短参考差分混沌移位键控（Short Reference Differential Chaos Shift Keying，SR-DCSK）系统，通过缩短参考混沌序列的长度来提高比特传输速率与能量效率。

近年来，使用传输实体的索引值来传输数据信息的索引调制（Index Modulation，IM）技术逐渐与混沌数字调制技术相结合。码索引差分混沌移位键控（Code Index Modulation DifferentialChaosShift Keying，CIM-DCSK）方案将码索引调制应用于DCSK，利用一组Walsh码的索引值来传输数据信息［16］。置换索引差分混沌移位键控（Permutation Index Differential Chaos Shift Keying，PI-DCSK）方案利用许多预定义置换操作的编号来携带更多数据比特［17］。载波索引差分混沌移位键控（Carrier Index Differential Chaos Shift Keying，CI-DCSK）方案借助被激活子载波的索引值来传递数据信息，既可以节省发射功率又可以提高系统的比特传输速率［18］。遗憾的是，CI-DCSK系统传输的混沌参考信号并未携带任何数据信息，导致其在能量效率和比特误码性能等方面的表现并不十分理想。

本文提出一种短参考载波索引差分混沌移位键控（Short Reference Carrier-Index Differential Chaos Shift Keying，SR-CI-DCSK）调制方案。新系统通过缩短发送的混沌信号长度来提升CI-DCSK系统的能量效率；借助对混沌信号的多次复制操作，在信息信号中引入一定的重复性；利用信息信号的重复性，采取分段取平均的方式降低信息信号中的噪声，达到改善系统BER性能的目的。

1 系统模型

1.1 SR-CI-DCSK 发射端

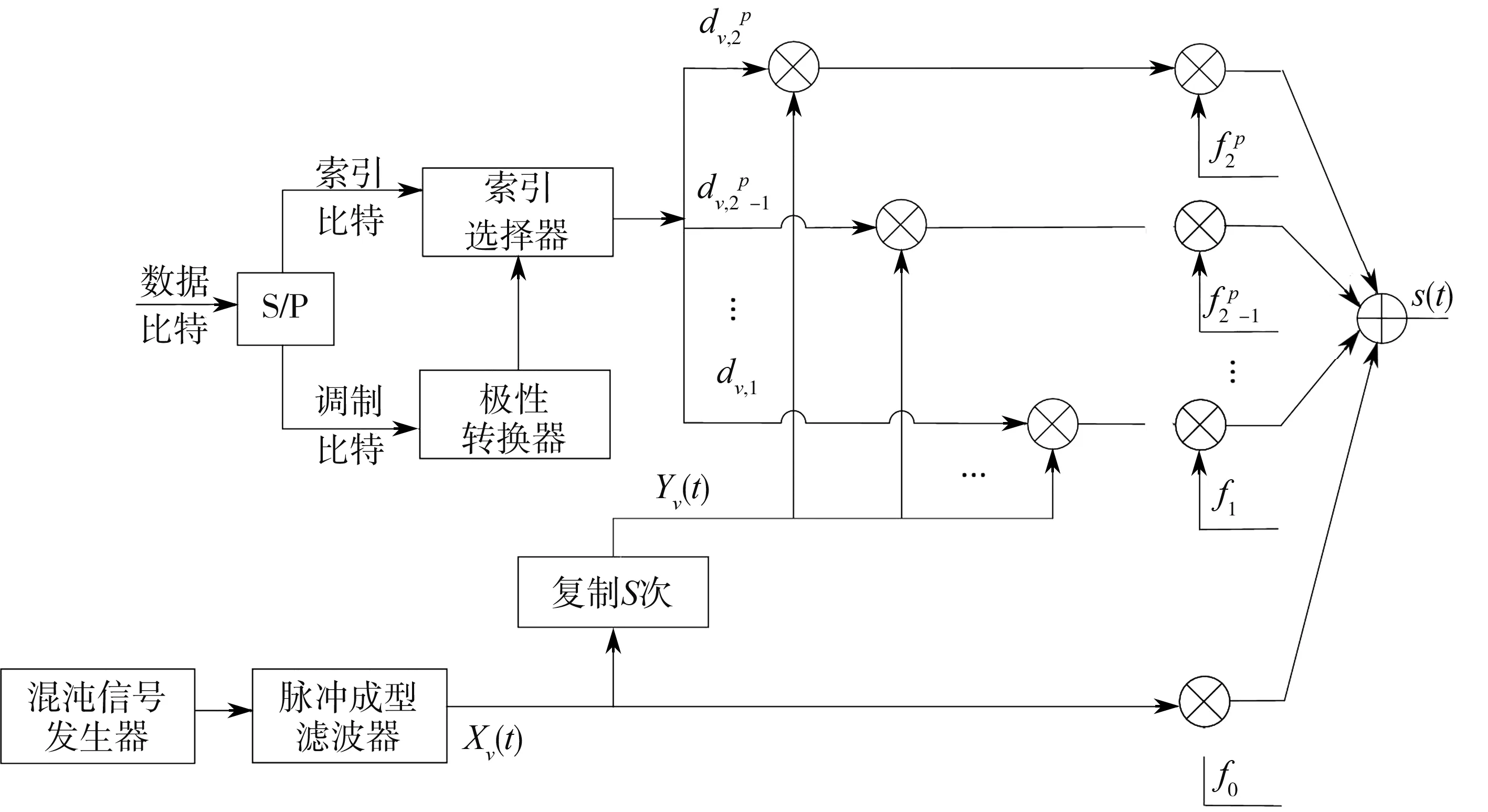
图1 发射端原理框图

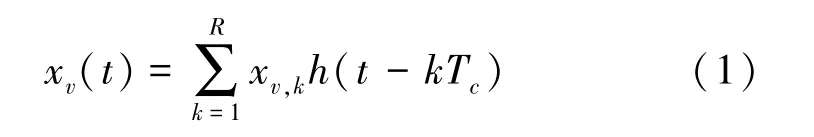
其中，Tc为码片时间，xv，k为混沌信号发生器在第v个符号持续时间内生成的第k个混沌样本，h（t）为具有归一化能量的脉冲成型滤波器的时域冲击响应。

将 xv（t） 复制 S 次，生成重复混沌信号 yv（t），作为当前符号周期内的信息载体

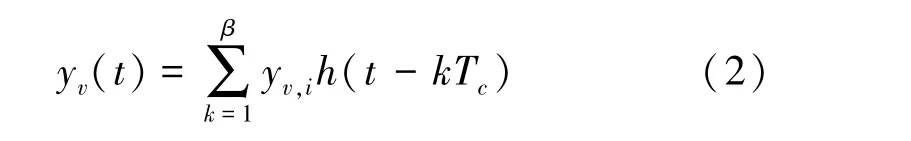
其中

SR-CI-DCSK系统中可用子载波总数为2p＋1。 其中，中心频率为f0的子载波为参考载波，用于发送混沌参考信号；剩余的2p个子载波为数据载波，并从1到2p进行索引标记。在第v个符号周期内，系统传输 p＋1 位数据比特，即 Sv＝ ［av，1，…，av，p＋1］。 其中，av，1，…，av，p为索引比特，av，p＋1为调制比特。 首先，调制比特 av，p＋1∈｛0，1｝ 通过极性变换转变为极性调制比特 bv，p＋1∈｛ － 1，1｝；与此同时，索引选择器根据当前索引比特，从2p个数据载波中选择1个子载波进行激活（被激活的子载波被称为有效载波，剩余的数据载波被记为无效载波）。最后，极性调制比特将以DCSK的方式被调制在yv（t）上并经由有效载波传送出去。

为了从2p个数据载波中选出当前符号周期内的有效载波，索引选择器会将当前输入的p个索引比特映射为2p个载波系数。图中，dv，m表示在第v个符号持续时间内第m个数据载波对应的载波系数。在这些系数中，只有有效载波对应的载波系数等于极性调制比特，所有无效载波对应的载波系数均为零。图中的索引选择器可以使用不同的映射规则生成载波系数，本文使用自然二进编码的方法来映射。以p＝ 2为例，当索引比特 av，1av，2＝ 10 时， 生成的载波系数dv，1…dv，4＝ 0010， 即选中索引为 3 的数据载波作为传输信息信号的有效载波。

(1)分类职称评审模式。以广西职称评审权下放到具体高校为契机，根据学院的办学定位，结合各学科、岗位特点，建立分类、分层次的评审机制，用“教学和科研并重”的分类评价模式取代传统的“重科研、轻教学”的评价，同时将教师的创新创业实践及成果纳入评价体系。如教师指导学生在国家级学科竞赛获得特等奖、一等奖的视同发表一篇中文核心，激发教师的创新创业活力。

SR-CI-DCSK发射机在第v个符号持续时间内发送信号的表达式为

其中，φm和fm分别表示第m个子载波的相位角和中心频率。

1.2 SR-CI-DCSK 接收端

SR-CI-DCSK系统的接收机如图2所示。接收信号首先分别与2p＋1个相应频率的同步正弦载波相乘。经过匹配滤波器滤波后，乘积信号会在每个kTc时刻被采样。然后，将采样后的离散信号储存在两个矩阵中，即，混沌参考信号存储在矩阵A1×R中，而信息信号存储在矩阵中；将矩阵中的每一行分成S段，对每一段的元素进行标记，所有标号相同的元素相加并取平均，得到新的行向量，所有的行向量按原有的顺序排列，得到新的矩阵； 最后，将 Zv＝ A ×的结果输入检测器检测。相关矩阵 Zv的计算方式如下

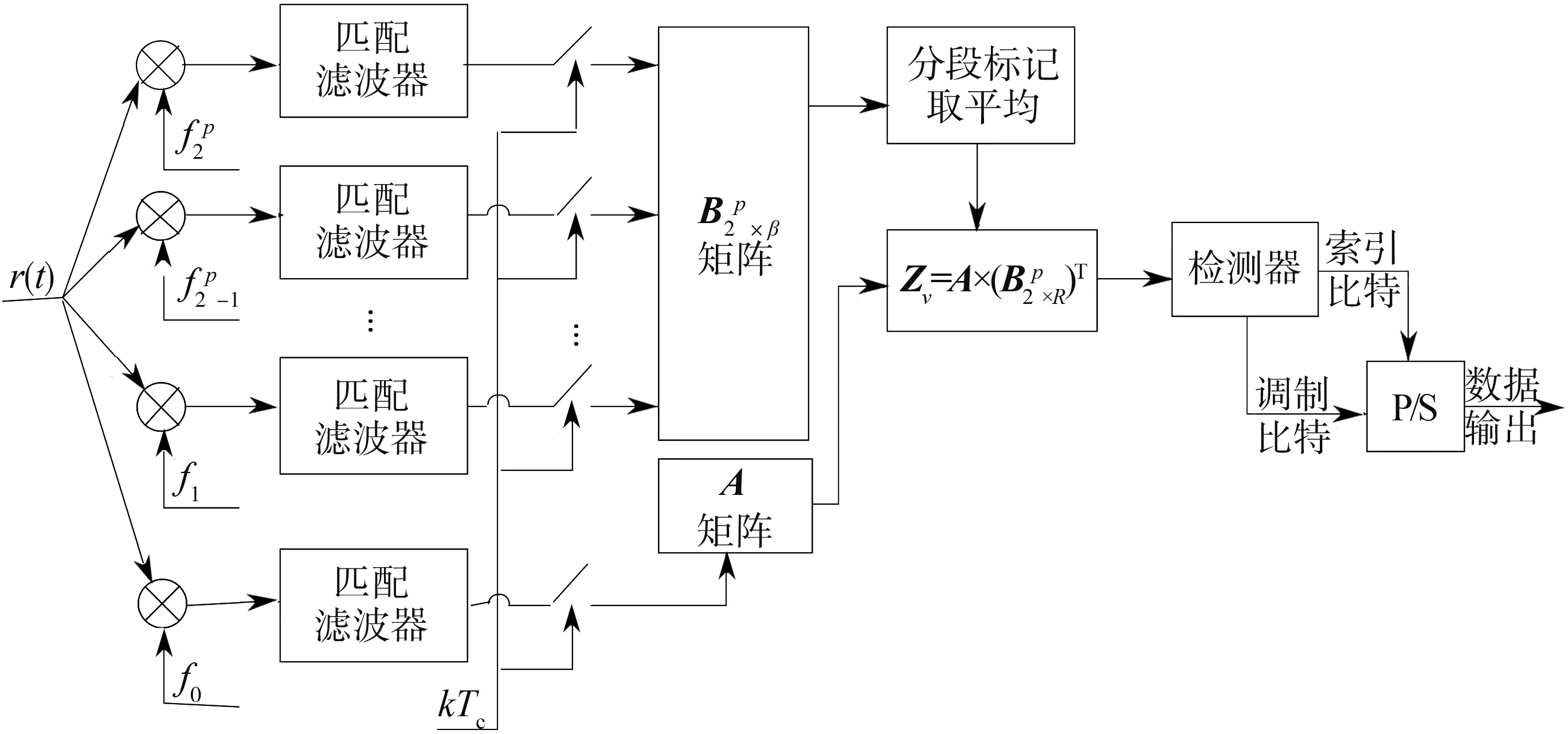
图2 接收端原理框图

图2中使用基于最大能量的检测器恢复索引比特。首先，计算矩阵Zv中每个元素的绝对值，找到其中的最大值；然后再根据最大值所在载波的索引，恢复出长度为p索引比特。恢复出的有效载波的索引可以表示为

其中，表示第v个符号持续时间内有效载波的索引估计值。

最后，根据Zv中具有最大绝对值的元素的极性符号来恢复出调制比特。具体规则如下

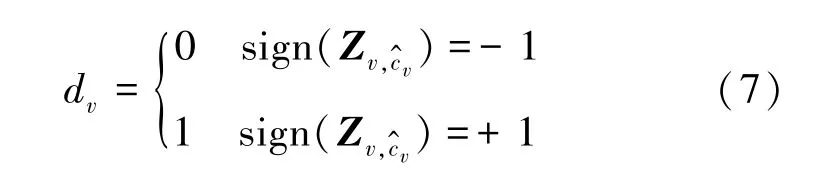
其中，dv表示恢复出的第v个符号持续时间内发送的调制比特。

2 BER性能分析

考虑在无线通信中常用的信道模型——由L个独立同分布的瑞利慢衰落路径构成的多径衰落信道［9，18－19］。 该模型为

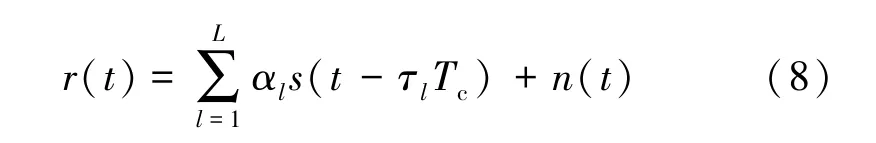
其中，s（t）为输入信号，r（t）为经过信道后的接收信号，αl和τl为第l条路径的传播增益和码片延迟，n（t）为加性高斯白噪声，其功率谱密度为N0／2。若αl＝1，τl＝0，上述信道则退化为AWGN信道。

为了便于分析，假设在第v个符号周期内的有效载波为第1个数据子载波。考虑到符号持续时间比最大多径延迟大得多，即0＜τlmax≪β，此时可以忽略符号间干扰（ISI）［18］。假设所有的子载波是完全同步的，矩阵Zv的第m个元素可表示为

在解调索引比特的过程中，只要有一个无效载波对应的相关值的绝对值大于有效载波对应的相关值的绝对值，索引比特的解调就会发生错误。因此，可以获得当前索引符号解调正确的概率为

其 中， f｜Zv，1｜（r） 表 示 ｜Zv，1｜的 概 率 密 度 函 数（Probability Density Function， PDF）， F｜Zv，m｜（r） 表示｜Zv，m｜的累计分布函数（Cumulative Distribution Function， CDF）， 1 ＜ i≤ 2p。 根据文献［20］， Zv，m服从均值为式（11）和方差为式（12）的高斯分布，则F｜Zv，m｜（r） 和 f｜Zv，1｜（r） 可以分别表示为

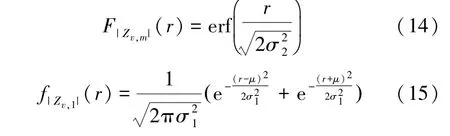
其中，erf（·）表示误差函数，将式（14）和（15）代入式（13）中，则式（13）可以写成

只考虑传播增益α1＝1且码片延迟τ1＝0的第一条路径，式（21）还可以用来计算AWGN信道中SR-CI-DCSK系统的BER。

3 能量效率分析

在SR-CI-DCSK系统中若每个符号发送的比特数为p＋1，当前符号周期内参考信号长度为R、信息信号长度为β，则发射信号的符号能量可以计算为

其中，Edata表示每个符号的数据能量，Eref表示每个符号的参考能量，可以计算出数据信号和参考信号的能量为

根据文献［12］可以推导出，在相同条件下CIDCSK系统的DBR为（p＋1）／2。

图3给出了SR-CI-DCSK与CI-DCSK系统的DBR性能对比，从图3可以看出，SR-CI-DCSK系统的DBR性能优于CI-DCSK系统，即与CI-DCSK系统相比，SR-CI-DCSK系统具有较高的能量效率。

图3 p＝4，β＝100，SR-CI-DCSK、CI-DCSK 系统的DBR性能对比

4 仿真结果与分析

本节在不同信道条件下对SR-CI-DCSK系统、CI-DCSK系统和DCSK系统分别进行MonteCarlo仿真，验证第2节中理论分析的正确性，讨论系统参数（如：参考信号长度R，索引比特个数p等）对SR-CIDCSK系统BER性能的影响，并完成不同系统的BER性能比较。本节仿真中使用的三径瑞利衰落信道模型参数分别为τ1＝ 0，τ1＝ 1，τ1＝ 2。

4.1 理论与仿真性能对照

图4给出了在AWGN信道中SR-CI-DCSK系统的BER性能与参考信号长度R之间的关系。图中，信息信号长度β＝100，当参考信号长度R也等于100时，此时SR-CI-DCSK系统等价于CI-DCSK系统。很明显，图中的理论值和仿真结果都非常吻合，这证实了第2节理论分析的准确性。

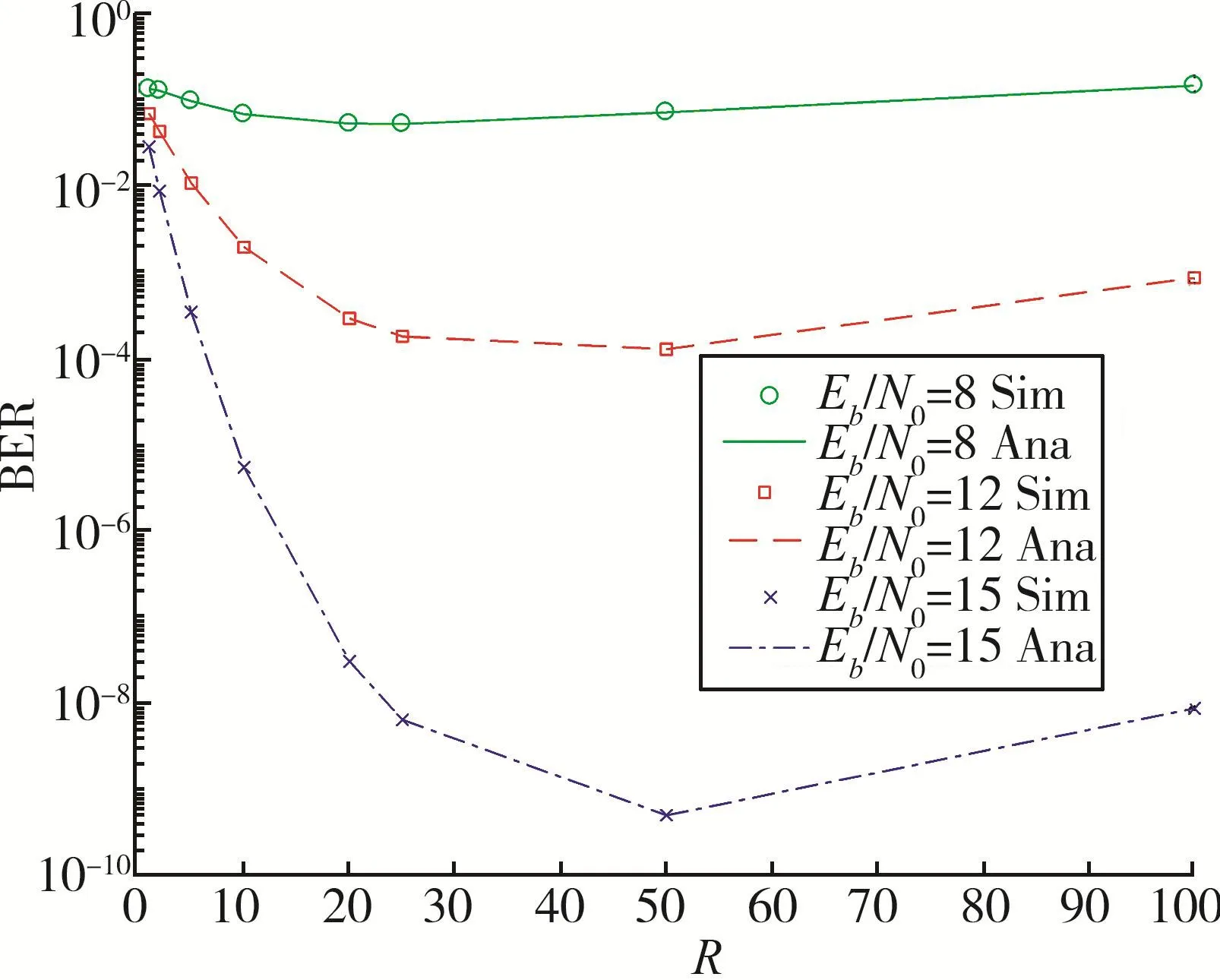
图4 p＝4，β＝100，AWGN 信道下 SR-CIDCSK系统的BER性能与R的关系

图4中还可以看出，随着R的增大，系统的BER性能逐渐变好，达到最佳值后BER性能有所下降。BER的变化曲线有波谷现象，即存在最佳R值使得在该信噪比条件下，系统的BER性能达到最优。可以清楚地观察到，在大信噪比条件下（Eb／N0＞12），当R为50时，SR-CI-DCSK系统的BER性能达到最优。该结论在图5中也得到了验证。

图5 p＝4，β＝100，R＝5，10，20，50，AWGN 信道下SR-CI-DCSK系统的BER性能与信噪比的关系

图6分别在AWGN和多径瑞利衰落信道中给出了p对SR-CI-DCSK系统BER性能的影响。可以看出，当p增加时，所提出的系统的BER性能表现更好。

图6 R＝50，β＝100，SR-CI-DCSK 系统的仿真和理论BER性能对比

4.2 不同系统BER性能对比

图7分别在AWGN和三径瑞利衰落信道中比较了SR-CI-DCSK系统、CI-DCSK系统和DCSK系统的BER性能。图7中，SR-CI-DCSK系统参考信号长度R设置为50，SR-CI-DCSK和CI-DCSK系统的p设置为4、混沌序列长度β设置为100。从图7中可以明显看出，在两种信道中，SR-CI-DCSK系统的BER性能都优于CI-DCSK和DCSK系统。

图7 在AWGN和三径瑞利衰落信道上CI-DCSK、DCSK、SR-CI-DCSK系统的性能比较

5 结束语

本文提出了一种新的SR-CI-DCSK调制解调方案。该方案利用缩短参考信号的方法，有效地降低了CI-DCSK系统中的噪声干扰，明显地改善了系统的BER性能。理论分析和仿真结果表明：与CIDCSK系统相比，SR-CI-DCSK系统在AWGN信道和多径瑞利衰落信道中都具有更高的能量效率和更好的BER性能，应用前景广阔。