基于差分隐私的群智频谱感知算法

胡 敏，朱 琦

(南京邮电大学江苏省无线通信重点实验室，江苏南京 210003)

无线通信技术的飞速发展引起无线设备剧增，使得无线频谱资源十分稀缺。目前频谱资源采用固定的分配方式进行授权，因此频谱利用效率很低，且极度不平衡，认知无线电系统应运而生。认知无线电可以感知系统环境，寻找空闲的频谱，并进行动态的频谱分配，这样可以有效地提高频谱利用效率。认知无线电的关键技术是频谱感知。文献［1］提到在认知无线电网络中，频谱共享的最重要目标是使买卖双方都受益，为了增加频谱共享中产生的总收益，文献［1］介绍了频谱代理与多主服务提供商之间的存储机制，并提出了基于该机制的频谱交易算法。多用户协作频谱感知可以解决单用户感知受阴影效用、深度衰落等影响的问题，为了激励更多用户参与频谱感知，将群智感知的激励机制与频谱感知结合很有必要。文献［2］考虑到次用户自愿参与感知任务与实际情况不符合，提出了不仅利用群智感知提供足够的次用户，并且配备频谱传感器，将想参与感知任务之间的互动建模为合作博弈，通过理论证明了该博弈是一个NP-hard问题，且存在一个均衡解，次用户可以通过调整自己的感知时间使得感知效用最大，也可以尽量减少平台的成本，通过使用一种改进的差分算法证明了此模型的优越性。文献［3］考虑到可能存在部分用户不愿参与感知从而破坏协作频谱感知，提出了一种基于社会效用的激励机制来解决自私问题，该机制将个人的利益转化为以社会的利益为中心，也就是说次用户在一定的激励下会选择和自己联系紧密的次用户共享信息，从而完成协作感知。文献［4］重视激励次用户协作感知，研究了一种基于信誉的CSS激励框架，该激励框架将协作频谱感知建模为间接互惠博弈。在该博弈中，次用户根据自己能获取的有效信道数量选择性地向融合中心报告感知结果，通过推导求解该博弈模型证明了此激励机制可以提升融合中心的判决精度。文献［5］提出了一种基于贝叶斯博弈的协作频谱感知算法，所有参与感知任务的次用户都能根据贝叶斯博弈选择使得各自效用最优的策略，该算法可以提高检测概率，提升系统性能。

近年来保护用户隐私逐渐被人重视，文献［6］提出了一种在不损害MCS用户隐私的情况下的机制，该机制可以保证群智感知数据的质量，通过实验证明该机制在提升数据质量和消除MCS用户动机方面有较大作用。文献［7］提出了一种用于移动群智感知的个性化隐私保护任务分配框架，该框架可以有效地分配任务，同时提供个性化的位置隐私保护。具体做法是将各个用户到任务的模糊距离上传至服务器，从而起到保护用户的作用；文献［7］还提出了一种概率优胜者选择机制（PWSM），通过将任务分配给最大概率与自己距离最近的用户来减少行程；此外文献［7］提出了一种VPDM付款机制，通过考虑其移动成本和隐私级别来确定付给获胜者的报酬。文献［8］以实现最小社会成本为目标提出了两个保护隐私的激励机制，在前者中，每个用户都针对其愿意执行的一组任务提交投标；在后者中，每个用户都为其任务集中的每个任务提交出价。文献［8］中提出的两种框架均基于平台定义的评分功能选择用户，并提出了线性函数和对数函数两个得分函数以实现这两个框架。文献［7］考虑到在保证最优分配任务情况下用户具体位置暴露的问题，提出了一种用于群智感知技术的数据发布机制，使用基于用户密度并考虑用户分布不均的方法，证明了该机制满足差异性隐私，且为用户的位置提供了严格的保护。此外，文献［9］还提出了一种基于地理广播的区域选择方法，此方法可以平衡任务分配的成功率和平台的花费。已有的保护隐私的文献一般都没有结合频谱感知的场景。

在研究频谱感知相关文献中，较少考虑用户的隐私问题，因此本文主要解决在频谱感知场景下的用户隐私保护问题，具体方法是将保护隐私的激励机制与协作频谱感知结合起来，提出一种具有隐私保护的基于拍卖的频谱感知算法，并引入了差分隐私的概念，将指数机制应用于平台与用户间的反向拍卖。平台选择获胜用户时将用户的信誉值考虑在内，并且使用了一种基于指数机制的线性得分函数选择最优的用户集。

1 系统模型

本文的系统模型如图1所示，平台发布频谱感知任务，次用户根据发布的任务对频谱进行感知。假设存在1个主用户，次用户数为N，SU＝｛su1，su2，su3，…，suN｝， 各个次用户均可以通过能量检测感知主用户频段，得到相应的检测结果和检测概率Pdi。 假设各个次用户均愿意参与感知任务的拍卖过程，次用户将感知结果以及对任务的报价bi（报价范围是 ［bmin，bmax］）发送至平台，平台根据一定的准则选择一定数量的次用户完成感知任务，接着平台发放相应的报酬pi给被选中的用户。假设被选中的次用户集为W，各个次用户的感知花费为ci，则用户i∈SU的效用ui为

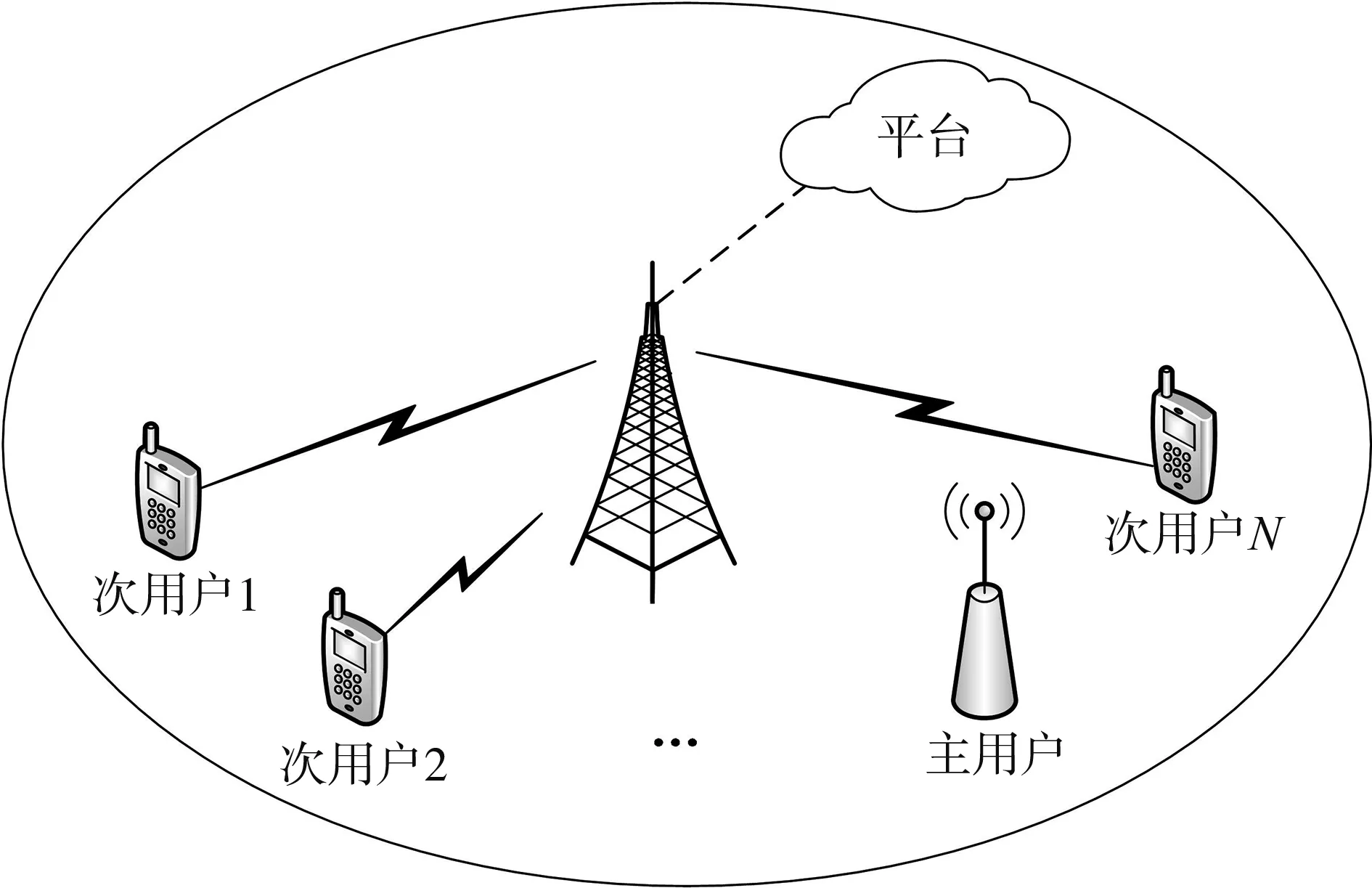
图1 系统模型图

现有文献中平台一般会公布获选的用户以及对应的报价，假设用户A在前k轮竞价中均获胜，则他的报价信息被泄露，潜在的用户可以通过研究分析其前几轮的报价，通过恶意降低自身报价被平台选中，如果有数量足够多的潜在用户采取类似的方法，即使将用户的信誉值考虑在内，平台最终选取的用户集不是最优的，甚至会造成错误的感知结果。因此本文考虑用户的隐私，将用户的报价bi作为需要保护的信息，涉及到隐私的相关定义如下：

定义1：（ε差分隐私［10］）M 为一个随机函数，如果两个输入集A和B只相差一个单位，若对于任意的结果集 O ∈ Range（M）， 满足 Ps［M（A） ∈O］≤exp（ε） ×Ps［M（B）∈O］，则该函数是ε差分隐私的。

在本文中，随机函数 M对应优化的策略，Range（M）为优化策略的结果空间集。关于差分隐私的一种衍生如定义2所示。

定义2：（近似差分隐私［11］）M 为一个随机函数，对于只相差一个单位的输入集合A和B，若任意的结果集 O ∈ Range（M），满足Ps［M（A）∈ O］≤exp（ε） × Ps［M（B） ∈ O］ ＋ δ，则该函数是 （ε，δ）差分隐私的。

此外，一般拍卖机制的真实性是由定理1所保证的。

定理1：假设Pri（z）表示当次用户报价为z时被平台选中的概率。对于报价向量b（b＝（b1，b2，…，bn）） 和报酬向量p（p ＝（p1，p2，…，pn）） 的激励机制满足真实性，当且仅当任意的次用户满足以下3个条件［12］：

在现有的差分隐私的文献中，指数机制常常被用于设计提供差分隐私保护的激励机制［6］。指数机制的关键是其得分函数，用f（A，o）表示，该得分函数将输入的数据集A和结果o∈O映射为一个真实价值的得分。这个得分表示所得结果的好坏。指数机制（A）选中结果o∈O的概率可以表示为

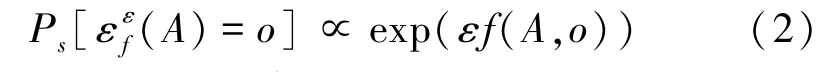
其中ε为一个很小的常量。

假设Λ代表两个输入集之间差异的上限，那么指数机制有如下性质：

假设平台的预算为B，且平台采用表决融合对用户集上报的数据进行数据融合，则表决融合后的检测概率 Pd为［14］

其中，ui表示次用户的判定结果。

2 基于差分隐私的频谱感知反向拍卖算法

建立一个平台与次用户之间的反向拍卖模型，平台购买用户的感知数据，用户竞价出售感知数据获得收益。平台根据一定的准则选择合适的用户集完成感知任务，次用户的信誉值ri是其中一个重要参数，假设次用户的信誉值仅与最近的前k轮的任务参与度相关，则有

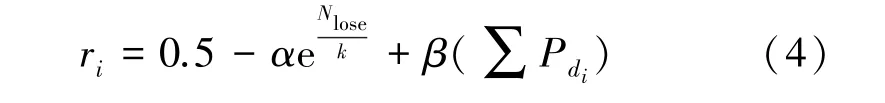
其中，Nlose表示最近k轮感知任务中未被选中的次数，α、β为加权因子，且Pdi可以表示为

其中，Pf表示虚警概率，即当主用户没有占用频谱时次用户误判主用户占用频谱的概率，ti为用户i的感知时间，fs为采样频率，一般为定值，tifs则是采样点数，SNRi表示次用户接收主用户发送信号的信噪比，Q函数表达式为

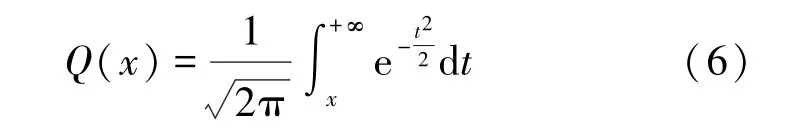
本文的优化目标是检测概率最大化，优化的策略为选择的用户集，同时考虑到隐私保护，优化目标为

该激励机制目标为获得最大检测概率，是一个NP-hard问题，通过分析系统模型以及对理解差分隐私相关定理，本文将指数机制和反向拍卖结合起来，设计一个可以保证计算有效性、个人理性、真实性以及近似最大检测概率。

在设计的机制中，所有的用户向平台上报自身对任务的报价，平台会根据用户的信誉值以及报价计算各个用户被选中的概率，在预算范围内，平台根据概率从大到小的顺序选择获胜的用户，被选中的用户执行任务并上报感知结果，平台向选中的用户支付一定的报酬，同时所有用户更新自身的信誉值以参与下一轮的感知任务。该机制具体分为用户参与、选择获胜者、支付报酬几个阶段，具体如下：

（1）用户参与

平台发布感知任务，所有的次用户积极参与任务，用户向平台提交自己的报价bi，等待平台选择。同时平台能看到每个参与用户的信誉值情况。

（2）选择获胜者

设计的激励机制会给每个参与任务的次用户分配一个概率值，该概率值代表每个用户被选中的概率，信誉值是其中的一个重要参数，表示参与的次用户提供信息的质量，其表达式如式（2）所示。此外，为了应用指数机制解决隐私问题，本文设计了满足单调非递增性质的得分函数，具体为线性得分函数：flin（x）＝x。 每轮竞选中，对于竞选者i∈SU，其被选中的概率为

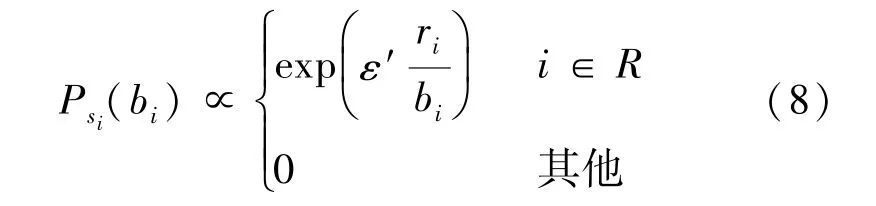
其中 ε′＝ ε／（εln（e／δ）Λ）。 为了保证得分函数非负，将概率进行归一化，则其表达式为

平台根据设计的得分函数计算每个用户获胜的概率大小，在预算固定的情况下根据概率从大到小选择用户。此时无论用户是否被选中，用户都会更新此刻的信誉值。被选中的用户得到任务的执行权，完成感知任务并上报感知数据给平台，平台负责之后的数据处理，得到近似最大检测概率。

（3）支付报酬

根据定理1，对于任意获胜者i，其报酬pi可以表示为

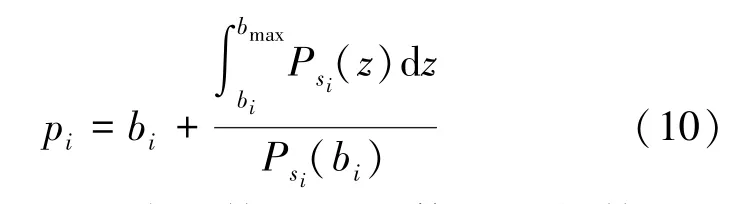
所提基于差分隐私算法的具体步骤如算法1所示。

算法1 差分隐私的频谱感知反向拍卖算法

3 激励机制性质证明

本文提出的算法需要同时满足以下几个重要的性质：

（1）计算有限性。如果设计的机制能在多项式时间内结束，则在计算上是有效的。

（2）个人理性。如果每一个用户参与任务都能获得非负效用，则该机制具有个人理性，即所有次用户i∈W，当用户未虚假报价时，其效用ui≥0。

（3）真实性。如果用户对任务的报价等于其真实价值时，其效用达到最大，则该机制满足真实性。

（4）检测概率最大化。该机制在预算范围内，获得最大检测概率。

定理4：线性得分函数可以保证计算有效性、个人理性、真实性，并且可以实现 （rmaxε（e － 1）／e，δ）差分隐私。

（1）计算有效性证明：由于用户数N有限，算法1最多执行N次，因此算法的复杂度为O（n），其计算有效性得证。

（3） 真实性证明：由式（8）和（9）可知，用户 i被选中的概率函数Psi（bi）是关于bi的单调非增函数，此外，在本文模型中所有参与的用户报价都不高于bmax，

证明：假设β和β′是两个只相差一个用户报价的输入集，用 M（β）和 M（β′）分别代表输入 β和β′线性得分函数选择的用户集。可以证明对于任意长度为 l的用户序列 S＝i1，i2，…，il，即使对外公布用户被选择的顺序，线性得分函数也可以保证差分隐私。对于给出的两个输入集β和β′，可以得到其概率比为

4 仿真结果与分析

采用MATLAB对算法进行仿真，仿真场景如图1所示，主用户随机分布在区域内，N个次用户随机分布在半径1 km的区域内，次用户的报价均匀分布在1～10，预算默认值为100，差分隐私参数默认值ε ＝ 0.1，δ＝ 0.25。

为了验证提出的算法性能，本文与文献［16］中基于位置的真实拍卖场景和文献［17］进行对比，文献［16］没有考虑用户的隐私问题，文献［17］考虑了隐私问题，但是目标为最小化报酬。给定一个机制M，假设β和β′是两个只相差一个用户报价的输入集，用M（β）和M（β′）分别代表输入β和β′得到的结果。用PL表示隐私泄露，PL的值越小表明区别两个结合越难，因此隐私保护越好，PL定义为

图2给出了隐私泄露随着用户数变化的曲线，由于文献［16］不考虑隐私泄露问题，因此其隐私泄露无穷大，从图中可以看到，文献［17］中提出的DP-hSRC算法也能一定程度上保护隐私，本文算法一定程度上保护了隐私且隐私泄露随着用户数的增加而减小，这是因为用户数增多，区分相差一个报价的输入集得到的结果会更困难，隐私保护越好。文献［17］提出的机制是单价机制，其中一个用户改变价格都会极大改变机制的结果，从而PL值会增加，因此隐私泄露高于本文算法。

图2 隐私泄露随用户数变化曲线

图3给出了系统的检测概率随用户数增加的变化趋势，图3显示用户数越多，检测概率越高，这是因为当用户数增加时，平台可以选择更多更优次用户感知任务，从而提高检测概率。文献［16］中由于没有考虑用户的隐私保护，因此有部分用户不愿意参与感知，因此检测概率低于本文算法。文献［17］虽然考虑了用户隐私，但目标为最小化平台花费，因此检测概率低于本文算法。

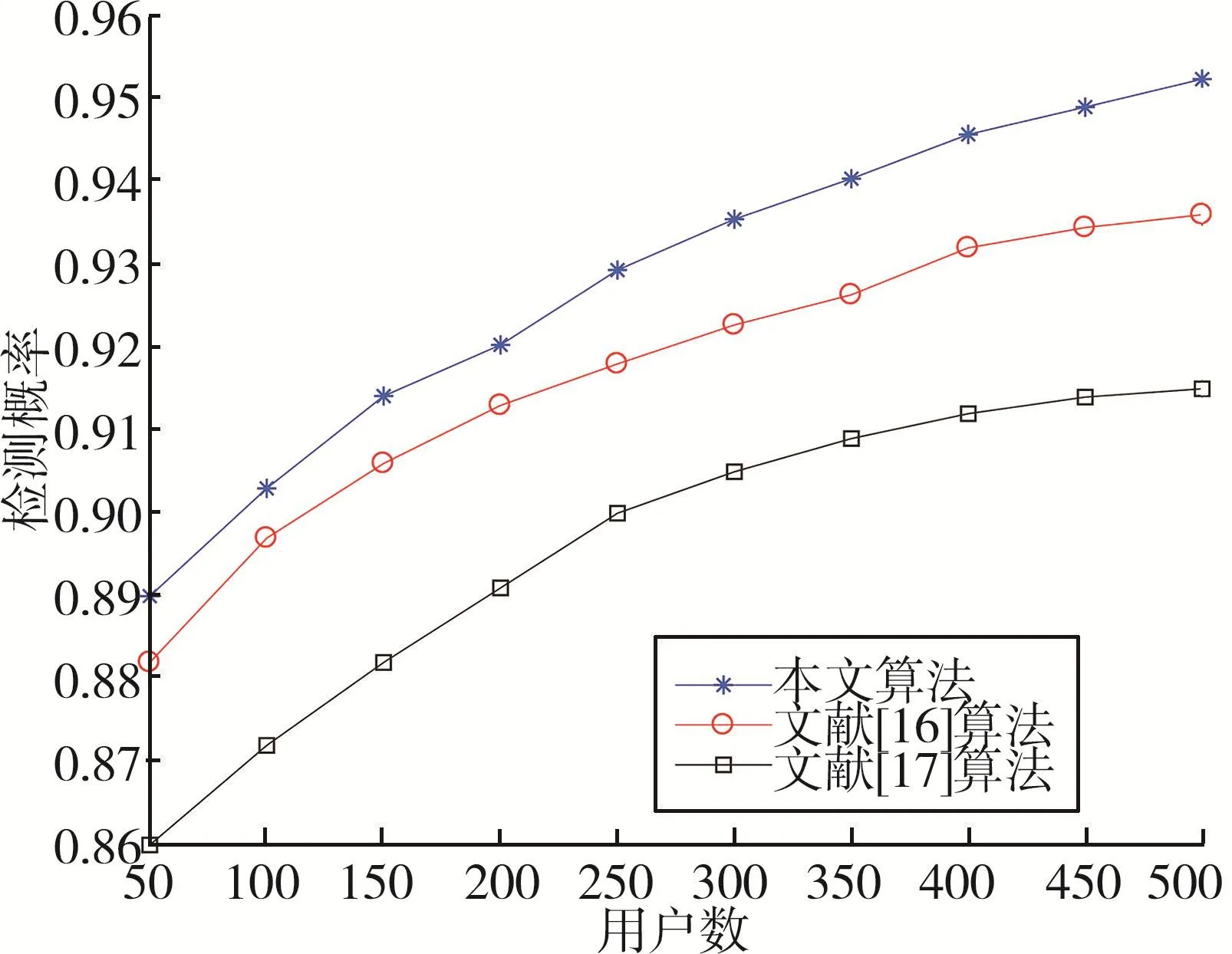
图3 检测概率随用户数变化曲线

图4给出了差分隐私参数ε的变化对隐私泄露的影响，此时固定用户数为150，预算为100，从图中可以看到隐私泄露程度随着ε的增大而小幅度增大，同时可以看到本文算法优于对比算法。

图4 隐私泄露随ε变化曲线

图5给出了隐私泄露随着预算变化的曲线，从仿真可以看到预算增大，隐私泄露减少，这是因为当预算增加时，平台可以选择更多次用户，参与感知的用户越多越难区分平台选择的用户集，从而保护用户的隐私情况。

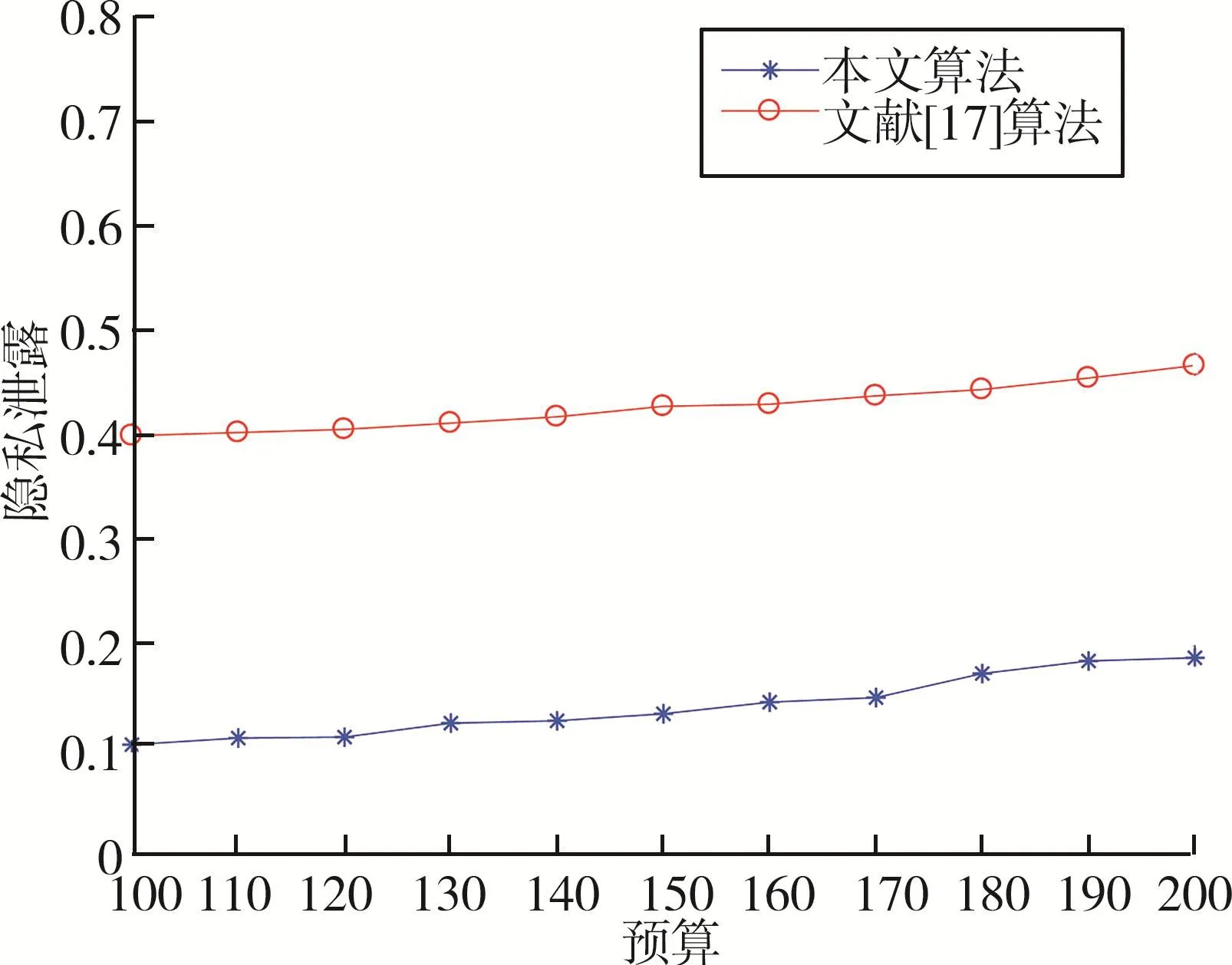
图5 隐私泄露率随预算变化曲线

图6给出了检测概率随着预算变化的曲线，从图中可以看出检测概率随着预算的增加而增大，这是因为当预算增加时，系统可以招募更多的用户参与感知任务，因此可以有更多的用户帮助判决最终的频谱结果，从而得到更准确的检测结果。从图中可以看到文献［16］中算法得到的检测概率高于本文算法，这是因为文献［16］没有考虑用户的隐私问题，假设所有用户均自愿参与感知任务，因此可以选择最优的次用户集，从而提升系统的检测性能。

图6 检测概率随预算变化曲线

5 结束语

在研究的频谱感知算法中考虑了用户的隐私保护问题，由于暴露用户报价和平台公布竞选结果可能导致任务无效以及用户的巨大损失，本文将用户的报价作为隐私内容，提出了一种具有隐私保护的频谱感知反向拍卖算法，此外设计了一种基于指数机制的差分隐私方法，将指数机制应用于线性得分函数，平台根据此得分函数选择最优的用户集，从而完成平台与用户间的反向拍卖过程。得分函数同时包含了用户的信誉值，该信誉值一定程度上反映了用户感知数据的质量，使得该机制能在一定约束下获得最大检测概率。通过仿真评估了该激励机制的一些性能，仿真结果表明提出的激励机制在能够保护用户隐私的前提下，实现近似最大检测概率。