车辆冲击荷载作用下桥梁振动响应分析

王亚东，石兴娜

（1.中交机场勘察设计院有限公司，广州 510230；2.广州华夏职业学院建筑与艺术传媒学院，广州 510935）

在车辆冲击荷载和自然环境长期共同作用下，桥梁结构都不同程度地存在结构性缺陷、损伤和功能性失效。为确保桥梁结构安全和正常使用，需定期对桥梁结构进行检测。静载试验是桥梁检测的主要方法，其测试理论与技术较为成熟，但测试成本较高，且在交通要道或特殊地形条件下难以实施[1-4]。近年来，桥梁动态测试方法因其方便快捷的优势，备受广大工程技术人员青睐，但动载检测方法仍存在一定局限性，在精度方面存在一定不足[5]。如何提高移动汽车荷载作用下桥梁挠度、应力、应变等试验精度是桥梁动态测试研究的目标。冲击系数是连接桥梁静载试验与动载试验的中间纽带，也是解决桥梁快速检测的关键。

影响桥梁冲击系数的因素包括：车辆行驶速度、路面平整度、桥梁刚度等，其中路面平整度最为复杂。首先，路面平整度引起的汽车荷载对桥梁的动态冲击不容忽视；其次，路面平整度具有随机性和不确定性，准确描述路面平整度非常困难。为此，提出采用枕木跳车测试方法来压制路面平整度影响的测试方法，即跳车条件下的动载冲击系数不再受路面平整度影响。

首先，基于车-桥耦合振动理论利用数值计算方法求解耦合振动方程，对车辆行驶速度、路面平整度等影响桥梁冲击系数的主要因素进行研究；其次，进一步分析枕木跳车条件下的车-桥系统耦合振动问题。研究结果表明：枕木跳车测试方法能有效压制路面平整度对桥梁冲击系数的影响，避免了定量描述路面平整度的困难，为桥梁快速动态测试奠定基础。

1 车-桥耦合系统简化模型及相关理论

车-桥耦合振动是一种强迫振动问题，先后经历了5 个研究阶段[6]。其中，1954年Biggs 提出利用匀速移动单自由度弹簧-质量系统分析简支梁动力响应问题的理论模型。基于该理论模型，并引入路面平整度条件，可用于分析路面平整度对车-桥耦合系统的影响。

1.1 车-桥耦合系统计算理论

根据达朗贝尔原理建立简支梁、弹簧-质量系统的动力学平衡方程如下

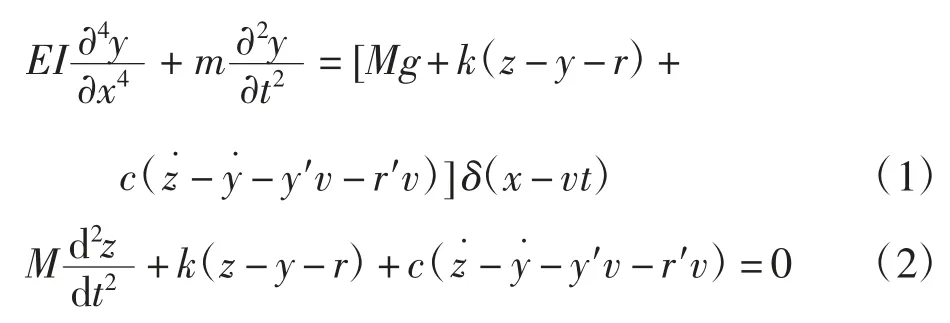
式中：E 为简支梁弹性模量；I 为抗弯惯性矩；y 为关于时间和位置的挠度函数；y˙和y′分别为关于时间和位置的一阶导数；m 为简支梁单位长度的质量；M 为车辆质量；g 为重力加速度；z 为车辆质量相对于平衡位置的位移；r 为路面平整度值；k 为弹簧刚度；c 为弹簧阻尼；v 为弹簧质量系统（车辆）水平方向的行驶速度；t 为时间；δ 为狄拉克函数。

采用数值计算方法求解振动微分方程[7-11]。根据模态叠加原理，桥梁振动位移可表示为振型的级数形式，即

式中：φn（x）是与x 相关的三角函数；qn（t）是与时间t相关的位移函数；L 为简支梁长度。将式（3）和式（4）代入式（1）和式（2）并利用模态函数正交性对式（1）积分，同时引入边界条件：简支梁两端位移为0、弯矩为0。式（1）和式（2）可表示为

式中ωi为简支梁固有振动频率。

在qn（0）=q˙n（0）=z（0）= z˙（0）=0 初始条件下，可知上述方程组可求出唯一解。采用四阶Runge-Kutta 算法，利用数值计算方法依次可求得qn（t）、q˙n（t）、z（t）、z˙（t）时间序列，从而求出式（1）和式（2）中y 和z的解。

1.2 路面平整度函数计算理论

路面平整度是具有0 均值、各态历经性的高斯平稳随机过程，可利用路面平整度的功率谱密度获得路面平整度值[12]。采用由随机相位角组成的三角函数线性叠加模型计算路面平整度值。路面平整度的功率谱密度计算如下

式中：n 为空间频率；n0为基准空间频率；Gx（n）为空间频率n 对应的功率谱密度；Gx（n0）为基准空间频率n0对应的功率谱密度，又称为路面平整度系数，可通过查表获得；w 为频率指数，一般情况下取值为2。

由于汽车具有一定的隔振作用，仅选取对振动影响显著的有效空间频率区间进行计算[12]。根据三角级数法求解路面平整度值公式如下

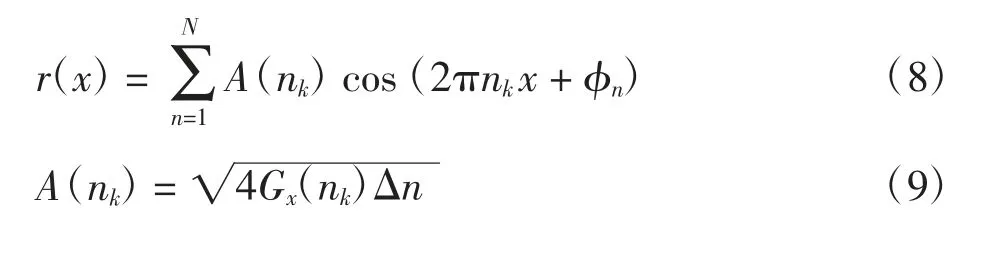
式中：nk为有效空间频率内的离散值；φn为[0，2π]中均匀分布的随机相位角；A（nk）为空间频率nk对应的三角函数振幅；Δn 为有效空间频率分辨率。

通过上述公式即可得到路面平整度等级A、B、C、D条件下的路面模型。

1.3 路面平整度对车-桥耦合振动的影响

由式（1）和式（2）可知路面平整度、车辆行驶速度是影响振动响应的因素，其中车辆行驶速度是可确定变量，路面平整度是随机变量，即路面等级与路面平整度值之间不存在唯一对应关系。为更好地研究车-桥耦合振动问题，采用统计学方法对同一等级路面随机产生100 个路面平整度样本进行分析，再依次代入式（1）和式（2）求解。选取简支梁桥跨中挠度冲击系数（简称简支梁桥冲击系数）作为统计量进行分析。

计算模型中参数设为：M = 30 000 kg；k = 1 ×106N/m；c=2×M×1.0 N·s/m；L=25 m；m=4 800 kg/m；EI=3.48×1010m4。简支梁桥在静载条件下跨中挠度为2.75 mm。

不考虑路面平整度的影响，当v=2 m/s、v=10 m/s时,简支梁桥跨中挠度位移曲线如图1 所示。二者跨中挠度最大值分别为2.76、2.81 mm，对应的冲击系数为1.004、1.022。计算结果表明：车辆行驶速度越大，简支梁桥冲击系数越大。

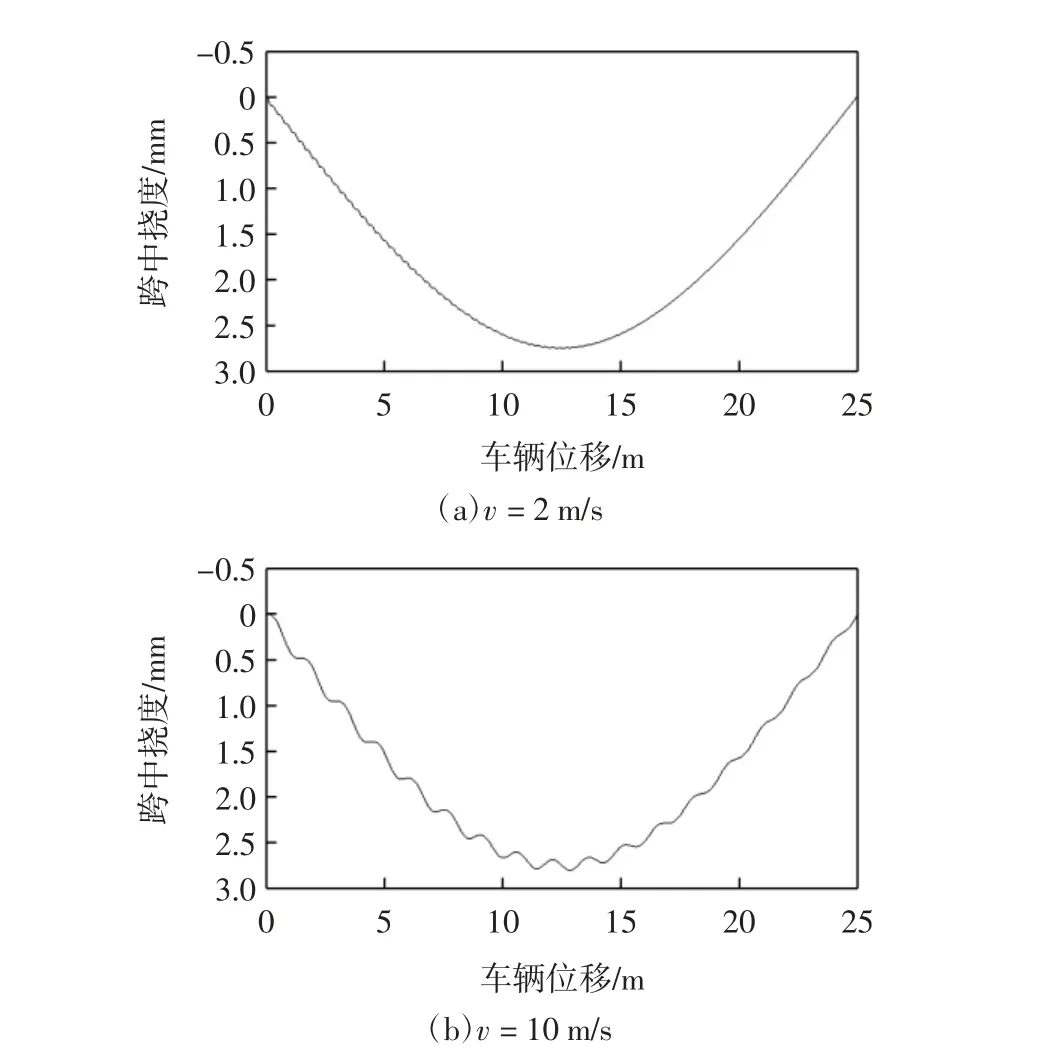
图1 跨中挠度位移曲线Fig.1 Mid-span deflection displacement curve

考虑路面平整度的影响，车辆在不同路面等级和不同匀速行驶速度下简支梁桥冲击系数均值如表1所示。计算结果表明：①冲击系数在同一路面平整度等级上满足正态分布；②路面平整度等级、车辆行驶速度均对冲击系数产生影响[13-14]；③当4 m/s≤v≤10 m/s时，车辆行驶速度对简支梁桥冲击系数影响很小，路面平整度对冲击系数影响很大；④当v ＜4 m/s 时，车辆行驶速度、路面平整度均对简支梁桥冲击系数有较大影响。综上分析，车辆行驶速度大于4 m/s 时，路面平整度是影响桥简支梁桥冲击系数的最主要因素。

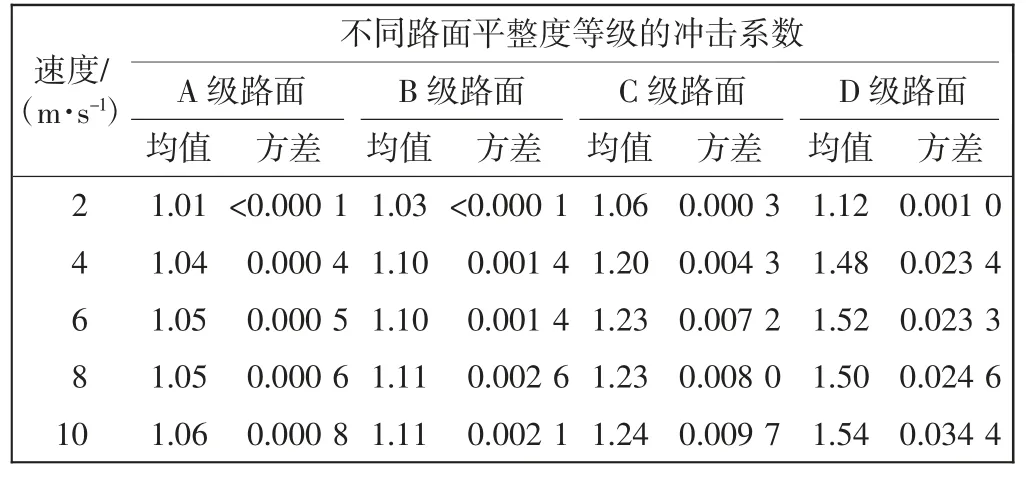
表1 不同匀速行驶速度下简支梁桥冲击系数统计表Tab.1 Impact coefficient statistics of simply supported beam bridge under the different constant driving speeds

2 跳车模型分析

路面平整度对车-桥耦合振动的影响不容忽略，但在实际工程中定量描述路面平整度非常困难，定性评价路面平整度引起的结果误差又难以控制。采用桥面枕木跳车试验方法，能够有效避免求解路面平整度，使得简支梁桥冲击系数可表示为仅与跳车高度、车辆行驶速度有关的函数。

2.1 桥面枕木跳车简化模型

桥面枕木跳车简化模型如图2 所示，其中h 为跳车高度。

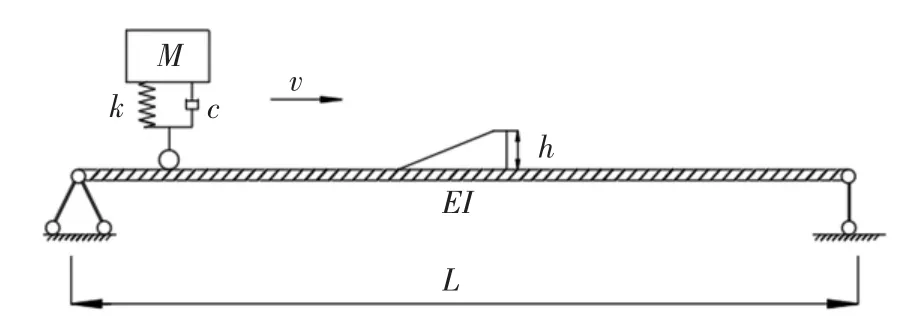
图2 桥面枕木跳车简化模型Fig.2 Vehicle′s bumping model of the crosstie

由于桥面跳车所用枕木高度、长度相对于车辆和桥梁尺寸很小，且车辆行驶速度缓慢（v≤10 m/s）。为便于计算进行如下假设：①车辆行驶过程中，除跳车瞬时外，车辆与桥梁始终保持接触；②不考虑枕木对桥面平整度值的影响；③弹簧-质量系统驶离枕木后在竖直方向上做有初速度的自由落体运动。由此可求出跳车后的边界条件，假设已求得跳车前速度（i）、位移z（i），则跳车后

2.2 桥面枕木跳车条件下车-桥耦合振动问题

模型参数与1.3 节保持一致，分别计算车辆行驶速度为4 ～10 m/s，枕木高度为5、10、15 cm，路面平整度等级为A、B、C、D 条件下简支梁桥冲击系数，计算结果如表2～表4 所示。

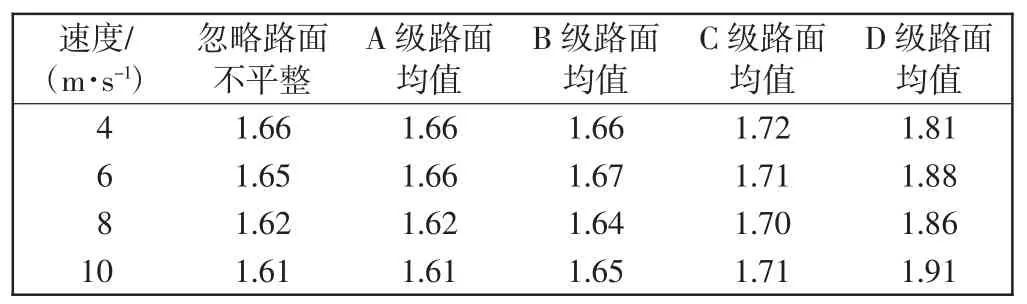
表2 跳车高度5 cm 时简支梁桥冲击系数统计表Tab.2 The coefficient statistics of simply supported beam bridge under 5 cm bump height of the vehicle

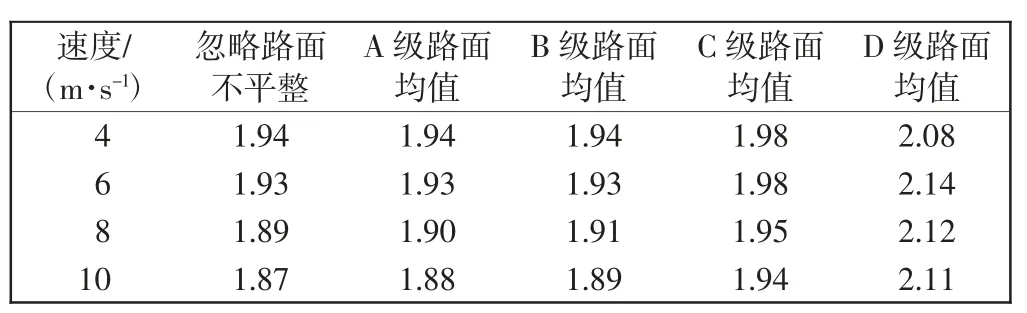
表3 跳车高度10 cm 时简支梁桥冲击系数统计表Tab.3 The coefficient statistics of simply supported beam bridge under 10 cm bump height of the vehicle

表4 跳车高度15 cm 时简支梁桥冲击系数统计表Tab.4 The coefficient statistics of simply supported beam bridge under 15 cm bump height of the vehicle

计算结果表明：①相同跳车高度下，相同路面平整度等级的简支梁桥冲击系数在不同车辆速度下具有相近均值；在相同车辆速度下，随着路面平整度变差，冲击系数逐渐增大；②对于路面平整度等级较好（不低于C 级）的简支梁桥，通过采用5 cm 高及以上的枕木跳车法计算的简支梁桥冲击系数能有效削减路面平整度的影响，与忽略路面不平整度的冲击系数偏差小于5%；③对于路面平整度等级较差（D 级)的简支梁桥，该方法效果不显著，采用15 cm 高的枕木跳车方法计算的简支梁桥与忽略路面不平整度的冲击系数偏差为6.6%；④为减小车辆行驶速度对枕木跳车条件下简支梁桥冲击系数的影响，建议车辆行驶速度采用4 m/s。

3 工程实例

以保定市某钢筋混凝土T 梁桥为工程实例，对枕木跳车方法进行验证。桥梁物理参数如下：EI=1.2×1010m4；L = 16 m；m = 6 750 kg/m；桥面路面平整度等级为B 级。采用加速度传感器测试桥梁跳车振动信号。加载汽车质量为30 t，其中前轴承重为6 t，后轴承重为24 t，车辆行驶速度5 m/s，枕木设置在桥梁跨中位置处，枕木高度h=15 m。跳车时，汽车前轴与后轴依次通过枕木，当后轴通过枕木时，前轴通过枕木引起的振动已衰减至很小，因此可认为前后轴的跳车冲击相互独立。为便于分析，这里仅考虑后轴对桥梁动态响应的影响，则弹簧-质量模型参数为：c=2×M×1.0 N·s/m；k=1×106N/m。

根据上述桥梁参数建立跳车模型计算的冲击系数均值为2.28，方差为0.002 8。

3.1 试验方法

汽车缓慢通过桥梁时，桥梁加速度响应将很小，引起桥梁的变形相当于跨中挠度的影响线，将该位移值定义为静位移。当汽车通过枕木发生跳车后将引起桥梁明显的加速度振动，此时通过加速度传感器测试分析到的位移是相对于静位移线的振动位移，定义为相对动位移。相对动位移与静位移的和定义为总位移[15]。简支梁桥跨中截面位移关系示意图如图3 所示。

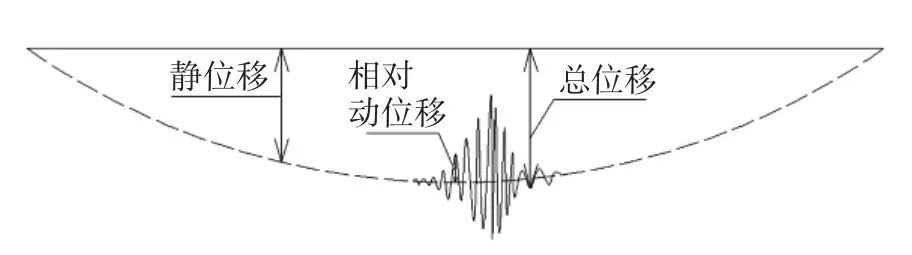
图3 简支梁桥跨中截面位移关系示意图Fig.3 Displacement diagram of simply supported beam bridge

试验中采用美国桥梁诊断公司（BDI）桥梁疲劳监测系统，采用动静对比分析计算冲击系数计算结果。加速度传感器用于采集跨中截面处的加速度信息，对加速度传感器所采集数据进行二次积分即为跨中相对动位移[16]。

工况1汽车缓慢行驶通过桥面，采集桥梁跨中挠度。试验结果表明，桥梁跨中最大静位移为1.80 mm。通过计算分析可知：当加载车后轴位于跨中位置时，此时前轴对跨中挠度的贡献值为16.6%，即前轴对跨中位移的贡献为0.30 mm，则加载汽车后轴引起的桥梁跨中挠度为1.80-0.30=1.50 mm。

工况2汽车以5 m/s 的速度通过桥面并在跨中位置进行15 cm 枕木跳车，通过布置在桥梁跨中位置的加速度传感器采集加速度信息。对加速度传感器所采集加速度信号滤波并进行二次积分可计算出桥梁跨中最大相对动位移1.84 mm，则跨中总位移为1.84+1.50=3.34 mm，加速度传感器实测数据与二次积分结果如图4～5 所示。

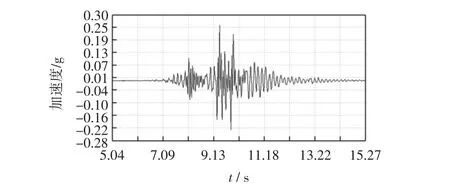
图4 加速度传感器实测数据Fig.4 Measured data of acceleration sensor

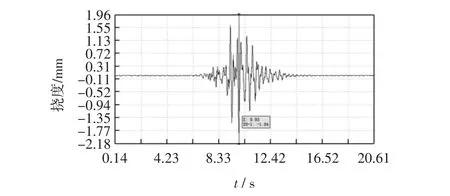
图5 加速度传感器二次积分结果Fig.5 Quadratic integral result of acceleration sensor

因此，15 cm 枕木跳车引起的桥梁跨中冲击系数为3.34÷1.50=2.23。

3.2 试验结果

通过上述实验可知：①车辆静载工况下桥梁跨中位移为1.50 mm；②15 cm 枕木跳车工况下桥梁跨中总位移为3.34 mm；③15 cm 跳车引起的冲击系数为2.23，同跳车模型计算的冲击系数2.28 相比仅相差2.2%，说明计算方法的正确性。

4 结语

通过车-桥耦合振动系统模型分析了车辆行驶速度、跳车高度、路面平整度对桥梁冲击系数的影响，并结合工程案例分析如下。

（1）利用数值计算方法求解车-桥耦合振动方程，模拟车辆冲击作用下桥梁振动响应情况，工程实例表明该方法能较准确反映简支梁桥在车辆荷载作用下的响应情况，可以用于计算简支梁桥动态响应冲击系数。

（2）路面平整度、车辆行驶速度均对简支梁桥冲击系数有影响。当v ＜4 m/s 时冲击系数随车辆行驶速度的增大而显著增大，当速度大于4 m/s 时，冲击系数随车辆行驶速度的增大而缓慢增长。相同加载条件下，同一路面平整度等级的冲击系数满足正态分布，不同路面平整度等级的冲击系数变化显著。

（3）枕木跳车试验能有效压制路面平整度对冲击系数的影响，当车辆行驶速度、路面平整度等级满足一定条件时（速度大于4 m/s，路面等级不低于C 级），5 cm 高跳车试验能够取得良好的测试效果。

（4）采用车辆简化模型分析了简支梁桥在车辆冲击荷载作用下的振动响应情况，为便于计算，对车辆和桥梁模型进行了一定的简化，因此计算结果存在一定误差。在后续的研究工作中将采用有限元方法建立车辆和桥梁全尺寸模型，分析简支梁桥在车辆冲击荷载作用下的动态响应情况。