基于LSTM的轨道交通进站客流短时预测研究

杜希旺，赵 星，李 亮

(河海大学 土木与交通学院，江苏 南京 210098)

城市轨道交通的发展作为城市公共交通现代化的重要组成部分，对于提高大中型城市客流运输量和运输效率、发展绿色交通以及缓解大城市道路交通拥堵具有重要意义。截至2020年年底，全国(不含港澳台)境内共有44个主要城市建设并开通投入运营的城市轨道交通线路233条，运营里程7 545.5 km，车站4 660座，实际运行列车2 528万列次，完成客运量175.9亿人次，进站量109.1亿人次。然而，随着我国城市化进程的不断加快，城镇化水平已突破60%，大量的人口涌入城市，给城市轨道交通带来巨大的压力和考验，尤其是在早高峰和晚高峰时，城市圈内的通勤需求给轨道交通带来更加沉重的负担。为加快建设交通强国的步伐，完善综合交通枢纽和物流网络，提高城市群和都市圈内部城市之间轨道交通通达性，提高运输效率，准确的掌握乘客的出行规律，对城市轨道交通各站点的客流量进行准确预测十分有必要。

目前，国内外针对轨道交通客流短时预测已经进行了较深入的研究。张智勇[1]等在站台短时客流特性的基础上，提出一种改进卡尔曼滤波短时客流预测模型。马超群[2]等考虑到了时间粒度对客流预测的影响，选取不同时间粒度下的时间序列，使用差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)进行预测。因为客流具有周期性，王莹[3]等在ARIMA的基础上使用季节性自回归移动平均模型对北京地铁进站客流进行预测，可以准确的判断出客流量的变化趋势。杨军[4]等基于灰色马尔科夫预测模型提出了一种可以预测大型活动期间的轨道交通大客流的模型。潘杰[5]等在灰色马尔科夫预测模型基础上，对原始数据进行滑动平均处理，再与无偏灰色模型方法结合，提出了一种滑动无偏灰色马尔科夫预测模型。传统的理论模型在轨道交通客流短时预测上，虽然操作简单，但是难以满足当前地铁进站客流波动变化的限制。

基于机器学习的计算机预测模型依靠算法，通过大量的训练数据进行特征学习，从而提高分类或预测的准确性，覆盖范围广，适应性好，受到了学者广泛关注。近年来，大量研究表明循环神经网络(recurrent neural network, RNN)在对时间序列预测时要比其他模型更准确，HEWAMALAGE[6]等通过RNN与统计模型的比较，认为其是一种有竞争力的预测方法。MADAN[7]等利用离散小波变换(discrete wavelet transformation,DWT)对时间序列数据进行分解，分别使用ARIMA和RNN进行预测，也充分说明RNN在时间序列方面的优势。但是，RNN无法解决长序列训练过程中梯度消失和梯度爆炸的问题。针对这一问题，MA[8]等提出了一种长短时记忆网络(long short term memory network, LSTM)，通过对北京市车速数据的测试，发现其预测精度和稳定性都能达到很好的效果。罗向龙[9]等根据交通流的时空相关性，提出一种基于K-最近邻与LSTM相结合的短时交通流预测模型。根据轨道交通客流的规律性和随机性，LIANG[10]等引入变分模态分解(variational mode decomposition,VMD)将客流进行分解，结合LSTM实现客流的预测。MA[11]等提出了一种由卷积神经网络和双向长短时记忆网络组成的并行结构模型，分别提取时间和空间特征，在模型中考虑了整个地铁网络的时空相关性。LSTM依靠自身优异的性能，经常被用来处理时间序列预测问题。

在轨道交通站点聚类上，K-means聚类方法因其简单高效、收敛快等优点被广泛使用。徐威[12]等选择路网密度、商业比例、居住比例、客流等作为特征指标，使用K-means聚类方法将苏州市轨道交通站点分为5类。邓评心[13]等采用定性、定量分析相结合，通过K-means聚类方法将苏州轨道交通系统的58个站点分为了4类。GAN[14]等使用K-means聚类方法将南京地铁站点分为7类，分别研究各类站点乘客出行特征与站点周围土地利用类型以及覆盖范围之间的联系。

大部分学者在进行客流短时预测研究时都注重在模型方法上的创新以提高预测的精度，但是较少从不同类型站点进站客流的差异性规律角度研究预测模型的适用性，往往在试验部分只选择一个站点进行验证，这样会存在偶然性。对此本文以南京轨道交通刷卡数据为研究对象，在各个站点客流的时序统计特征基础上，使用K-means聚类算法对南京轨道交通系统113个站点进行聚类，然后对各个类别站点的进站客流数据建立LSTM短时客流预测模型进行预测，比较各类别站点的预测结果，进而判断并分析各类别站点在使用LSTM短时客流预测模型的情况下预测精度上的差异。

1 模型构建

1.1 K-means聚类

K-means聚类是一种无监督学习的聚类方法，通过迭代算法不断更新各个聚类中心，从而寻找k个簇，使得聚类结果所产生的损失函数可以达到最小。算法步骤如下。

步骤1：选取聚类特征指标，在数据集中任意选取k个样本作为最开始的聚类中心；

步骤2：计算每个样本到聚类中心的欧式距离，并根据最小距离重新对相应样本进行划分聚类；

步骤3：计算每一类中各个样本的平均值从而得到一个新的聚类中心；

步骤4：重复步骤2和步骤3，直到满足最大迭代次数或者停止条件。

K-means聚类一般使用误差平方和(sum of the squared errors,SSE)作为评价目标函数，具体公式如下：

(1)

式中，ci表示第i个簇，p表示ci中的一个样本，mi表示ci中所有样本的均值。

1.2 长短时记忆网络

长短时记忆网络是一种在循环神经网络结构基础上进行了一些改进的神经网络模型，可以解决循环神经网络无法处理历史信息长距离依赖的问题，被广泛应用于时间序列建模问题。相对于RNN，LSTM在神经元中加入了输入门i、遗忘门f、输出门o以及内部记忆单元c四个部分。

1)输入门i：控制上一时间的输入xt和上一时间的神经元状态ht-1更新到神经单元中信息的数量。公式表达为：

it=σ(wixt+Uiht-1+bt)

(2)

式中，wi、Ui为权重系数矩阵，bt为偏置，σ为激励函数，一般取Sigmoid。

2)遗忘门f：控制上一时间的输入xt和上一时间的神经元状态ht-1中的信息被遗忘的数量。公式表达为：

ft=σ(wfxt+Ufht-1+bf)

(3)

式中，wf、Uf为权重系数矩阵，bf为偏置。

3)输出门o：控制当前单元状态ct中的信息输出到当前神经元状态ht中的数量。公式表达为：

ot=σ(woxt+Uoht-1+bo)

(4)

ht=otTanh(ct)

(5)

式中，wo、Uo为权重矩阵，bo为偏置。

4)内部记忆单元c：具备足够信息来计算更新神经单元状态，即根据神经元中的信息将上一时刻的单元状态ct-1更新为当前的单元状态ct。公式表达为：

(6)

(7)

1.3 模型构建

为探寻站点进站客流分布特征对预测精度的影响，本文使用K-means聚类方法对各个站点进行聚类，根据特征相似程度将站点分成几个类别，再通过LSTM对各个类别站点的进站客流进行预测，以比较不同类型站点之间在预测精度上的差别，寻找潜在影响预测精度的因素，揭示该模型对不同类型站点的适用程度，具体模型结构如图1所示。其中，全连接层中的每一个神经元都与上一层的所有神经元相连，用来把前面提取到的特征综合起来。隐藏层是对输入特征多层次的抽象，最终的目的就是为了更好地线性划分不同类型的数据。随机失活层的作用是防止模型训练过程中过拟合，是一种简单而又有效的正则化方法。

2 基础数据分析

截至2017年底，南京地铁已开通6条线路、共建成139座车站，线路总长为258 km，地铁线路总长度在中国大陆排名第5位(仅次于上海、北京、广州、深圳)、居世界第12位。本文选用南京市轨道交通2017年9月23日—2017年10月31日共计39 d，每日5：30—23：50进站的客流量为研究数据，由于部分数据缺失，只选择了其中113个站点为研究对象，并每隔10 min统计一次进站客流的人数，每个站点共有4 329条数据。

2.1 特征指标选取

时间序列种类多样，具有众多特征，每一个特征都对时间序列从某一角度上进行了一定的理解和认知。为提高每个类别中站点预测精度的相似性，特征指标的选取至关重用。时间序列的特征包括形态特征、模型特征以及结构特征三种类型，其中形态特征是指对时间序列在物理和形状上发生改变的一种表现形式；模型特征是指时间序列在变化过程中隐藏的规律；结构特征是指对时间序列的结构和内在变化的说明。

根据不同轨道站点的进站客流特征，本文选取偏度S、峰度K、工作日早高峰、晚高峰进站系数，非工作日早高峰、晚高峰进站系数，工作日客流标准差、非工作日标准差以及工作日客流系数作为聚类依据。

本文统计了南京轨道交通系统各个站点的进站客流，早高峰进站客流为选取时间7：00—9：00的进站客流，晚高峰进站客流为选取时间17：30—19：30的进站客流，工作日客流标准差为工作日全天10 min进站客流数的标准差，非工作日标准差为非工作日全天10 min进站客流数的标准差，偏度一般用来衡量数据分布偏斜方向和程度的大小，峰度是用来研究数据分布陡峭或者平滑的一种统计学测定。公式表达为：

(8)

(9)

(10)

(11)

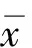
2.2 聚类结果

对轨道站点进行K-means聚类，关键在于确定k的值，k值过大将会导致聚类类型数量多于正常值，特征相似的站点将会被拆散；如果k值过小，又会导致特征不同的站点聚在一类。本文通过手肘法确定k值，以k值为横坐标，SSE为纵坐标，k值在5的时候曲率最高，因此k取5。通过SPSS数据分析软件进行聚类结果如表1所示。

表1 站点聚类结果Tab.1 Cluster results of metro stations

根据K-means聚类结果，类别1中只有新街口站，作为亚洲最大的地铁站为中华第一商圈服务，客流量要远远大于其他的几类车站；类别2和4中，站点为混合型，即站点周围多为居住型用地、高校、旅游景点或者商业用地；类别3中站点周围分布大量的居住型用地，以通勤客流为主；类别5中地铁站多为交通枢纽和商业中心。

2.3 进站客流时序特征分析

在5个类别站点中选取新街口站、夫子庙站、软件大道站、油坊桥站、奥体中心站、梦都大街站、南京南站以及鼓楼站共8个站点的进站客流作为各个类别的代表站点进行特征分析。各站点39 d客流量变化如图2所示，不同类型的站点客流量在不同的时间段上表现不同的特征。新街口站单日的客流量明显大于其他7个站点，在周末，新街口站、夫子庙站、南京南站以及奥体中心站客流量上升，梦都大街站、鼓楼站、软件大道站和油坊桥站客流量下降。在周五，除奥体中心站客流每周不一样外，其他站点客流均上升。国庆假期过后的三个星期里，进站客流量具有明显的周期性。

图2 各站点每日进站客流量变化对比Fig.2 Comparison of daily inbound passenger flow changes at various stations

影响进站客流量的因素众多，本文主要探究天气、温度、是否工作日以及站点周围用地属性对各个地铁站进站客流的影响。在39 d的数据中选取2017年10月16日—2017年10月22日完整一周的客流量单独研究。如图3所示，工作日和非工作日客流量呈现两种不同的特征，在客流量上，新街口站、夫子庙站非工作日的客流量要大于工作日的客流量，鼓楼站、软件大道站、油坊桥、奥体中心站以及梦都大街站工作日的客流量大于非工作日客流量，而南京南站的客流量无明显变化；就站点周围土地利用而言，新街口和夫子庙作为旅游商业用地，客流多以消费游玩为目的，进站客流非工作日的高峰时间比工作日时间提前并且持续时间更长。奥体中心作为文化体育设施用地，客流总量较小，在工作日有明显的早、晚客流高峰，非工作日客流高峰则与奥体中心举办的一些大型活动密切相关，大型活动的举办会导致附近站点客流急剧增长，活动结束后站点的进站客流增多，从而形成进站客流高峰[15]。油坊桥站附近多为居住用地，进站客流多为通勤客流，因此只有一个早高峰。南京南站作为对外枢纽，客流分布均匀，进站客流量与周围交通枢纽密切相关[16]。鼓楼站、软件大道站以及梦都大街站周围有办公商业用地，非工作日客流高峰比工作日开始时间延迟且客流量小，有早、晚高峰。

为了分析天气和温度对进站客流的影响，选取8个车站同为星期三的10月11日(雨)、10月18日(阴)和10月25日(晴)的进站客流，以确保具有其他相同的特征，如图3所示。可以发现，在不同的天气条件下各个站点的客流并未出现明显的变化。

图3 连续一周及不同天气下各车站每10 min进站客流量Fig.3 Inbound passenger flow of each station every 10 minutes in a continuous week and under different weather conditions

进一步探究各个因素对客流的影响，使用Spearman进行相关性分析，工作日与非工作日对客流相关性显著，天气与气温对客流的影响并不显著，如表2所示。因此，针对轨道交通客流短时预测，本文以是否为工作日作为预测模型的特征变量。

表2 Spearman相关性分析Tab.2 Spearman correlation analysis

3 模型预测结果

3.1 模型参数配置

建立LSTM网络预测模型对进站客流进行准确的预测，需要对模型的一些参数进行调试，例如，神经元数量、输入层的维度、时间步长、隐藏层的层数与维度和输出层的维度。

经过反复试验，将预测模型设置为两层的LSTM网络，中间为dropout=0.2的随机失活层，以防止过拟合，最后一层则为全连接层。输入层的维度为2维，用过去15个时间步长来预测未来，第一层网络中的神经元数量为100个，第二层网络中的神经元数量为50个。选定Adam优化器作为本文LSTM网络模型的优化算法，Adam优化器具有收敛速度快、实现简单、计算高效等优点，普遍被应用于神经网络模型中。损失函数是模型对数据拟合程度的反映，即模型预测出来的值与实际值之间的差值，模型拟合效果越好，损失函数越小，本文选择均方误差(mean square error,MSE)作为模型的损失函数。

将工作日的标签设置为1，非工作日的标签设置为0,look_back=15,batch_size=64。需要特别说明的是，因为数据中只有国庆一个节假日，且并无对节假日轨道交通客流短时预测，因此将国庆期间的工作日标签也设置为0。

将各个站点前35 d的数据(共3 885条数据)作为训练集，最后4 d的数据(共444条数据)作为测试集。使用基于TensorFlow后端的Keras框架进行测试，并使用训练集对该神经网络模型进行训练，训练次数设定为200次。

3.2 评价指标

为了评价模型的性能，使用均方根误差和决定系数两个指标对试验预测的结果进行量化评估。误差函数的计算公式如下所示：

1)均方根误差(root mean square error，RMSE)

(12)

2)决定系数(R-square，R2)

(13)

均方根误差反映了预测值与真实值之间的偏差，代表预测的总体可靠性，其值越小，说明预测偏差越小，即说明预测总体越可靠。决定系数取值范围为[0,1],数值越大表示模型拟合效果越好。

3.3 预测结果

通过LSTM对8个车站进站客流进行预测，不同类型站点的预测结果有所不同。如图4所示，模型在训练的过程中，在前30次的训练损失函数下降速度快，在训练的后期，损失函数均趋于收敛，训练效果较为理想，其中奥体中心站和梦都大街站前期损失函数下降较慢，损失值比其余站点大。

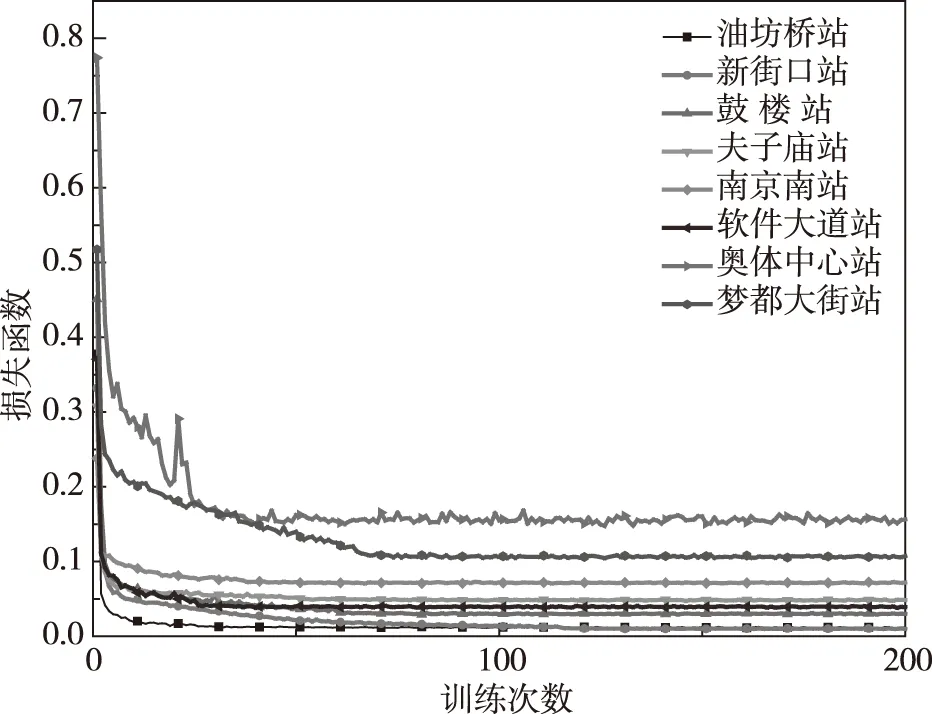
图4 损失函数图Fig.4 Loss function diagram

将处理好的测试集输入训练好的LSTM模型中，可以得到的预测结果如图5所示，包含两个工作日和两个非工作日，说明面对不同类型车站的进站客流，模型具有良好的准确性、可行性以及适用性。但是，由于不同类型站点客流的进站特征规律存在差异，模型预测的准确度也会有所不同，总体而言，客流波动性较小的站点预测精度要更加准确。南京南站进站客流受到高铁列车到站时间的影响，客流波动性大且无规律，奥体中心站受举办活动的影响，客流会在短时间内突然增加，给模型的训练提高了难度。相反，客流进站规律且上下波动相对较小的油坊桥站以及新街口站的客流预测结果决定系数可以达到0.99。

图5 各站点实际值与预测结果对比图Fig.5 Comparison of actual value and predicted result of each station

将考虑是否工作日影响的LSTM模型(LSTM-workday)与支持向量机模型(support vector machine, SVM)、RNN模型以及LSTM模型的预测结果进行比较，如表3所示。可以发现，考虑是否工作日的LSTM模型可以很好地对进站客流进行预测，预测结果要优于不考虑是否工作日的LSTM、RNN和SVM，其中，新街口站和油坊桥站客流预测的决定系数可达到0.99，奥体中心和梦都大街站客流预测的决定系数小于0.90。

表3 预测结果均方根误差与决定系数对比表Tab.3 Comparison of RMSE and of prediction results

进一步对各个类别站点的进站客流使用LSTM-workday进行预测，类别1和类别3的预测精度明显优于其他3个类别，类别4中的站点预测效果最不理想，预测决定系数大于0.95的站点只有18%，所有站点使用LSTM-workday预测决定系数均大于0.70，如表4所示。

表4 各类别站点LSTM-workday预测模型分布表Tab.4 Distribution table of LSTM-workday prediction model of various stations

4 结论

本文使用K-means聚类方法对南京地铁113个站点进行聚类，得到5个类别的轨道站点，对各个类别的站点的进站客流使用LSTM进行预测。

1)发现类别1和类别3的站点的预测效果最好，其次是类别2和类别5，最后是类别4。LSTM在预测周围用地属性是居住型的站点的进站客流最为准确，可以为用LSTM进行客流预测时站点的选择提供依据。

2)在预测方法上，使用LSTM预测模型，与SVM和RNN模型进行比较，添加是否工作日因素明显会提高模型预测的精度。

3)天气作为影响进站客流的重要因素之一，在工作日的影响要小于非工作日的影响，其对节假日客流量的影响较为显著。由于数据不足，考虑天气因素对模型的预测精度并不会有显著的提高。

4)不同类型站点的进站客流表现出不同的时空特征，为进一步提高模型的准确度，需要增加试验的数据，可以考虑更多的影响因素，宜对客流采用组合模型进行预测。