基于小波包分解的回转窑筒体故障提取研究

张绪金，张云

（武汉理工大学 机电工程学院，武汉 430070）

0 引言

回转窑是水泥工业的关键核心热工煅烧大型设备，日产5000 t回转窑一旦发生故障停产，将造成水泥企业巨大经济损失，停1 d仅产值损失高达200万元以上。由于窑生产条件恶劣、筒体内部窑皮分布不均匀、物料的雪球效应等诸多复杂因素的影响，使筒体温度分布不均匀发生热弯曲变形；同时，回转窑中心线偏差也会与窑弯曲同时作用造成对支撑处左右托轮的循环冲击载荷，引起托轮轴瓦温度升高，严重时可能导致托轮轴瓦烧坏而停窑[1]。因此，实现回转窑托轮振动信号的状态监测，对早期发现回转窑故障具有重要研究和实际应用价值。

在回转窑故障诊断领域，一些学者进行了相应的研究。张云等[2]为研究支承托轮的相对受力情况，自主研发了一套高精度的筒体椭圆度测量仪。张云和赵晨等[3]通过建立托轮振动模型，分析回转窑故障源与故障表征方法的对应关系，提出基于托轮振动特性的回转窑状态监测方法。郑凯等[4]通过建立托轮振动模型，采用EMD提取托轮振动信号的特征，建立回转窑状态监测系统。但是这些监测系统提取特征信号的模态混叠现象较严重，在噪声幅值系数和循环次数的确定方面，还存在一些困难。

因此，针对现有托轮位移信号处理方法的不足，本文提出一种通过对托轮振动信号进行小波包分解方法，以实现对回转窑筒体故障特征信号的提取，并以KH与RH的能量作为筒体故障程度的评价参数。通过处理实际托轮位移信号，验证了所提出方法的有效性。

1 小波包分解介绍

1.1 小波包概念介绍

小波包分解[5]是在小波变换基础上开发起来的时频分析法，具有可变、局部性和时频局部性的特征。它能够同时对非平稳信号进行高频和低频分解，同时对信号隐藏的特征信息进行有效反映，具有更高的时频分辨率。

小波分析中，尺度函数φ(t) 标准正交化生成的一组递推关系函数组如式（1）所示：

式中：n为振荡次数;k为位置指标;h0k和h1k分别为尺度函数导出的高通和低通正交滤波器系数;ω(t)为φ(t)的正交小波包。

理论上采集信号在正交小波包基上的投影系数叫做正交小波包系数，此方法系数是离散的。对于实际采集到的信号，小波包变换系数可表示为如下递推关系式：

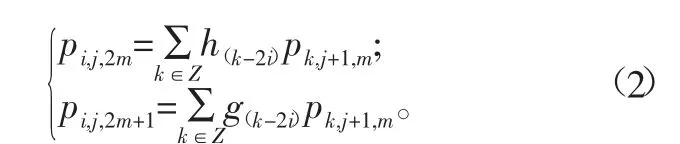
式中：pi,j,m为正交小波包空间中采集信号的小波变换系数；h(k-2i)和g(k-2i)分别为低通、高通共轭正交滤波器系数。

小波分解信号在中或高频率上则具有较差的时间频率信号分辨度，而在中或低频上则有较差的长时间频率分辨度。而小波包含率分解方法就是在此理论基础上提出的一种解决问题的全新方法，它可以算是现有信号小波分析方法中的一种较精细的方法，提高了信号分析时域的最高分辨率。

本文通过对回转窑运行过程中托轮振动信号进行3层小波包分解,从小波包分解重构图中提取筒体频率特征和托轮频率特征,小波包分解树结构示意图如图1所示。

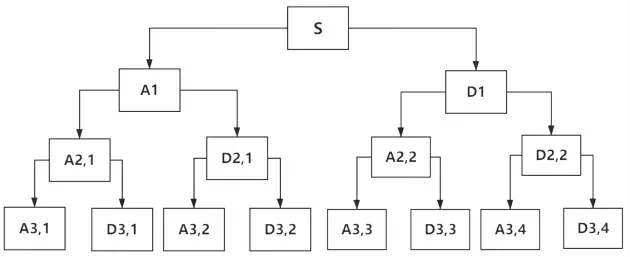
图1 小波包分解树结构示意图

如图1所示，小波包分解将原来的信号转化为两个部分，即高频和低频信号，左侧是低频信号，右侧为高频信号。从上述过程中可知，在小波包分解中，在高通和低通滤波器的作用下原始信号的信号量会缩减一半，而后再对分解后的信号继续进行分解。由此可以得出，信号分解系数的个数与小波包分解的层数有关。故小波包的重构算法如式（3）的递推关系式：

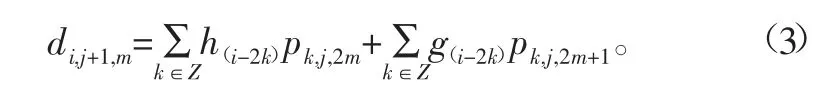
式中：h（i－2k）和g（i－2k）分别为低通、高通重构滤波器系数。

本文对回转窑运行过程中托轮的振动信号进行了采集，并用小波包变换对其进行了分解。提取重构信号中与筒体工作频率(KH)和托轮工作频率(RH)相关的振动频带小波包系数的能量值作为回转窑的故障特征信号。并以KH和RH的能量密度作为评估参数来分别反映筒体弯曲和各托轮受力状况的故障程度。

1.2 小波包特征提取过程分析

回转窑在运行过程中，随着筒体弯曲变形和筒体中心线的偏差会导致托轮受到不均匀的载荷，从而使托轮的振动频率发生改变。本文通过采集回转窑运行过程中托轮的振动信号，进行小波包分析，分解出托轮振动信号中的筒体工作频率成分和托轮工作频率成分，进行故障特征信号提取。

特征提取流程如下：

1）对采集的信号进行频谱分析，从而确定小波包分解时划分合适的频段。

2）确定小波包的分解层数。在进行小波包分解时，分解的层数与时频域信号的分析精度有着显著的关联。

3）对信号进行小波包分解与重构，得到重构后的信号频谱。

4）对重构后的信号频谱进行划分得到相邻且相等的频段，计算出各个频段的信号能量占比，选取合适的频带作为特征向量。

5）对特征向量进行分析。

回转窑故障分析的具体步骤如下：对采集托轮信号作预处理，通过小波分解和重构得到了第3层的小波包频带能量E3i，运用MATLAB软件展现各频带能量的占比，选取合适的频带作为特征分量，对特征分量进行Hilbert调制分析从而得到包络谱，根据包络谱中的显示，确定故障类型对应的振动频率。

2 基于托轮振动的回转窑故障分析

2.1 理论分析

回转窑在运行的过程中托轮的受力分析如图2所示。

其中：托轮受到自身重力沿x轴方向上的分力大小为Fr，筒体的静态载荷大小为Ts，筒体的动态载荷大小为Tr。故托轮总受力大小的表达式（3）如下：

其中托轮所受到的筒体静态载荷的大小不发生改变

式中：Mt为回转窑筒体在该挡处托轮的等效质量；θ为重力方向与x轴的夹角（如图2）。

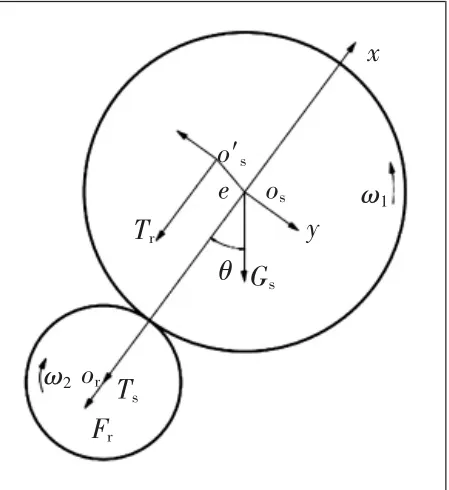
图2 托轮的受力分析图

若筒体发生偏心弯曲变形，假设变形量为e，将所产生的离心力进行分解，则托轮所受到的动态载荷的大小为

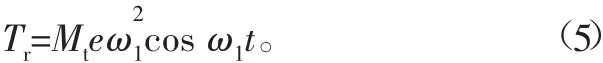
根据上述托轮振动模型，将托轮所受到动载荷等效替代到托轮轴中间位置，则托轮的变形挠度值为

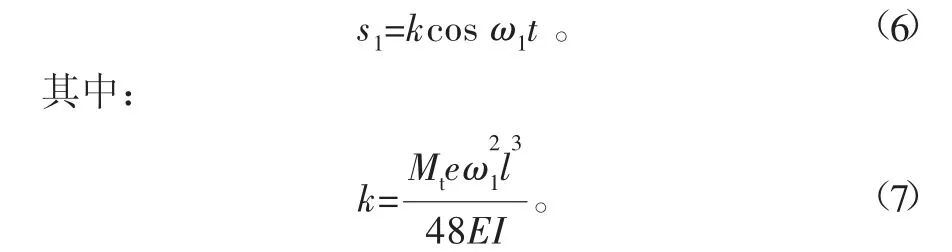
式中：l为托轮轴的长度；EI为托轮的等效抗弯曲强度。

托轮由于受到静态载荷TS所造成的变形量为τ，则其对应的挠度值为

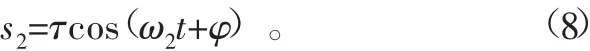
由上述分析可知，托轮的振动信号中包含了筒体频率(KH)和托轮频率(RH)成分，当回转窑某侧托轮超载受力过大时，则在该侧的托轮的载荷会增大，对应该侧RH谐波幅值会增大，即上述分析中s2的幅值会增大。当筒体的偏心弯曲变形较为严重时，对应KH的谐波幅值会增大，以及上述分析中s1的幅值会增大。

在回转窑运行过程中，由于回转窑筒体运转时间周期为15 s左右，托轮运行周期大约为筒体的1/3，回转窑运行系统为低速单向旋转转窑系统，频率不超过1 Hz，所以计算得知筒体的频率为0.06 Hz，托轮的频率为0.18 Hz。回转窑发生故障，则对应的托轮振动信号幅值会发生改变。

2.2 工程真实数据验证

为验证上述理论的正确性，通过对国内某一家水泥厂1条回转窑运行参数进行了现场数据的采集和处理分析。采集工具包括数据采集卡，非接触式电涡流位移传感器、霍尔开关及上位机，如图3所示。

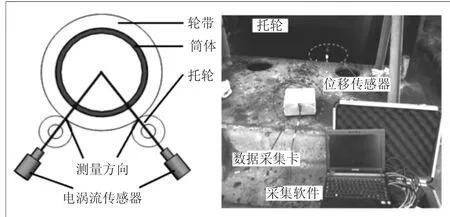
图3 窑托轮振动测量示意图

本文以该窑一挡右托轮数据为例，采用小波包分解方法提取故障特征频率，首先对信号采用3层的demy 小波包分解，将4 Hz 有效信号分解为8个频段，如图4（a）所示，表明3层的小波包分解过程。图4（b）为3层小波分解之后各频带能量分布图，由采集频率可以计算出各频带之间的间隔为0.25 Hz。

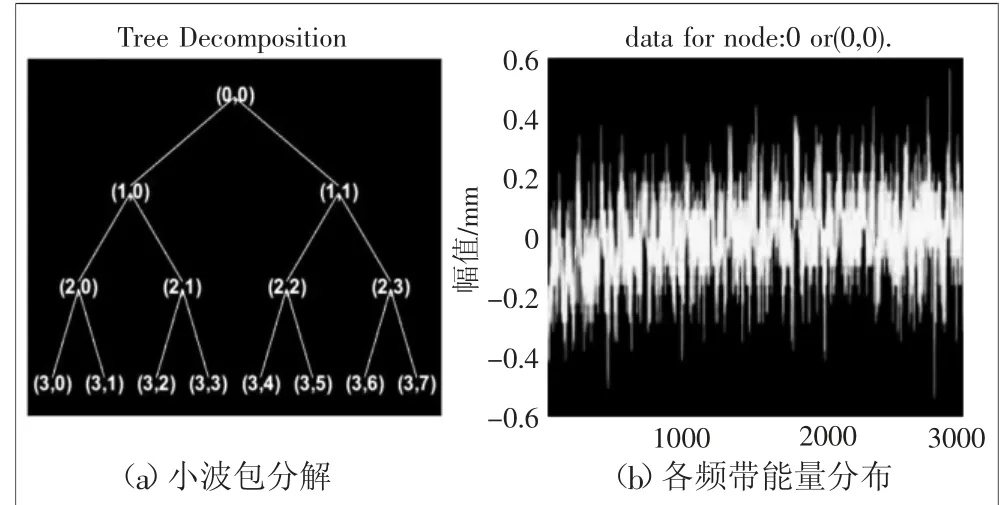
图4 小波包3层分解示意图

根据图5可知信号在第1频带（0 ～0.25 Hz）处能量占比最高，将原始信号在该频带处分解得到小波包分解系数，并根据分解系数对原始信号进行重构，如图6所示。

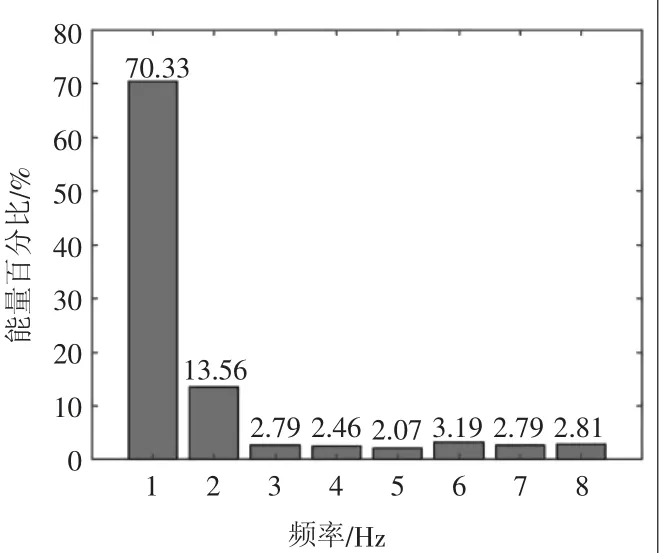
图5 分解后各频带能量占比图

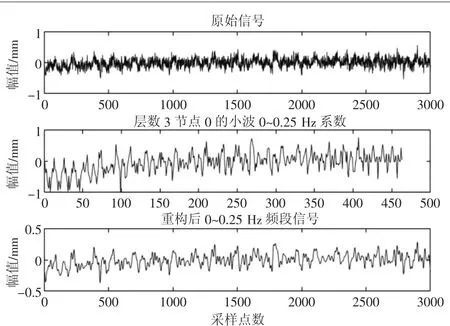
图6 小波包分解系数和重构图

重构后的信号进行Hilbert变换后，进行包络谱分析得到结果如图7所示，由图中可以看出，信号在0.06 Hz和0.18 Hz周围的幅值变化较为明显，它们分别是筒体工作 频 率(KH)和托轮工作频率(RH)。

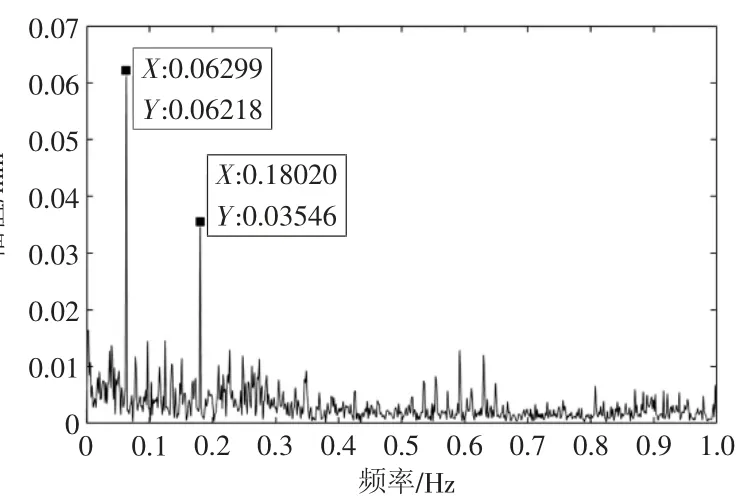
图7 重构信号的包络谱图

3 基于小波包分解的窑筒体故障识别

对该水泥厂回转窑所有的托轮进行振动信号采集，提取重构信号包络谱频率0.06 Hz即筒体工作频率（KH）和0.18 Hz即托轮工作频率（RH）的分量，对带有筒体、托轮运转状态信息的故障特征信号进行处理分析。各挡提取到的KH和RH结果如图8所示。

图8 托轮信号分解后的KH和RH幅值图

3.1 对筒体弯曲故障进行识别

由于回转窑各挡支撑位都有左右两个托轮，为了综合判断挡位所在处的筒体偏心大小，现引入平均能量密度来进行判断。定义如式（9）所示：式中：ΔE为能量密度；xi为信号量；n为信号长度。

回转窑各托轮处筒体工作频率信号能量密度计算结果如表1所示。由表1可知，各挡的筒体工作频率(KH)平均能量密度比较结果是：2挡大于1挡；2挡大于3挡。

表1 筒体工作频率(KH)平均能量密度ΔE

在窑旋转1圈中，使用窑筒体弯曲激光测距仪对各挡托轮支撑处筒体截面进行测距扫描测量。采用最小二乘法对测得的筒体截面距离变化数据进行拟合处理。各挡处截面筒体偏心的结果如表2所示。由此得出，2挡处筒体偏心大于1挡处，也大于3挡。通过对表1和表2的分析对比，KH平均能量密度和窑体偏心值相互对应，说明筒体信号的平均能量密度可以对应反映不同挡位筒体偏心故障的严重程度。

表2 各挡位截面筒体偏心值e mm

3.2 对托轮超载受力故障进行识别

由图8中右方的托轮工作频率的幅值图可知，1挡左托轮受力明显大于右托轮，2挡左右托轮受力相当，3挡左托轮的受力比右托轮大。而造成这种超载受力不均匀的现象是与回转窑筒体在运行过程中会发生了中心线偏差有关。

采用张云等[10]研发的回转窑椭圆度测量仪对各挡位筒体的椭圆度进行测量，椭圆测量仪随筒体旋转测出测点的弹性形变量即椭圆度曲线，仪器经过左右两个托轮时有两个小波谷曲线，它可以线性反映左右两个托轮受力的大小比例值。处理得到的曲线如图9所示。

图9 各挡位筒体的椭圆度曲线

从图9中可以看出，一、三挡处左托轮受力均大于右托轮。通过把图8中的右图与图9中的两个小波谷做对比分析，由此证明（小波包分解得到的）托轮工作频率(RH)的幅值可以正比例地反映各个托轮受力超载的故障程度。

4 结语

本文通过理论分析得出在托轮位移信号中包含了筒体频率和托轮频率谐波。通过对回转窑两侧的支承托轮位移的实际工程信号采集并进行分析处理，采用小波包分解方法能够有效地提取窑故障的两个特征频率，即筒体工作频率(KH)与托轮工作频率(RH)。同时验证了KH和RH的能量密度能分别有效反映出筒体偏心弯曲变形和各个托轮超载受力的故障程度，证明了该方法的有效和可行性，为回转窑筒体和托轮的故障检测判断提供了一种新的解决思路。