基于大数据的燃煤电站空冷岛运行实时优化策略

聂椿明， 安留明， 徐 钢， 陈 衡， 李 季

(华北电力大学 能源动力与机械工程学院，北京 102206)

据中电联发布的2019—2020年度全国电力供需形势分析预测报告统计，2019年全年全社会用电量达到7.23×1012kW·h，比2018年全年增长了4.5%，全国人均用电量达到5 161 kW·h，人均生活用电量732 kW·h。截至2019年年底，全国发电装机容量突破2×109kW，火电装机容量达1.19×109kW，其中水电、核电、风电和太阳能发电量快速增长，分别增长5.7%、18.2%、10.9%和26.5%，从以上数据可以看出我国用电需求正在不断增加，且在未来一段时间内，火电仍将占据发电行业的支柱地位[1-2]。

由于我国水资源较缺乏，人均水资源在全世界排名第122位，且淡水分布不均，因此我国装机容量受到限制。火电厂直接空冷技术提供了可行的解决方案，这对于我国富煤缺水的“三北”地区具有重要意义[3]。随着近年来节能理念及可持续发展理念的不断发展，给电厂的经济性和稳定性提出了更高的要求，优化背压研究显得尤为重要[4]。

近年来，由于大数据方法的飞速发展，数据管理、数据价值的利用已经成为判断企业实力的一个重要因素，也成为未来各个行业的发展方向[5]。传统火电厂直接空冷机组通过现场热力实验得出的背压控制曲线来控制机组对应负荷下的设计背压值，从而调控指导机组运行。近年来，国外学者结合数值分析方法[6-7]进行空冷机组背压优化，也有学者运用大数据方法[8]进行空冷机组冷端优化。基于这些背压优化研究，笔者提出基于最佳数据库的背压实时优化方法，可以更加有效地吸收历史数据中有效果的运行工况点，从数据上优化了最佳背压寻找逻辑，使得最佳背压更符合提高机组净发电功率的要求，对模型训练也有一定程度的优化。

1 研究方法

1.1 案例

选取河北某2×600 MW超临界直接空冷燃煤机组为研究对象，其空冷系统由56台风机组成，40台顺流凝汽器风机，16台逆流凝汽器风机，风机叶片为宽叶低噪型，每台风机叶片数量为6个，风机直径为9.754 m，额定转速为73 r/min，额定风量为573 m3/s。空冷机组的换热管束由单排翅片管组成，翅片管材料为碳钢/铝翅片，翅化比(散热面积/迎风面积)为123，总散热面积为1 423 460 m2。

1.2 最佳背压分析方法

在机组运行过程中，降低机组背压可以使汽轮机的理论比焓降增大，从而增加汽轮机出功，提高其循环效率。然而想要增大机组出功，不论是从安全角度、设计角度还是从运行角度都不是简单地降低背压能够实现的。在空冷机组运行过程中，降低机组背压主要依靠增大风机群耗功，然而风机群耗功在厂用电中的占比较高，盲目增大风机群耗功可能会使得降低背压所多发的电少于增大风机群耗功所消耗的电，得不偿失。而理论最佳背压[9]即为当其他因素保持不变时，降低背压导致的机组电功率增量ΔPel减去降低背压时风机群耗功增量ΔPp的值达到最大时的背压值[10-11]，即

max ΔP=max(ΔPel-ΔPp)

(1)

式中：ΔP为机组净发电功率增量。

而基于神经网络[12]所采用的最佳背压逻辑为建立背压与机组净发电功率ΔP之间的数据关系，其中风机耗功的计算公式为：

(2)

式中：U为风机电压；I为风机总电流；φ为风机额定相位角。

针对目标数据集建立由历史最佳数据库训练所得预测模型，用于对背压进行预测优化；评估模型数据尽量保证数据完整性以及评估的真实性，用于对优化结果进行评估。

历史最佳数据库是通过对历史数据运行工况较好的点进行筛选，选出运行工况类似的较好点进行平均值选取。具体筛选方法是通过筛选相同负荷及环境温度下的工况点中净发电功率较大的前30%的点作为最佳数据库数据。由于实际运行数据中负荷与环境温度测点数据没有精准的整数，所以设置负荷与环境温度偏置范围可以将近似的运行工况点集中在1个集合，方便在其中进行最佳数据库的筛选。负荷间隔1 MW，环境温度间隔1 K，负荷筛选偏置范围为0.5 MW，环境温度筛选偏置范围为0.5 K。数据筛选过后的数据集就成为历史最佳数据库，为之后的预测模型提供运行工况较好的建模数据。

具体的背压优化思路为：首先基于历史实际背压生成1个背压范围，考虑到现场的背压最大偏置为±2 kPa，所以将背压偏置设置为±2 kPa，背压间隔取0.01 kPa，其他数据不变。将边界条件与背压序列一同代入预测模型中，得到背压范围内的一系列机组净发电功率，将其与实际机组净发电功率进行比较，最大机组净发电功率对应的背压值即认为是最佳背压，当最大机组净发电功率是实际机组净发电功率时，实际背压即为最佳背压。将最佳背压序列经高斯平滑之后代入评估模型中进行评估，得到的机组净发电功率为优化后机组净发电功率，与实际机组净发电功率比较即可得到节电量。图1为历史实际数据的某点最佳背压分布。可以看出，在此实时运行工况下背压在10 kPa左右时，机组净发电功率达到最大值，对应的背压即为此运行工况下的最佳背压。

图1 某实际工况最佳背压Fig.1 The optimal back pressure in an actual condition

最佳背压思路逻辑导图见图2。图中NAN值含义为Not a Number，即为坏值，需要在处理数据过程中筛除。

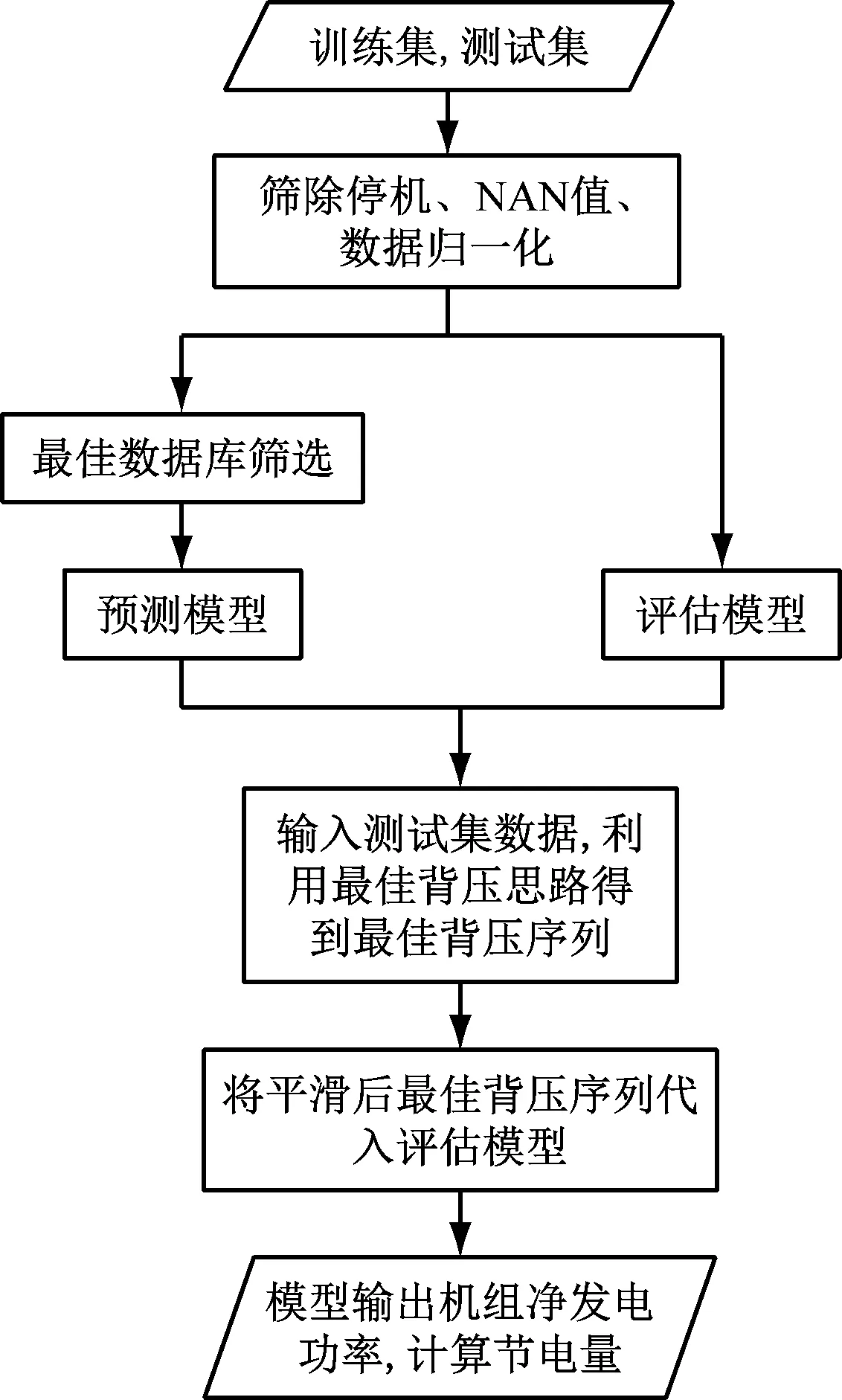
图2 最佳背压优化思路流程图Fig.2 Flow chart of optimal back pressure optimization

1.3 机器学习方法

采用的机器学习方法为BP(Error Back Propagation Training)神经网络[13]，用来实现对历史运行数据的建模和拟合。BP神经网络的学习函数、激励函数、隐藏层层数和神经元个数等调节参数均会对模型的精度以及最后的预测效果产生影响，但在建模过程中更为重要的是数据本身的特点。

BP神经网络的优点在于不需要确定输入输出之间的数学关系，它通过不断地训练和逼近某种学习规则，从而在数据输入之后通过训练得到的规则得出输出值；BP神经网络主要分为前向传播和误差反向传播2个过程。计算误差时正向进行，反向调整权值和阈值，通过调整输入节点与隐藏层节点的权值以及隐藏层节点与输出节点的权值和阈值，使误差沿梯度方向下降。经过反复训练，当误差最小时，确定各层对应的权值和阈值，并停止训练[14]。BP神经网络原理图如图3所示。

图3 BP神经网络原理示意图Fig.3 BP neural network schematic diagram

2 数据观察及预处理

2.1 数据观察

首先从电厂分布式控制系统(DCS)中提取出机组历史运行数据，数据间隔为30 s。2018年全年数据有1 051 200组。结合其他文献中分析的背压影响因素以及DCS情况，能够读取的测点参数主要有机组负荷、背压、环境温度、环境风速、环境风向、主蒸汽参数、凝结水温、凝结水质量流量、风机电流、风机转速和风机轴温等。对2018年全年运行数据进行观察，以2018年全年机组负荷、背压和环境温度曲线图(图4)为例，可以看出机组负荷和背压在6月底及9月底有对应关系，全年环境温度在-10～40 ℃。

2.2 数据预处理

由2018年全年机组负荷和背压曲线可知，机组有2次停机，一次发生在6月底，一次发生在9月底。机组负荷与背压能够相互对应，所以为了方便观察运行数据之间的关系以及规律，需要将停机工况的数据筛除，从现场DCS中取出的数据不仅包含停机工况的数据，还会有很多无法读取数值的NAN值，因此需要先对数据进行筛除。此外，由于数据之间会有数量级的差异，为了避免大数吞小数的情况，对数据进行归一化处理，将数据按比例映射到[-1 1][15]。筛除停机工况和NAN值之后的2018年全年数据有934 269组。处理后的2018年全年主蒸汽质量流量及2018年全年风机群耗功如图5所示。

最后对机组参数、风机参数、环境参数及其范围进行整理和分类，结果见表1。

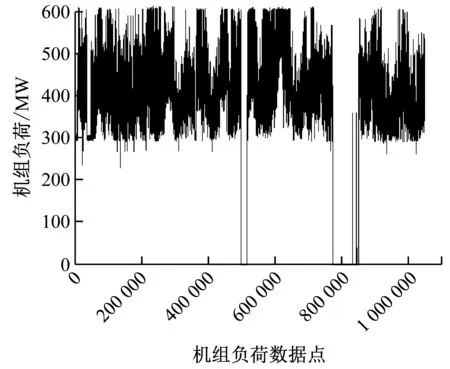
(a) 2018年机组负荷运行数据(b) 2018年背压运行数据(c) 2018年环境温度数据图4 2018年全年数据时序图Fig.4 The whole year data sequence chart in 2018

表1 机组各测点运行参数范围

2.3 相关度分析

在空冷机组实际运行过程中，背压是机组经济性运行的关键调控参数，不论是对机组的经济性还是安全性进行评估，都需要了解影响背压的因素，空冷系统直接与外界环境接触，受环境影响较大，且全年背压范围变化较大，冬季还需要考虑安全性问题，所以理论上环境温度、主蒸汽压力、主蒸汽温度、主蒸汽质量流量、环境风速和环境风向等因素均可能会对机组背压造成影响[16]。观察其他历史运行数据可以得到如下规律：夏季温度较高时，背压、风机耗功和风机轴温等参数较高，冬季温度较低时这些参数则较低。理论上的背压影响因素如图6所示。

图6 理论背压影响因素Fig.6 Theoretical influencing factors of back pressure

利用皮尔逊相关度系数[17]计算各影响因素与背压的相关度情况，皮尔逊相关度系数计算公式如下：

(3)

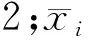
计算之前限定机组负荷和环境温度，以便合理地对各主要因素与背压的相关度进行分析，柱状图分析结果如图7所示。

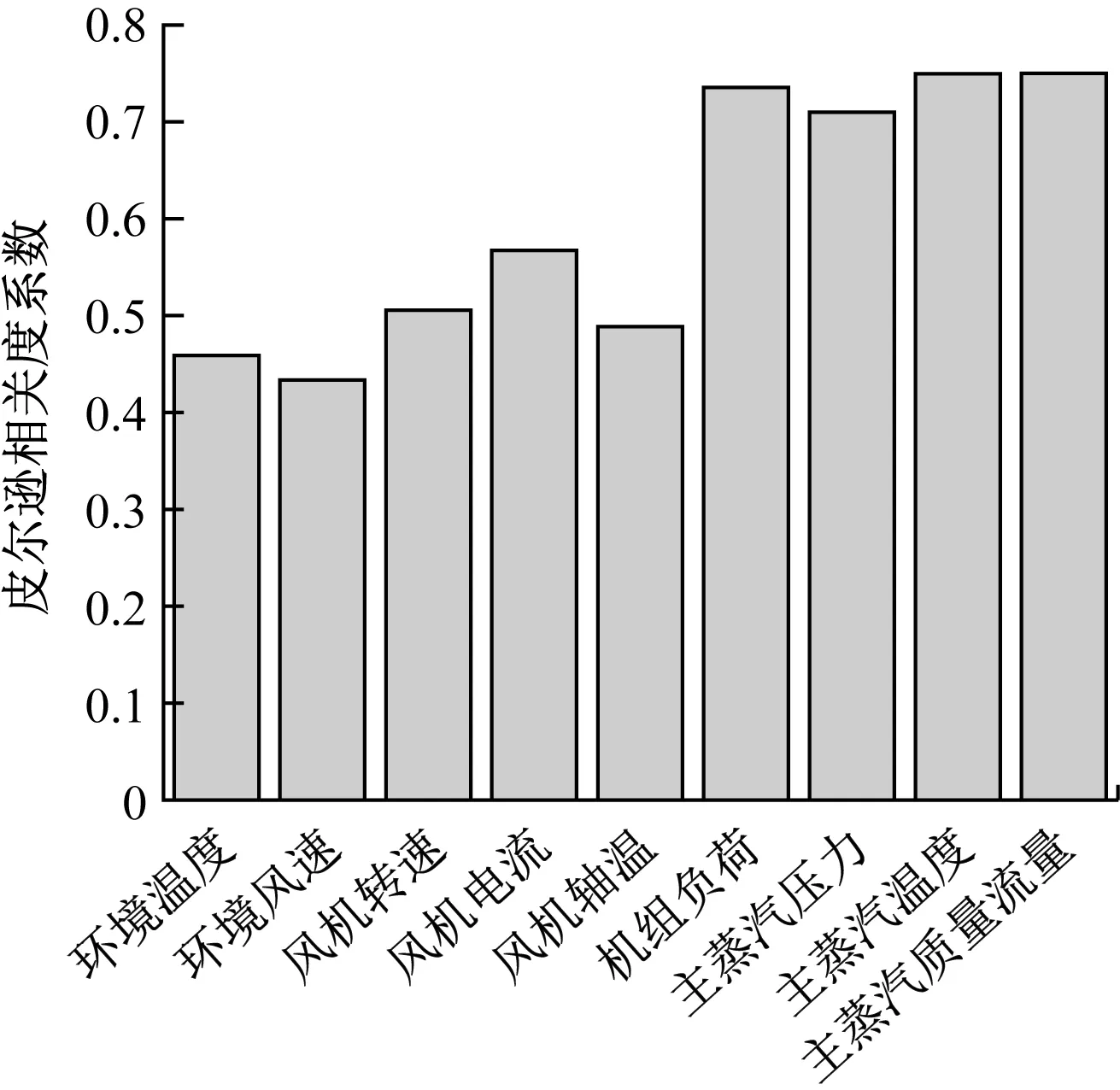
图7 各因素与背压的皮尔逊相关度系数Fig.7 Pearson correlation coefficient diagram betweenvarious factors and back pressure

由图7可以看出，限定边界条件后环境参数和风机参数与背压的相关度系数在0.5左右，机组负荷和主蒸汽参数与背压的相关度系数在0.75左右。

3 模型建立及评估

3.1 模型建立

模型建立过程如下：

(1) 数据预处理：输入训练集和测试集数据，删除停机工况数据和NAN值，对数据归一化。

(2) 训练模型：筛选所得的最佳数据库数据与测试集数据，分别建立以背压为自变量,多种因素作为边界条件输入、机组净发电功率为输出的预测模型和评估模型。

(3) 寻找最佳背压：将测试集数据输入预测模型，基于实际背压生成对应的背压范围，其他条件不变逐个预测机组净发电功率，挑选机组净发电功率最大时对应的背压为最佳背压。

采用最佳背压思路和2018年1月—6月的数据建模，预测2018年7月运行数据，将数据归一化后建立以背压为自变量，环境温度、主蒸汽压力、主蒸汽温度、主蒸汽质量流量、凝结水质量流量、风机轴温、环境风速和给水质量流量为边界条件，机组净发电功率为因变量的模型[18]。由于背压作为自变量，因此电厂实际运行中风机转速作为调节背压的主要手段并不能作为边界条件输入模型。经过多次尝试，模型学习函数采用trainlm，传递函数采用tansig和purlin。

3.2 模型评估

采用误差分析评估模型的性能，误差指标有平均绝对误差MAE、平均相对误差MAPE、均方根误差RMSE和确定系数R2，其计算公式如式(4)～式(7)。

(4)

MAPE=sum(|y′-y|×100/y)/n

(5)

式中：y′为预测值；y为实际值。

(6)

式中：xr为一组测量值与真实值的偏差。

(7)

参考其他文献中误差的计算方法，对比分析了单、双隐藏层以及不同神经元个数时模型的准确性[19]，对每种神经元分类分别试验5次，得到的结果取平均值，最终确定了模型参数。当预测模型采用单隐藏层，神经元个数为7，评估模型采用单隐藏层，神经元个数为7时模型的平均相对误差最小，即此时的模型拟合结果最可靠，如表2所示。

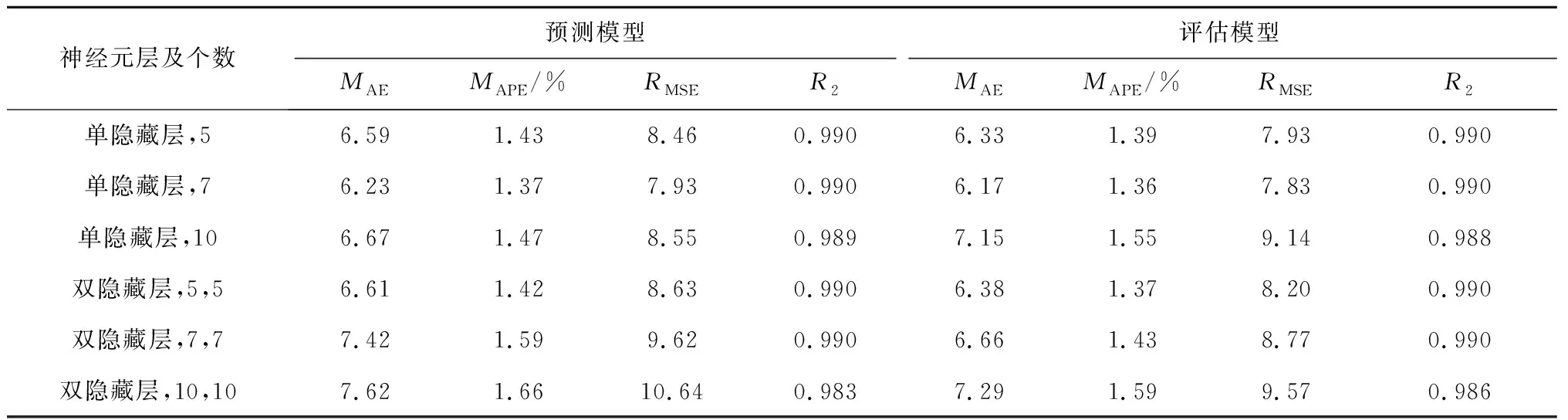
表2 模型性能

根据表2所得结果，本文第4节中的节能效果评估所使用的预测和评估模型将从神经元个数为7的模型中选取误差最小的模型。

4 计算结果及分析

4.1 时序分析

笔者主要对2018年7月的数据进行节能效果评估，考虑到数据的完整性，为了尽可能提高模型可靠性和精度，训练集数据采用2018年1月—6月的数据，由前文试验得到的最佳模型参数设置模型，采用式(8)来评估节电量。

(8)

式中：ΔW为计算节电量，kW·h；P2为每个时间点对应的优化机组净发电功率，MW；P1为每个时间点对应的实际机组净发电功率，MW。

2018年1月—6月原始数据总共有521 280组，经过数据预处理，筛除异常工况后还剩下486 619组，用于建立评估模型。经过处理的数据再进行最佳数据库筛选，剩下158 419组数据，用于建立预测模型。对2018年7月的数据采用最佳背压思路进行评估，由于7月整体数据量较大，图8和图9给出了优化前后数据差值对比曲线。由图8可以看出，优化背压大部分集中在实际背压±1 kPa范围内，有少数波动较大的优化背压与实际背压差值在±2 kPa以内。由图9可以看出，优化机组净发电功率与实际机组净发电功率差值集中在10 MW以内。

图8 2018年7月实际背压与优化背压差值曲线Fig.8 The difference curve between actual back pressure andoptimized back pressure in July,2018

图9 2018年7月实际机组净发电功率与优化机组净发电功率差值曲线Fig.9 The difference curve between actual net generating powerand optimized net generating power in July,2018

抽调2018年7月月初、月中和月末各200个样本点，图10～图12给出了这些样本点优化前后背压和机组净发电功率的对比情况。

由节电量计算公式可以计算得到2018年7月单月节电量ΔW为961 091.27 kW·h。观察图10～图12，其中各段样本点的优化背压在实际背压附近上下波动，这是由于机组在不同运行工况下，模型输出结果判断改变背压后，机组净发电功率是增大的，并且由于当时机组实际运行工况的差异，7月月初、月中和月末的优化背压与实际背压之间也存在一定差异。

4.2 负荷分段分析

为观察不同负荷下的优化结果，将优化结果按负荷范围300～330 MW、>330～360 MW、>360～390 MW、>390～420 MW、>420～450MW、>450～480 MW、>480～510 MW、>510～540 MW、>540～570 MW、>570～600 MW、>600～630 MW分别进行统计，由于每个负荷段数据量存在差异，因此计算比较每个负荷段内每30 s的平均节电量，结果见表3。

(a) 背压对比曲线

(b) 机组净发电功率对比曲线图10 2018年7月月初样本点数据优化前后背压、机组净发电功率对比曲线

(a) 背压对比曲线

(b) 机组净发电功率对比曲线图11 2018年7月月中样本点数据优化前后背压、机组净发电功率对比曲线

(a) 背压对比曲线

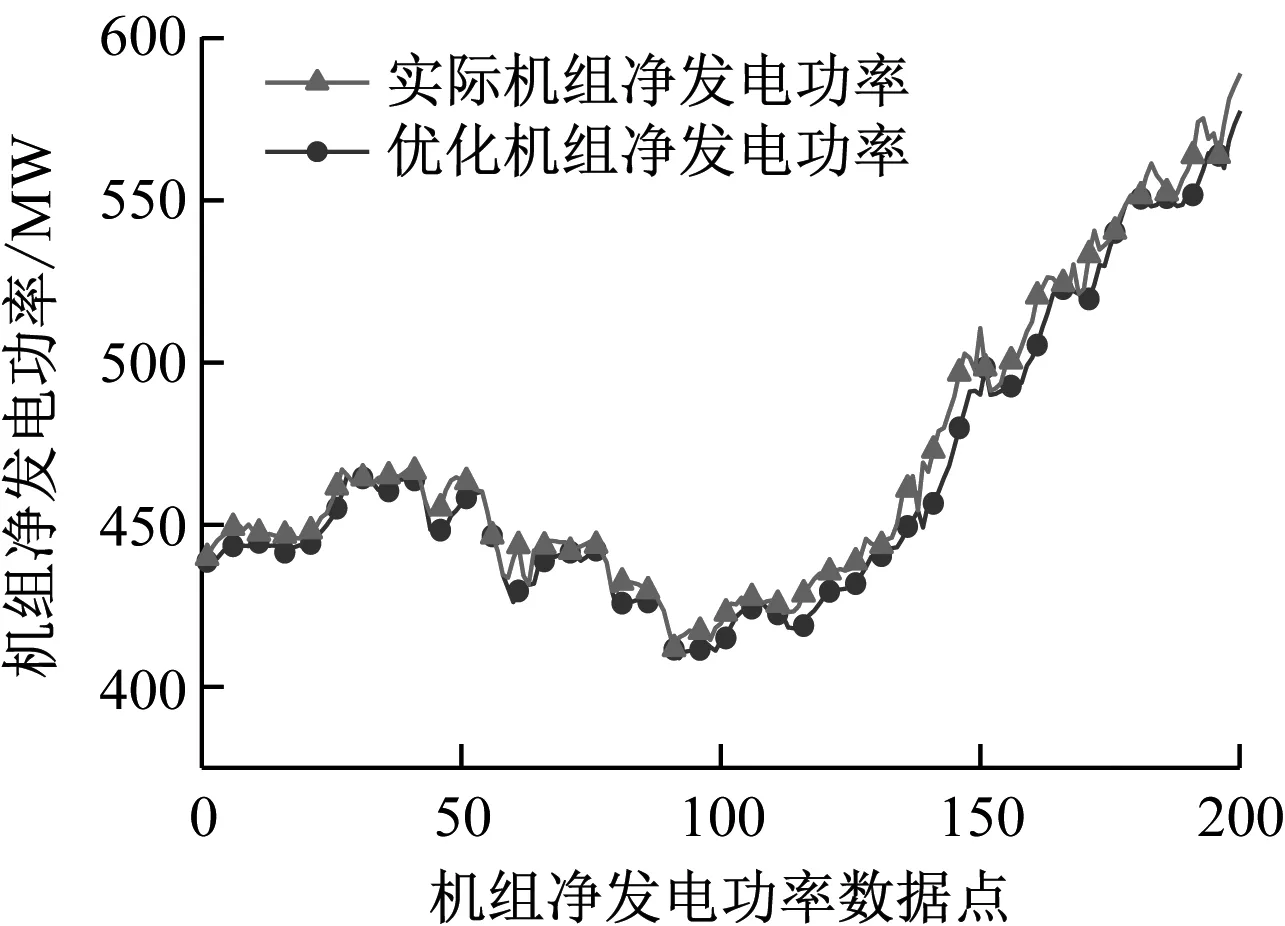
(b) 机组净发电功率对比曲线图12 2018年7月月末样本点数据优化前后背压、机组净发电功率对比曲线

由表3可以看出，当机组负荷在360～570 MW时优化效果较为明显，30 s平均节电量在10 kW·h以上，而在低负荷和高负荷时节能效果并不明显，30 s平均节电量在10 kW·h以下，说明最佳背压思路在机组处于中负荷运行时的节能效果较好。由于机组实际运行中会根据现场控制曲线的最佳背压进行调节，从物理机理上分析，机组在低负荷和高负荷段运行时，控制曲线对应的指导背压变化范围较小，机组在此工况下运行时的背压数据本身变化范围较小，使得模型预测得到的优化机组净发电功率与实际机组净发电功率相差较小，与实际情况较为符合。

表3 不同负荷分段每30 s的平均节电量

4.3 环境温度分段分析

2018年7月环境温度最低为21.21 ℃，最高为34.61 ℃。为了观察不同环境温度下的优化结果，将优化结果按照环境温度20～25 ℃、>25～30 ℃、>30～35 ℃分别进行统计，由于数据量的差异，因此计算比较每个环境温度范围内每30 s的平均节电量，结果见表4。

由表4可知，当机组运行环境温度为20～30 ℃时，优化效果较好，每30 s的平均节电量基本保持在10 kW·h以上。当机组运行环境温度在>30～35 ℃时，优化效果不明显，每30 s的平均节电量为1.01 kW·h，说明最佳背压思路在当月较低环境温度时优化效果较好，从物理机理上分析，当环境温度较高时，风机转速已经达到最大，考虑到风机轴温过高的问题，机组此时的背压调节空间很小，实际背压变化范围较小，导致模型预测得到的优化机组净发电功率与实际机组净发电功率相差较小，节能空间较小。

表4 不同环境温度范围每30 s的平均节电量

5 结 论

(1) 2018年7月得到的优化背压和优化机组净发电功率结果较为稳定，优化背压与实际背压差值基本在1 kPa以内，优化机组净发电功率与实际机组净发电功率差值稳定在10 MW以内。

(2) 机组在360～570 MW负荷段运行时的优化效果比在低负荷或者高负荷运行时好，调节最佳背压的优化空间较大。

(3) 机组在环境温度20～30 ℃运行时的优化效果较好，而在高温30 ℃以上运行时的优化效果较差，机组通过背压调节的节能空间较小。