电流是“通量”的理解与运用

鲁 斌 冯子江 向 豪

(浙江省余姚中学 浙江 宁波 315400)

在高中物理课堂中，“通量”的概念虽没有专门提及，但时常出现相关延伸的物理量.譬如在研究电磁感应时涉及的“磁通量”，研究电磁流量计时涉及的“水流量”等.其实“电流”也是“通量”，如果能够深刻领会电流是通量的内涵，对物理概念的理解大有裨益.

1 电流是通量

1.1 电流的定义

通常，我们把单位时间内通过导体任一横截面的电荷量叫做电流，简称电流.其定义式为

从定义上来说，电流的大小等于单位时间内通过某一截面的净电荷量.

1.2 通量的定义

在数学上[1]，我们用如下方法定义通量.如图1所示，假设有矢量场

Α(x,y,z)=P(x,y,z)i+

Q(x,y,z)j+R(x,y,z)k

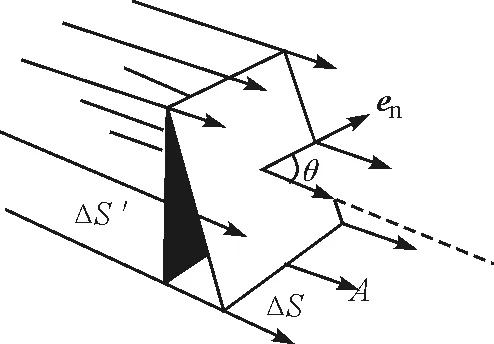
图1 A通过有向曲面

其中函数P,Q,R均具有一阶连续偏导数，S是场内的一片有向曲面，en是S在点(x，y，z)处的单位法向矢量，则积分

ΦA=∬SA·dSen=∬SA·dS

(1)

称为矢量场A通过曲面S向着指定侧的通量.将A与S在直角坐标系下表示，通量又可以表达为

ΦA=∬S1Pdydz+∬S2Qdzdx+∬S3Rdxdy

根据此定义方法，我们定义磁通量为

ΦB=∬SB·dS

表示穿过某一面积磁感线的条数.

定义电场强度通量为

ΦE=∬SE·dS

表示穿过某一面积电场线的条数.

定义水流量为

Φv=∬Sv·dS

表示穿过某一面积的水流线的条数.

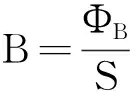
1.3 电流是通量

我们可以用相同的方法定义电流，使其与通量的定义式(1)保持一致.将A用j替代，则电流可定义为

I=∬Sj·dS

将上式取微分，有

dI=j·dS

可以看出，j在数值等于单位垂直面积上通过的电流.定义j为电流密度矢量[2]，即单位时间里通过单位垂直截面的电荷量.它的方向代表该点的电流方向.如图2，设想在导体中某点取一个截面元dS，它法线en与电流方向成倾斜角θ，则有

dI=jdScosθ

图2 电流密度

j与E具有相似的性质.在导体中各点的j有不同的数值和方向，这就构成一个矢量场，即电流场.电流场也可以用电流线(图3)来描绘.所谓电流线，就是这样一些曲线，其上每点的切线方向都和该点的电流密度矢量方向一致.电流线穿过截面的条数越多，电流就越大，反之亦然.由此可见，电流密度j和电流I的关系，就是一个矢量场和它的通量的关系.

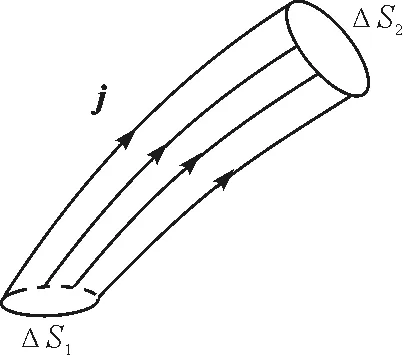
图3 电流线

2 关于电流是通量的理解

2.1 加速场中电流是通量的理解

如图4所示，在竖直线①左侧，假设每个小球的带电荷量为e，相距为l0，向右运动的速度为v0.

图4 初始状态

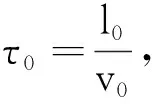
假设在通过直线①后，遇到向右的电场，带电粒子在电场中加速运动，经过t=τ0，2号粒子越过①进行加速，各粒子的状态如图5所示.

图5 2号粒子开始加速

经过t=2τ0，3号粒子越过①进行加速，粒子的运动如图6所示.

图6 3号粒子开始加速

如图7所示，当t=3τ0时，假设1号粒子正好通过直线②.由于1号和2号进入加速场的时间间隔为τ0.可以得到，再经过τ0，2号粒子通过直线②，再经过τ0，3号粒子也通过直线②.

图7 4号粒子开始加速

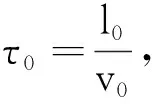
结果与未加速前是一样的.用电流的微观表达式I=nqvs来解释本场景，在加速过程中，v增大，但电荷线密度λ=nqs减小，导致最后电流值不变.

假设经过nτ0时间加速，1号粒子的速度为

v1=v0+anτ0

i号粒子的速度为

vi=v0+a(n-i+1)τ0

在i号粒子附近，还有i+1与i-1号粒子，它们之间的距离为

2[v0+a(n-i+1)τ0]τ0

则i号粒子附近的电荷线密度为

则，在i号粒子形成的电流为

虽然在加速过程中速度增大，但电荷之间距离拉大，电荷线密度减小，保证电流相等.从通量的角度来讲，无论粒子的速度为多大，间隔有多大，只要保证每经过τ0，就有一个粒子通过，那么电流的大小是一样的.

举一个生活中的例子，有一列汽车，在城市道路上两车间距离较近，运动速度较慢，在高速公路上两车间的距离较远，运动速度较快，但单位时间内通过的车辆数可能是一样的.这也是为什么城市限速低于高速公路限速的原因之一：在汽车“通量”一定的情况下，城市道路车流密度大时，运行的速度要低，高速公路车流密度较小时，运行的速度可以提高.

2.2 恒定电流中电流通量的理解

按照电荷守恒定律，电荷的代数和保持不变.在电流场中，任取一个闭合曲面S，所围的体积为V，则某段时间内流出曲面S的电荷量应当等于同一段时间内区域V中减少的电荷量.即有

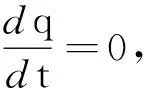
Sj·dS=0

(2)

这叫做电流的恒定条件.它表明，通过S面一侧流入的电荷量等于从另侧流出的电荷量，也就是说，任何时刻进入封闭曲面的电流线条数与穿出该封闭曲面的电流线条数相同，如图8所示.因此，恒定电流的电流线不可能在任何地方中断，它们永远是闭合曲线.

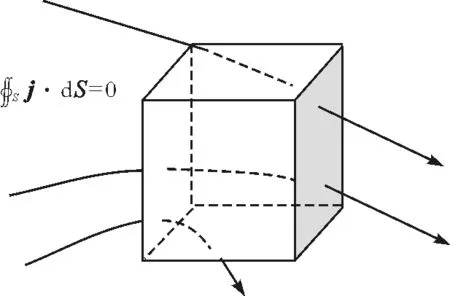
图8 电流连续原理

3 关于电流是通量的运用

3.1 基尔霍夫第一方程组

基尔霍夫第一方程组又称节点电流方程组：汇于节点的各支路电流的代数和为零，即

∑(±Ii)=0

节点电流方程是电流恒定条件的结果，也就是节点电流密度通量为零的结果.如图9所示，作闭合曲面S包围电路的节点，由于是恒定电流，根据公式(2)，流向节点的电流密度通量与从节点流出的电流密度通量的代数和应为零.即满足

Sj·dS=∬S1j1·dS1+∬S2j2·dS2+

∬S3j3·dS3=0

即有I1+I2+I3=0，即满足

即q内为一常数.此为电荷守恒定律，否则节点有电荷积累，破坏恒定条件.

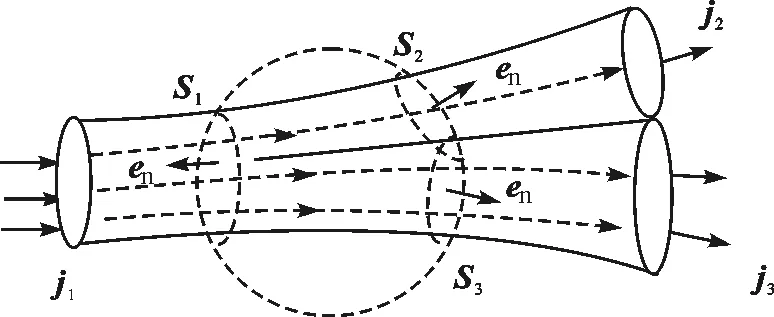
图9 电流节点定律示意图

3.2 光电效应的饱和电流

光电效应中，随着正向电压的增大，电流会趋于饱和.我们讨论两种情况.

(1)如果光电管的阴极为一小球(图10)，阳极为同心球，此时如果外界光源恒定，保证了单位时间内出射的电子数恒定，这个阳极的形状将光电子初速度角分布的因素排除了.

我们在光电管内取以阴极为中心的任意同心球面，通过他们的电流线的条数是一样的，即通过的电流密度的通量是一样的，即电流值保持不变，与加速电压无关.所有的光电子都能到达阳极，故在未加电压情形下，可以直接呈现饱和电流[3](图11).

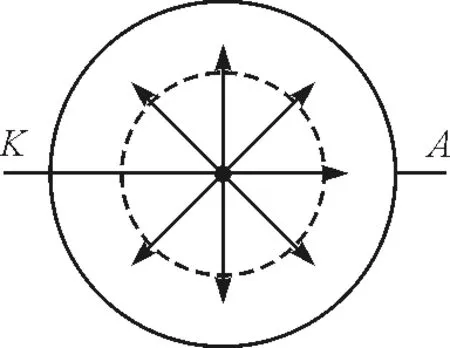
图10 光电管

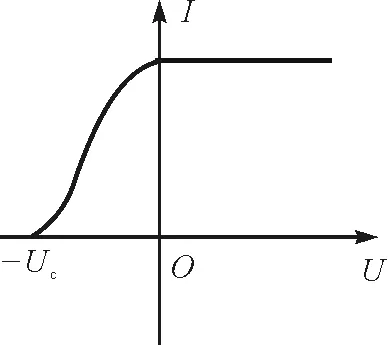
图11 伏安特性曲线

(2)如果光电管的阳极为平面(图12)，在单位时间内出射电子数恒定的情况下，由于光电子的角分布，则通过面①的电流通量与通过面②的电流密度通量不同，即阴极出射的光电子未能全部被阳极吸收，导致在此时未到达饱和.

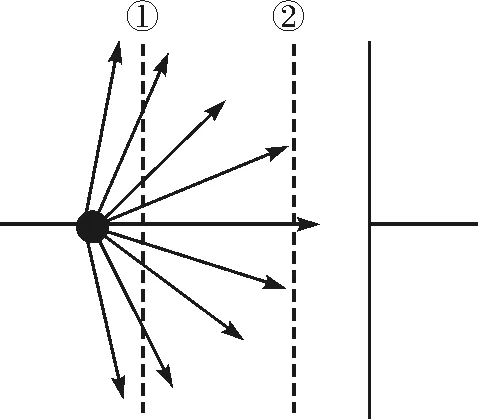
图12 光电管

随着加速电压的增大，电流线开始弯曲，电流场分布发生变化，直到所有光电子在电场作用下都到达阳极，此时，通过①与②的通量趋于一致(图13).

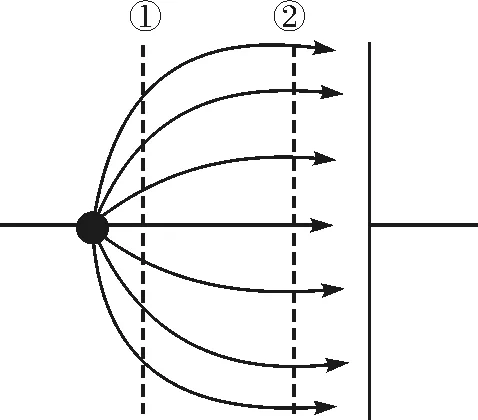
图13 趋于饱和

之后若继续增大电压，会影响电流线的分布(图14)，但不影响流经面②的通量.其伏安特性曲线如图15所示.

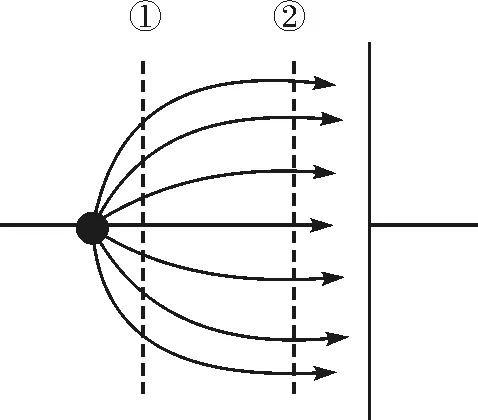
图14 饱和

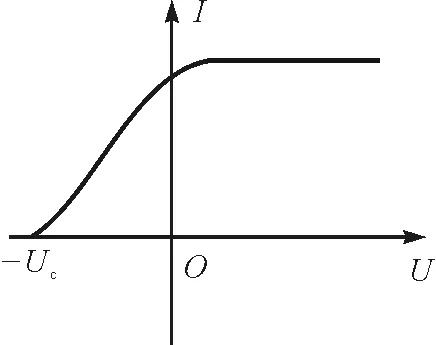
图15 伏安特性曲线

4 结束语

电流在本质上来说是电流密度的通量.由于数学结构相同，它表现出与电通量、磁通量等相似的性质.在教学过程中，应渗透“通量”的概念，理解“通量”的内涵，掌握“通量”的应用，可以更好地理解电流这个在中学物理中极其重要的物理量.