胶粉复合改性沥青混合料疲劳性能
殷卫永, 王笑风, 吴靖江, 郭永富, 张 永
(1.交通运输行业公路建设与养护技术、材料及装备研发中心,郑州 450000;2.河南省交通规划设计研究院股份有限公司,郑州 450000; 3.中国建筑第七工程局有限公司,郑州 450000)
胶粉复合改性沥青混合料可大量消耗废旧轮胎胶粉并改善混合料性能,具有重要推广价值[1-3]. 疲劳性能可反映路面通车服役状态下长期性能,对指导路面全寿命周期建设与养护具有重要意义[4-5]. 目前部分学者关于胶粉改性沥青混合料疲劳性能开展相关研究. 隆然和马启和[6]基于三分点加载试验分析了胶粉细度、用量和掺量对橡胶沥青混合料疲劳性能的影响;申爱琴等[7]以橡胶沥青混合料疲劳损伤曲线特征值为疲劳性能评价指标,建立BP神经网络全周期疲劳寿命预测模型;房辰泽[8]等建立了累积劲度模量衰减量相对变化率与疲劳荷载次数的函数关系式和损伤模型,并以此评价橡胶沥青混合料疲劳寿命;孙雅珍等[9]基于三点弯曲疲劳试验,采用耗散能相对变化率定义的损伤变量分析损伤演化过程,并建立耗散能相对变化率与疲劳寿命的相关关系以预测橡胶沥青混合料疲劳寿命. 综上可知,目前这些研究大多集中在疲劳寿命评价指标适用性分析及疲劳寿命预测. 实际使用过程中,疲劳性能受到温度和荷载水平等因素的综合影响[10-11],关于不同条件下胶粉改性沥青混合料疲劳寿命测试及分析仍需进一步深入研究.
沥青混合料作为不均匀性材料,室内试验测试的疲劳寿命往往离散性较大[12],甚至在试验条件完全相同的情况下,试验结果也会出现几倍偏差,采用简单比较或平均数方法直接比较会严重影响分析结果的准确性. 为此,部分学者将沥青混合料疲劳寿命视为随机变量,并采用概率统计理论描述,其中Weibull分布函数是常用的分布理论. 黄琴龙等[13]基于Weibull分布建立了乳化沥青水泥稳定碎石混合料的疲劳寿命预估模型;陈华梁等[14]研究发现盐-湿-热循环作用条件下沥青混合料疲劳性能服从Weibull分布;罗桑等[15]运用Weibull分布预测不同温度和应变水平下的环氧沥青混合料疲劳寿命. 采用Weibull分布理论分析疲劳寿命被证明切实有效[16-17].
基于此,该文研究胶粉复合改性沥青在不同温度和应变水平下疲劳寿命,并与SBS改性沥青混合料对比分析,研究两种类型沥青混合料疲劳寿命试验结果是否服从Weibull分布,并进一步探索采用Weibull分布理论分析试验结果,综合对比两种不同类型沥青混合料疲劳性能,以期为胶粉复合改性沥青的进一步推广应用提供参考.
1 原材料及试验方法
1.1 原材料
胶粉复合改性沥青为橡胶粉与SBS复合改性沥青,本研究中采用工厂化制备的成品胶粉复合改性沥青. 以基质沥青为基准外掺计算,胶粉掺量为20%,SBS掺量为2%,表面活性剂和交联剂掺量分别为0.7%和0.2%. SBS改性沥青采用中石油SBS改性沥青. 胶粉复合改性沥青和SBS改性沥青性能指标如表1所示.
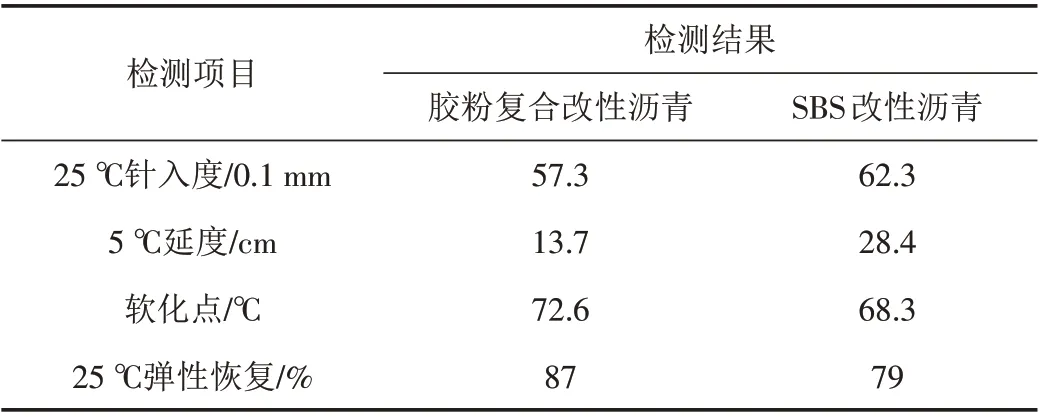
表1 改性沥青性能指标Tab.1 Performance indexes of modified asphalt
1.2 试验方法
1.2.1 成型试件 首先按照《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)中T0703 方法,采用轮碾法成型沥青混合料试块,但采用试验模具为专用特制模具,试模内部有效尺寸长、宽、高分别为400、300、75 mm. 然后将试块采用双面锯切割成380 mm×63.5 mm×50 mm的标准疲劳试验试件. 胶粉复合改性沥青混合料和SBS改性沥青混合料分别成型足够数量的疲劳试件. 测试每种类型混合料疲劳试件空隙率,实测空隙率须在目标空隙率±0.5%范围内,超出范围的试件应废弃.
1.2.2 试验仪器及试验条件 参照《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)中T0739沥青混合料四点弯曲疲劳寿命试验方法,试验仪器采用UTM-30,控制模式为应变控制,加载波形为haversine 偏正弦波,加载频率10 Hz,泊松比0.4,试验终止条件为弯曲劲度模量降低到初始弯曲劲度模量的50%. 试验温度选择10、20、30、40 ℃四个温度,每个温度下选择200、400、600 με三个应变水平. 试验前,每个被测试件需在设定温度下保温至少4 h. 每种类型沥青混合料在每个试验温度和应变水平下,分别进行三次平行试验. 试验仪器及试件如图1所示.

图1 疲劳试验仪器和试件Fig.1 Fatigue test instruments and specimens
2 试验结果分析
2.1 试验结果
不同测试温度和应变水平下,胶粉复合改性沥青混合料和SBS改性沥青混合料疲劳寿命试验结果如表2.
由表2分析可知,不同温度和应变水平下,胶粉复合改性沥青和SBS 改性沥青每组平行试验内,不同试件疲劳寿命测试结果差异较大. 在相同应变水平和温度下,胶粉改性沥青和SBS 改性沥青混合料疲劳寿命互有大小,试验结果离散性较大,简单比较几个数据不能较好地评价两种不同类型沥青混合料疲劳性能优劣,直接采用平均数方法亦会产生较大试验结果偏差,严重影响结果评价的真实准确性. 因此,需进一步应用合适的统计分析理论对疲劳寿命数据深入分析.
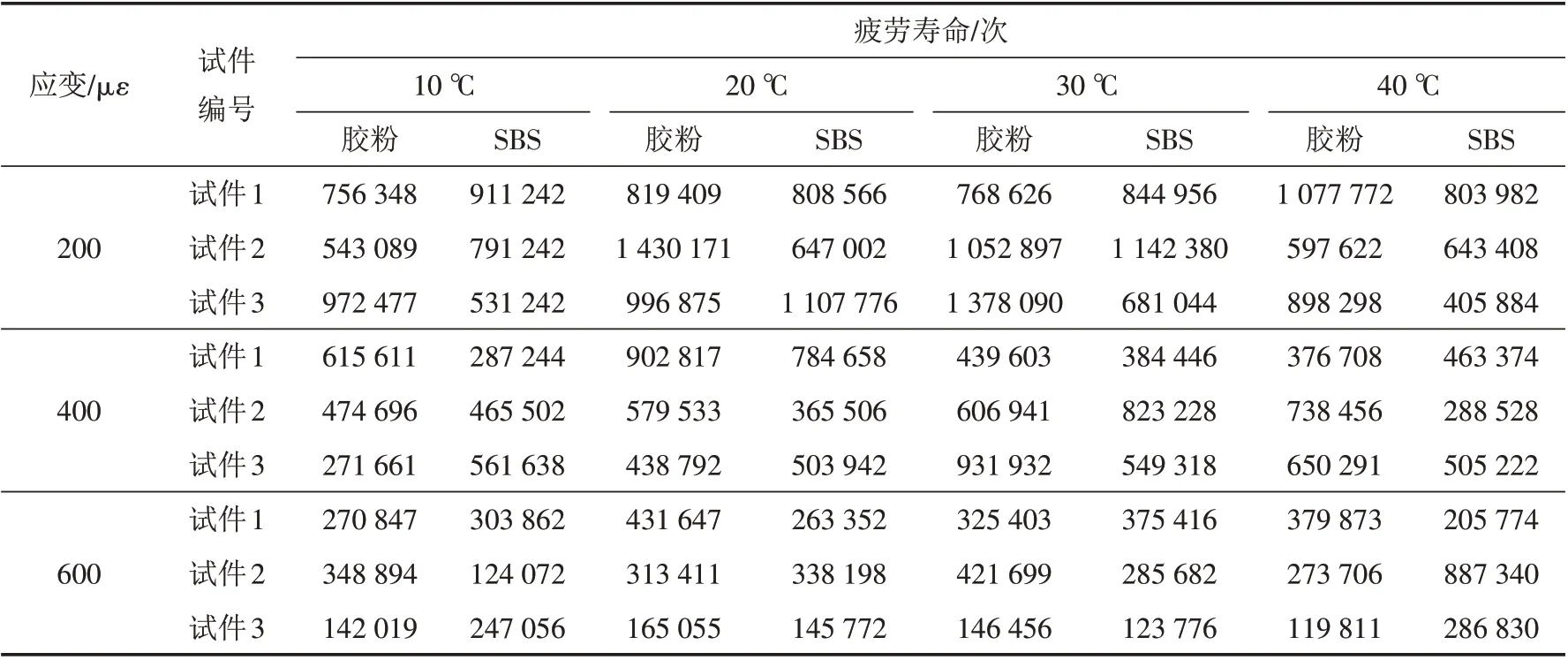
表2 不同条件下改性沥青混合料疲劳寿命Tab.2 Fatigue lifetimes of modified asphalt mixtures under different conditions
2.2 Weibull分布函数
针对沥青混合料疲劳寿命试验结果偏差较大的特征,可将疲劳寿命看作随机变量,采用概率统计理论对试验结果进行系统分析. Weibull分布是疲劳寿命分析中常用的分布函数,目前研究中大多数采用的是双参数Weibull分布,即假定位置参数N0=0,疲劳失效寿命从0开始计数,这与沥青混合料实际疲劳破坏演变规律不符合[18]. 三参数Weibull分布更符合实际,其概率密度如公式(1)所示,分布函数如公式(2)所示.

式中:b为形状参数;Na为特征疲劳寿命,等同于36.8%保证率的安全寿命;N0为位置参数,即最小疲劳寿命参数.
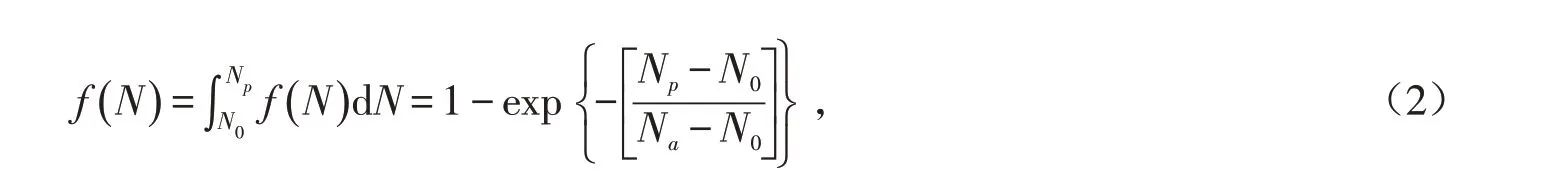
式中:Np为保证率为p时的疲劳寿命. 将公式(2)两边取自然对数,并运用换底公式得到公式(3).
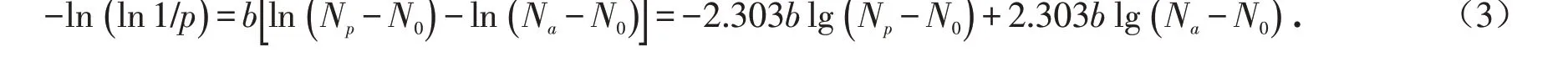
由公式(3)可知,若疲劳寿命试验结果服从Weibull分布,则-ln( ln 1/p)与lg(Np-N0)两者之间存在良好的线性关系. 因此,可根据两者是否存在线性关系,判断疲劳寿命试验结果是否服从Weibull分布,同时计算特定失效概率(保证率)下疲劳寿命预估量.
2.3 不同条件下疲劳寿命Weibull分布函数检验

图2 胶粉改性沥青混合料疲劳试验结果Weibull分布检验回归图Fig.2 Regression diagrams of Weibull distribution tests for fatigue lifetimes of crumb rubber modified asphalt mixtures

图3 SBS改性沥青混合料疲劳试验结果Weibull分布检验回归图Fig.3 Regression diagrams of Weibull distribution tests for fatigue lifetimes of SBS modified asphalt mixtures

2.4 基于Weibull分布函数的疲劳寿命分析
由于不同温度和应变下胶粉改性沥青和SBS改性沥青疲劳寿命均服从Weibull分布,可根据表4中不同温度和应变水平下疲劳寿命与保证率回归方程,计算不同保证率下的疲劳寿命[21]. 分别令p=95%和50%,算出95%和50%保证率时,不同温度和应变下胶粉改性沥青和SBS改性沥青疲劳寿命,如图4所示.

图4 不同保证率下沥青混合料疲劳寿命Fig.4 Fatigue lifetimes of asphalt mixtures with different guarantee rates

表4 SBS改性沥青混合料疲劳寿命Weibull分布检验回归方程Tab.4 Regression equations of Weibull distribution tests for fatigue lifetimes of SBS modified asphalt mixtures
根据图4分析不同类型沥青混合料疲劳寿命随温变化规律. 95%保证率时,不同应变水平下,测试温度由10 ℃增加到40 ℃,胶粉改性沥青和SBS改性沥青疲劳寿命先升高后降低. 200 με下,胶粉改性沥青混合料疲劳寿命10 ℃时最低,20 ℃和30 ℃下基本相当且达到峰值,随后40 ℃时降低,降幅约为峰值的26%;SBS改性沥青混合料疲劳寿命从10 ℃到30 ℃逐渐增大,30 ℃达到峰值,40 ℃时显著降低,降幅约为峰值时的53%.400 με下,两种类型沥青混合料疲劳寿命从10 ℃到30 ℃逐渐增大,30 ℃达到峰值,40 ℃时疲劳寿命小幅降低,胶粉改性沥青混合料降幅约为峰值的11%,SBS改性沥青混合料降幅约为峰值的10%. 600 με下,两种类型沥青混合料疲劳寿命均在20 ℃下达到峰值,随后逐渐降低;40 ℃胶粉改性沥青混合料疲劳寿命降低幅度约为峰值的46%,SBS改性沥青混合料疲劳寿命降低幅度约为峰值62%. 50%保证率时,不同温度下两种类型沥青混合料疲劳寿命变化规律类似于95%保证率时变化规律.
相同温度下,对比两种类型沥青混合料疲劳寿命. 95%保证率时,10 ℃条件下,200 με和600 με时,胶粉改性沥青混合料疲劳寿命与SBS改性沥青混合料基本相当;400 με时,胶粉改性沥青混合料疲劳寿命略低于SBS改性沥青混合料. 20、30、40 ℃条件下,200 με和400 με时,胶粉改性沥青混合料疲劳寿命均高于SBS改性沥青混合料,600 με时两者疲劳寿命基本相当. 20 ℃条件下,200、400、600 με时,胶粉改性沥青混合料疲劳寿命分别是SBS改性沥青混合料的1.18、1.24、0.98倍;30 ℃条件下,对应的倍数分别为1.06、1.14、1.27倍;40 ℃条件下,对应的倍数分别为1.68、1.12、1.39倍. 50%保证率时,不同温度和应变水平下,两种类型沥青混合料疲劳寿命对比规律与95%保证率时整体一致,个别点存在约10%~20%偏差.
不同应变水平下,两种不同类型沥青混合料疲劳寿命在10 ℃时均较低,在20 ℃或30 ℃下均达到峰值,40 ℃下疲劳寿命降低,表明低温和高温环境均会降低混合料疲劳寿命. 40 ℃下200 με和600 με时,胶粉改性沥青混合料疲劳寿命降低幅度显著低于SBS 改性沥青混合料,400 με时两者降低幅度基本相当.20~40 ℃下,相同温度时,胶粉改性沥青混合料疲劳寿命整体高于SBS改性沥青混合料;温度越高,胶粉改性沥青混合料相对SBS改性沥青的疲劳寿命越高. 表明胶粉改性沥青混合料耐疲劳性能优于SBS改性沥青混合料,尤其在较高温度下,胶粉改性沥青混合料耐疲劳性能更具优势.
2.5 基于Weibull分布函数的疲劳方程分析
结合2.4节中不同温度和应变水平下疲劳寿命,在不同温度下,分析疲劳寿命与应变水平之间的相关关系,建立关于疲劳寿命与应变水平的疲劳方程,分析不同温度下不同类型沥青混合料疲劳方程特征,从而对比评价不同类型沥青混合料耐疲劳性能. 不同保证率和温度下,两种类型沥青混合料疲劳寿命与应变水平之间的疲劳方程如表5所示.
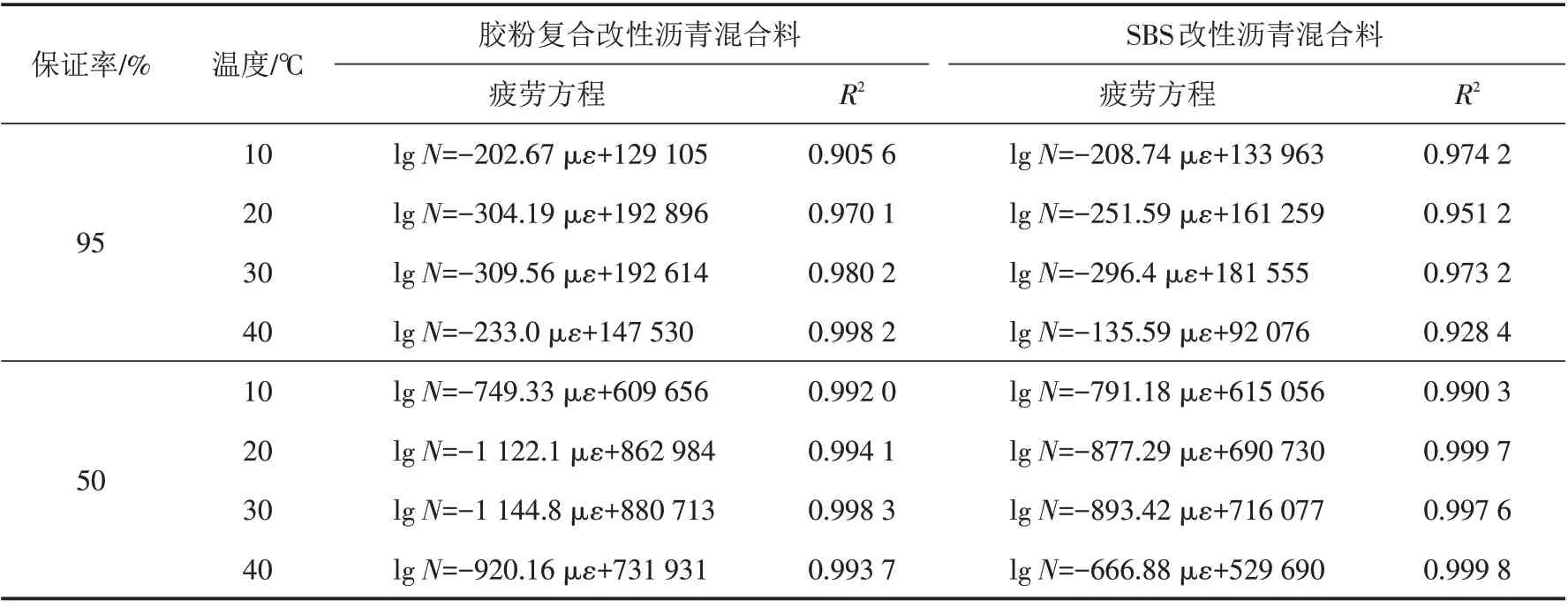
表5 不同类型沥青混合料疲劳方程Tab.5 Fatigue equations of different types of asphalt mixtures
由表5分析可知,两种类型沥青混合料在不同温度下,疲劳寿命与应变水平之间均具有良好的线性相关关系,相关系数均在90%以上. 线性疲劳方程的截距反映了疲劳曲线的高低,代表了混合料耐疲劳性能的优劣;截距越大代表混合料耐疲劳性能越好. 线性疲劳方程的斜率绝对值大小反映了疲劳曲线陡缓程度,代表了混合料对应变水平变化的敏感程度;斜率绝对值越大,疲劳曲线越陡,表明混合料对应变水平变化越敏感.
在95%保证率下,胶粉复合改性沥青混合料疲劳方程截距与SBS 改性沥青混合料疲劳方程截距相比,10、20、30、40 ℃时,前者分别约为后者的0.96、1.2、1.06、1.6倍. 50%保证率下,对应的倍数分别为0.99、1.25、1.23、1.38倍. 在95%保证率下,胶粉复合改性沥青混合料疲劳方程斜率与SBS改性沥青混合料疲劳方程斜率相比,10 ℃和30 ℃时两者基本相当,20 ℃和40 ℃时前者约为后者的1.21、1.72 倍;50%保证率下,10、20、30、40 ℃时,对应的倍数分别为0.94、1.27、1.28、1.38倍.
疲劳方程的截距和斜率分析表明,胶粉复合改性沥青混合料耐疲劳性能总体优于SBS改性沥青混合料,高温下疲劳性能变化幅度较小. 胶粉复合改性沥青中胶粉改善了沥青及混合料耐高温性能及温度敏感性,提高了高温下抗变形和耐疲劳性能. 虽然胶粉复合改性沥青对应变水平敏感性亦大于SBS 改性沥青混合料,但不同应变水平下耐疲劳性能仍整体优于SBS改性沥青混合料. 胶粉复合改性沥青对应变水平的敏感性可能与胶粉掺量及制备工艺、测试条件等因素有关,其更深层影响关系值得后续进一步深入研究.
3 结论
通过上述胶粉复合改性沥青混合料及SBS改性沥青混合料疲劳性能测试及分析,可得出以下结论:
1)胶粉复合改性沥青混合料和SBS改性沥青混合料疲劳寿命试验结果存在较大离散性,简单对比或直接取平均数存在较大偏差.
2)胶粉复合改性沥青混合料和SBS改性沥青混合料疲劳寿命回归分析表明-ln( l n 1/p)与lg(Np-N0)两者具有良好的线性关系,相关系数在0.9以上,两种类型沥青混合料疲劳寿命均服从三参数Weibull分布.
3)从10 ℃到40 ℃,胶粉复合改性沥青混合料和SBS 改性沥青混合料疲劳寿命先升高后降低,两者在20 ℃和30 ℃下基本相当且达到峰值,40 ℃时前者降低幅度显著低于后者.
4)20~40 ℃时,相同温度和应变条件下,胶粉复合改性沥青混合料疲劳寿命均高于SBS 改性沥青混合料,尤其在40 ℃条件下前者更具优势.
5)胶粉复合改性沥青混合料和SBS改性沥青混合料疲劳寿命与应变水平可用线性回归疲劳方程表示.疲劳方程的截距分析表明,胶粉复合改性沥青混合料耐疲劳性能优于SBS改性沥青混合料,高温下疲劳性能变化幅度较小.

