基于改进隐马尔可夫模型的云网络安全研究

郑友生

(泉州幼儿师范高等专科学校 信息教育技术中心，福建 泉州 362000)

在云计算和大数据高速发展的今天，信息安全、云平台防护等面临巨大威胁，如病毒入侵、DDoS攻击、黑客攻击等。从当前网络面临的威胁来看，传统的IDS、IPS等被动防御已不能满足网络安全防护需求，必须加强网络安全态势感知。在网络安全态势感知中，主要数据来源于日志文件、网络设备等。通过对这些数据的整合、关联分析，并结合态势评估算法，实现态势预测评估目的，以争取在网络攻击前规避或者是遏制部分威胁，达到保护和降低攻击的目的。而当前基于网络安全态势的评估中，比较常见的态势评估方法包括D-S证据理论[1]、朴素贝叶斯分类[2]、攻击图[3]、BP神经网络[4-5]等。李欣[8]将隐马尔可夫模型(Hidden Markov Model, HMM) 应用到云网络环境中，认为隐马尔可夫模型在实时评估网络状态方面具有无可比拟的优势，但存在模型参数匹配较难、评估准确率不高的问题。基于以上研究理论和实践，提出一种自适应聚群粒子群算法的HMM参数优化方法，以此对云网络安全态势进行评估。

1 隐马尔可夫模型描述与改进

1.1 隐马尔可夫模型的数学描述

韩晓露[6]、王彩玲[7]等认为，网络的安全状态与实际观察的安全事件并非一一对应，而是通过概率分布产生联系，即网络安全的序列可展示网络状态的变化。在云网络中，将云网络看成是由若干个节点过程。网络攻击者通过网络节点发起攻击，因此对云网络安全的评估，可看成是对节点的安全态势评估，其中通过设备可搜集到节点的漏洞、病毒和攻击信息，是观测序列。为度量节点的安全状态，认为节点的安全状态与攻击者间是概率关系，可通过HMM来进行描述。通过HMM模型在对网络中的节点进行态势分量建模后，则通过出现最高概率的隐藏状态序列来进行安全态势的评估与判断。基于HMM的网络安全态势评估由五元组λ={S,M,π,A,B}构成，其中π和A为马尔科夫链参数，B表示一般随机过程的参数。根据周期内检测到的观测状态序列O={o1,o2,…,ot,…,oT}，可计算出各节点在t时刻的概率rt(i)。

(1)

为更好的度量节点安全态势，引入节点权重对态势进行评估，具体计算公式为：

(2)

式中，Z表示网络节点数目；SA表示网络安全态势值；WHi表示各个节点的权重。其中，应用pagerank算法对节点权重分配。具体分配公式为：

(3)

式中，a=0.85，w(hi)表示节点权重值，N表示网络中节点数目，Out(hj)表示hj的出链数目，Mpi表示hj的出链集合。

1.2 隐马尔可夫模型参数优化

在实际应用场景中，HMM模型参数设置暴露出人工设置的不准确性。因此，有必要对HMM参数进行优化，减少传统参数设置存在主观性过大的问题。针对该问题，李欣提出通过Baum- Welch(BW) 参数优化算法与人群搜索算法结合对HMM进行优化，结果表明该方法可提高准确率[8]。参考韩爱平[9]的研究成果，提出采用ASPSO对HMM参数进行优化。

传统的粒子群算法(PSO)虽然寻优速度快，可应用于HMM模型参数进行确定，但由于其构造简单，在搜索过程中容易陷入局部最优解，且收敛速度普遍较慢，因此需要对PSO算法进行改进。在该改进中，引入人工鱼群的拥挤度因子，进而避免传统PSO算法在HMM参数优化中容易陷入局部极值，从而达到全局最优的目的。

在引入人工鱼群算法的同时，对PSO算法也进行改进。具体则是对惯性权值ω和学习因子c1和c2的改进。对此，本文首先确定PSO算法的惯性权值ω在0.4～0.9。而在搜索迭代初期，通常取较大惯性权值，从而让粒子摆脱剧组最优，提高全局最优。而在后期，则取较小的惯性权值。因此，基于以上的分析，在本文中将算法的迭代代数 gen 自适应的惯性权值公式变为：

(4)

式中，gen表示迭代代数，genmax表示最大迭数，ωgen表示迭代代数gen的自适应惯性权值，ωmax=0.9，ωmin=0.4。

同时，PSO算法中初次迭代时，c1和c2会影响算法的全局寻优能力和收敛速度。为保证PSO就有较强的全局寻优和收敛速度，本文应用迭代代数gen与学习因子的关系，确定了C1、C2的更新公式：

(5)

c1=4-c2

(6)

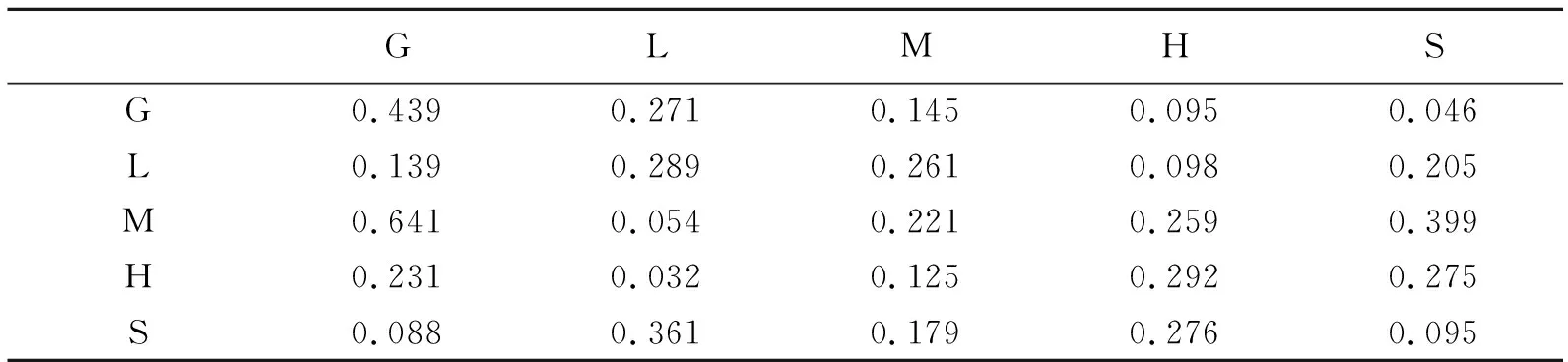
式中，gen表示迭代代数，genmax表示最大迭代代数，cmin表示学习因子c1的初始值，cmax表示学习因子c1的最终值，且满足0

2 基于ASPSO的隐马尔可夫模型的网络安全态势评估

结合以上对隐马尔可夫模型的改进，将云网络的安全态势评估步骤分为以下几步：

(1)确定HMM模型初始结构参数，包括状态转移矩阵和符号矩阵参数的确定；

(2)初始化种群，设定初始粒子群数目为50，最大迭代数为100，并确定种群中粒子的初始位置和初始速度，应用惯性权值计算公式(4)和学习因子计算公式(5)、(6)确定w和c1、c2的值；

(3)确定人工鱼群算法参数，设人工鱼总数为50，移动步长为0.5，最大试探数为4，拥挤度因子为0.2；

(4)计算粒子的适应度函数并更新其最优值；

(5)若迭代代数达到设定的最大迭代代数，停止算法，输出最优粒子个体；若迭代数没有达到最大迭代数，重复步骤(4)、(5)，直至得到最优参数；

(6)根据公式 (2)计算网络安全态势结果，并输出结果。

3 仿真实验

3.1 实验数据介绍

为研究改进HMM模型在云网络安全态势评估的可行性和优劣，以DARPA2000数据集为基础，模拟DDoS 攻击场景对云网络安全态势进行评估。DDoS 攻击网络流量主要分为五个阶段：

第一阶段：扫描活跃主机。IP为202. 77. 162. 213的攻击者对172. 16. 112. 0/24、172. 16. 113. 0/24、172. 16. 114. 0/24和 172. 16. 115. 0/24四个IP进行扫描，查询其中活跃的主机；

第二阶段：sadmind查询。查询活跃主机是否运行sadmind，若主机正在运行sadmind，可以 进 行 第 三阶段；

第三阶段：获取主机root权限。根据Sadmind Buffer Overflow漏洞获得172.16.112. 20、172.16.112.10、172.16.115. 50主机root 权限；

第四阶段：安装DDoS攻击工具。在172.16.112.20、172.16.112.10、172.16.115.50三台主机中安装DDoS攻击工具；

第五阶段：发起攻击。利用DDoS攻击工具发起攻击，远程控制172.16.112.20、172.16.112.10、172.16.115.50三台主机。

3.2 模型参数确定

为确保仿真实验的准确性，本文在Windows7操作系统、MATLAB2014b、硬件处理系统为500HZ、内存为512M以上的环境下进行实验。

设置 A B 的参数。π=(1，0，0，0，0)。应用MATLAB2017b软件多次对模型参数进行实验，最终确定模型的关键参数：惯性权值ωmax=0.9，ωmin=0.4；学习因子c1最大4，最小1；人工鱼群数最少50；人工鱼移动步长为0.5，最大试探数为4，感知距离为6，拥挤度因子为0.2。

3.3 仿真结果

3.3.1 迭代次数优化 通过以上设置，分别得到只采用PSO算法和应用ASPSO算法对HMM参数进行优化的结果，具体如图1和图2所示。

由图可知，PSO 算法对HMM模型参数的优化需要进行430次迭代才能得到最优解，而ASPSO算法对HMM模型参数的优化仅在第160代迭代数就可得到最优解，可见ASPSO算法的优化结果比PSO算法的优化结果显著。

3.3.2 参数优化结果 应用ASPSO对模型的状态转移矩阵参数和观测符号矩阵参数进行优化，可得到如下表1所示的状态转移矩阵参数，表2所示的观测符号矩阵参数值。

表1 状态转移矩阵A的参数

表2 观测符号矩阵B的参数

3.3.3 安全态势评估 采用DDOS攻击场景1对云网络进行攻击模拟，对云网络中的主机发起攻击。攻击发生的大致时间为：第一阶段18～30 min；第二阶段36～50 min；第三阶段62～63 min；第四阶段80min后；第五阶段118min 后。根据上述的模拟攻击，得到图3的安全态势评估结果和图4的安全态势评估曲线。

由图3可知，主机在被攻击者攻击时与实际攻击场合吻合，共经历五个阶段。当攻击者攻击进行到第三阶段时，由于主机安装有DDoS程序，因此后两个攻击阶段的态势曲线并没有通过曲线图反映出来。由图4可知，在攻击者攻击主机的第一阶段扫描过程中，云网络的态势值不高，为0.921；第二阶段sadmind扫描，网络的态势值开始增大，为1.866；第三阶段入侵成功，网络态势值达到3.935；第四阶段攻击过程中，网络的态势值不断减小直至趋于0；第五阶段控制主机，此时的网络态势值达到4.247。

由此，通过以上的研究，可以得出在不同阶段的网络安全态势，大大提高了对云网络安全的主动防御程度，为后续的网络主动防御提供了更多可借鉴的参数。

4 结语

通过ASPSO对HMM的优化看出，ASPSO可大大减少HMM寻优的迭代次数，从而在最少的迭代次数内得到最优适应度值。而通过优化后的HMM安全态势评估看出，评估结果与实际的攻击大致相同，说明本研究的改进有效，与实际的网络攻击接近，且可显示不同阶段的网络安全态势值，可作为对网络安全态势有效评估的手段。