合肥市房价影响因素及预测

吴新雄，鞠鹏飞，吴健茹

(1.马来亚大学 高等研究院，马来西亚 吉隆坡 50603 ；2.中国人民解放军92228部队，北京 100049；3.空军预警学院 科研学术处，湖北 武汉 430019)

2020年5月29日，第一财经新一线城市研究所发布《2020城市商业魅力排行榜》，合肥位列新一线城市名单。作为新晋一线城市之一，合肥市的上升驱动力主要来自于各项商业资源集聚度指标的提升以及城市人展现出的活力，而房地产行业则是商业资源集聚度的重要考量指标。本文将依据近二十年文献资料归纳房价影响因素，并考虑2010年后合肥市人民政府开始实施的房地产限购政策，依据2010年至2018年各年《合肥市统计年鉴》，研究晋升新一线城市后合肥市房价的发展并进行预测。

1 合肥市房价影响因素分析

1.1 影响因素的选取及基本特征

2010年以来，合肥市的市场经济取得了毋庸置疑的发展。城市的高速发展，随之而来的便是房价的上涨。据合肥市统计年鉴数据，2010年至2018年合肥市房价(元/m2)的增幅超过100%，具体涨幅趋势见图1。

为分析合肥市房价的影响因素，基于评价指标的代表性程度和可数字化的特点，本文选取合肥市房价(元/m2)作为观察变量，在先前学者研究文献的基础上将合肥市国内生产总值GDP(亿元)、人口数Pop(万人)、第三产业房地产业TIRE(亿元)、居民人均可支配收入PCDI(元)、城市化率UR、居民消费价格指数CPI、房地产开发投资额REINV(亿元)、销售面积SR(万m2)选取为合肥市房价影响因素指标，指标解释及来源见表1，2010～2018年影响因素原始数据见表2。

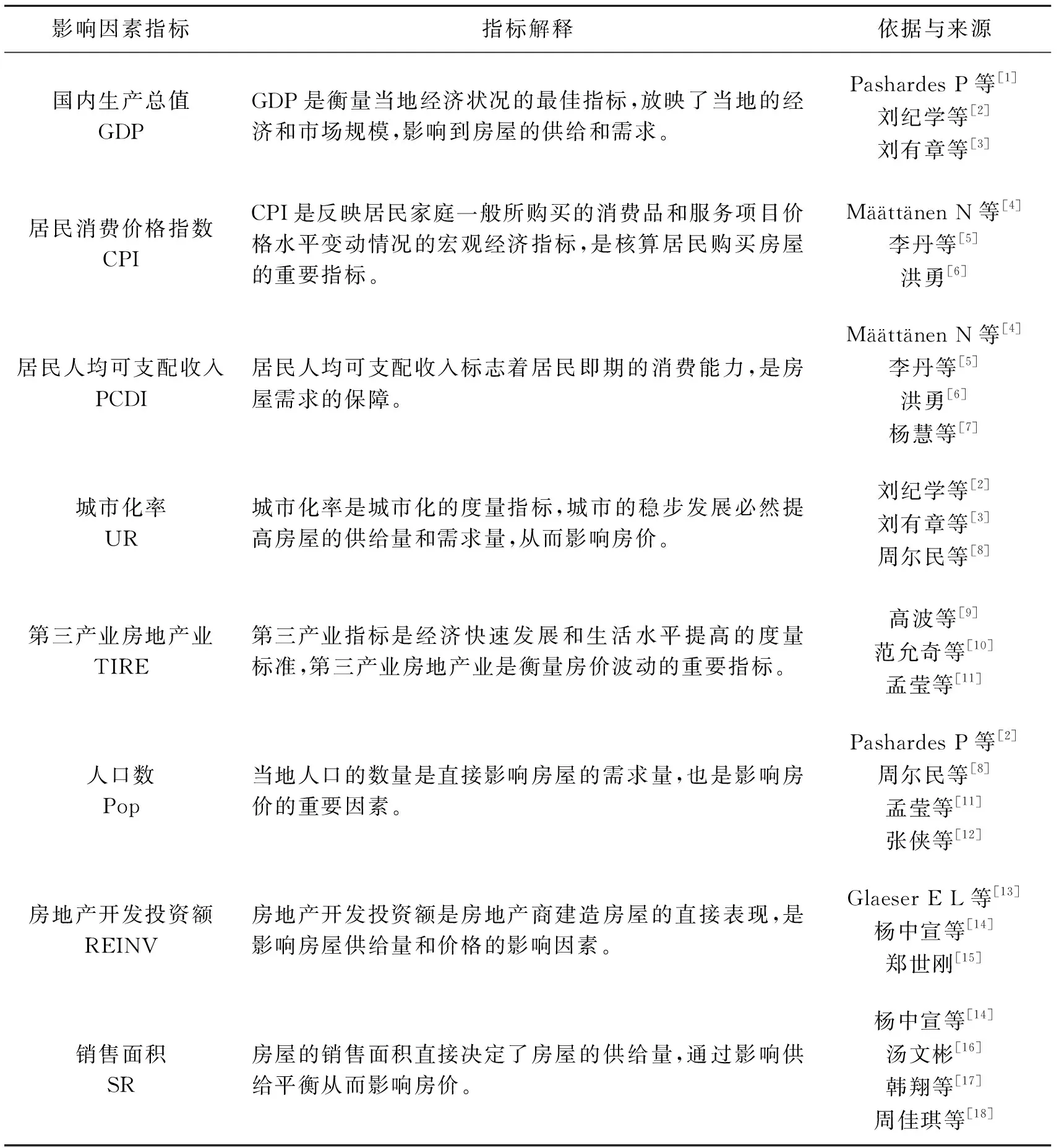
表1 合肥市房价影响因素指标解释及依据

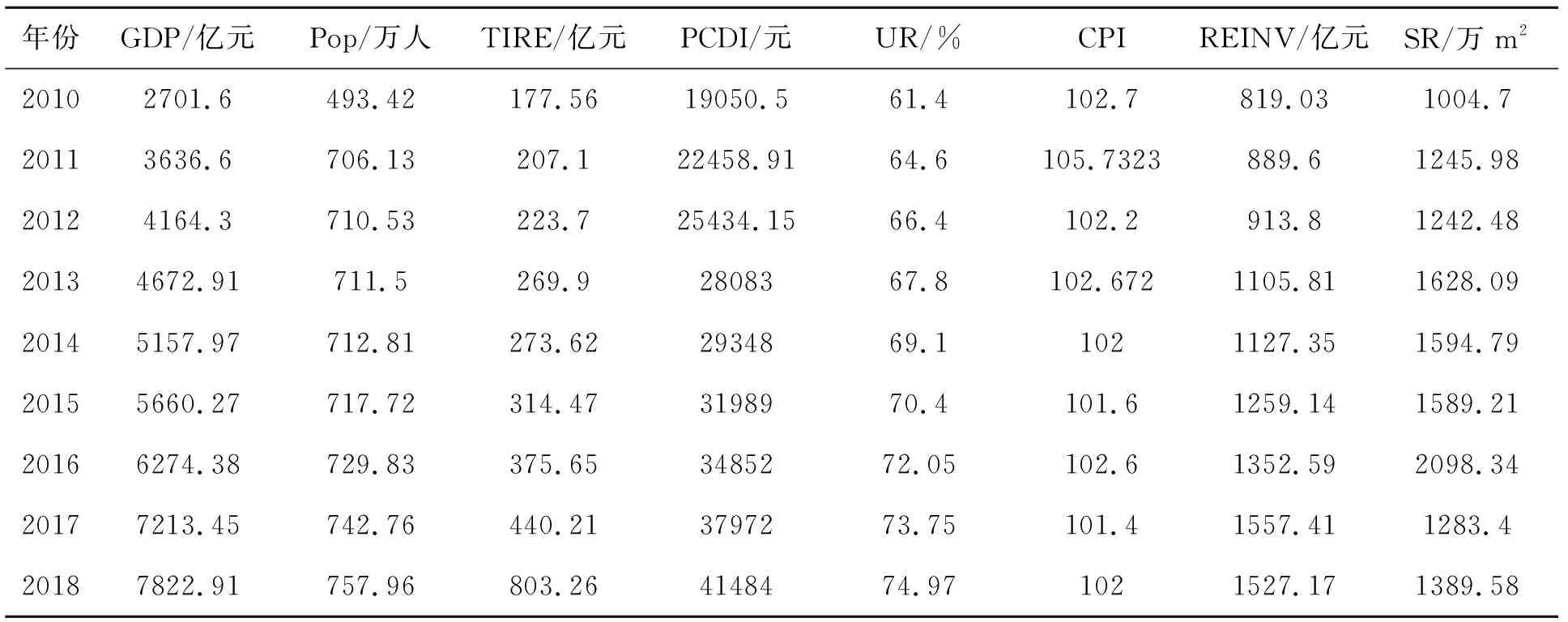
表2 2010～2018年房价影响因素原始数据

1.2 影响因素主成分分析

主成分分析(Principal Component Analysis，PCA)是一种统计方法。将一组可能存在相关性的变量通过正交变换转换成一组线性不相关的变量，转换后的这组变量就叫主成分。这种方法是通过数据降维的方式把较复杂的多组数据变量指标整合成少数几个综合指标，这样既减少了需要比较的指标个数，保证了数据的统一性，又确保了数据的解释程度。

为保证回归结果的准确程度，避免严重的多重共线性导致回归结果产生严重的误差，需要先对数据进行相关性检验，结果见表3。由表3可知，评价指标之间存在明显的相关性，为消除相关性带来的误差，本文采取主成分分析法，对影响因素成分进行提取并回归。

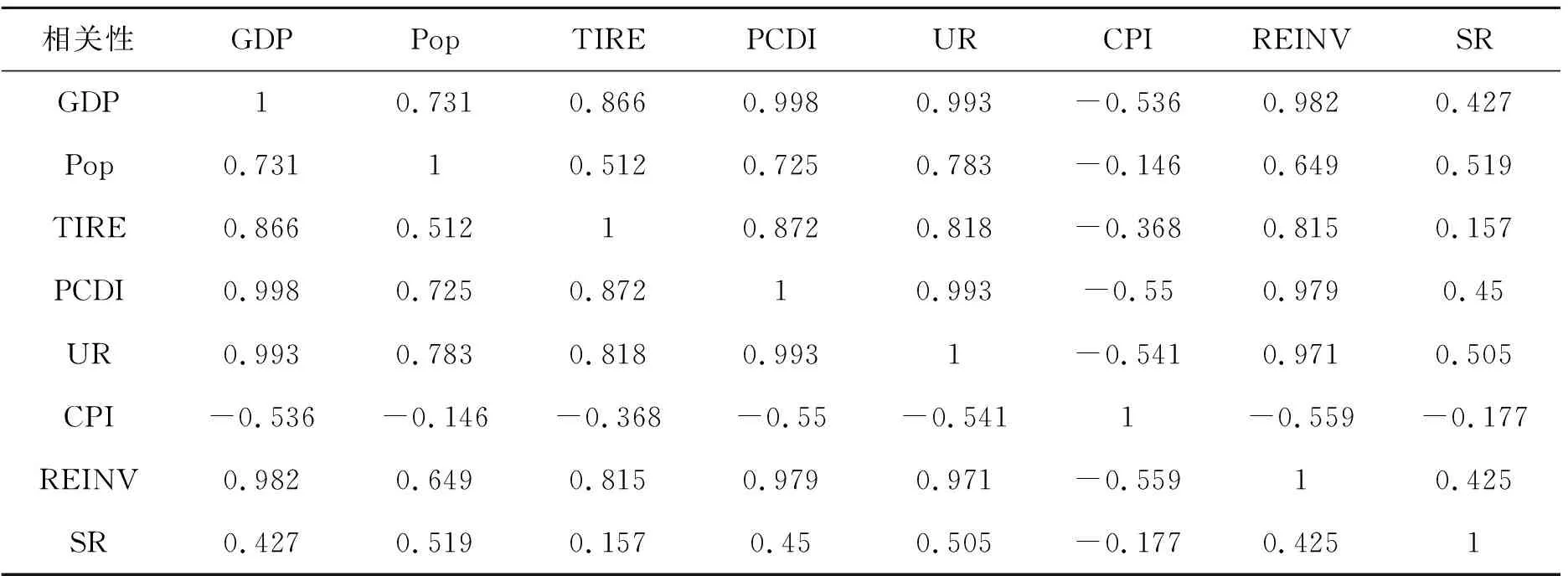
表3 影响因素相关性系数矩阵

在运用主成分分析法前，需要对原始数据进行KMO和巴特利特球形检验。KMO检验统计量是用于比较变量间简单相关系数和偏相关系数的指标，大于0.5表示可以接受。巴特利特球形检验的原假设是相关系数矩阵为单位阵，实验结果显著性小于0.01，拒绝原假设，认为相关系数矩阵不为单位阵，说明原变量间存在相关关系，适合做主成分分析。实验结果见表4。

表4 KMO和巴特利特球形检验结果

运用SPSS 22.0软件对数据进行主成分分析方法提取，总方差解释结果见表5。其中第一、第二成分的初始特征值为5.771和1.034，解释方差百分比为72.14%和12.925%，累计解释方差百分比达到85.065%，表明这两个成分可以综合表达各影响因素解释变量，且数据流失程度很小，具有高水平的代表性，故提取这两个成分作为反映合肥市房价影响因素的主成分。碎石图(图2)中转折点与陡峭程度也体现了两个成分的表达水平，主成分1和2分别记为Z1、Z2。

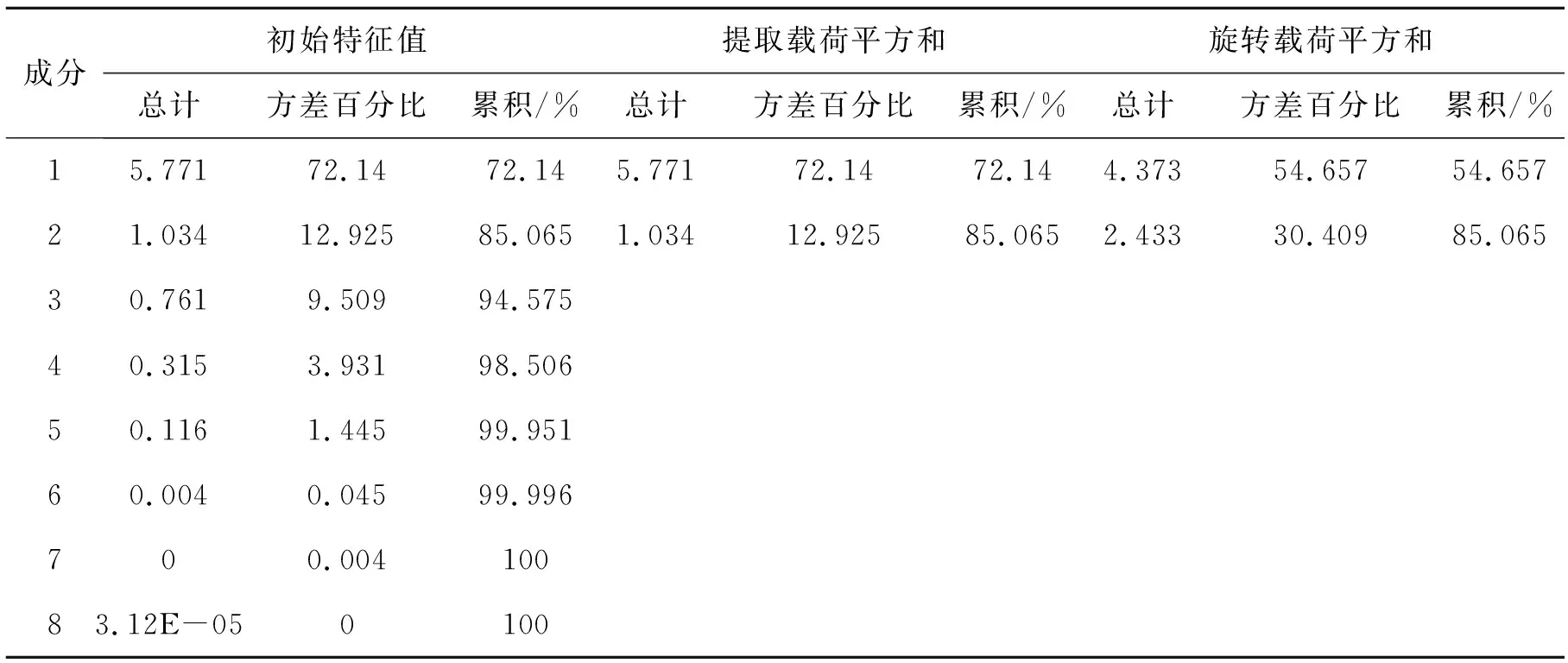
表5 总方差解释表

运用主成分分析法对数据提取了两个成分后，成分矩阵见表6。对成分矩阵运用凯撒正态化最大方差法进行旋转，旋转三次迭代后已收敛，旋转后的成分矩阵见表7。

表6 成分矩阵 表7 旋转后的成分矩阵

基于旋转后的成分矩阵，成分得分系数矩阵见表8。

表8 成分得分系数矩阵

房价影响因素指标主成分数学模型为：

Z1=0.178×GDP-0.13×Pop+0.263×TIRE+0.176×PCDI+0.132×UR-0.347×CPI+0.193×REINV-0.291×SR

Z2=0.042×GDP+0.444×Pop-0.138×TIRE+0.046×PCDI+0.114×UR+0.357×CPI+0.011×REINV+0.61×SR

1.3 回归分析

利用最小二乘法对房价和主成分Z1、Z2进行回归分析，线性回归方程为：

ZY=7976.511+0.882×Z1+0.3×Z2

(t=5.933)(t=2.021)

上述方程中ZY表示标准化后合肥市房价的数值，参数对应的t统计量均大于1.96，可决定系数R2为0.867，F统计量为19.641，表明该模型拟合程度良好，数据可靠性高，显著程度明显，主成分Z1、Z2是合肥市房价的重要影响因素。根据标准化系数及回归方程，最终计算得到方程：

Y=0.1695×GDP+0.01854×Pop+0.190566×TIRE+0.169032×PCDI+1.0482×UR-0.198954×CPI+0.173526×REINV-0.07362×SR+7976.511

由回归方程可知，影响因素指标对合肥市房价影响程度大小排序依次为：城市化率、居民消费价格指数、第三产业房地产业、房地产开发投资额、地区国民生产总值、城镇居民可支配收入、销售面积和人口数。

2 合肥市房价预测

灰色预测模型是对原始数据进行累加生成，弱化原始时间序列数据的随机因素，然后建立生成数的微分方程。GM(1，1)模型是灰色系统理论中的单序列一阶灰色微分方程，本文将基于该模型对合肥市房价进行预测。

2.1 运算过程

设已知序列为X(0)(1)，X(0)(2)，…，X(0)(n)，做一次累加AGO(Accumulated Generating Operation)生成新序列：

X(0)=(X(0)(1),X(0)(2),…,X(0)(n))

其中X(1)(1)=X(0)(1)，X(1)(2)=X(1)(1)+X(0)(2)，…，X(1)(n)=X(1)(n-1)+X(0)(n)

生成均值序列：Z(1)(k)=aX(1)(k)+(1-a)X(1)(k-1)

其中a属于[0，1]，通常可取0.5

建立灰微分方程：X(0)(k)+az(1)(k)=b

最小二乘解为：β=(a，b)T=(XTX)-1XTX0(k)

预测模型为：X(0)(k)=X(1)(k)-X(1)(k-1)

2.2 运算结果

初始化建模原始序列：5905，6325.74，6155.91，6283，7157，7695，9369，10751，12146.95

原始序列的1-AGO生成：5905.0000，12230.7400，18386.6500，24669.6500，31826.6500，39521.6500，48890.6500，59641.6500，71788.6000

1-AGO生成序列的紧邻均值生成：9067.8700，15308.6950，21528.1500，28248.1500，35674.1500，44206.1500，54266.1500，65715.1250

计算灰色模型发展系数a和灰色作用量b：a=-0.113，b=4370.139

模拟值与模拟误差见表9。

表9 模拟值与模拟误差

计算平均模拟相对误差：5.521%。

预测合肥市2021～2023年的房价(元/m2)：13150.623，14721.647，16480.351。

3 结论与建议

城市化率、居民消费价格指数、第三产业房地产业、房地产开发投资额影响因素指标对合肥市房价影响程度较大，合肥市2021～2023年的平均房价为13150.623元/m2，14721.647元/m2，16480.351元/m2。

基于上述结论，考虑合肥市可持续化健康发展的市场经济，提出以下建议：各级政府实施宏观政策管控，保证城市化率、居民消费价格指数、第三产业房地产业、房地产开发投资额等影响因素平稳发展。扩大合肥城市圈，将政策资源合理倾斜给四县一市，在确保交通、教育、经济的条件下，城市圈范围的扩大不仅能让房地产行业更加景气，更能带动长三角城市群的进一步发展。