广州市青少年业余举重运动员形态模型研究

胡雪银

前言

专项训练打造专项形态，不同的运动项目具有不同的专项形态特征。专项形态的研究多停留在优秀运动员的高度，对于竞技体育后备人才专项形态的研究较少。青少年运动员较优秀运动员有其自身的身体形态结构特点，故对竞技体育后备人才身体形态的研究是必要的。本文将从以下三个方面构建广州市青少年举重员的形态模型：形态指标模型、形态权重模型及形态均值模型，以填补以往研究对竞技体育后备人才形态研究的空白，为广州市竞技体育后备人才的科学选材提供参考依据。

1 研究对象与方法

1.1 研究对象

本文以234名广州市各区业余体校举重运动员的身体形态为研究对象。

1.2 研究方法

1.2.1 文献资料法

依研究需要，查阅相关文献及书籍，了解有关举重项目竞技体育后备身体形态特征的研究现状。

1.2.2 实验研究法

依据专家访谈的结果对广州市各业余体校的234名举重运动员的身体形态指标进行实地测量。

1.2.3 数理统计法

本研究应用SPSS21.0统计软件对举重运动员身体形态指标进行统计学分析，并采用因子分析对青少年举重运动员形态特征进行描述，同时赋予各形态指标不同的权重，挑选出最能反映出青少年举重运动员专项形态特征的指标。

2 研究结果与分析

2.1 广州市青少年业余举重运动员形态指标模型

为优化选材指标和简化选材过程，本文主要通过以下步骤完成对青少年举重运动员形态指标的筛选。首先，梳理与举重运动员专项形态模型、青少年生长发育特点相关的文献及书籍，挑选出能反映出青少年举重运动员形态特征的指标；其次，征求相关领域专家意见，剔除与举重运动员形态特征相关性较小的指标；最后，引入复合指标，通过逻辑分析剔除反映专项形态特征相关较大的指标，以保持指标之间的独立性，避免指标在反映专项形态特征上的重复性。最终初选指标：身高、髂宽、克托莱指数、上臂紧围、髂宽指数、胸围、体型指数、脚掌长等8个指标。

2.2 广东省业余体校举重运动员形态指标权重模型

本文旨在构建广州市业余体校举重运动员的形态模型，在确立形态指标模型的基础上，利用因子分析法确定指标的权重。以形态指标模型为基本变量进行因子分析，找出各指标与专项形态的共性关系。首先对主成分分析法的结果解释总方差进行分析（见表1）。

表1 解释的总方差

通过表2观察各形态因子的初始特征值与方差百分比，可得出此次因子分子主要提取了两个主成分因子。且因子1和因子2的累进方差贡献率达到85.732%，说明这两个因子包含整体85.732%的信息，即可认为其他变量对整体的影响可以忽略不计，因此可以用这两个主成分来反映举重运动员的专项形态特征。同时，因主成分1和主成分2的初始特征值和方差百分比不同，所以这2个主成分在反映形态特征上的权重也应有所差别。根据因子1、因子2的方差百分比结合这两个主成分的累进贡献率可得出主成分因子1的权重为0.66%，因子2的权重为0.34%。由此可知，因子1较因子2更能反映青少年举重运动员专项身体形态。

表2 旋转成分矩阵

形态指标的因子载荷反映其与两个主成分因子的相关度，据表2可知，胸围、上臂紧张围、身高、脚掌长和克托莱指数、髂宽在因子1中所在比重较大，表明因子1主要由以上6各指标构成。在这6个指标中，克托莱指数主要反映单位身高上的体重常用来描述运动员的肌肉质量；髂宽和胸围、上臂紧张围分别是反映人体横向、纵向发育程度的重要指标［7］［8］，髂宽和胸围上臂紧张围越宽表明肌肉附着越多，以上指标都可反映出举重运动员专项形态结构上的肌肉质量，因此我们将因子1界定为肌肉质量因子；同理，髂宽指数和体型指数在因子2中所占权重较大，最能反映因子2的特征，又因以上指标均为反映人体身体形态的重要指标，所以我们将因子2定名为体型因子。

根据各形态因子载荷可计算各形态指标的权重（见表3），由表4可知，胸围、克托莱指数、上臂紧张围在因子1中占有较大权重，其次为身高、脚掌长；因子2中体型指数和髂宽指数占有较大权重，以上各形态指标在因子中权重的分布状况可以证明本文对两个主成分因子定名是正确的。另外，各指标在反映专项形态的最终权重中，以髂宽、髂宽指数占有最大权重，说明这两个指标最能反映广州市青少年举重运动员的专项形态特征。

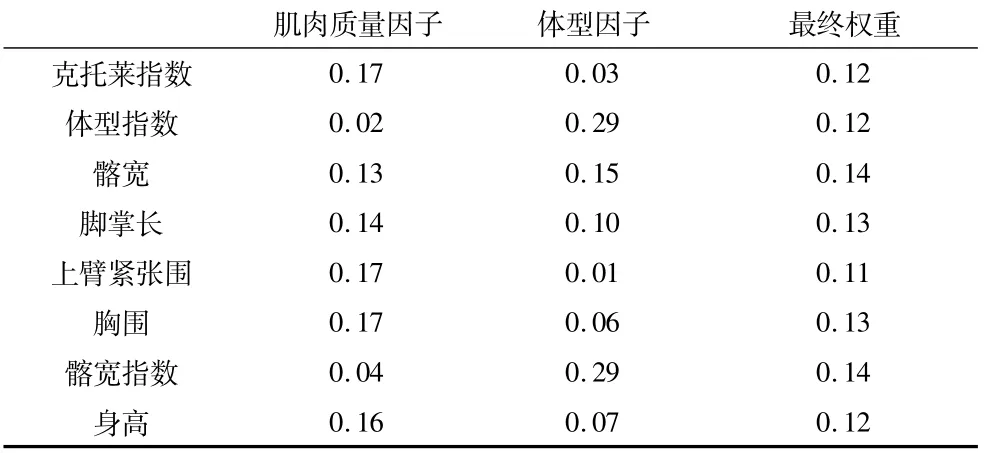
表3 各因子中各指标权重

表4 广州市业余体校举重运动员形态各指标的均值标准差（m±s）模型

明确形态指标在反映专项形态上的最终权重是构建形态指标权重模型的关键，因子内各指标所占的权重只能反映其所在因子的重要性程度，不能反映其对专项形态的重要程度。由上述可知，各主成分因子在反映专项形态的信息量上不同，而各形态指标在两个主成分因子上权重各异［9－10］。形态指标的最终权重可根据主成分因子所占的权重与形态指标在两个主成分因子中所占权重得出（计算公式为：最终权重＝0.66×因子1中权重＋0.34×因子2中权重）。

2.3 广东省业余体校举重运动员形态指标的均值模型

在各形态指标中，体重是区分举重竞赛等级的重要标准。因此本文在构建广州市青少年举重运动员形态模型的时剔除了体重这一指标，使所构建的权重模型能适用于不同竞赛等级的举重运动员，但构建形态均值模型，则必须以体重为分类变量，构建不同重量级举重运动员的形态均值模型，其目的在于了解不同竞赛等级举重运动员在专项形态上的差异。

本文以世界青少年举重联合会的参赛等级划分为依据，结相关专家及教练员的访谈意见，依体重的不同划分为3个竞赛等级：男94kg以上级、94 kg级，85级，女69 kg以上级、69kg级、63kg级；中量级：男69 kg级、77 kg级、62 kg级，女53 kg级、58kg级；轻量级：男50 kg级、56 kg级，女44kg级、48 kg级。由表5可知，不同竞赛等级的业余举重运动员的形态均值模型不同，从而可以认为分重量级构建广州市青少年举重运动员形态均值模型的想法是正确的。应用单因素分析发现不同重量级的运动员形态均值模型的具有显著性差异，表现为重量级大于中量级大于轻量级，以肌肉质量因子中胸围、身高、髂宽较为显著，且其差异具有显著性；但髂宽指数在重量级、中量级、轻量级之间的差异较小。综上所述，广州市业余体校举重运动员不同竞赛等级间，专项形态差异主要表现在肌肉质量因子上。造成这种差异的原因主要是因为不同重量级别是依据体重的不同来划分的，较高的体重，将必然在髂宽、胸围、克托莱上占据一定的优势；但体重的差异对体型因子影响较小。

表5 不同竞赛等级各因子与因子总分的标准分（m±s）比

3 广东省业余体校举重运动员不同重量级专项形态差异

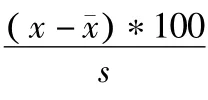
通过计算肌肉质量、体型、形态总分来减少分析的维度，已达到在全面反映不同竞赛等级运动员专项形态特征的基础上简化分析过程。在指标数值标准化的前提下，根据各形态指标在各主成分因子中所占权重，计算肌肉质量因子、形态总分和体型因子。公式如下：

肌肉质量因子＝0.17x1＋0.02x2＋0.13x3＋0.14x4＋0.17 x5＋0.17x6＋0.04x7＋0.16x8

体型因子＝0.03x1＋0.29x2＋0.15x3＋0.10x4＋0.01x5＋0.06x6＋0.29x7＋0.07x8

形态总分＝0.66×肌肉质量因子＋0.34×体型因子

其中，x1代表克托莱指数，x2代表体型指数、x3代表髂宽、x4代表脚掌长、x5表示上臂紧张围、x6表示胸围、x7表示髂宽指数、x8表示身高。根据以上公式，计算出肌肉质量因子、体型因子、形态总分的平均数和标准差，对比不同竞赛等级的平均数和标准差。可得轻量级举重运动员的专项形态得分与轻量级之间差距明显大于轻量级与重量级；不同重量级别之间的体型得分的差异小于肌肉质量得分，并呈现出重量级优于中量级优于轻量级；综上所述，随着重量级别的提高，形态总分、肌肉质量和形态因子的得分逐步提高，上述结论表明伴随竞赛等级的上升专项形态也随之表现出适于举起更高重量的专项形态。

4 结论

4.1 采用因子分析主成分分析法，将广州市业余体校青少年举重运动员形态分为两个因子，即肌肉质量因子和体型因子，肌肉质量因子的所占的权重大于体型因子，肌肉质量因子的权重为0.66，体型因子的权重为0.34。

4.2 不同重量级别的举重运动员在专项形态上的得分差异具有显著性，并呈现出重量级得出大于中量级大于轻量级。表明广州市业余体校举重运动员随着重量级别的提高，表现出更适于举起更高重量的专项形态特征。

4.3 建立了广州市业余体校青少年举重运动员身体形态模型，为广州市青少年举重运动员的选材和训练提供参考依据。