考虑含钢率影响的核心型钢-混凝土组合柱受压计算分析
张 科
(衡阳公路桥梁建设有限公司,湖南 衡阳 421000)
随着我国经济建设大力发展,修建的结构物不断朝着高层、超高层发展,而传统的钢筋混凝土柱延性差、混凝土易开裂、易压碎破坏,限制了高层与超高层建筑的发展,同时也不利于结构抗震[1-2]。对此,郭子雄等[3]提出了核心型钢-混凝土组合构件,即在混凝土柱内埋置型钢结构并配置一定的钢筋量,形成一种新型的组合结构;该结构不仅能同时发挥钢筋混凝土和型钢结构的特点,而且截面尺寸小、承载力高,同时型钢外包混凝土可有效防止型钢在复杂环境下的锈蚀,解决防火问题,避免了钢材局部屈曲,弥补了传统钢筋混凝土柱结构延性不足的缺陷,可大大提高结构的抗震能力[4-5]。
目前,对于型钢-混凝土柱结构的研究越来越多,成为近年来研究的热点问题之一。惠存等[6]以实际工程中矩形截面的型钢-混凝土柱为背景,开展了轴心和偏心荷载下的单调加载试验研究,发现型钢-混凝土柱结构具有很好的塑性变形能力和延性。Ellobody等[7-8]也开展了型钢-混凝土组合柱在轴心、偏心和温度荷载下的力学性能研究,发现混凝土柱内嵌型钢可有效提高组合柱的受力性能。Tokgoz等[9-10]开展了核心型钢-L型钢纤维高强钢筋混凝土组合柱的双向偏心受压试验研究,以研究组合柱的受压性能。贾磊鹏等[11]开展了核心型钢-混凝土组合柱的轴心受压试验和ABAQUS有限元分析,研究其轴心受压性能和设计方法。刘阳等[12]进行了核心型钢-混凝土组合柱的抗震性能和轴压比限值试验的低周往复拟静力试验研究,提出了组合柱轴压比限值的建议取值。周乐等[13-14]开展了核心型钢-混凝土组合柱的轴压试验,研究其在负载下加固后的力学性能和破坏模式。李奉阁等[15]开展了2榀型钢混凝土柱-钢梁框架的低周往复拟静力试验研究,分析了其滞回性能、耗能能力等。马辉等[16]开展了9根圆形钢管型钢-再生混凝土组合短柱的轴心受压试验,分析了径厚比和含钢率对其轴压性能的影响。含钢率为影响核心型钢-混凝土组合柱受压性能的重要参数,然而,当前对于在不同含钢率影响下组合柱的破坏特征和极限承载力的计算研究还不多,仍有待进一步深入分析。
为此,本文在前人研究的基础上,采用ABAQUS数值分析与理论计算相结合的方法对核心型钢-混凝土组合柱在轴向荷载下的受压破坏特征与极限承载力计算展开研究,在现有钢筋混凝土轴心受压构件计算理论的基础上考虑含钢率的影响,并对不同含钢率下组合柱的极限受力行为进行了深入分析,为组合柱的设计计算与相关工程应用提供参考。
1 核心型钢-混凝土组合柱的设计与有限元建模
为了进一步确定核心型钢-混凝土柱设计的合理性,本文在文献[15]的基础上对其受压力学性能计算分析,文献[15]采用的是钢骨混凝土柱-钢梁框架结构,本文仅取其钢骨混凝土柱作为计算模型,并与文献[15]采用相同的核心型钢-混凝土柱截面尺寸以及混凝土、型钢和钢筋的基本力学参数。
含钢率研究参数分别为0%、2.83%、3.54%、4.25%、5.66%和7.08%,分别命名为S-RC-0~S-RC-5。核心型钢-混凝土柱高H为1.2 m,采用尺寸200 mm的正方形截面,混凝土柱内配置了4Φ12纵向钢筋和Φ6@100箍筋,钢筋保护层厚度为15 mm。
采用ABAQUS通用有限元软件进行核心型钢-混凝土柱的建模分析,假定混凝土与型钢浇筑牢固,采用面面绑定(Tie),纵向钢筋与箍筋合并成一个钢筋笼嵌入(Embedded region)混凝土柱内,同时于柱底面设置一块截面尺寸为b×h×t=600 mm×500 mm×100 mm的混凝土垫块,核心型钢-混凝土柱底面与混凝土垫块顶面进行Tie约束,混凝土垫块底面采用固结。
分析中,采用分步位移轴向加载,设定最终加载位移为10 mm,加载增量2 mm。在柱顶10 mm位置处设置参考点RP,参考点与柱顶面采用耦合(Coupling),位移施加在参考点之上。有限元模型见图1。

图1 有限元模型及其边界约束
2 核心型钢-混凝土组合柱受压性能计算分析
2.1 外包混凝土柱的破坏行为
图2给出了受不同含钢率影响的外包混凝土柱受压破坏情况,图3给出了外包混凝土柱最严重破坏位置与含钢率关系,其中,最严重破坏高度是指破坏位置至柱顶的距离。
由图2可知,组合柱的含钢率增大,外包混凝土的塑性应变随之减小,混凝土压碎破坏有所改善,同时混凝土破坏的范围更宽,减小了应力集中,可有效改善混凝土柱的局部破坏。此外,由图3可以发现,外包混凝土柱的破坏位置与含钢率表现为非线性关系,关系曲线存在2个不同阶段,分别为无含钢率和受含钢率影响阶段。当含钢率逐渐减小至0时,外包混凝土柱的破坏位置会逐渐朝着柱底部发展,不利于结构整体受力,这是引起整体结构垮塌的主要原因。而当含钢率逐渐增大时,引起组合柱的内力重分布,外包混凝柱的破坏位置逐渐朝柱中部发展,受力更为均匀。

a)S-RC-1
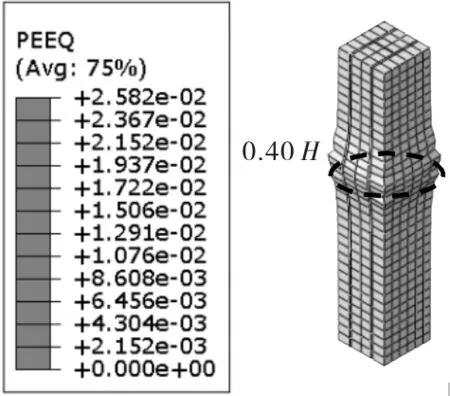
b)S-RC-2

c)S-RC-3

d)S-RC-4
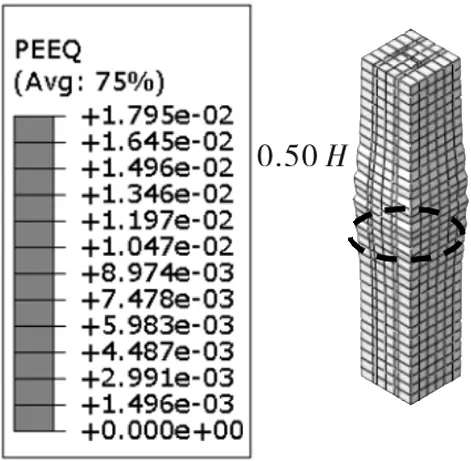
e)S-RC-5
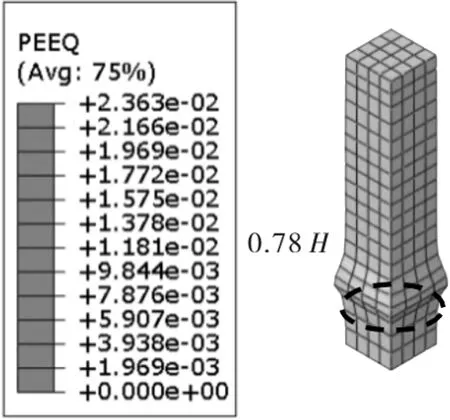
f)S-RC-0
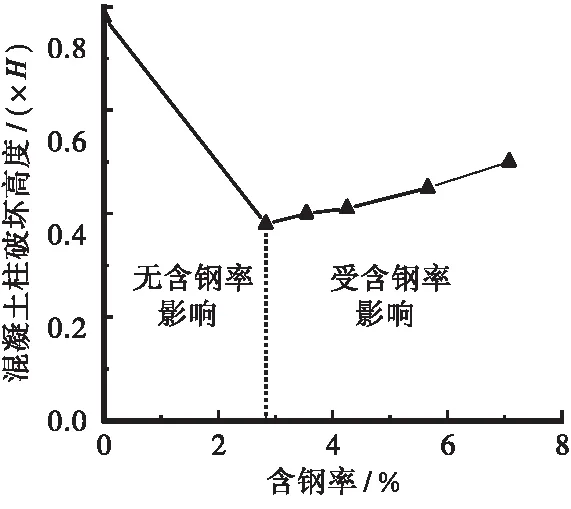
图3 外包混凝土柱最严重破坏位置-含钢率的关系曲线
2.2 内嵌型钢柱的破坏行为
图4给出了受不同含钢率影响的内嵌型钢柱受压破坏情况,图5给出了内嵌型钢柱最严重破坏位置与含钢率关系,其中不包括S-RC-0组合柱,因其含钢率为0,即无内嵌型钢柱,图中给出的最严重破坏高度是指破坏位置至柱顶的距离。
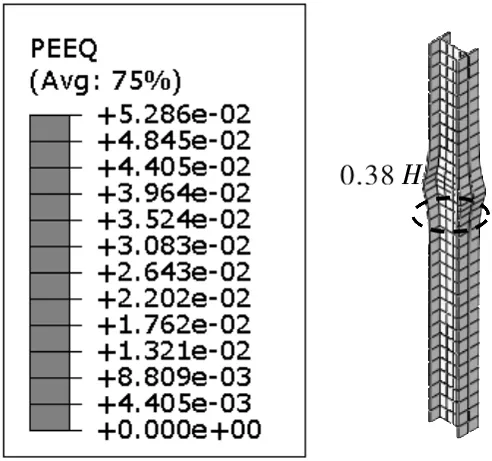
a)S-RC-1

b)S-RC-2
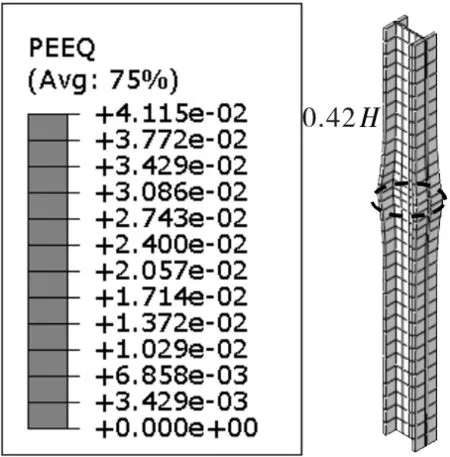
c)S-RC-3
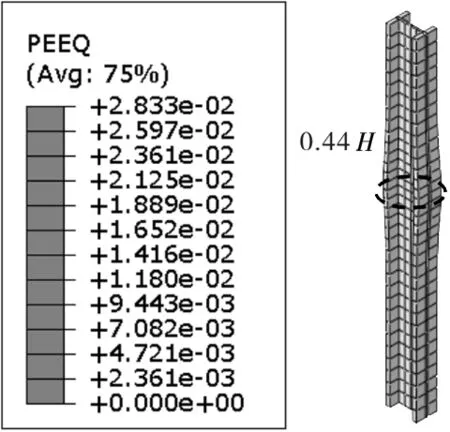
d)S-RC-4
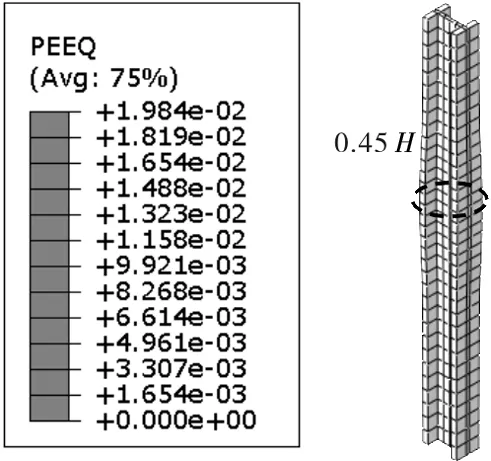
e)S-RC-5
由图4可知,组合柱设计的含钢率越大,内嵌型钢的塑性应变越小,外包混凝土有效地保护了型钢的受力,可延缓型钢柱过早屈服,同时破坏的范围也更宽,可有效避免型钢的局部屈曲现象。由图5可知,内嵌型钢柱的破坏位置与含钢率表现为近似线性关系,随着含钢率增大,内嵌型钢柱的最严重破坏位置沿着柱中部发展,与外包混凝土柱破坏的发展规律相似。

图5 内嵌型钢柱最严重破坏位置-含钢率的关系曲线
2.3 组合柱受压极限承载力计算
对组合柱极限承载力的极限进行分析,此处采用承载力占比ξsc来定义内嵌型钢柱在组合柱中承受外部荷载的贡献,可通过式(1)进行计算:
(1)
式中:Fsc为组合柱的极限承载力,kN;Fc为外包混凝土柱的极限承载力,kN。
通过式(2)可计算出不同含钢率下型钢柱承载比变化情况,详见图6。由图6可以看出型钢柱承载比随着含钢率增大而提高。通过线性拟合方法,可得到型钢柱承载比与含钢率成正相关,如图6所示,变异系数R2=0.999 4,说明了拟合曲线能很好地体现两者变化情况。
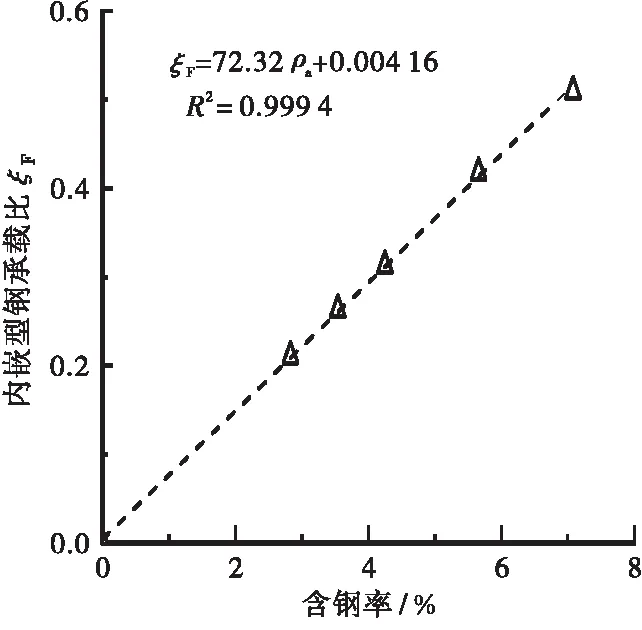
图6 型钢承载比-含钢率曲线
ξF=72.32ρa+0.004 16
(2)
我国现行《混凝土结构设计规范》(GB50010—2010)[17]和《型钢混凝土组合结构技术规程》(JGJ 138—2001)[18]分别规定了钢筋混凝土轴心抗压柱和型钢-混凝土轴心抗压柱的极限承载力计算,详见式(3)~式(5)。
Nc=0.9φfcAc+fyAy
(3)
Nsc=φfcAc+fyAy+fsAs
(4)
Nsc=1+ξsc·0.9φfcAc+fyAy
(5)
式中:Nc为钢筋混凝土柱轴向压力设计值,N;Nsc为型钢-混凝土组合柱的轴向压力设计值,N;φ为钢筋混凝土柱的稳定系数;fc为混凝土轴心抗压设计值,MPa;A为构件截面面积,mm2;fy为钢筋抗压强度设计值,MPa;Ay为全部纵向钢筋截面面积,mm2;fs为型钢抗压强度设计值,MPa;As为型钢截面面积,mm2;
采用式(3)可计算得到钢筋混凝土轴心抗压柱的极限承载力值,通过考虑型钢柱承载力占比ξsc系数的影响,即可计算得到不同含钢率下组合柱的极限承载力,如图7所示。由图7可知,采用式(4)和式(5)可较为准确地计算型钢-混凝土组合柱的极限承载力,相比式(5)的计算精度较好,进一步验证了数值计算模型的合理性。
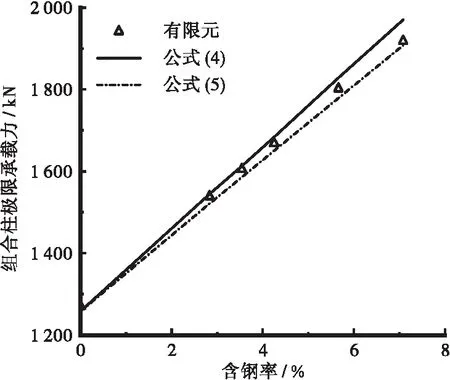
图7 型钢-混凝土组合柱的极限承载力计算值
3 结论
以核心型钢-混凝土组合柱为研究对象,基于有限元与理论分析相结合的方法,通过ABAQUS软件建立了组合柱的三维实体有限元模型,研究了不同含钢率对外包混凝土柱和内嵌型钢柱的破坏特征以及对组合柱极限承载力的影响,结论如下:
1)组合柱的含钢率增大,外包混凝土的塑性应变随之减小,混凝土压碎破坏有所改善,同时混凝土的破坏范围更宽,减小了应力集中,可有效改善混凝土柱的局部破坏。
2)组合柱设计的含钢率越大,内嵌型钢的塑性应变越小,外包混凝土可有效保护型钢的受力,延缓型钢柱过早屈服,同时破坏的范围也更宽,能有效避免型钢的局部屈曲现象。
3)外包混凝土柱的破坏位置与含钢率表现为非线性关系,内嵌型钢柱的破坏位置与含钢率表现为近似线性关系。而型钢承载比随着含钢率增大而提高,两者成正相关。
4)考虑型钢承载比的钢筋混凝土柱极限承载力理论公式,可更为准确地计算组合柱的极限承载力,且较好地与有限元计算结果吻合,验证了有限元模型的合理性。

