漏斗形岩溶洞穴土质盖层稳定性分析方法

朱学坤， 王小委， 李洪梅

(江西交通职业技术学院 路桥工程系， 江西 南昌 330013)

0 引言

岩溶塌陷是指可溶岩洞隙上方的岩、土体在自然或者人为因素作用下产生变形破坏，并在地面形成塌陷坑(洞)的一种岩溶动力地质作用与现象，其实质是在地壳运动和演化过程中由内、外地质营力相互制约、相互作用及影响，使得致塌力超过抗塌力而产生的结果，是岩溶地区广泛存在的地质灾害之一[1]。据统计，我国目前有详细记录的岩溶塌陷1500多起，形成的塌陷坑数量45000多个，由岩溶塌陷带来的经济损失巨大[2]。

关于岩溶塌陷形成机理，国内外研究成果较多，概括起来主要包括真空吸蚀理论、渗透潜蚀理论和气爆理论等[3-5]，而针对岩溶塌陷发生前盖层的稳定性问题，相关文献报道较少。岩溶塌陷是多因素耦合作用的结果，且塌陷形成过程漫长，为更好地揭示岩溶地区塌陷发生机理，及时预报塌陷灾害，必须对岩溶洞穴盖层稳定性进行分析。彭祖武等[6]引用基础工程学中矩形独立承台受柱冲切计算模型，推导了岩溶地面塌陷阶段计算公式，公式能很好地预测湘中地区典型岩溶塌陷，但该方法只适用于盖层为坚硬岩体的情况，对于松散土质盖层适用性欠佳；贺可强等[7]基于极限平衡理论建立了考虑渗压效应的塌陷模型，并对枣庄市岩溶塌陷进行了分析验证，表明建立的塌陷模型一定程度上能预测盖层稳定性，但该模型忽视了洞穴盖层局部稳定性问题；陈洪凯等[8]运用ANSYS软件得到了地表拉压应力区范围拟合公式，提出了直桶形岩溶塌陷洞穴盖层稳定性计算公式，但用软件拟合得到的公式适用性并未得到论证，且研究直桶形岩溶塌陷洞穴盖层稳定性问题缺乏代表性。

本文基于普氏理论和极限平衡理论，在现有计算方法的基础上，研究漏斗型岩溶洞穴土质盖层稳定性分析方法，以期进一步完善岩溶洞穴盖层稳定性计算方法，为科学预测岩溶塌陷灾害提供理论支撑。

1 漏斗形岩溶塌陷实物模型

岩溶塌陷发生时从外观上看主要呈现漏斗形、直桶形和坛形3种破坏形态[9]，而其中漏洞形占多数，图1a为典型漏斗形岩溶塌陷。根据图1a，构建漏斗形岩溶塌陷实物模型，如图1b。

漏斗形岩溶塌陷的发生往往是由于地下水快速下降产生真空负压所致，破坏过程呈现连续性。针对漏斗形岩溶塌陷破坏模式主要有2种观点: ①认为岩溶洞穴上部盖层首先发生的是直桶形破坏，之后洞穴两侧土体因为失去支撑，发生沿破裂角的剪切破坏，即外观上呈现漏斗形；②认为岩溶洞穴上部盖层首先发生的是坛形破坏，之后因为局部坍塌破坏，形成漏斗形。

a) 漏斗形岩溶塌陷现场

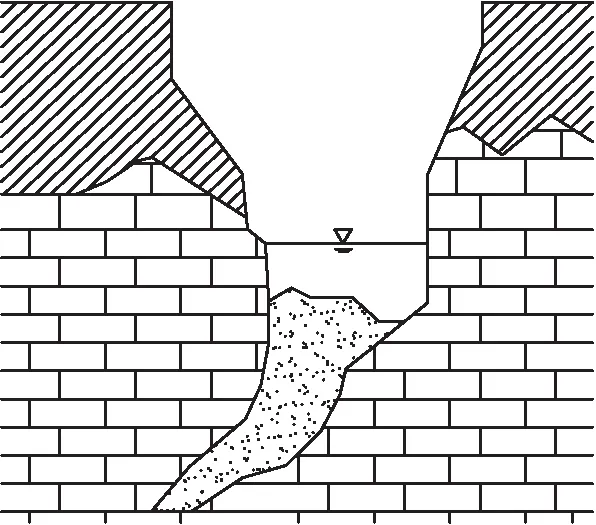
b)漏斗形岩溶塌陷实物模型

本文不深究漏斗形岩溶塌陷发生的本质，着眼于塌陷发生后的结果，将盖层塌陷体视为整体，分析盖层稳定性。

2 漏斗形岩溶塌陷土质盖层稳定性计算

根据图1漏斗形岩溶塌陷现场图，构建漏斗形岩溶塌陷土质盖层稳定性计算简化模型(见图2)。鉴于漏斗形岩溶塌陷发生的本质本文未作深究，以如下基本假定，方便下文漏斗形岩溶塌陷土质盖层稳定性计算公式的推导。

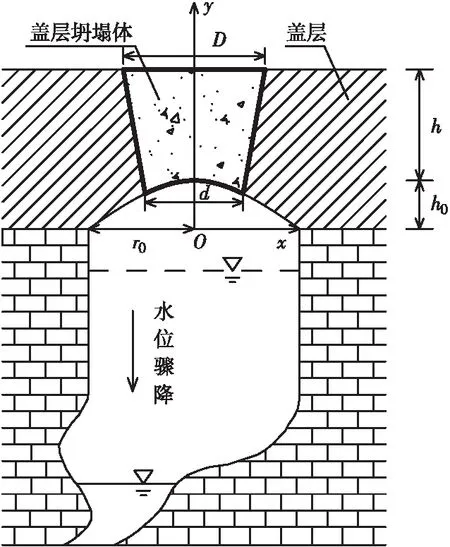
图2 漏斗形岩溶塌陷土质盖层稳定性计算简化模型

2.1 基本假定

1) 地下水位于盖层以下；

2) 坍塌体呈漏斗形，断面呈梯形，沿两侧斜面发生剪切破坏；

3) 盖层土体为一整体均质结构，且不考虑由于降雨渗入产生的渗透力和导致的盖层土体强度弱化；

4) 盖层底部非平面，而是呈现满足普氏平衡拱理论的二次抛物面。

按照普氏理论，平衡拱轴线方程如式(1)：

(1)

式中：y为对应水平距离为x处坍落拱高度，m；x为水平距离，m；r0为坍落拱半跨距离，m；fk为坚固性系数；λ为拱高度修正系数，通常情况下取λ=0.828；h0为拱顶高度，m。

2.2 盖层坍塌体受荷分析

将盖层坍塌体视为一整体，从周围隔离出来进行力学分析，如图3所示。

图3 盖层坍塌体力学分析

2.2.1盖层坍塌体自重G计算

在不考虑降雨情况下，盖层坍塌体自重G可按式(2)计算。

G=Gyt-Ggd

(2)

式中：Gyt为圆台型盖层坍塌体自重,kN；Ggd为圆台型盖层下部缺失体重,kN。

圆台型盖层坍塌体自重Gyt和圆台型盖层下部缺失体重Ggd可按式(3)、(5)计算。

(3)

(4)

Ggd=γVgd

(5)

(6)

式中：γ为盖层土体的天然容重，kN/m3；hs为圆台型盖层坍塌体高度，m；D、d分别为圆台型盖层坍塌体顶、底面宽度，m；h为圆台型盖层坍塌体顶面到坍塌拱顶距离，m；Vgd为圆台型盖层下部缺失体体积，m3。

将式(3)～(6)代入式(2)，整理得到盖层坍塌体自重G如式(7)：

(7)

2.2.2盖层坍塌体侧摩阻力Ff计算

盖层坍塌体两侧斜面任意一点土的抗剪强度满足库伦抗剪强度公式，如式(8)所示。

τf(z)=σ(z)tanφ+c

(8)

式中：τf(z)为盖层坍塌体两侧斜面任意一点土的抗剪强度，kPa；σ(z)为盖层坍塌体两侧斜面任意一点土所受到的法向应力，kPa；c为盖层坍塌土体粘聚力,kPa;φ为内摩擦角，°。

假定盖层坍塌土体在竖直方向和水平方向分别受到大主应力和小主应力作用，按一点的应力状态理论，盖层坍塌体两侧斜面任意一点土所受到的法向应力σ(z)计算公式如(9)。

σ(z)=k0γzsin2α+γzcos2α

(9)

(10)

式中：k0为侧压力系数(可查表)；z为深度，m；α为两侧斜面倾角，°。

盖层坍塌体侧摩阻力Ff按式(11)计算。

(11)

2.2.3盖层坍塌体所受到的真空负压力P计算

鉴于盖层坍塌体顶部大气压强p1和底部大气压强p2监测数据较难获取，本文笼统以真空负压Δp计算真空负压力P，如式(12)。

(12)

式中：P为盖层坍塌体所受到的真空负压力，kN；Δp为由地下水骤降产生的真空负压，kPa，文献[7]建议根据经验在0～100 kPa之内取值。

2.3 盖层坍塌体稳定性计算及判定

根据前述盖层坍塌体受荷分析，定义盖层坍塌体稳定性系数K：

(13)

若K<1，盖层坍塌体处于非稳定状态；若K=1，盖层坍塌体处于极限平衡状态；若K>1，盖层坍塌体处于稳定状态。

3 工程实例

莲花县位于江西省西部，萍乡市南部，东北与安福县接壤，东南与永新县毗邻，西南与湖南省茶陵县、攸县相连，北面与芦溪县交界。县内地貌由山地、丘陵、岗地、河谷平原和山间盆地组成，地势北、东、西3面高，中部和南部低。截止到2017年，莲花县城区累计发生地质灾害27起，其中岩溶塌陷灾害达19起，占已发送地质灾害总数的70%。平均每1 km2就有一处塌陷，且以中、小型居多，平面呈圆形，直径一般为1～6 m，深度为1～10 m不等。多年来，莲花县因为岩溶地面塌陷灾害导致直接经济损失达120万元[10]。在全国基础设施建设步伐加快的背景下，莲花县城区岩溶地面塌陷灾害有加剧趋势。

根据对莲花县城区岩溶塌陷坑的现场调查，发现某处塌陷点(命名为D1)比较典型，符合本文研究对象所具有的漏斗形塌陷特征，如图4。D1塌陷点洞穴顶部盖层土体为粉质粘土，土体天然容重为19.5 kN/m3，室内直接剪切试验揭示该土体内摩擦角φ=23°，粘聚力c=18 kPa。D1塌陷点盖层坍塌体顶部宽度D=5.2 m，底部宽度d=2.4 m，高度h=6.1 m，坍落拱半跨距离r0=3.0 m。查阅《工程地质手册》，普氏坚固性系数fk=0.6，静止土压力系数k0=0.45。将以上数据代入公式(7)、(11)和(12)，并最终代入公式(13)中得：

图4 莲花县城区D1塌陷点

(14)

将上述公式在MatLab中绘出，如图5所示。分析图5可知，漏斗形岩溶洞穴土质盖层稳定性随真空负压的升高而降低，鉴于D1岩溶塌陷点已经发生，即稳定性系数K<1，可推测岩溶塌陷发生时，由地下水位下降导致的真空负压达93 kPa以上，与实际吻合较好。

4 结语

岩溶塌陷是灰岩地区广泛存在的地质灾害之一，灾害发生时往往在地表形成塌陷坑，给人民出行、安全带来不良影响，造成的经济损失巨大。本文以漏斗形岩溶塌陷为研究对象，深入分析了漏斗形岩溶洞穴土质盖层稳定性，主要结论如下：

1)基于极限平衡和普氏平衡拱理论，定义了漏斗形岩溶洞穴土质盖层稳定性，构建了相应稳定性计算公式，并提出了稳定性判据。

2)以莲花县城区典型岩溶塌陷点D1为实例，得到了D1塌陷点在未发生塌陷前盖层稳定性系数与真空负压的关系式，并得到了相应关系曲线，反推出D1塌陷点发生坍塌时，由地下水位下降产生的真空负压可达93 kPa以上，与实际吻合较好。

可见，本文提出的漏斗形岩溶洞穴土质盖层稳定计算公式具有一定的理论参考价值。但本文在分析过程中未考虑降雨入渗导致的渗流和土质盖层强度参数的弱化方面的影响，后续可从这两方面做进一步研究工作，以期得到更为精确的结论。