基于强化学习的多发导弹协同攻击智能制导律
陈中原, 韦文书, 陈万春
(1.北京航空航天大学 宇航学院, 北京 100191; 2.中国运载火箭技术研究院, 北京 100076)
0 引言
近年来,为提升打击效能,协同制导技术得到越来越多的关注[1-5]。协同制导的多发导弹可以看作是仅基于简单控制律即可相互协作以实现任务目标的多智能体系统[6]。多发导弹协同作战在效能上要优于单个高技术和高成本的飞行器。此外,多发导弹构成的多智能体系统也会比单个飞行器具有更强的作战能力[7]。其中,多发处于不同初始条件的导弹实现对目标的同时打击是一个极具挑战的问题[8-9]。
目前,多弹同时攻击协同制导律可以分为两类:
1) 第1类是为协同制导系统指定期望的攻击时间。Cho等[10]提出了一种非奇异滑模制导律使导弹在指定的时间打击目标;Liu等[11]基于自适应滑模设计了一种指定攻击时间和攻击角度的制导律。然而,为处于不同初始条件下的多发导弹指定同一个攻击时间显然是有困难的。此外,各发导弹间没有交互,降低了多弹协同制导系统对环境的感知能力。
2) 另一类是由系统中的各发导弹相互协调,对齐攻击时间。Jeon等[7]对比例导引制导律(简称PN制导律)进行拓展,设计了多弹协同攻击制导律。然而,该制导律要求每发导弹都要有整个系统的全局信息,为集中式控制,通讯负担较重。此后,Zhou等[12]基于李雅普诺夫理论设计了有限时间收敛的分布式协同攻击制导律。Sinha等[13]设计了一种超螺旋滑模制导律,使制导指令更加平滑。李文等[14]基于一致性理论,选取飞行器与目标的相对距离和接近速度为协调变量,设计了无动力飞行器在速度时变情况下的分布式时间协同三维制导方法。

在导弹制导方面,Cottrell等[17]设计了神经网络最优拦截制导律,减小了燃料消耗,有利于实现拦截器的小型化。然而,基于神经网络或深度学习网络[18]的制导律需要最优化样本进行训练,样本数量一定程度上决定了智能制导律可应用的交战环境,即某些不在样本中的交战环境可能使制导律失效。
为了简化制导律设计,提高制导律鲁棒性,Gaudet等[19]基于元强化学习设计了拦截器末制导律。南英等[20]对传统深度Q网络(DQN)的记忆池生成方法进行改进,提出了一种基于Markov决策过程的弹道导弹中段突防控制模型。强化学习技术不需要深度学习所需要的样本,也无需设计控制器的结构,可自主探索实现奖励值最大的动作。然而,上述智能制导律仅针对单个弹,而不是“弹群”。胡仕友等[21]总结了导弹武器智能精确制导技术的发展现状并对发展趋势做了分析,指出开展多弹间信息交互与协同处理技术研究,实现群体的分布式智能化协作,是未来导弹武器智能精确制导技术发展的重要方向。
基于深度确定性策略梯度(DDPG)的强化学习算法,引入Actor和Critic神经网络用于动作的选取和奖励值的逼近,用于解决复杂连续的控制问题[22-23]。本文基于DDPG设计了多弹同时攻击协同制导律。为了降低协同制导系统的通讯负担,利用多智能体思想,使协同制导系统中的每发导弹只需与自己的邻居进行通讯,实现了分布式协同制导。此外,本文方法不再假设初始航向角误差为小角度[7,10],因而具有更广的应用范围。
1 问题描述
1.1 平面交战几何模型
考虑如图1所示的n发导弹和一个静止目标间的平面交战几何关系,图1中:vmi为第i发导弹的速度;θi为弹道倾角;ri为第i为导弹和目标的相对距离;λi为弹目视线角;σi为第i发导弹的航向角误差;ami为导弹指令加速度。系统的非线性交战动力学方程为
图1 多弹协同制导平面交战几何关系Fig.1 Planar engagement geometry
(1)
需要说明的是,这里假设各发导弹的速度大小为常值,导弹加速度的方向垂直于导弹速度。
由于本文所研究的是气动控制的导弹,也就是只有速度方向可被气动力控制,而导弹的轴向速度是不可控的。因此,制导指令垂直于速度方向。另外,导弹末制导阶段飞行距离和制导时间较短,目标为静止目标,可忽略导弹速度大小变化,因此导弹速度假设为常值。
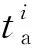
(2)

(3)
式中:Ni为比例导引常数。然而小角度假设不能够接近实际,因此本文中考虑初始航向角误差较大时,剩余飞行时间由(4)式估计,即
(4)
1.2 图论
随着协同制导系统中导弹数量的增加,图论成为描述导弹间信息交互关系的有力工具。考虑一个有n发导弹的协同制导系统,系统拓扑可以表达为Gs=(Vs,Es,As),其中:Vs={1,2,…,n}为拓扑图形中顶点的集合,代表每发导弹的位置;Es⊆Vs×Vs拓扑图形中边的集合;As=[aij]是拓扑图形Gs的邻接矩阵[24]。顶点i和顶点j的边由(j,i)∈Es来表达,代表第i发导弹可以获取第j发导弹的信息。邻接矩阵As定义为:当且仅当(j,i)∈Es时,aij=1,如果(j,i)∉Es则aij=0.此外,邻居的集合定义为Ni={j∶(j,i)∈Es}.第i个顶点的自由度由di来表示,di为第i发导弹邻居的个数。拓扑图形Gs的自由度矩阵可以表达为Δ=diag{di},i∈[1,2,…,n].拓扑图形Gs的拉普拉斯矩阵La定义为
La=Δ-As,
(5)
La代表了多弹协同制导系统中导弹间的信息交互关系。
根据文献[25-27]:若多导弹协同制导拓扑的基础图是固定且无向的,当且仅当拓扑图连通时,多发导弹可实现到达时间的一致;若拓扑的基础图为有向图,当且仅当拓扑图含有一个生成树时,利用强化学习算法,多发导弹可实现到达时间的一致。
1.3 拟解决的问题
针对多导弹协同制导系统, 需设计一个分布式协同制导方案,使多发导弹在不同初始条件下实现同时打击目标。根据(2)式,若各发导弹的剩余飞行时间达到一致,那么多发导弹即可实现对目标的同时打击。定义剩余飞行时间估计的一致性误差为
(6)
即第i发导弹与其邻居间估计剩余飞行时间的误差。
因此,需要设计一个协同制导律来实现下面3个目标:
1) 所有导弹都要击中目标,即脱靶量为0 m;
2) 所有导弹剩余飞行时间估计的一致性误差要变为0 s,实现同时攻击;
3) 当剩余飞行时间估计的一致性误差为0 s时,各发导弹可利用简单的制导律继续飞行,当有剩余飞行时间误差时,继续进行调整。
由于传统方法在设计制导律时需要仔细调整制导律中的各个参数,来实现期望的性能。本文将尝试应用强化学习技术来设计制导律,无需关心制导律结构及参数设计,实现智能协同制导。
2 协同攻击制导律设计
2.1 协同制导律的结构
受文献[25]的启发,协同制导律的结构设计为
(7)

(8)
2.2 基于强化学习的协同制导律
如1.1节所述,剩余飞行时间的估计表达式为
(9)
其对时间的1阶导数为
(10)
那么多弹协同制导系统剩余飞行时间一致性误差对时间的导数可等效为如(11)式所示的非线性系统:

(11)


(12)
式中:q(x(t))为脱靶量和一致性误差的函数。
本文目标就是寻找一个状态反馈控制器u*=Φ(x),使得非线性系统式的性能指标式达到最小化。求解该问题的一种常用方法就是将该最优控制问题转化为Hamilton-Jacobi-Bellman方程,即
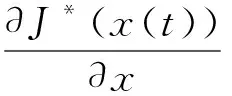
(13)
式中:J*(x)为一个值函数,其表达式为
(14)
若求解出Hamilton-Jacobi-Bellman方程,则最优控制量的表达式为
(15)
然而,对于非线性系统,得到Hamilton-Jacobi-Bellman方程的解析解是极其困难的,尤其是问题的维度比较高时[28-29]。随着人工智能技术的发展,上述问题的性能指标函数可采用策略梯度法进行优化[30]。
本文采用的是基于策略梯度下降的深度神经网络DDPG强化学习算法,该算法是一个不基于模型、在线、异步策略的强化学习方法。DDPG算法利用Actor-Critic神经网络来生成使长期回报最大化的最优动作。Actor网络基于当前的观测给出最佳动作,Critic网络基于当前的观测和动作给出奖励值估计。DDPG的观测量可以为连续或离散的,而动作空间是连续的。Critic网络并不需要评价所有动作来选出最佳动作,只关注当前Actor网络生成的动作。
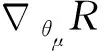
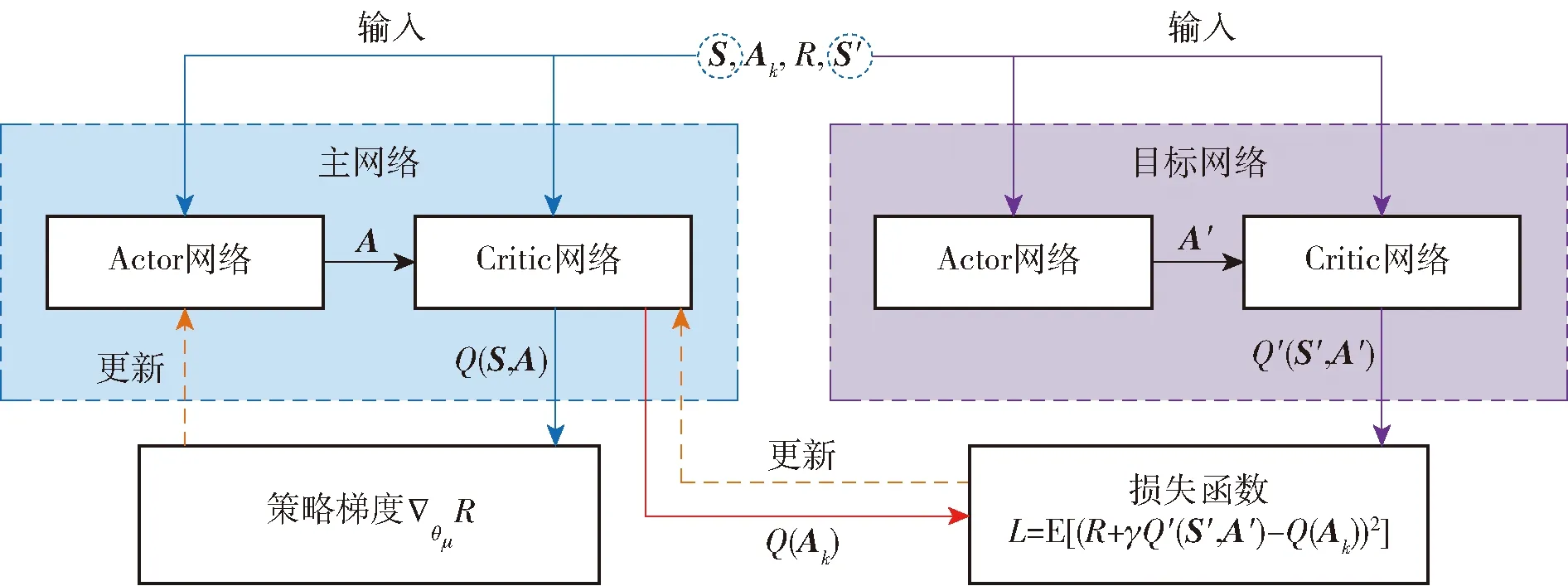
图2 DDPG算法的结构Fig.2 Structure of DDPG algorithm
2.2.1 状态空间设计
为实现多发导弹的协同打击,各发导弹的脱靶量要尽量小,且每发导弹的攻击时间要一致。因此,强化学习算法的状态空间设计为
S=[r1…ri…rnξ1…ξi…ξn]T.
(16)
2.2.2 动作空间设计
动作空间定义为制导律(7)式中的协同控制项,即
(17)

2.2.3 奖励函数设计
如1.3节所述,需要让脱靶量和剩余飞行时间的误差尽量小。当脱靶量小于1 m时,奖励值加10;且当剩余飞行时间误差小于0.02 s时,奖励值加10.因此,奖励函数设计为
(18)
2.2.4 行为策略设计
如图2所示,DDPG算法中包含了4个函数估计器,即:
1) Actor网络μ(S):输入为观测S,输出为使长期回报最大化的动作。
2) 目标Actor网络μ′(S′):为了提高优化的稳定性,算法基于最新的Actor网络参数值周期性地更新目标Actor网络。
3) Critic网络Q(S,A):输入为观测S和动作A,输出相应的长期回报的期望。
4) 目标Critic网络Q′(S′,A′):为了提高优化的稳定性,算法基于最新的Critic网络参数值周期性地更新目标Critic网络。
需要指出的是,μ(S)和μ′(S′)有相同的结构和参数,Q(S,A)和Q′(S,A)有相同的结构和参数。当训练结束时,训练好的最优策略存储于Actor网络μ(S)中。
DDPG算法的训练过程中会在每个步长都更新Actor网络和Critic网络,具体算法如下:
1) 用随机参数θQ初始化Critic网络Q(S,A),并用同样的参数初始化目标Critic网络Q′(S′,A′), 即θQ=θQ′.
2) 用随机参数θμ初始化Actor网络μ(S),并用同样的参数初始化目标Actor网络μ′(S′),即θμ=θμ′.
3) 对于训练中的每个步长:
(1) 对于当前的观测S,选择动作A=μ(S)+w,其中w为噪声模型中的随机噪声。
(2) 执行动作A.观测奖励R及后续的观测S′.
(3) 在经验池中存储经验(S,A,R,S′)。
(4) 从经验池中随机取出一小批M个经验(Sk,Ak,Rk,S′k),k=1,2,3,…,M.
(5) 如果S′k是最终状态,则设置值函数目标yi=Ri.否则,
yi=Ri+γQ′(S′k,μ′(S′k|θμ)|θQ′)。
(19)
值函数目标是经验奖励Rk和折扣未来回报的和。为了计算累计奖励,DDPG算法首先将后续的观测S′k从经验池中传到目标Actor网络来生成下一步的动作。然后算法将下一步的动作传到目标Critic网络得出累计奖励。
(6) 通过使经验值损失L最小化更新Critic网络参数:
(20)
(7) 利用下面的采样策略梯度使期望的折扣奖励最大化来更新Actor网络参数:
(21)
(22)
(23)
式中:Gai为Critic网络相对于Actor网络输出动作的梯度;Gμi为Actor网络输出动作相对于Actor网络参数的梯度。本文中,采用随机梯度下降法进行梯度更新。
(8) 基于如下目标网络参数更新方法来更新Actor和Critic网络参数:
① 平滑:每个时间步长利用平滑因子τ来更新目标网络参数,即:
目标Critic网络参数更新
θQ′=τθQ+(1-τ)θQ′;
(24)
目标Actor网络参数更新
θμ′=τθμ+(1-τ)θμ′.
(25)
② 周期性更新:不进行平滑处理时周期性地更新目标参数,即平滑因子τ=1.
③ 周期性平滑:周期性地更新目标参数,并进行平滑处理。
Actor网络和Critic网络在完成训练后,实际在线使用时,输入为弹目相对距离和剩余飞行时间估计的一致性误差,输出为2.1节(7)式中所涉及的协同控制项,从而实现多发导弹的协同制导。
3 仿真实验
3.1 决策优化
考虑交战场景中有2发不同初始条件的导弹和一个静止目标,决策优化过程中,交战场景的初始条件设置如表1所示。
如表1所示,导弹1和导弹2的初始位置和速度均不相同,目标垂直位置坐标随机从1 000 m、1 500 m、2 000 m中随机选取,这样导弹初始的航向角误差也会随着变化,使DDPG算法不会仅仅学习一条弹道,能够适应更广范围的交战初始条件。
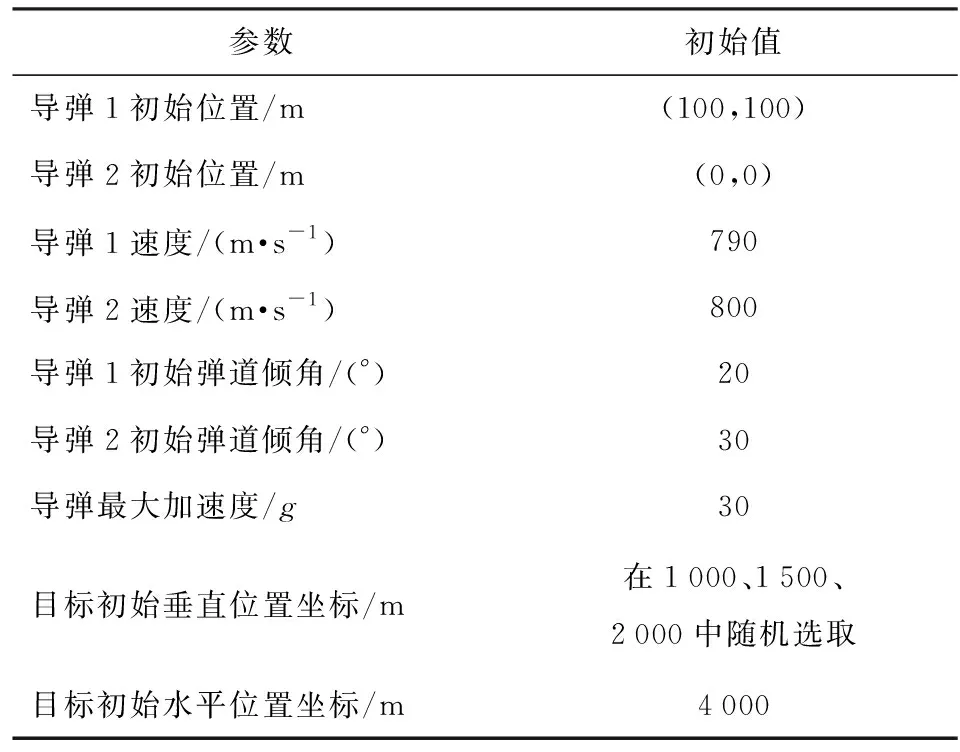
表1 决策优化的初始条件Tab.1 Initial conditions for policy optimation
DDPG算法训练过程中的Actor网络和Critic网络学习率分别设置为α1=0.000 1和α2=0.001,折算因子设置为γ=0.99.训练停止条件设置为训练次数达到915次。
训练过程中每次仿真的奖励值及最近5次仿真奖励值的平均值如图3所示。从图3中可以看到,随着训练的进行,奖励值波动上升,训练500次后,奖励值稳定在500左右,励值期望也在逐渐收敛。

图3 DDPG算法策略优化训练过程Fig.3 Training progress of policy optimation of DDPG algorithm
3.2 决策测试
算法测试过程中目标初始垂直坐标取为1 000~1 500 m,以0.5 m为间隔,进行1 000次仿真,统计每次交战的脱靶量及攻击时间误差,评价强化学习协同制导律的制导效果。
以目标垂直坐标为1 500 m为例,比例导引系数N=4,PN制导律、传统协同比例(CPN)制导律[7]、强化学习协同比例导引(RL-CPN)制导律的弹道如图4所示。由图4可见:PN制导律的弹道比较平滑,但是2发导弹的攻击时间分别为5.26 s和5.36 s,有0.1 s的差别,即未实现同时攻击;CPN制导律实现了2发导弹的同时攻击,攻击时间均为5.35 s,但弹道转弯次数较多,说明导弹在交战过程中不断调整制导指令来对齐剩余飞行时间;RL-CPN制导律为了实现同时打击,相应的弹道在制导初期开始进行必要的机动来对齐剩余飞行时间,转弯机动次数较少,最终2发导弹均在5.35 s实现了对目标的同时攻击。RL-CPN和CPN制导律的指令加速度如图 5所示,可见在交战结束时,制导指令并没有饱和,因此导弹有能力精确命中目标。但本文中奖励函数未考虑燃料消耗,因此RL-CPN制导律的制导指令幅值较大,在后续工作中需要进一步探索燃料最优的RL-CPN制导律。
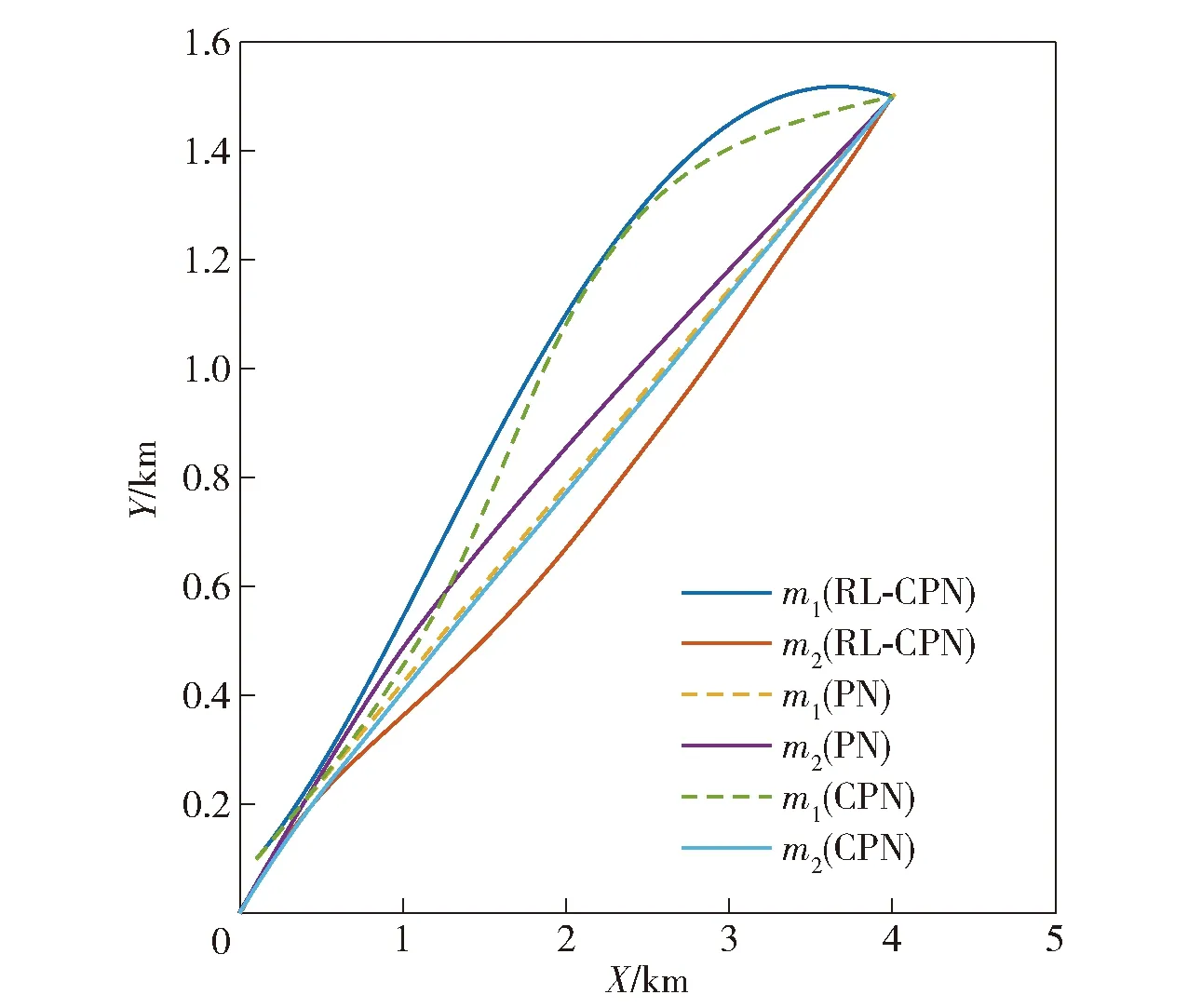
图4 二维协同打击的弹道对比Fig.4 Comparative trajectories of 2-D engagement
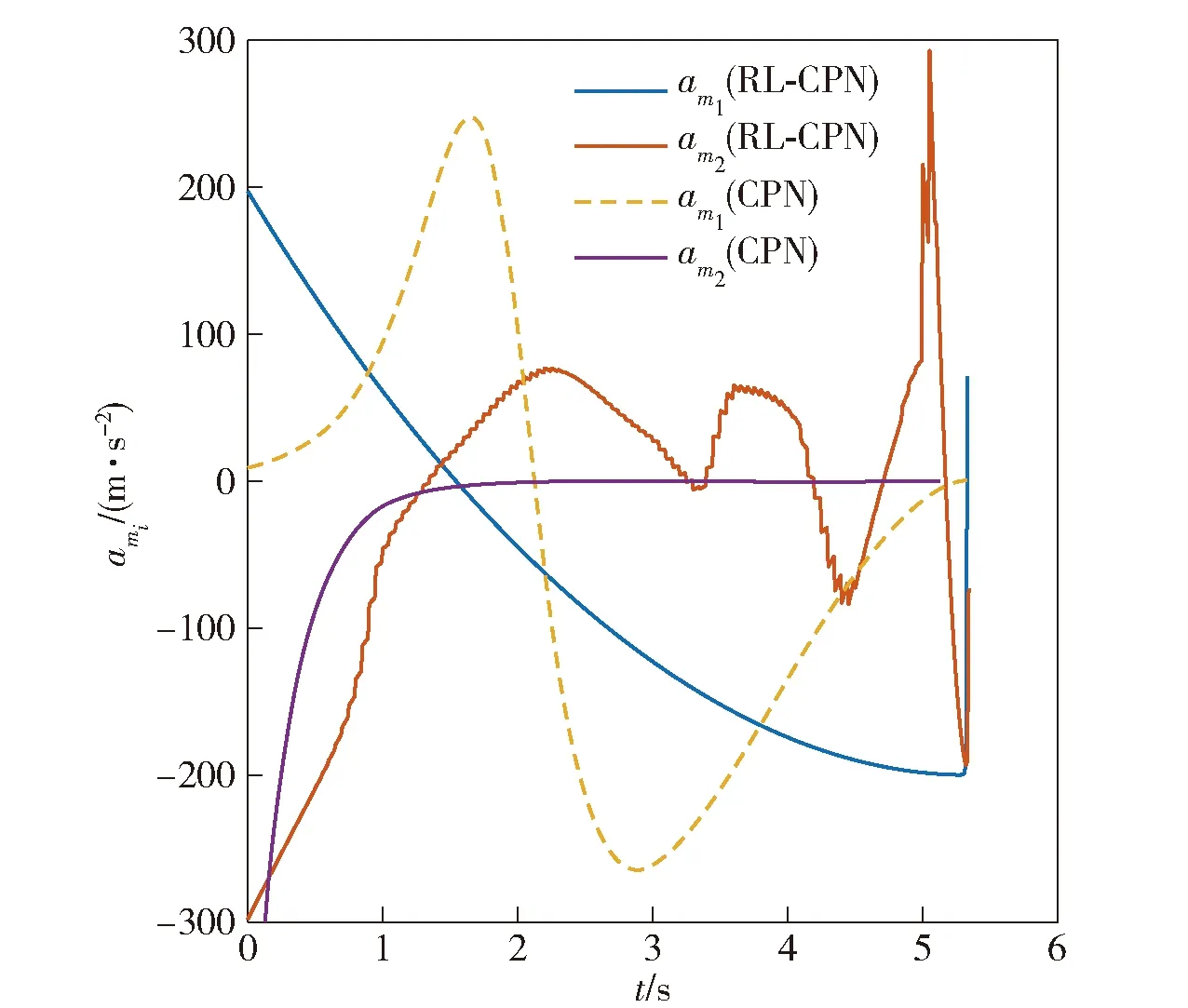
图5 RL-CPN和CPN制导律的导弹指令加速度Fig.5 Commands acceleration of CPN and RL-CPN
1 000次仿真的统计结果如表2所示。从表2中可以看出:RL-CPN制导律的攻击时间误差平均值为0.001 s,而PN制导律的攻击时间误差为0.101 219 8 s,二者相差了两个数量级;与CPN制导律相比,RL-CPN制导律的脱靶量和攻击时间误差也相对较小,也就是说,RL-CPN制导律的制导精度更高。

表2 制导律性能的对比Tab.2 Comparation of guidance laws
3.3 拓展交战场景下的决策测试
为了进一步验证RL-CPN制导律的有效性,本文一些未在训练中使用的数据将用来进行测试。设置目标垂直位置2 000~2 500 m,以0.5 m为间隔,进行1 000次仿真,统计每次交战的脱靶量及攻击时间误差,评价RL-CPN制导律的制导效果。
仿真结果如表3所示,从中可见RL-CPN制导律的脱靶量依然小于PN制导律和CPN制导律的脱靶量。此外,RL-CPN制导律的脱靶量标准差也比PN制导律和CPN制导律的小,说明RL-CPN制导律的性能更加稳定。RL-CPN制导律的攻击时间误差为0.006 239 s,依然较PN制导律的小一个量级。尽管RL-CPN制导律的攻击时间误差在本仿真场景中略大于CPN制导律,但是其脱靶量仅为CPN制导律的约1/3,对于同时打击而言更具有实战意义。

表3 拓展交战场景进行制导律性能的对比Tab.3 Comparation of guidance laws in extended engagement scenarios
图6、图7、图8分别为对RL-CPN制导律、CPN制导律和PN制导律的脱靶量进行了直方图统计。由图6、图7、图8可以看出:RL-CPN制导律脱靶量集中在0~1 m;而PN制导律的分布则比较均匀,出现较大脱靶量的次数更多;CPN制导律的脱靶量在3.5~4.0 m区间出现的频次则更多,这也说明了RL-CPN制导律的制导精度更高。这是因为本文所考虑的是非线性交战动力学模型,剩余飞行时间的估计和制导律的设计不再基于文献[7]所考虑小角度假设下的线性动力学模型。强化学习算法中的神经网络理论上可以拟合任何非线性函数,因此本文制导律可获得较高的制导精度。

图6 RL-CPN制导律的统计直方图Fig.6 Miss distance histogram of RL-CPN
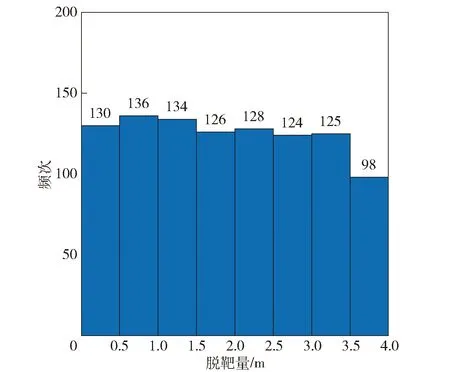
图7 CPN制导律的统计直方图Fig.7 Miss distance histogram of CPN

图8 PN制导律的统计直方图Fig.8 Miss distance histogram of PN
另外,考虑目标运动状态的不确定性也是一项值得研究的工作。若考虑目标机动的不确定性,强化学习算法在训练时就要给定一些目标机动的场景,如目标做常值机动、Bang-Bang机动、正弦机动等,随机选取机动幅值的大小和频率来构造训练环境,算法收敛后,令目标执行一些训练未遇到的机动幅度大小和频率,对算法进行测试。最后,结合仿真结果来评价考虑目标机动的不确定性时强化学习协同制导律的效果。
4 结论
本文设计了一种基于强化学习算法的协同制导律,可以实现多发导弹对目标的同时打击。通过仿真实验,得出主要结论如下:
1) RL-CPN制导律实现了分布式协同,不再需要提前指定某攻击时刻,而是各发导弹根据剩余飞行时间误差这一协调变量生成制导指令,进而实现剩余飞行时间的一致性,达到同时打击的目的。利用图论理论,各发导弹不需要“弹群”的全局信息,只需与其邻居进行通讯,降低了通讯负担。
2) RL-CPN制导律脱靶量较小,各发导弹之间的剩余飞行时间误差较小,制导精度高,能够适应线下学习未训练的交战场景。
3) 基于强化学习算法设计制导律,极大简化了制导律设计过程,无需考虑控制器的结构,也免去了控制器的调参过程,缩短了制导律的设计周期。
4) 由于未考虑导弹的燃料消耗因素,RL-CPN制导律燃料消耗较大,在后续工作中可以进一步优化。
本文后续工作可进一步拓展智能协同制导的应用场景,考虑导弹速度是时变的以及导弹轴向速度可控的情况,以提高多弹同时攻击的制导精度。此外,可将本文方法扩展为三维协同制导,除考虑燃料消耗最优需求外,也可考虑攻击角度约束及避障、避撞等约束,实现多发导弹在多约束条件下的智能协同制导。

