基于DEMON谱和LSTM网络的水下运动目标噪声基频检测∗
卢佳敏 宋三明 景 严 张 瑶 谷 浪鲁 帆 胡志强 李 硕
(1 中国科学院沈阳自动化研究所 机器人学国家重点实验室 沈阳 110016)
(2 中国科学院机器人与智能制造创新研究院 沈阳 110169)
(3 中国科学院大学 北京 100049)
(4 中国科学院声学研究所 北京 100190)
0 引言
水中机动目标在航行时会辐射出具有特殊频谱分布的噪声,因此可以通过噪声分析来估计航行器的吨位、桨叶数等物理特征和轴频、航速等运动状态[1−2],进而实现合作或对抗场景下的态势感知。轴频是螺旋桨转速的最直接反映[3],对水下目标探测具有重要的意义,本文将重点研究如何从水听器阵列接收到的噪声中估计轴频信息。
轴频也称为基频,在数值上等于目标螺旋桨主轴的转动频率[4],常用DEMON 谱分析法提取调制谱特征,以获取基频及其谐波在内的低频线谱,进而检测目标的基频、叶频或桨叶数目。文献[5–6]评估了不同解调分量得到的DEMON谱的鉴别能力。文献[7–11]研究了DEMON 谱净化与增强,提高了线谱的信噪比与基频估计的精度。其中,文献[7]基于线谱之间的倍频关系,提出基于最大公约数的基频提取方法,文献[12–13]对此进行了拓展并提出相应的改进方法。这些算法需要人为设置参数进行特征提取和基频估计,对信噪比较敏感。实际接收到的目标噪声信号,受到不同海洋波导传输过程的乘性作用和加性干扰,其信噪比变化大[14−15]。
深度学习具有较强的泛化能力,近年来逐渐被研究人员引入水下目标识别领域。文献[16]通过提取DEMON 谱中各谐波之间的结构特征关系建立模板库,根据模板库对深度神经网络(Deep neural networks,DNN)进行训练,并识别螺旋桨的叶片数目。文献[17]将梅尔频率倒谱系数(Melfrequency cepstrum coefficient,MFCC)和频谱包络特征输入卷积神经网络(Convolutional neural networks,CNN)和深度置信网络(Deep belief networks,DBN),对船舶目标进行分类。文献[18]提出一个类似方案,将线性预测倒谱系数(Linear predictive cepstral coefficient,LPCC)和MFCC 串联后输入DBN 网络。文献[19]将梅尔频率特征分别输入支持向量机(Support vector machine,SVM)和VGGish 网络中,对生物、潜艇和船只3 种目标噪声进行分类。文献[20]使用堆叠降噪自编码器(Stacked denoising auto encoder,SDAE)对原始信号数据进行降维和逐层特征提取,然后使用SVM和BP 网络进行分类。文献[21]开展了基于长短时记忆(Long short-term memory,LSTM)网络的声学目标分类,发现时域、频域和MFCC 三种特征具有相当的分类性能。随后,他们对DEMON 谱和MFCC等特征进行融合,提高了LSTM 网络的分类准确率[22]。
大多数现有水下目标分类算法首先通过波束形成将水听器阵列信号约减为一维信号,然后提取频域特征输入深度网络进行训练。本文开展基于深度学习的基频估计,但是重点考虑如下两个问题:
(1)在特征提取时,绝大多数研究都采用了MFCC特征。MFCC反映能量在不同频率区间的分布,本质上是对噪声信号频谱包络的一种描述,关注的是连续谱而非调制谱特征。
(2)在波束形成时,会丢失很多细节信息,且会引入新的阵形估计误差。
对于问题(1),由于调制谱是由基频及其谐频决定的,而一般采用DEMON 谱来提取调制谱,所以本文在估计基频时候选择DEMON 谱作为网络的输入。需要注意的是,在目标航速很低时噪声的调制效应很弱,因此调制谱分析更适合分析非低速航行下的目标噪声。
对于问题(2),一种更加合理的选择是将水听器阵列采集的多通道信号直接用于特征提取。然而,多通道数据不仅会导致特征数急速增长,而且还会引入随机噪声的谱特征。本文拟采用CNN 网络对多通道特征进行二次特征提取,实现特征降维和净化。最后,将多个时间窗对应的二次特征输入LSTM网络实现基频估计。
1 算法流程
本文提出的基频检测算法流程如图1所示。首先,对每个通道的噪声信号作加窗分帧处理,在每个时间窗内提取DEMON 谱特征;然后,利用梳状滤波器对DEMON 谱特征中包含的倍频关系进行增强;最后,将同一时间窗内所有通道特征组成二维矩阵经卷积层处理后输入LSTM网络。
本文采用分类网络来估计基频。把基频取值范围分成几个频段,每个频段当作一个类别,将基频估计问题转化为分类问题。需要说明的是,也可以采用回归网络进行基频估计。但是,在很多研究领域中,回归网络或者分类网络在性能上并不存在本质的区别[23−24]。下面将详细介绍算法各个步骤的具体实现方法。
1.1 DEMON谱
DEMON谱的计算流程如图2所示。

图2 DEMON 谱计算流程图Fig.2 The DEMON spectrum extraction procedure
调制信号对不同频带噪声的信号调制强度是不同的[7]。可以将信号的频谱划分成多个频段,然后将不同频段的线谱进行融合来提高线谱质量。具体包括如下几个步骤:(1)在高频端选取若干个子带,对原始噪声信号进行时域带通滤波;(1)对每个子带进行平方解调,得到时域包络;(2)对包络做快速傅里叶变换(Fast Fourier transform,FFT)得到频谱,并利用双向α滤波器去除趋势项得到各个子带的线谱;(3)根据线谱根数将各子带的线谱进行加权融合,得到最终的线谱特征。考虑到水中运动目标的实际工况,后面实验中将基频的搜索范围限制在5~10 Hz之间。而且,由于DEMON谱的线谱阶数不会太高[7],本文以10 阶为限,仅保留100 Hz以下的DEMON谱。
1.2 梳状滤波器
受到不稳定调制的影响,线谱之间的倍频关系可能会减弱或消失。本文采用文献[25]提出的梳状滤波器对倍频关系进行增强。梳状滤波器由许多按等频率间隔排列的通带和阻带组成,能够很好地保留信号中的倍频关系。
对于理想的DEMON 谱,其对数频域上基频及倍频的分布可以表示为
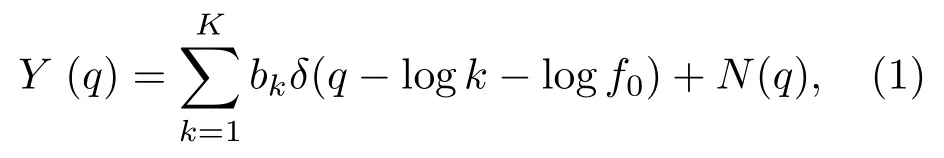
其中,b为线谱幅度,k表示第k个谐频,f0为基频,N(q)为加性噪声。
理想状态下,各次谐波线谱之间遵守严格的倍数关系。当梳状滤波器h(q)的第一个通带移动至某个线谱频率处时,其余各通带会落在该频率对应的各次谐波上,对各个谐频进行累积。在第一个通带位于基频f0处时达到峰值。相应的理想滤波器h(q)可以用式(2)描述:

但在实际中,基频及谐频之间的倍频关系并不严格,如谐频位置存在偏差或存在一定的谱峰宽度。因此,DEMON 谱不能直接用式(1)描述,相应的也不能用式(2)的滤波器进行滤波。一种考虑了偏差和谱峰宽度的滤波器为
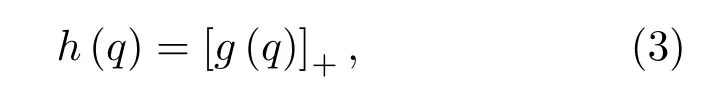
其中,g(q)为

参数K是谐波个数,γ代表谱峰宽度。在后面的实验中K取10,γ取1.8,取β,使
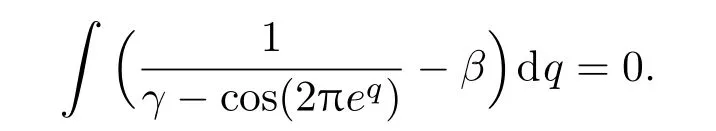
利用梳状滤波器进行滤波时,首先将特征信号映射至对数域,q=logf,然后将DEMON谱与滤波器做卷积得到增强后的线谱特征:
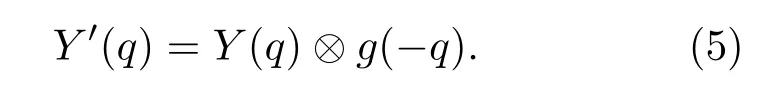
梳状滤波前后的DEMON 谱如图3所示,滤波后谐波结构(线谱间的倍频关系)明显增强。
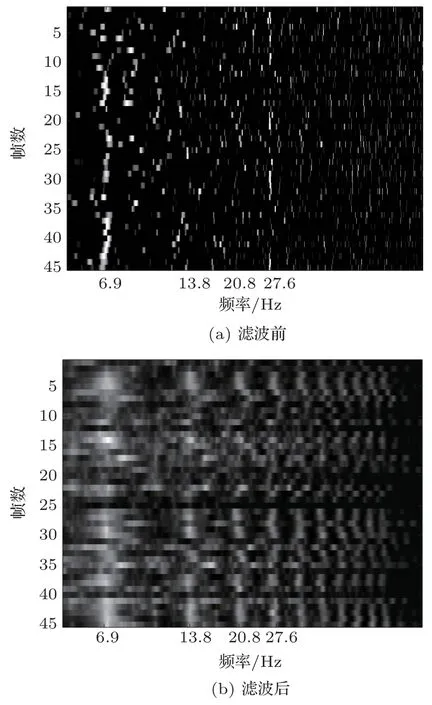
图3 梳状滤波器对DEMON 谱的增强效果Fig.3 Enhancement to DEMON spectrum by the comb filtering
1.3 深度分类网络
提取DEMON 谱特征后,可以通过训练分类网络来估计基频。作者在文献[26]中提出过一种基于CNN 网络的检测方法,利用小波变换对DEMON谱特征去噪,然后将将净化谱特征输入CNN 网络来估计基频。但是,去噪可能会造成谱特征信息的丢失,而且单纯采用CNN 网络需要对较长的时间序列进行融合,影响实时性。本文去掉了去噪步骤,同时在CNN 网络上增加了LSTM 网络,以期利用LSTM 网络的时序建模能力去捕获低信噪比条件下基频及其倍频的统计特性,提高基频估计的稳定性和实时性。
LSTM是循环神经网络(Recurrent neural network,RNN)的一种改进结构,具有RNN 处理时间序列信号能力的同时解决了RNN 存在的长时依赖问题,被广泛用于处理各种语声任务。LSTM 基本单元结构如图4所示。其中,xt为各时间步输入LSTM 单元的特征,ht是各时间步LSTM 单元的输出,sig为sigmoid函数。
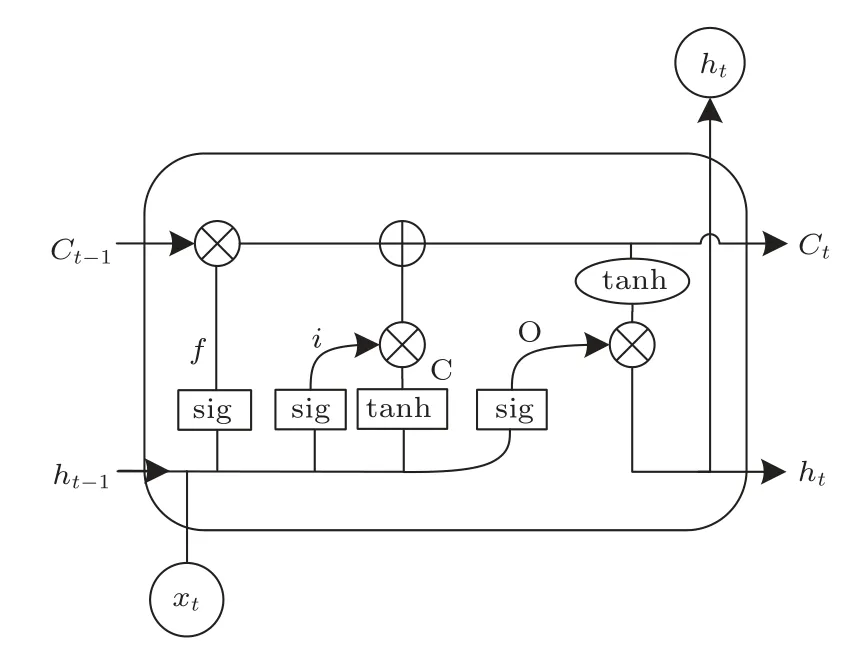
图4 LSTM 基本单元Fig.4 Cell of LSTM
网络的整体结构如图5所示,包含一个拥有8个3×3 卷积核的卷积层、一个卷积核尺寸为2×2的池化层、一个含有256 个神经元的LSTM 层以及一个大小为128的隐藏层和大小为25的softmax 分类层。注意,输出是one-hot 向量,当基频的真实值落在相应频率范围内时,该类值为1,其余为0。损失函数采用交叉熵函数,网络使用mini-batch 进行训练。其中卷积层对输入的多通道DEMON谱特征进行降维,LSTM层用于提取输入信号的时序特征,随后输入分类网络进行分类。
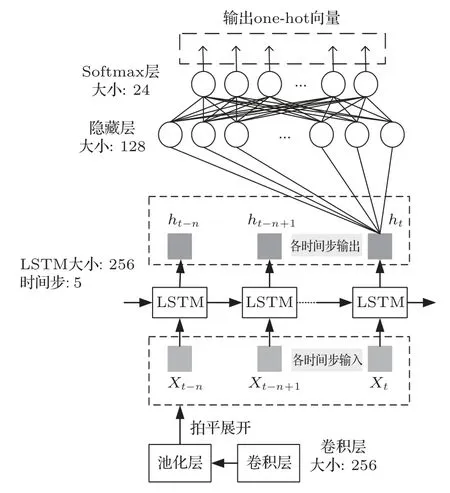
图5 网络结构示意图Fig.5 The proposed deep-learning network structure
2 数据仿真
训练深度网络需要大量标定好的数据。但是,真实舰船噪声数据往往比较稀缺,而且实测数据标定是一项繁琐且容易出错的工作。因此本文首先使用仿真数据对网络进行训练,在湖试中利用实测舰船噪声数据对预训练好的网络进行微调后,再进行基频估计。本节介绍舰船噪声信号的仿真方法。
对于仿真舰船噪声信号来说,周期性局部平稳过程[14]和准周期性随机声脉冲序列模型[15]是描述其时域信号较为客观接近实际的两种数理模型。准周期性随机声脉冲序列模型可以模拟以不同噪声源为主导的不同工况下的目标辐射噪声信号,其脉冲形状和脉冲出现的周期性程度可取不同值,使其具有不同的宽带连续谱形状和不同线谱幅度、调制深度,具有良好的普适性,因此本文根据文献[15]对目标噪声信号进行仿真。
2.1 舰船噪声准周期性随机声脉冲序列模型
舰船噪声的频谱可以看作由连续谱和线谱叠加组成,噪声的时域波形可以看作由准周期性随机脉冲声序列构成,其中第n个声脉冲的出现时刻(脉冲前沿)为

其中,T为声脉冲序列之间的平均间隔,Δn为脉冲序列在周期点附近的随机摆幅,服从均值为零、方差为δΔ的正态分布。
准周期性随机声脉冲序列指出噪声辐射线谱相对于连续谱的幅值仅取决于脉冲的随机摆幅,脉冲序列的准周期性越差,则线谱幅值越低。对于不同工况的船舶,通过选择周期性随机序列脉冲的各个参数可以获得不同频率和幅度的线谱,以及谱峰频率不同、连续谱形状和衰减规律不同的功率谱[15]。
以声脉冲形状为指数衰减型为例给出具体实现过程。第n个声脉冲的形状为[15]


其中,γ为衰减系数,τ是脉冲持续时间。脉冲幅度分布遵循式(9):
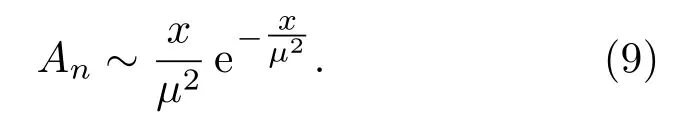
每个脉冲的起始时间在桨叶周期附近服从高斯分布:

图6给出一段仿真信号的频谱。

图6 一段基频为5 Hz 的噪声仿真信号的频谱Fig.6 The frequency spectrum of a synthesized ship-radiated noise signal with the shaft frequency being 5 Hz
2.2 阵列信号仿真
海洋环境噪声和水声信道传输过程会降低接收点处接收信号的信噪比,本节介绍如何仿真受海洋环境影响的接收点信号。
本文主要面向接收点与目标之间距离为中近距离的情形,侧重考虑随距离变化的声能平均传播损失、海底与海面反射引起的相干多途干扰以及海洋环境噪声加性干扰。采用基于射线声学的bellhop模型对传播损失和多途干扰进行仿真,声源深度10 m,接收6 元阵,接收深度10 m,为垂直线阵,接收阵水平距离2000 m,海水密度1.0 g/cm3,海底声速1680 m/s,海底密度1.8 g/cm3,吸收系数0.6 dB/λ。声速剖面分别选用等声速梯度剖面、负声速梯度剖面、含有温跃层的浅海声速剖面、深海Munk 声速剖面等,水深分别选用50 m、500 m、5000 m,来模拟不同环境下的相干多途传播信道。声源使用2.1 节中合成的仿真信号。海洋环境噪声使用不同信噪比高斯白噪声模拟。
合成的仿真噪声数据与真实工况下的噪声并不完全一致,但可以使用仿真数据完成网络训练后,再利用真实数据对网络进行微调来弥补二者之间的差别。
3 实验结果及分析
本文设计了4个实验来测试本文提出的基频检测算法。
(1)分别采用本文提出的深度学习算法(数据驱动)和传统的模型驱动方法对仿真噪声信号进行基频检测,以测试数据驱动方法在抗噪性和适应性上的提升。
(2)本文在文献[26]的基础上,去掉了去噪步骤,增加了LSTM网络。为此,本文设计了一组对比实验来比较二者在准确性和实时性上的性能差异。
(3)为了测试LSTM 网络在提取时序谱特征上的可行性,分别采用CNN 和CNN+LSTM 网络开展时序基频检测。实验中保持两者卷积层部分的结构相同。
(4)分别采用本文提出的深度学习算法(数据驱动)和传统的模型驱动方法对外场实测噪声数据进行基频检测,以测试本文方法在实测数据上的检测性能。
在仿真数据准备阶段,总共生成了长度大约为12 h 的数据,采样频率为10 kHz,数据的基频范围在5~10 Hz 之间,按0.2 Hz 的间隔划分为25 个类别。估计的基频值定义为预测类别的中点。例如:划分到5~5.2 Hz 类别的基频预测值为5.1 Hz。仿真的噪声数据中桨叶数的取值为3~7 叶。此外,本文将80%的样本作为训练数据集,剩余20%的数据作为测试样本集。评价指标包括:P,定义为误差小于0.1 Hz 的预测值比例,计算公式为P=(N −Ne)/N ×100%,其中Ne为预测误差超过0.1 Hz 的数据个数,N为总数据量;平均误差,其中fig表示第i段数据的真实基频值,fip表示第i段数据的预测基频值。
3.1 数据驱动方法与模型驱动方法
传统检测方法存在对先验知识的依赖,尤其DEMON 谱提取过程和倍频统计步骤需要人工设定很多参数。本文方法简化预处理过程,并利用神经网络建模的方式降低检测算法对先验知识的依赖。为了比较两类方法的性能,本文选取文献[12]和文献[13]中提出的两种基于DEMON 谱的基频提取算法作为对比。这两种方法计算基频时,首先利用波束形成将阵列信号约减为一维信号,再进行计算。
表1 给出了两种不同信噪比(Signal to noise ratio,SNR)背景噪声强度下对仿真数据进行基频检测的结果,两种模型驱动算法的检测性能相当,而本文方法在误差小于0.1 Hz 的预测值比例P上有较大提升,且平均误差更小。相对于传统方法从DEMON 谱提取人工特征然后计算基频而言,基于深度网络的方法提取DEMON 谱的高层特征再进行基频估计,能够降低噪声的影响,从而改善检测结果。而传统方法提取的浅层特征对噪声线谱的抗干扰能力相对较弱,因此对于SNR 较低、线谱质量较差的DEMON 谱,本文方法能够取得较常规方法更好的检测结果。但是,当DEMON谱质量较好,干扰线谱很少的时候,常规方法也能获得比较理想的检测结果。
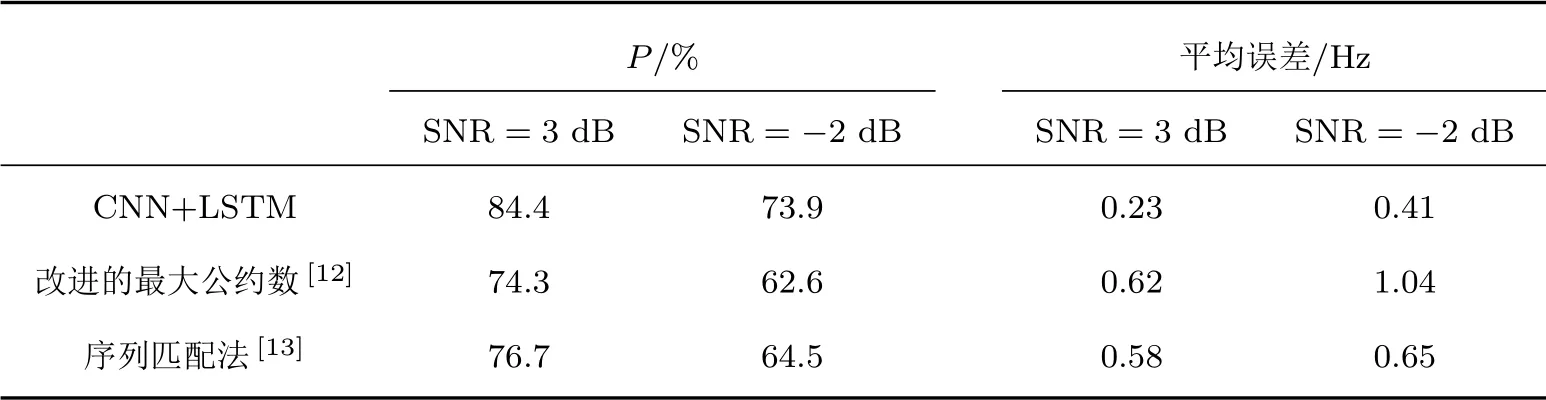
表1 本文方法与传统方法的对比结果Table 1 Comparison between classic methods and the proposed method
3.2 本文算法与文献[26]的检测结果对比
文献[26]提出了一种基于CNN 网络的基频检测方法。而本文优化了网络结构,去掉了DEMON谱去噪和多帧融合步骤,使得特征提取部分更加简单。两种方法的检测结果对比如表2所示。
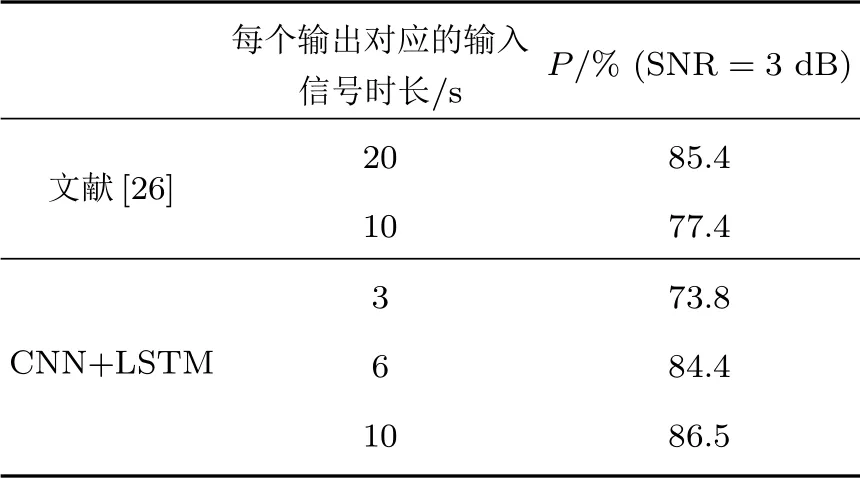
表2 与文献[26]进行对比Table 2 Comparison with the method in Ref.[26]
从表2 可以看出,当信号输入时长上由20 s 下降至6 s 时,本文的检测算法几乎达到同样的准确率;而输入时长增加至10 s时,误差小于0.1 Hz的预测值比例P会略高于CNN网络。因此,尽管简化了预处理程序,但是LSTM 网络却能够以较短的信号输入时长获得大致相同的P值;从不同时长的检测结果能够看出,本文的方法在时效性上有了较大的提升。对于本文提出的算法,对比时长为3 s 和6 s的实验结果,可以发现时长较长的信号能够提供更多稳定的检测结果。由于计算代价和信号长度成正比,这也提示我们可以通过调整输入信号的时长来满足不同任务对准确率和实时性的不同需求。
3.3 CNN 和CNN+LSTM的检测结果对比
为了验证LSTM 网络从时序DEMON 谱中提取统计特征的能力,分别采用CNN和CNN+LSTM网络进行基频检测。表3 列出了两种网络结构在不同的输入信号长度上的实验结果。CNN 的输入为一帧语音信号计算的DEMON谱,添加LSTM层的网络每输入5 个时间帧输出一个检测结果,其中帧间重叠为50%。

表3 CNN 与CNN+LSTM 的实验结果对比Table 3 Comparison between CNN and CNN + LSTM
当帧长为1 s时,CNN网络的P值在53%左右,添加LSTM 结构后增加至74%;当帧长增加至2 s时,前者的P值上升至75%左右,而后者提高至84%左右。由实验结果能够看出,随着帧长的增加,输入网络的特征信息将增多,基频的检测精度上升;而在相同的帧长情况下,添加LSTM 层后精度有较大的提升,表明LSTM 网络能够较大幅度提升基频检测的准确率。
3.4 外场实验数据分析
分别利用湖试数据和海试数据对所提算法进行测试。其中,湖试数据于千岛湖外场实验中获得,目标船只吨位为几十吨级,接收距离约1 km,共采集216 段数据;海试数据于三亚外场实验中获得,为百吨级渔船噪声,接收距离约2 km,共采集162段数据。两次实验的接收阵均为24 阵元的水平线阵,阵元距离1.875 m,位于水下15 m,采样频率为20 kHz。数据共包含5 种不同转速,基频范围为5~10 Hz。对使用湖试数据进行基频估计前,先利用实测噪声数据对神经网络的权值进行微调学习。为了扩充数据集,本文采用加噪、平移、缩放等方式对实测数据进行数据集扩充。使用20%的数据作为训练集,其余80%数据作为测试集。
将无目标情况下采集到的背景噪声放大后叠加到原始信号上,叠加后信号的信噪比大约为0 dB,用于验证加噪情况下算法的性能。
表4 给出了两组外场实验数据的基频检测结果。其中原始数据中目标距离较近,信号的信噪比相对较高。因此,本文方法及常规基频检测方法均获得了较好的检测结果,但本文方法的平均误差更小。对于加噪后的信号,本文方法较常规方法在精度上有较大的提升,并且平均误差在可接受的范围;常规方法的精度较低且常出现倍频半频错误的缘故导致平均误差很大。
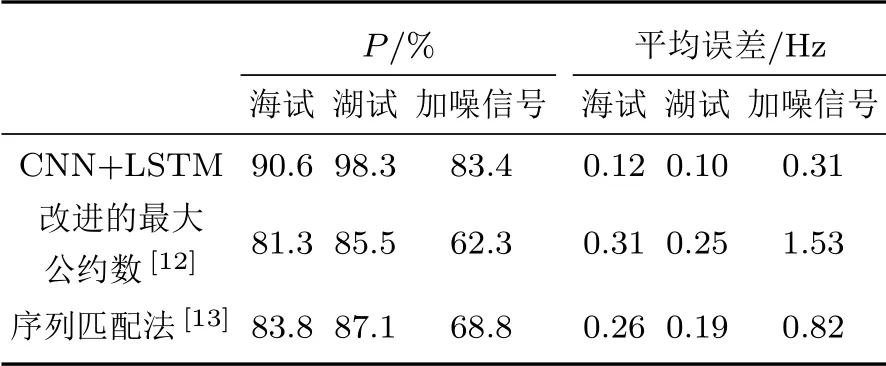
表4 本文方法与传统方法在实测数据上的检测性能对比Table 4 Comparison between classic methods and the proposed method on the field dataset
图7 给出了一段实测噪声的时域波形及其DEMON 谱,从DEMON 谱中能够看到较多的干扰线谱。表5 给出了该段数据分别使用3 种方法得到的检测结果。可以看到,常规方法由于受到干扰线谱的影响,估计出的基频值误差较大。
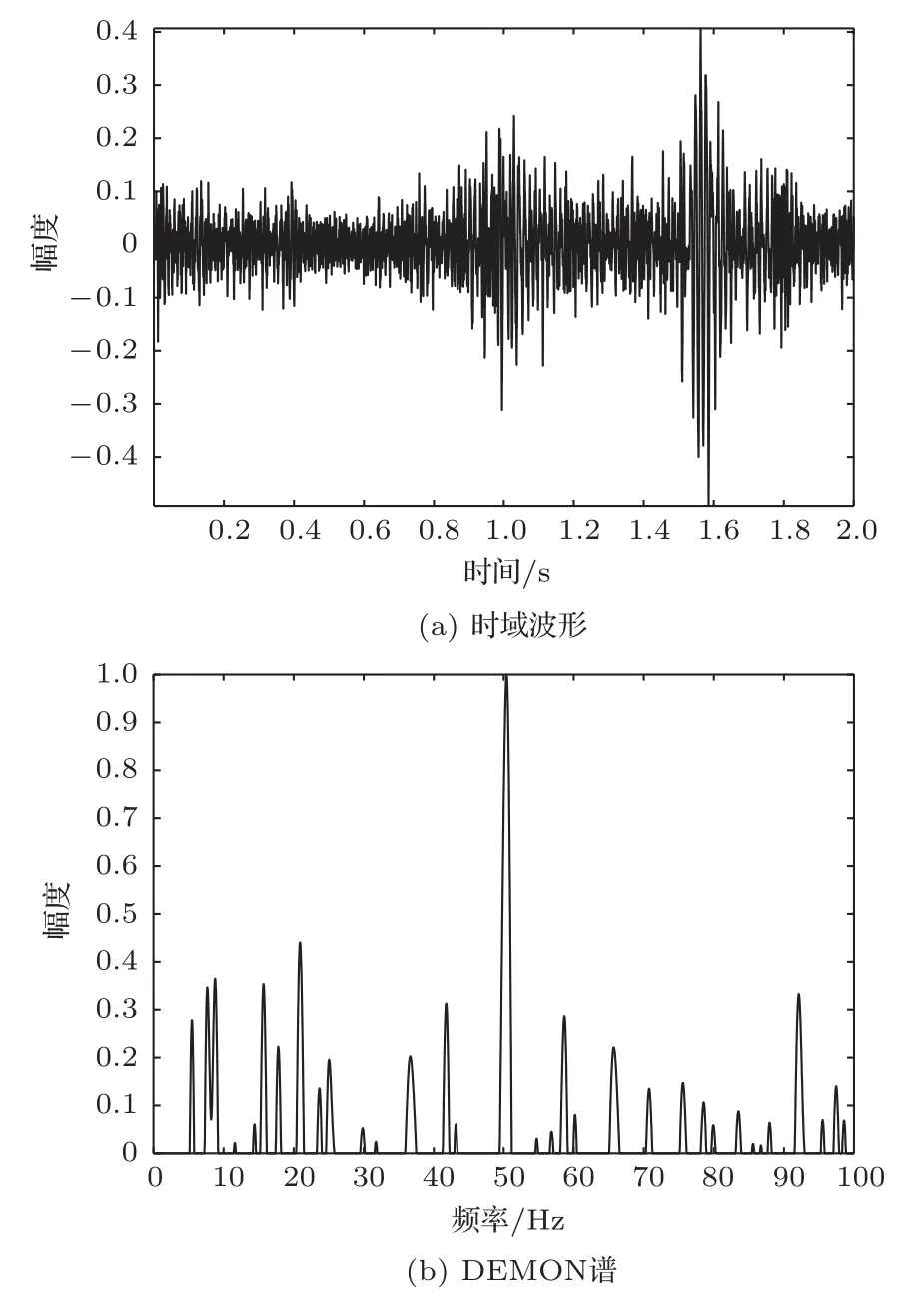
图7 某段基频为8.4 Hz 的渔船噪声数据Fig.7 A segment of sea trial data with shaft frequency being 8.4 Hz

表5 图7 的基频检测结果Table 5 Fundamental frequency detection results of the signal segment in Fig.7
4 结论
本文提出了一种基于CNN 和LSTM 网络的水下目标辐射噪声基频检测方法。在网络输入上,与传统方法利用波束形成融合多通道信息不同,本文提取每个通道的DEMON 谱并以二维矩阵的方式直接送入网络中,充分利用各个通道的信息;在特征提取部分,去掉了先前工作中的去噪和多帧融合步骤,在简化预处理步骤的同时提高算法的实时性,也摆脱了传统模型驱动算法在预处理过程中对先验知识的依赖。最后,将经过CNN+LSTM 提取的特征输入全连接层实现基频估计。仿真实验和实验数据表明,本文方法能够较好适应模拟的不同环境和不同信噪比的目标噪声,具有良好泛化性能,可望实际推广;在一定信噪比下,能够从时序DEMON 谱特征中估计出较为准确的基频值,可供进一步研究和应用参考。
需要注意的是,本文主要关注较高航速下目标噪声的基频检测。当航行速度很低时,无法从DEMON 谱中提取到基频的调制信息,所以本文算法不适用于低速状态的航行器的基频检测。且限于实测数据规模的限制,本文使用仿真数据进行训练。仿真数据并不能完好地模拟实测数据,因此对实测数据的检测结果可能有一定的影响。后续工作中随着实测数据数量的增加,将尽可能利用实测数据对网络进行训练,进一步提高网络的性能。

