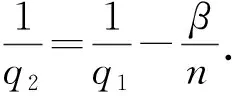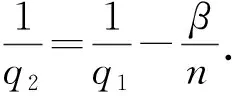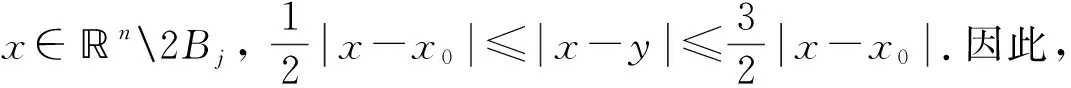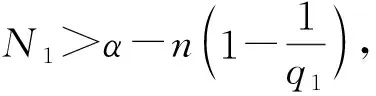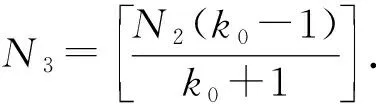与高阶Schrödinger型算子相关的变分算子的Lipschitz交换子
孟晓燕, 赵 凯
(1. 青岛黄海学院 数学教学部, 山东 青岛 266427; 2. 青岛大学 数学与统计学院, 山东 青岛 266071)
1 预备知识
设非负位势V属于反向Hölder类RHq(q>1), 即存在q0>1和常数C>0, 使得对任意n中的球B, 有
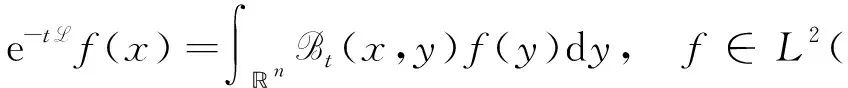
其中热半群e-tL的核B满足
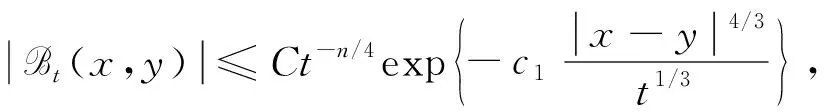
(1)
式中C和c1均为常数.
定义1[16]设{ti}i∈是正的单调减趋于零的数列, 令ρ>2, 则与高阶Schrödinger型算子L生成的热半群相关的变分算子定义为
这里上确界取遍所有正的单调减趋于零的数列{ti}i∈.
下面给出与高阶Schrödinger型算子相关的变分算子Vρ(e-tL)及Lipschitz函数b构成的交换子定义, 其中Lipschitz函数是满足如下条件的函数:
此时称f属于Lipβ(n).
定义2设Vρ(e-tL)是与高阶Schrödinger型算子相关的变分算子,b∈Lipβ(n), 则变分算子Vρ(e-tL)和b构成的交换子定义为
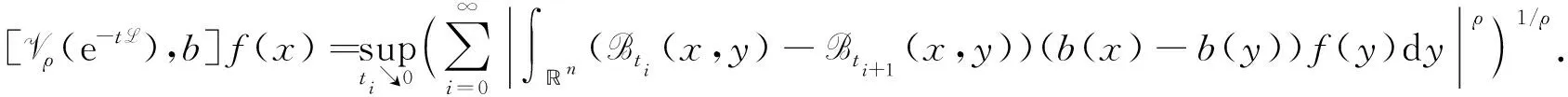
(2)
为方便, 下面给出辅助函数γ(x)的定义和性质[17].定义
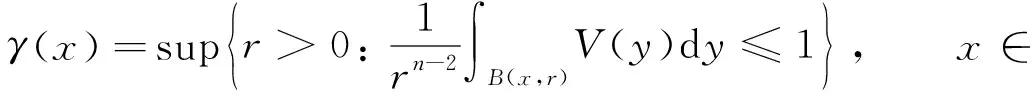
引理1[17]设V∈RHn/2(n), 则存在常数C和k0>1, 使得对所有的x,y∈n, 均有
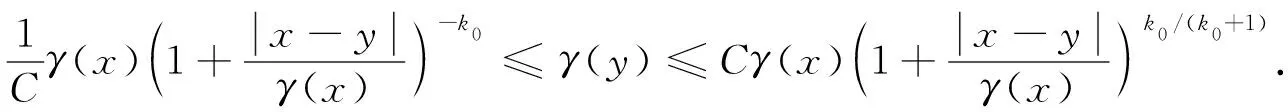
(3)
特别地, 当|x-y| 引理2[16]对任意N∈, 存在正常数C,c2和c3, 使得对所有的x,y∈n和0 对于整数k, 记Bk={x∈n: |x-x0|<2k},Ck=BkBk-1, 且χk=χCk.文献[1-2]给出了齐型Herz空间及Herz型Hardy空间的概念和主要结果. 定义3[2]令-∞<α<∞, 0 其中 1) suppa⊂B(x0,r),r>0; 2) ‖a‖Lq(n)≤; 则称a(x)为一中心(α,q)-原子. (4) 这里下确界取遍f的所有分解. 定义5[3]设α∈, 0 其中 ‖Iβ(f)‖Lq2(n)≤C‖f‖Lq1(n),f∈Lq1(n), (5) 先证明如下关于变分算子交换子[Vρ(e-tL),b]的Lq有界性. 证明: 对任意f∈Lq1(n), 由其定义及引理2, 有 由式(5), 可得 证毕. 下面给出本文的主要结果. 对于J2, 下面分两种情形讨论. 1) 当0 2) 当1 1) 当|x-x0|≤γ(x0)时, 由其定义和引理2知, 由Hölder不等式和原子的大小条件得 从而 当1 2) 当|x-x0|>γ(x0)时, 由其定义和引理2, 并利用式(3)知, 同理可分为0 因此 证毕. 对于U2, 由式(6), 即变分算子交换子的Lq有界性, 有 再由 (9) 并注意到α>λ, 可得 从而有 于是有 证毕.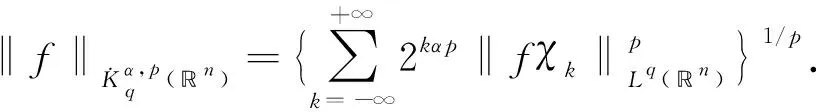
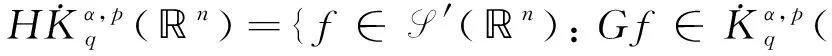
2 主要结果