基于密度信息熵的K-Means算法在客户细分中的应用

蒲晓川, 黄俊丽, 祁 宁, 宋长松

(1. 遵义师范学院 信息工程学院, 贵州 遵义 563006； 2. 国立釜庆大学 技术管理学院, 韩国 釜山 48513；3. 遵义师范学院 管理学院, 贵州 遵义 563006； 4. 河西学院 经济管理学院, 甘肃 张掖 734000)

在众多客户关系分析模型中, 最常用的是RFM模型(最近一次消费(Recency)、 消费频率(Frequency)和消费金额(Monetary)), 从多维度分析客户的价值. 在此基础上, 目前已有很多研究扩展了该模型的适用范围, 如文献[1]提出了一种以传统RFM模型为基础, 针对客户潜在价值的RFMP模型； 文献[2]在RFM模型的基础上构建了融入行业属性的RVS模型等. 但这些方法并未考虑客户的发展情况这一因素. 由于计算机数据挖掘中的聚类方法在应用上与企业客户关系管理相近, 因此可用聚类算法解决企业客户的管理问题.K-means聚类在算法时间度量指标及适用于大规模数据等方面效果较好, 因此广泛应用于解决客户细分问题中.

基于此, 本文提出一种基于客户发展的改进RFM模型, 并针对K-means聚类算法的初始聚类中心选取问题进行优化改进, 采用统计学方法和聚类效果对实验结果进行验证.

1 TFA模型构建

客户关系管理中的客户细分是指选择一定的细分变量, 按一定的划分标准对客户价值进行分类的方法[3]. 客户关系管理中最常用的是RFM分析模型, 但该模型存在细分后得到的客户群过多、 购买频率与购买金额之间存在多重共线性缺陷等[4]. 为克服RFM模型的缺点, 本文提出TFA模型, 是以客户发展空间T、 购买频次F和平均购买额A作为客户贡献度和发展空间的客户分类模型. TFA模型中,T表示客户发展空间,T值越大表示客户返店消费意愿越低,T值越小表示客户返店消费意愿越高, 其计算公式为

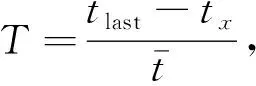
(1)

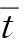
传统RFM模型未对其指标进行权重分析, 导致不能体现各指标在实际销售中的重要程度, 在改进模型中引入层次分析法(AHP)使之更精准. AHP是一种常用的权重分析方法[5], 首先将指标属性拆分为二维对应关系, 然后通过业内专家对属性进行权重判别. 本文通过填写专家问卷调查方法和层次分析法计算指标权重, 计算公式为

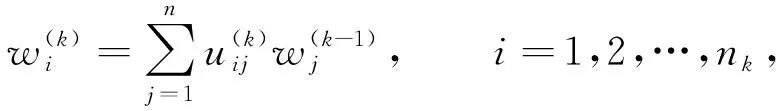
(2)

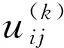
wTFA=0.26×T+0.11×F+0.63×A,

并通过

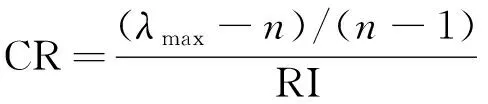
(3)

验证权重的一致性, 其中λmax为判断矩阵的最大特征根, RI为随机一致性指标. 若CR<0.1, 则说明权重系数在可接受范围内. TFA模型的指标含义及权重列于表1.

表1 TFA模型参数指标含义及权重

2 K-means聚类算法优化改进

由于RFM模型划分为8类, 在实际应用中存在划分过细的问题, 按照人为规则划分, 需要一种不设前提的细分方式, 并按照数据集规律进行分类, 随着数据挖掘技术的发展, 引入无监督的计算机算法已成为必然.

2.1 K-means算法

K-means算法的基本原理是将样本集中的样本按欧氏距离判断其相似度, 并划分到不同簇中, 使其簇间相异度最大. 算法基本流程如下：

步骤1) 从输入的数据点集合中随机选择K个点作为聚类中心；

步骤2) 对数据集中的每个点x, 代入

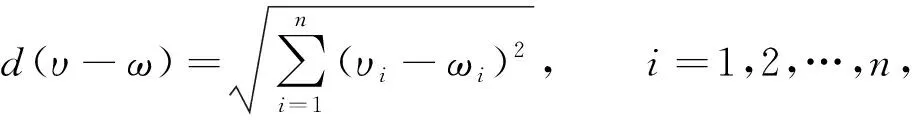
(4)

计算其与最近聚类中心(已选择的聚类中心)的距离d(x)；

步骤3) 将每个点按最近分配给每个聚类中心；

步骤4) 计算每个聚类群均值, 确定新聚类中心；

步骤5) 循环执行步骤2)～4), 如新聚类中心不再移动, 则终止计算; 否则转步骤2).

经典的K-means算法具有快速、 简单的优点, 有良好的可伸缩性, 处理大数据集效率较高, 其时间复杂度为O(nTK), 接近于线性, 适合挖掘大规模数据.但K值很难估计, 且初始点的选择会极大影响迭代次数及最终结果.

2.2 密度值及信息熵

参考文献[4]提出的密度计算方法.设数据集有n个样本数据X={x1,x2,…,xn}, 样本点xi的局部密度为ρi, 计算公式为

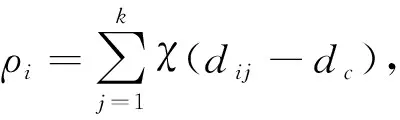
(5)

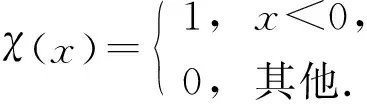
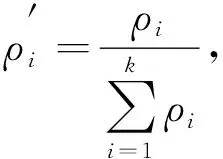
(6)

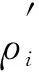
计算所有样本的密度概率, 并引入信息熵作为目标函数, 信息熵是对聚类混乱程度的度量, 如果信息熵较大, 则表明聚类混乱程度较大, 信息熵较小则混乱程度较小.因此, 数据集混乱程度表示为

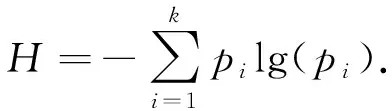
(7)

如果密度dc截距取值过大将导致局部密度概率值ρ′变小, 信息熵值过大, 则数据聚类不确定度过大; 如果dc过小将出现无法聚类的情形, 存在极值, 引入梯度下降法对信息熵进行求极值, 确定其极值点, 并将极值点所在的dc作为最佳截距.

2.3 改进K-means聚类算法

传统K-means聚类算法选取初始聚类中心时, 由于算法自身的敏感性和随机性, 易导致其聚类结果不稳定, 因此目前已提出了许多初始聚类中心选择改进方案: 如文献[6]提出了一种基于网格聚类与密度峰值的改进初始聚类中心选择算法; 文献[7]提出了一种基于数据空间网格化的簇中心选择算法. 本文受上述算法启发, 提出一种基于密度信息熵的初始聚类中心选取的改进算法, 算法流程如下.

算法1初始化聚类中心算法.

输入： 数据集阵列X,K值；

输出：K个初始聚类中心数据;

步骤1) 输入样本集X, 根据式(5)计算其密度值ρi；

步骤2) 根据式(6)计算局部密度概率ρ′, 并代入式(7)求出信息熵H的极值, 确定其最佳截距dc；

步骤3) 根据最佳截距排序并按密度值大小加入集合C中；

步骤4) 计算集合C中密度最大样本数据与集合中其他密度中心的距离, 取最大距离为第二中心点；

步骤5) 再选择与前两个点最短距离最大的点作为第三个初始聚类簇的中心点, 以此类推求出K个中心并进行聚类, 算法结束.

3 实验结果与分析

选择机器学习标准数据集和真实数据集作为实验对象, 选择K-means和基于密度的聚类(DBSCAN)算法进行对比测试. 采用Python编程环境, 集成约200个包, 采用Win10系统, 硬件环境为i7处理器, 16 GB内存. 真实数据来源为UCI机器学习存储库中Online Retail Ⅱ数据集, 共计约54万条数据, 描述某线上销售企业1年内的销售记录. 销售记录含订单号、 客户号、 商品描述、 订单金额、 生成订单日期等数据. 由于原始数据的质量会影响TFA模型细分的结果, 因此真实数据实验前需对原始数据进行预处理, 首先清洗缺失值并利用Pandas聚合函数及统计中的四分位方法对原始数据中的异常值进行过滤, 最后得到模型数据.

3.1 算法实验验证

选取UCI中4个较有特色的人工数据集(Iris, Wine, Digits, Glass)作为算法验证数据集. 将本文算法(Bwsf)实验结果与K-means和DBSCAN算法结果进行对比, 数据集属性列于表2.

表2 人工数据集属性

为有效统计并对比结果, 所有算法均在同一环境下运行50次, 取相应算法的最优值和平均值作为分析数据, 结果列于表3. 为更清晰地对比不同算法的差异, 图1和图2分别给出了不同算法的迭代次数和准确率对比. 由图1和图2可见, 本文算法在迭代次数上效果较好, 在聚类准确率上明显更稳定, 优于K-means和DBSCAN算法.

表3 不同算法的测试结果

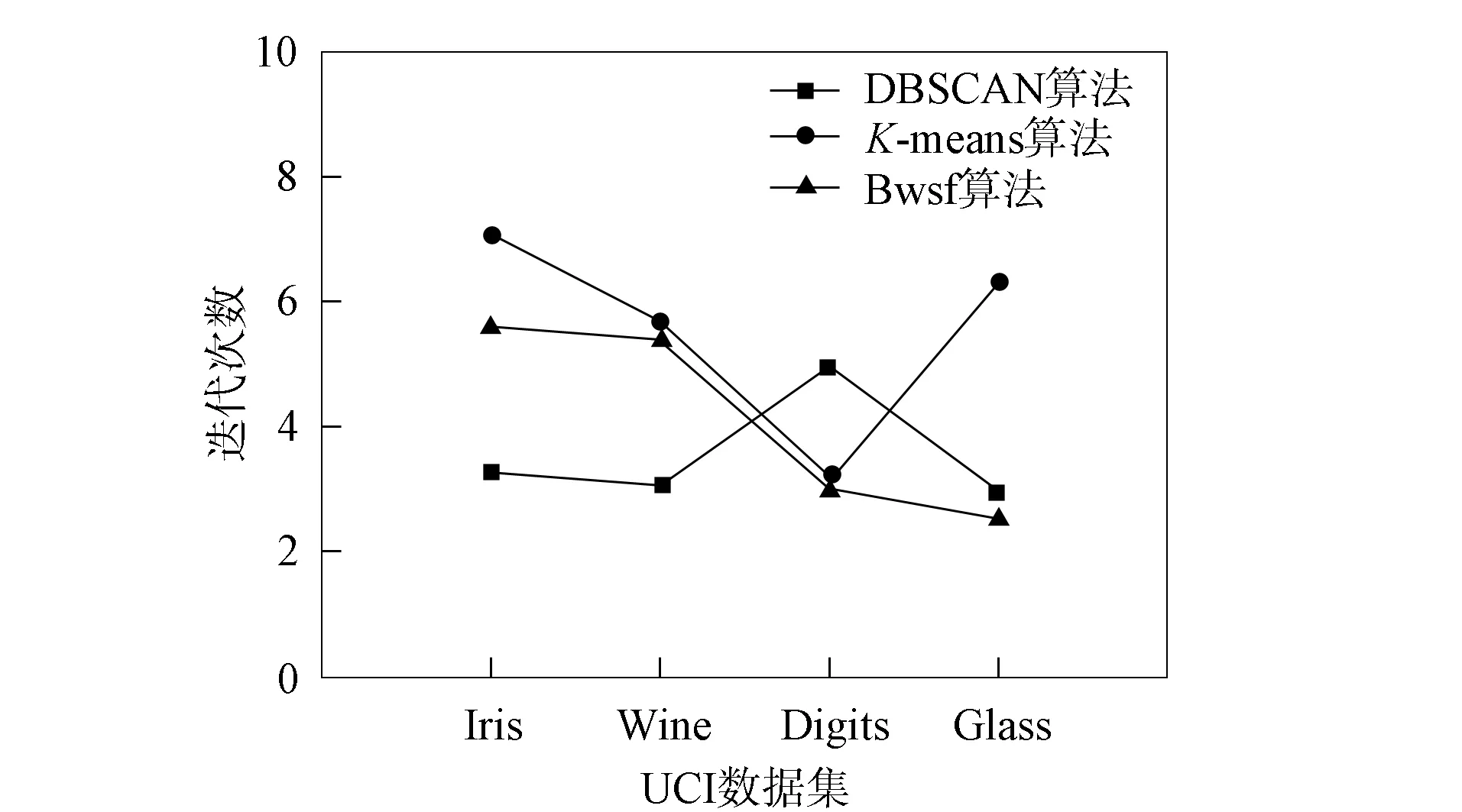
图1 不同算法的迭代次数对比Fig.1 Number of iterations comparison of different algorithms

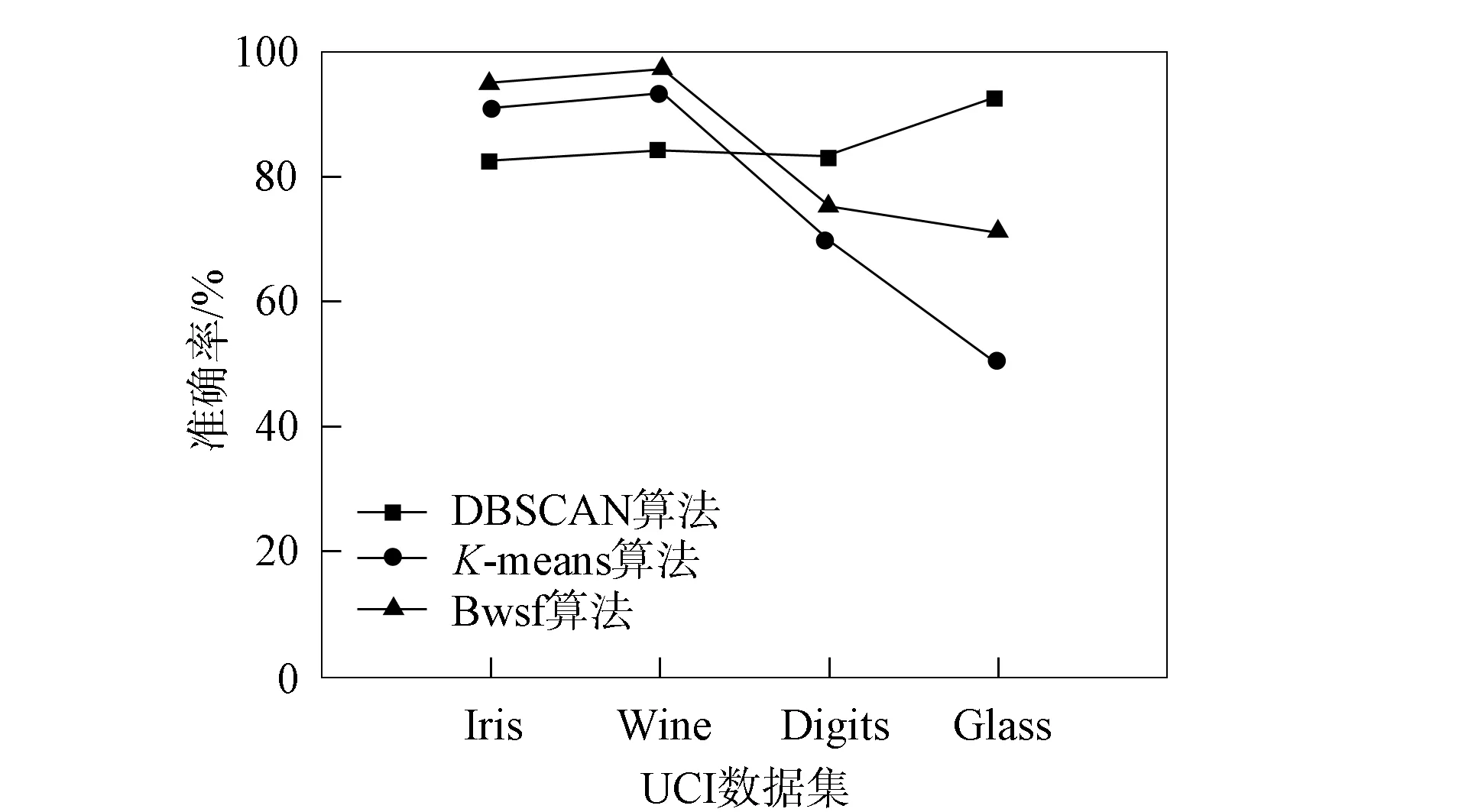
图2 不同算法的准确率对比Fig.2 Accuracy comparison of different algorithms

对降维后的人工数据集Iris,Wine,Digits及Glass使用本文算法同时进行可视化处理, 结果如图3所示. 由图3可见, 聚类结果基本符合算法测试数值.

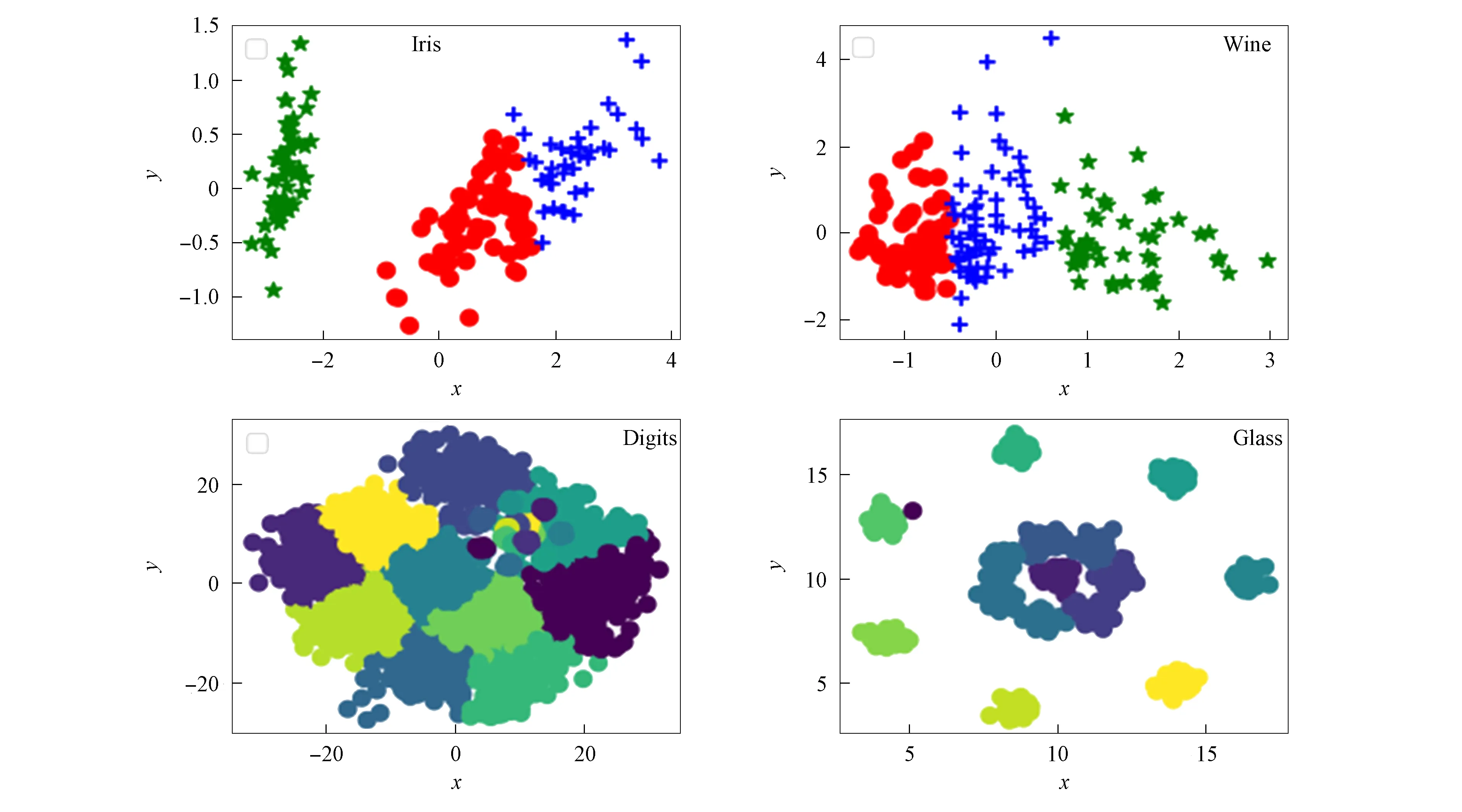
图3 本文算法对各数据集的聚类结果Fig.3 Clustering results of each data set by proposed algorithm

由上述算法验证结果可见, 改进K-means算法优化了聚类中心的选取, 并通过密度信息熵改善了原始算法易陷入局部最优、 对非簇数据集聚类效果较差的情形, 对比密度聚类算法没有数据的依赖性, 对于不同数据集有较强的兼容性, 并且适用于较大数据集的聚类.

3.2 真实数据集应用

真实数据集经过缺失值清理、 特征值、 四分位异常值清洗等处理后, 基于TFA模型, 从原始数据中生成模型指标, 需要对生成指标进行标准化处理. 常用方法有最小-最大标准化、Z-score标准化和均值归一化等. 本文采用Z-score标准化方法对生成指标进行处理. 利用Numpy.std函数将模型指标分别代入

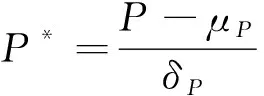
(8)

得到聚类算法的指标属性. 在K-means算法中, 为评估该改进聚类算法聚类效果和K值的合适度, 本文选择轮廓系数(silhouette coefficient)和Calinski-Harabasz指数对聚类结果进行评估, 轮廓系数计算公式为

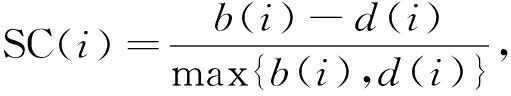
(9)

其中SC(i)∈[-1,1],b(i)表示第i个样本到同簇所有样本的平均距离,d(i)表示第i个样本到其他簇平均距离中的最小平均距离.b(i)也称为同簇的不相似度,d(i)也称为簇间的不相似度.SC(i)值越大, 聚类效果越好, 对应的K值为最佳聚类数.Calinski-Harabasz指数的计算公式为

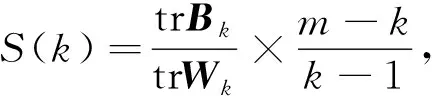
(10)

其中m为训练集样本数,k为聚类数, tr为矩阵的迹,Bk和Wk分别为簇间协方差矩阵和同簇内协方差矩阵.S(k)值越大聚类效果越好.

为验证TFA模型, 本文根据聚类结果数据计算了轮廓系数和Calinski-Harabasz指数, 并进行数据可视化对比, 结果如图4和图5所示. 为验证TFA模型聚类效果的有效性, 实验对比了RFM模型聚类与TFA模型聚类轮廓系数(SC)与Calinski-Harabasz(CH)指数的结果, 不同模型的聚类评估对比结果列于如表4. 由表4可见: 当K=6时, TFA模型在评估算法中SC值与CH值均最优； 而RFM模型在无监督聚类算法中, 聚类效果不佳, 如在轮廓系数中最佳聚类为K=2, 但在CH聚类评估中最佳聚类为K=8.

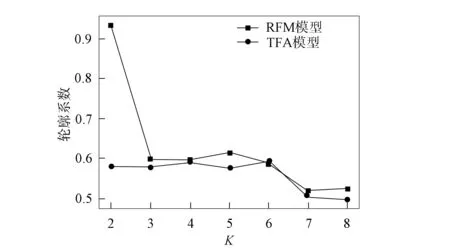
图4 轮廓系数对模型的评估结果Fig.4 Evaluation results of contour coefficients on model

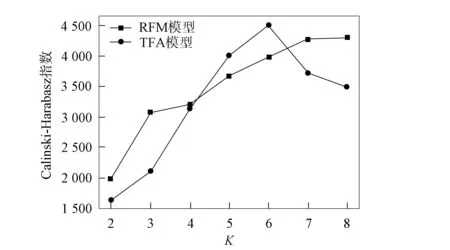
图5 Calinski-Harabasz指数对模型的评估结果Fig.5 Evaluation results of Calinski-Harabasz index on model

表4 验证算法结果

3.3 结果分析

无监督聚类结果一般从模型参数指标和聚类算法两方面考虑, TFA模型调整了指标参数, 更能有效体现用户分类的差异[8].

将TFA模型指标分别经改进K-means算法聚类后按聚类中心值汇总, 并将每类中心值按模型权重计算总价值, 结果列于表5, 表5中“↑”表示聚类效果提升, “↓”表示聚类效果下降, “_”表示聚类效果不变.

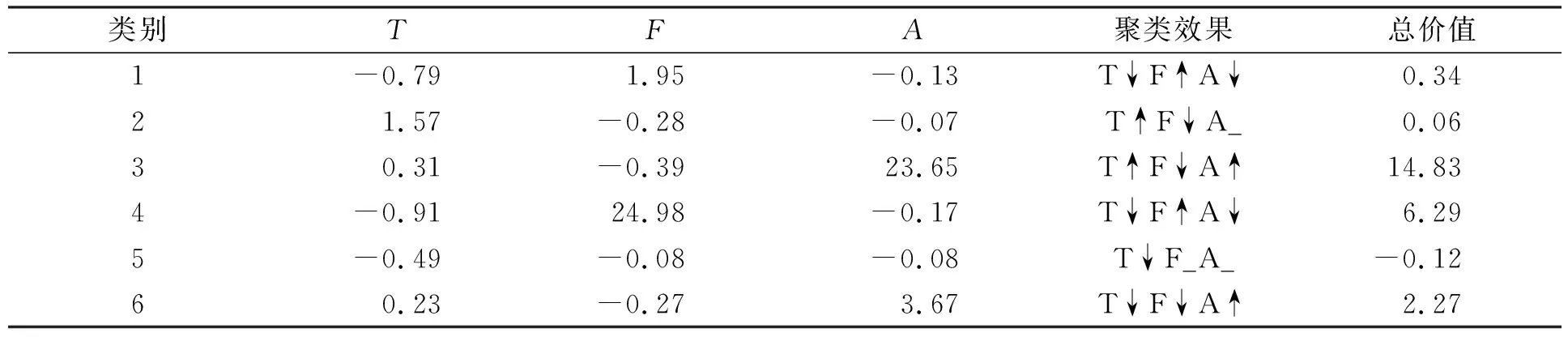
表5 TFA模型聚类分析结果

表6列出了TFA模型聚类客户级别对比结果. 由表6可见, 在该数据集中钻石型客户只有0.14%, 其在返店指标、 贡献度上均为最高, 但其消费频度为均值左右, 说明该类钻石型客户购买的产品均为高价值产品且利润较高; 高价值发展型客户, 在购买频次上最突出, 虽然其利润较低, 但其未来发展有很高的提升空间, 其价值仍然很高; 较高价值发展型为1.31%, 其表现为返店指标、 贡献度上较高, 消费频度较低, 从指标上判别有可能为新客户中购买能力较强者; 低价值发展型客户为5.86%, 其消费频次较高, 但因贡献度较低, 其价值也较低, 但从发展的角度需要对其关注； 高价值维护型用户所有指标都接近均值, 而且数量较多, 占比为23.77%, 该类客户为企业长期顾客, 相对稳定； 低价值易损型客户, 占比最大为68.83%, 这也是线上交易企业顾客流失率较高特点的体现.

从改进聚类算法性能分析, 由于本文算法数学模型较简单, 其复杂度较低, 因此易理解. 从其聚类评价分析, 如果TFA模型都选K=6的情形, 由表4可见, TFA模型指标使用本文算法比RFM模型使用本文算法有更好的聚类效果.

表6 TFA模型聚类客户级别对比结果

综上所述, 本文首先提出了一种基于客户发展空间的客户细分模型(TFA), 该模型使用客户发展空间、 购买频率、 平均购买额作为客户分类指标属性, 并加入了基于层次分析法的权重系数使其能体现指标属性的重要程度. 其次, 本文提出了改进的K-means算法, 通过引入密度信息熵初始中心选择算法, 有效避免了原始算法在初始中心选择上的不足. 最后, 通过人工数据集聚类准确率和迭代次数等指标及真实数据集聚类可视化分析进行实验, 实验结果表明, 该方法的分类结果有效且运行效率有所提升.