一种样本几何特征重构方法及其在迁移聚类中的应用

王 锦，尹汪宏

(安徽电子信息职业技术学院 信息与智能工程系，安徽 蚌埠 233030)

聚类作为最常用的无监督学习方法之一，已成功应用于许多场景，如文本分析、图像分割和临床决策支持[1-5]。聚类旨在将具有高相似性的对象分组到相同的簇中，将具有低相似性的对象分组到不同的簇中[6-8]。它可以将数据按照性质的相似程度进行归类。如此处理有利于后续的数据分析。但是在我们的现实生活中，数据采集往往会存在以下两种问题：(1)由于在生产中对数据有保密要求或者这是一个新兴产业，之前没有数据的积累，这就会导致采集到的数据量不足，无法满足传统的聚类分析所必备的基本条件；(2)在采集数据的过程中会遭到很多方面的影响导致丢失数据或者数据受到污染的问题，这样就会降低传统聚类分析算法的聚类性能。在这种情况下，一些传统的聚类算法就会失效。例如，MR图像被噪声污染或丢失像素后变得稀疏，一些经典的聚类算法FCM[9]，k-means[10]，AP[11]和DBSCAN[12]等不能直接应用或聚类效果很难达到标准。存在许多可用于处理这种情况的解决方案，其中迁移学习算法[11,13-17]受到更多关注。

在迁移聚类结构约束中，簇中心知识迁移是迁移学习最常用的准则，蒋亦樟等人[16]基于他们以往的研究GIFP-FCM提出了一种迁移聚类算法T-GIFP-FCM。CHEN A等人[13]在模糊聚类框架下提出了模糊迁移聚类算法PPKTFCM。HANG W等人[14]在Affinity Propagation (AP)[11]算法基础上，提出的迁移聚类算法TAP，该算法同样认为源域和目标域样本各簇中心尽量接近。TAP与T-GIFP-FCM和PPKTFCM不同，因为它不使用模糊聚类框架。尽管现有的聚类算法在迁移方案中表现良好，但是有些问题还是需要进一步解决。

(1)T-GIFP-FCM和PPKTFCM都来自FCM框架，因此它们的虚拟簇中心很容易受到噪声或离群点的影响。因此，当采用簇中心知识迁移进行迁移学习时，受噪声或离群点影响的源域中的虚拟中心可能对指导目标域的学习产生负面影响。

(2)虽然真实对象(样本或簇中心)被认为是TAP的中心，但有时只有单个簇中心代表簇的结构是不够的。

(3)用于目标域学习的迁移知识完全来自源域，使得目标域学习的性能严重依赖于源域的模式信息。

为此提出了一种基于簇内部结构重构(ICSR-T-FC)的迁移模糊聚类算法。首先，为每个簇中的每个对象分配权重以测量其对簇的代表性，使得每个簇的内部结构被每个对象所描述。其次，由于每个对象的权重由其邻近点赋予，可以将源域和目标域联合在一起以重建目标域中的簇内部结构。新簇结构的模式信息被认为是用于指导目标域学习的迁移知识。因此，迁移知识不仅依赖于源域，还依赖于目标域。

1 簇内部结构代表性表示方法

1.1 单代表点表示

其中比较经典的算法有FCM算法[18]和FCMdd算法[19]，但这两种算法又有区别。图1所示的是一个人工数据集以及FCM算法划分的结果。

图1 FCM算法在人工数据集上的聚类结果

从图1(a)中，可以看出，此人工数据集“+”所表示的簇相对于其它簇来说，样本数量较小，在利用FCM进行聚类时，由于类中心为虚拟中心，因此，对于较小的簇或离群点，容易出现“簇中心漂移”的现象，从而影响最终的划分结果，如图1(b)所示。

为了克服虚拟类中心所带来的问题，在模糊聚类理论的基础上，Raghu等人[19]提出了FCMdd聚类算法。相对于FCM而言，该算法选择数据集中真实的样本作为每个簇的簇中心，每个簇由一个代表点表示，则此算法称为“单代表点聚类算法”。

相对于虚拟中心，单代表点策略能够在一定程度上避免簇中心漂移问题，如在图2中，给出了FCMdd算法在图1(a)所示的人工数据集上的聚类结果，可以看出，FCMdd所获得的簇结构信息更接近真实情况。

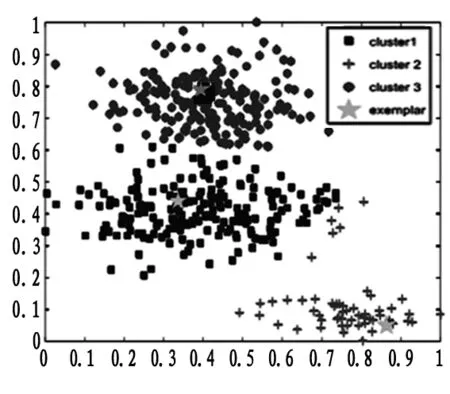
图2 FCMdd算法在人工数据集上的聚类结果

1.2 多代表点表示

大多数基于簇的聚类算法通常使用一个簇中心来表示簇结构，并期望对象被分配到最近的簇，并且不同簇之间的距离尽可能远。但是，在某些情况下，只有一个簇中心不足以表示簇。例如，图3表示了具有两个簇的数据集。从图3中可以看到簇1包含4个对象，其中任何一个都不足以表示其簇结构，因为其中没有任何一个可以被视为比其他更合适的对象。簇2包含6个对象，其中位于簇中心的两个对象几乎同时合理地被视为簇中心。换句话说，虽然选择其中一个作为簇中心可能不会严重扭曲簇结构，但可能无法发现所有候选簇中心的完整集合。

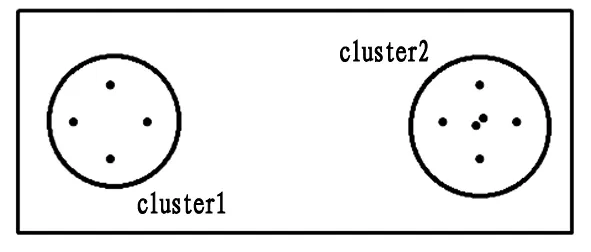
图3 簇内部结构代表性的示例

从上面的示例中，很容易发现多个样本簇的结构代表性比单个样本簇代表性具有更多优势。最近，已经有学者提出了一些关于基于多样本的聚类的研究。在文献[20]中，提出了一种多视图聚类算法，其中n个对象被用作表示簇的样本，其中n由用户预先设定。在文献[21]中，每个对象都被视为代表点。也就是说，簇内部结构由所有对象描述。他们的实验结果表明，所有对象赋予的这种代表性可以捕获足够的模式信息用于学习。

在本研究中，我们还使用这种代表性去通过为每个对象分配权重来捕获每个簇的内部结构，该权重表示着代表性的重要程度。

2 ICSR-T-FC:基于簇内部结构重构的迁移模糊聚类

首先给出所提算法的迁移机制，然后确立目标函数，并说明其详细的优化步骤。

2.1 知识迁移机制

通常而言，目标域和源域具有相似的对象分布特征。换句话说，应该最小化两个域之间的簇内部结构的差异。在该研究中，为了捕获足够的簇内部结构模式信息，为每个对象分配权重来表示相应的簇。此外，为了丰富用于目标域学习的迁移知识，还使用嵌入在目标域中的知识。迁移机制可以定义如式(1)。

(1)

其中，vcj表示目标域中簇c对象j的权重。K和N分别是目标域中的簇数和对象数。cj表示用于目标域聚类学习的迁移知识。如上所述，这里cj来自源域和目标域。在文献[21]中，从cj定义来看，可以知道cj的价值取决于它的邻近点。因此，为了重建目标域的簇结构并因此丰富迁移知识，可以将两个域联合在一起，然后更新目标域中涉及的每个对象的权重，并将新权重视为迁移知识cj。

2.2 目标函数和优化

利用式(1)中定义的迁移知识和多样本代表性策略，ICSR-T-FC的目标函数定义如式(2)、式(3)。

(2)

其中，uci表示属于簇c的对象i的模糊隶属度，rij表示对象i和对象j之间的相似性/不相似性。并且λ1和λ2是分别用于控制第一项和在迁移学习后项的权衡的两个参数。式(2)中的其他符号与式(1)中的符号相同。

很明显，ICSR-T-FC的目标函数包含三项。第一项计算簇内相似性/不相似性的总量应该最小化。第二项是二次项，uci可以视为“模糊隶属度”。λ1可以用来控制“模糊隶属度”的平滑程度。最后一项用于指导目标域的学习。它也是一个二次项，λ2被用来控制它的贡献程度。

从上面的形式可以看出，由迁移知识指导的目标域中对象的聚类问题可以表述为约束优化问题。由于模糊隶属度和每个对象的权重是连续变量，通过引入拉格朗日乘子和KKT条件[22]，可以得到拉格朗日目标函数L如下，

(4)

其中α1，βc，φci，Φcj是拉格朗日乘子，满足uci的KKT条件是

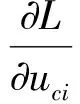
(5)

φci≥0

(6)

φciuci=0

(7)

在这里，请注意KKT成立的条件是保持uci≥0和vcj≥0。对于式(5)至式(7)，可以将uci更新的准则导出为

(8)

其中：

q-={c:μci=0}andq+={c:μci>0}

(9)

q+表示一组簇，其中对象i具有正模糊隶属度，q-表示对象不属于此簇的一组簇。并且|q+|和|q-|分别是q+和q-的大小。q+和q-可以通过以下程序确定程序Q

程序QStep 1:初始化q+(0)=ϕ,q-(0)=1,2,…,k,t=0;Step 2:t=t+1,q+(t)=q+(t-1)+{l},q-(t)=q-(t-1)-{l},其中l=argminc∈q-(t-1){∑Nj=1(vcj-vcj)rij};Step 3:校验,如果μfi>0,则根据式(8)计算μfi,f=argmaxc∈q+(t){∑Nj=1(vcj-vcj)rij}。如果成立,则返回步骤2,否则设置q+=q+(t-1),q-=q-(t-1),并终止。

同样，也可以获得相应的

(10)

其中：

p-={j:vcj=0}andp+={j:vcj>0}

(11)

在簇c中，所有涉及的对象被分成两个由p+和p-表示的集合。在p+中，所有对象具有正权重，在p-中，所有对象的权重均为零。并且|p+|和|p-|分别是p+和p-的大小。p+和p-可以通过以下程序确定程序P

程序PStep 1:初始化p+(0)=ϕ,p-(0)=1,2,…,N,t=0;Step 2:t=t+1,p+(t)=p+(t-1)+{l},p-(t)=p-(t-1)-{l},其中l=argminj∈p-(t-1){∑Ni=1μci-rij};Step 3:校验,如果vcg>0,则根据式(10)计算vcg,g=argmaxj∈p+(t){∑Ni=1μcidij}。如果成立,则返回步骤2,否则设置p+=p+(t-1),p-=p-(t-1),并终止。

2.3 ICSR-T-FC算法

算法1 ICSR-T-FC输入: 源域的相似矩阵D,目标域的相似矩阵D',簇数K,λ1,λ2和迭代停止阈值输出: 目标域的模糊隶属度矩阵U程序:1. 使用算法1.1获取迁移知识vcj;2. 规范化簇c中的迁移知识vcj;3. 随机化U;4. q=q+1;5. 根据U,利用式(10)更新权重矩阵V;6. 根据V,利用式(8)更新模糊隶属度矩阵U;7. 转至步骤4继续执行,直到|JICSR-T-FC(q)-JICSR-T-FC(q-1)|≤。

在算法1中，如下列出的算法2是用于获得迁移知识的子算法：

算法2 简化ICSR-T-FC输入: 源域的相似矩阵D,目标域的相似矩阵D',簇数K,λ1,λ2以及迭代停止阈值输出: 迁移知识vcj程序:1. 将每个对象的vcj设置为0;2. 随机化U;3. q=q+1;4. 根据U,利用式(10)更新权重矩阵V;5. 根据V,利用式(8)更新模糊隶属度矩阵U;6. 直到|JICSR-T-FC(q)-JICSR-T-FC(q-1)|≤;7. 转至步骤3继续执行,直到vcj=vcj。

3 实验结果

在本节中，将用不同类型的数据集评估ICSR-T-FC，包括合成数据集，UCI数据集和用于MRI分割的实际应用。此外，为了突出ICSR-T-FC的良好性能，介绍了几种类似算法，即FCM、AP、TAP和PPKTFCM。所有实验都在个人计算机上利用MATLAB软件实现，该计算机具有足够的运算能力。

3.1 评估标准

在实验中，引入了4个不同的标准用于评估。对于合成数据集和UCI数据集的聚类，引入归一化互信息(NMI)和调整随机索引(ARI)[23]来评价ICSR-T-FC和其他类似算法的聚类性能。假设有一个包含N个对象的数据集。用Nij来表示簇i和簇j之间共同的对象数量，其中簇i由算法生成，簇j是第j个真实簇。另外，分别使用Ni和Nj表示第i个簇和第j个簇中包含的对象的数量。因此，NMI和ARI可以定义为

(12)

(13)

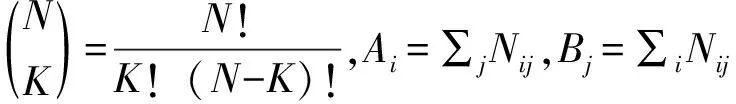
NMI的值从[0,1]获得，ARI的值从[-1,1]获得，值越大，聚类性能越好。

对于脑MRI分割，引入Dice系数(DC)和Jaccard相似度(JS)[5]用于聚类性能评估。假设Ai和Bi表示第i个真实聚类算法和生成第i个聚类的算法，DC和JS的定义如下，

(14)

(15)

其中|.|表示相应集的大小。DC和JS的值从[0,1]获得，值越大，聚类性能越好。

3.2 参数设置

关于ICSR-T-FC和引入的类似算法，表1给出了它们的参数设置。在表1中，对于每个参数，给出搜索间隔，通过结合NMI或ARI的网格搜索策略从间隔中搜索最佳参数。

表1 算法中主要参数的值或间隔

3.3 关于合成数据集

为了模拟迁移场景，可以使用高斯概率分布，利用平均向量[10 5]、[10 15]和[15-5]以及协方差矩阵[5 0；0 5]、[5 0；0 5]和[2 0；0 1]生成了包含90个对象的目标域和包含450个对象的源域。图4给出了目标域D-T和源域D-S的对象分布。

图4 合成数据集

对于目标域D-T中的对象，将它们分成2组或3组是合理的。如果D-T中的对象被划分为2个组，则标记为“+”的对象可被视为异常值或噪声。表2和图5给出了当簇的数量分别设置为2和3时的聚类结果。

这里，由于AP和TAP不需要预先设置K，因此当对象分别分为2个和3个簇时，以下给出了他们聚类的最佳结果。

从表2和图5可以看出，通过FCM获得的中心很容易被离群点或噪声干扰。当K设置为2时，请参见图5(a)中的聚类结果，可以说明FCM获得的每个簇的中心都是虚拟的。尽管AP使用样本中的实际对象作为其簇中心，但在某些情况下，一个对象不足以描述簇内部结构，当K设置为3时，请参见图5(b)中的聚类结果。与FCM和AP进行比较，ICSR-T-FC不仅使用真实对象作为簇中心，而且还使用多样本代表性策略，使得获得的簇中心对于离群点或噪声更具有鲁棒性，并且可以充分捕获簇内部结构，参见图5(c)中的聚类结果。

表2 D-T聚类结果

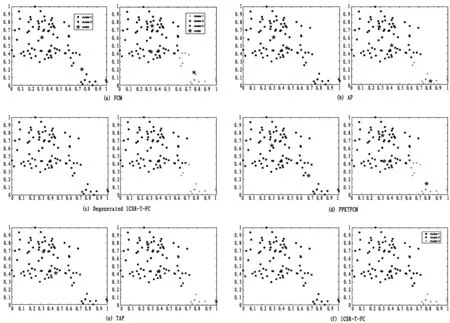
图5 合成数据集的聚类结果

此外，与引入的迁移聚类算法TAP和PPKTFCM相比，ICSR-T-FC也实现了最佳性能。特别是当K设置为3时，ICSR-T-FC的NMI和ARI表现很完美。由于对象稀疏地分布在目标域D-T中，因此簇内部结构信息变得难以捕获。虽然可以根据源域提供的簇中心知识迁移来使用迁移知识来指导目标域的聚类过程，但仍然不足以有效地处理稀疏分布问题。在ICSR-T-FC中，将两个域联合在一起，重建目标域的簇内部结构，并以新结构作为迁移知识来指导目标域的聚类过程。实验结果也证明了该策略的有效性。

为了进一步评估ICSR-T-FC的性能，将在实际迁移方案中实施该算法。

3.4 关于UCI数据集

选择20个集合中的4个集合来生成两个称为“comp VS sci”和“rec VS talk”的迁移场景。表3给出了有关这两种迁移场景的详细信息。

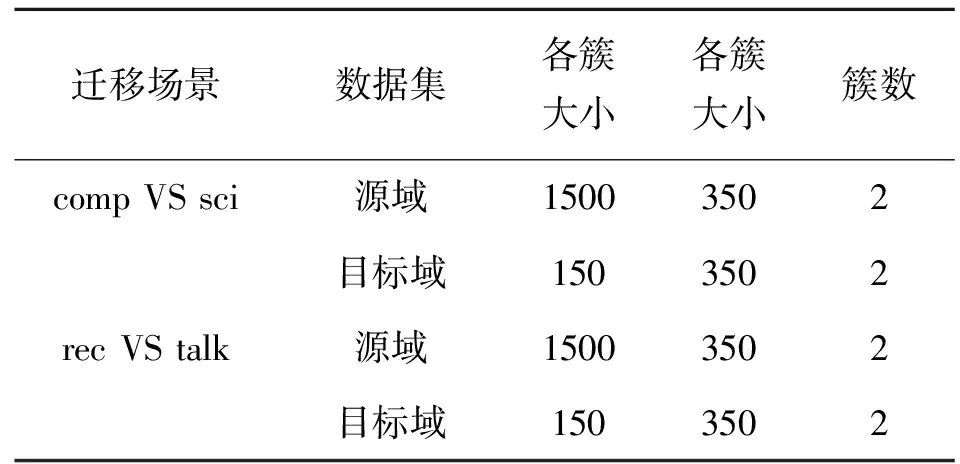
表3 两种迁移场景的描述 簇

表4展现的是所有算法在NMI和ARI方面的聚类结果。从表4中，可以看到ICSR-T-FC在所有类似算法中也获得了最佳性能，这与合成数据集的结果一致。

表4 在UCI数据集上的聚类结果

实验结果表明，将两个域联合在一起，重建目标域的簇内部结构，并以新结构作为迁移知识来指导目标域的聚类过程能够起到知识迁移的作用，对目标域而言，能够提升目标域的聚类效果。

4 结论

本研究提出了一种基于簇内部结构重构的迁移模糊聚类算法，并使用所有对象信息来描述簇内部结构。将目标域和源域联合在一起以重建目标域的簇结构，并重新计算目标域中每个对象的权重。目标域中更新后的权重被认为是用于指导目标域学习的迁移知识，利用新的簇结构作为迁移知识来指导目标域中簇的划分。不同类型数据集的广泛实验结果表明，与其他迁移聚类算法相比，所提出的迁移模糊聚类算法具有更好的性能，表现出更好的聚类效果。