贝叶斯公式的微课教学设计与实践

王 燕

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

作为解决复杂概率问题的一个重要工具，贝叶斯公式是概率论教学中的重点和难点，同时又是贝叶斯统计的理论核心，以此为基础发展起来的贝叶斯估计、贝叶斯网络、贝叶斯分析、贝叶斯学习等理论在人工智能、数据挖掘、经济预测、医学诊断、质量监控等领域发挥着重要的作用，因此，学习和理解贝叶斯公式非常重要。

1 贝叶斯公式教学设计的思路

从学生熟悉的小故事、生活中遇到的实际问题和概率中经常列举的质量检测问题引申出教学内容，调动学生的学习兴趣，激发学生的求知欲。通过引例，引导学生利用条件概率公式和全概率公式，推导出贝叶斯公式的具体形式及求解方法。在给出贝叶斯公式之后，对公式的条件、应用背景进行深入的解读，让学生更加深入地理解贝叶斯公式，并简单介绍一下贝叶斯的生平，让同学们认识到任何一个数学公式或者理论的产生都不是那么容易的。给出贝叶斯公式在信用问题中应用的例子，此案例既与学生所学专业背景有关，又能很好地体现课程思政，在讲解例子的过程中，给同学们解释了先验概率和后验概率，这是本节的难点，但基于实例对于两个概念的理解是十分有利的。最后，进一步列举贝叶斯公式的其他应用领域，扩展本节学习内容。课后思考题的选择，是贝叶斯公式在“疾病诊断”中应用的案例，这个案例既有益于学生理解先验概率和后验概率，也能增强学生解决实际问题的能力。

2 贝叶斯公式教学过程的设计

2.1 创设情景，图片案例引入

从“狼来了”的故事中村民们对小男孩的信任度如何急剧下降，体检中某项指标出现异常时医生让患者复查的依据，产品出现质量问题时如何追究经济责任等问题，一步步设问，引出微课教学内容——贝叶斯公式。

为了推导出贝叶斯公式，给出一个产品检验中的例子。引例与最开始提出的问题相契合，背景简单，易于理解。

例1某工厂有三条生产线生产同一种产品，设三条生产线线的产量分别占总产量的0.25、0.35、0.40，又设这三条生产线的不合格品率依次为0.02、0.02、0.01。若该厂规定，出了不合格样品要追究有关生产线的经济责任，但该商品是哪一条生产线生产的标志已经脱落，问每条生产线应该承担多大的责任？[1]

分析首先设出随机事件，设A为抽取的产品为不合格品，B1,B2,B3分别表示抽取的产品是第i(i=1,2,3)条生产线生产的，则B1,B2,B3为样本空间S的一个划分，由题意可知三条生产线生产的概率分别为P(B1)=0.25,P(B2)=0.35,P(B3)=0.40，抽取的产品是第i(i=1,2,3)条生产线生产的，它正好是不合格品的概率分别是P(A|B1)=0.02,P(A|B2)=0.02,P(A|B3)=0.01，这些都是条件概率。

要追究三条生产线的经济责任，即为计算这件不合格品正好属于第i条生产线的概率，也就是考查P(Bi|A)(i=1,2,3)的值。

代入数据，可以求得

分析一下这些数据的意义，以P(B1|A)=0.3125为例，它表示如果这件产品是不合格品，它是第一条流水线生产的概率是31.25%，也就是第一条流水线要承担的31.258%的责任。假设罚款100元，第一条流水线要罚31.25元。

通过比较可以看出，不合格品来自第三条流水线的可能性是最大的，因此，第三条流水线应该承担最大的责任。

结论由条件概率的定义、乘法公式、全概率公式推导得到的这个公式实际上就是贝叶斯公式，把它一般化，就可以得到贝叶斯公式的精确表述。

2.2 贝叶斯公式

定理[2]设试验E的样本空间为S。A为E的事件，B1,B2,…,Bn为S的一个划分，且P(A)>0,P(Bi)>0(i=1,…,n)，则

称为贝叶斯公式。

解读公式

1.对公式条件的条件进行解读，B1,B2,…,Bn为S的一个划分，保证了分母可以按全概率公式展开，P(A)>0,P(Bi)>0是为了保证公式中的两个条件概率有意义。

2.公式中的A看成是结果，B1,B2,…,Bn看成是导致A发生的所有可能的原因，是一个“已知结果求原因”的公式。由于全概率公式是“知因求果”正向思维，而贝叶斯公式是“执果索因”逆向思维，也被称为“逆概率公式”。

3.贝叶斯公式的历史：最早是英国的数学家贝叶斯提出来的，所以以他的名字命名。他所发表的有关贝叶斯公式的文章很长一段时间内在学术界都没有引起什么反响，可时至今日，贝叶斯公式已经发展成一整套统计推断方法——贝叶斯统计，应用非常广泛。

2.3 应用——信用问题[3]

例2某商业银行对创业人群提供小额贷款，某人承诺两年内还清贷款，否则视为不守承诺。假设对该人的信任度为0.7，可信的人不遵守承诺的概率为0.1，不可信的人不遵守承诺的概率为0.8。若此人两年内未还清贷款，求银行对此人的信任度为多少？

解读名词信任度，就是指可以被相信的程度，是一个人是可信的人的概率的大小。

分析这个人两年内未还清贷款，即为一个不遵守承诺的人，可信的人可能会不遵守承诺，不可信的人也可能会不遵守承诺，所以这个人可信与否构成了不遵守承诺的所有可能原因，很明显，这两个原因是互斥的。如果把创业人群看成是一个样本空间，那他们就是样本空间的一个划分，问题是若此人两年内未还清贷款，求银行对此人的信任度为多少？也就是求：若这个人未遵守承诺，他是一个可信的人的概率是多少？这是一个“已知结果求原因”的问题，可以应用贝叶斯公式解答。

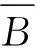
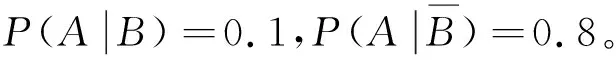
由贝叶斯公式得，

结论若这个人未及时还清贷款，他的信任度将由0.7降至0.23，其信用程度大大降低。

延伸1贝叶斯公式的一个重要应用，就是在新信息的条件下，对B事件概率的重新估计。一般来说，贝叶斯公式中，A事件未发生前Bi事件的概率定义为先验概率，有了A事件这个新信息后，再对Bi事件发生的概率的估计定义为后验概率，贝叶斯公式正是在计算这个后验概率。这道题目中，P(B)为先验概率，P(B|A)为后验概率。

延伸2进一步思考下面的问题：如果此人之后再次提出贷款申请，承诺两年内还清贷款，银行批准。若此人两年内又未还清贷款，求银行对此人的信任程度变为多少？

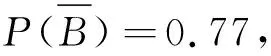
这个人第二次未及时还清贷款后，其信任度已经下降到0.036，从0.7到0.23，再到0.036，贝叶斯公式从数量上体现了这个人的信任度是如何急剧下降的。

如此低的信任度，将给个人的征信带来污点，以后这个人的房贷、车贷、信用卡等都会受到影响。贷款额度要比别人的少，利率要比别人的高。如果逾期严重，甚至坐飞机、高铁，住宾馆都无法透支消费，子女无法上重点学校，失信寸步难行。

延伸3贝叶斯公式的应用远不止此，在疾病诊断、经济预测、刑侦决策和质量控制等凡是用到概率预测的地方，都会用到贝叶斯公式，贝叶斯公式无处不在。

2.4 小结

1.贝叶斯公式是一个平凡的公式，它是由条件概率、乘法公式和全概率公式推导得出的；

2.贝叶斯公式又是一个神奇的公式：它是逆概率公式，实现了P(A|Bi)到P(Bi|A)的转化；它是一个由果求因的公式，与全概率公式正好相反；它本质上体现了利用样本信息对先验概率的修正。

2.5 思考题

思考题某一地区肝癌的发病率为0.0004，先用甲胎蛋白法进行普查。医学研究表明，化验结果是存在错误的。已知患有肝癌的人其化验结果99%呈阳性(有病)，而没有患肝癌的人其化验结果99.9%呈阴性(无病)。现某人的检验结果呈阳性，问他真患肝癌的概率是多少?

延伸思考

1.检验结果呈阳性是否一定患有肝癌？

2.这种普查对于诊断一个人是否患有肝癌有无意义？

3 教学总结

关于贝叶斯公式的微课设计，主要有以下几个特点：

(1)步步紧扣，教学设计体现完整性与逻辑性。各个教学环节和内容的设计衔接紧密，逻辑性强，体现了设计的完整性与合理性，前面的案例与后面的例题讲解形成了首尾呼应的良好效果。

(2)遵循规律，教学过程注重数学思想方法的渗透。教学过程中通过一步步的设问引出今天的教学内容，主体按照“由引例引出贝叶斯公式—贝叶斯公式的精确表述—回到贝叶斯公式的应用”的顺序组织教学内容，使学生能全面认识所学内容，形成完整的知识框架，还能培养学生应用数学解决实际问题的意识。

(3)合理选择，开发案例教学中的思想政治元素。诚信是社会主义核心价值观的重要组成部分，是做人做事的基本准则。通过讲解贝叶斯公式在信用问题中的应用的例子，建立了诚信模型，教育学生做人做事要讲诚信[4-6]。