师范认证背景下实变函数习题课的教学探讨——以集合可测的条件探讨及其应用为例

王 文，周 辉，余 静

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

培养学生的数学核心素养不仅是中学课堂的重要目标，也是大学课堂的重要目标。针对师范生课堂教学来说，培养学生的数学核心素养也是教育部对师范专业师范认证的重要指标之一。如何培养学生用数学的眼光观察问题、用数学的思维分析问题、用数学的思想解决问题是课程改革理念的一项重要任务，也是师范生教学能力培养的重要目标之一。而问题是数学的灵魂，如何培养学生提出问题、分析问题、解决问题的能力，从问题的特殊情形抽象出一般结论的能力是大学数学教学关键点，也是落脚点。

在实变函数教学中，测度就是长度概念的一个推广，在实数集R中能够量出长度的点集是很少的，因此，需要把长度的适用范围扩大，使更多的集合具有一定意义的长度，也就是所谓的测度。类比长度公理，数学家Lebesgue提出了测度公理[1]，就是保留了长度公理中的非负性和正则性，将其中的有限可加性推广到可数可加性。

那么如何找出具有这些性质的测度m以及关于m的可测集类呢？首先引进外测度，外测度对R中的任意点集都有定义，满足非负性和正则性，但不一定满足可数可加性。然后，对外测度的定义域加以约束，即在R中找某一集合类μ，使得外测度在μ上满足可数可加性。此时，μ中的元素就称为可测集，可测集的外测度也就是它的测度了。

本文主要探究如何引导学生自主探寻可测集的判定条件。

1 可测集的判断条件

从可测集的定义出发，有目的地引导学生探寻集合可测的判定条件，是探寻实变函数教学改革的目标之一，更是师范类院校培养师范生教学技能、引导学生深挖教材的重要手段之一。下面以总结归类的方式进行启发式探讨。

目标： 探讨集合可测的判定条件以及充要条件。

设计思路一从简单的可测集类出发，先引导学生给出简单集合可测的判定条件，并简单给出理由，比如外测度为零的集合。

结论1外测度为零的集合可测。

证明∀T⊂Rn，有m*T≤m*(T∩E)+m*(T∩Ec)≤m*(E)+m*(T)≤m*(T)

从而m*T=m*(T∩E)+m*(T∩Ec)，即E为可测集。

设计思路二引导学生通过类比数学分析中求极限的方法之一：两边夹定理，那么判断集合可测是否有类似的方法呢？

探索过程 类似求极限的两边夹定理，需要找到两个合适的可测集，使得点集E包含在中间，而且两端可测集的测度要相等。在不断的分组探讨中，学生在利用外测度单调性的推理过程中发现，可以将两端的可测集修改为两个可测集列，即存在两列可测集{Fn},{Gn},使得Fn⊆E⊆Gn且m(Gn-Fn)→0(n→∞)，可得到点集E的可测性。如是最终探究出所要的结论，如下：

结论2设E⊆Rm，存在两列可测集{Fn},{Gn},使得Fn⊆E⊆Gn且m(Gn-Fn)→0(n→∞)，则E可测。

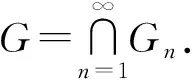
(G-E)⊆(Gn-E)⊆(Gn-Fn)，

由单调性得0≤m*(GE)≤m*(Gn-E)≤m*(Gn-Fn)=m(Gn-Fn)→0(n→∞)，

因此，m*(G-E)=0，则G-E可测，故E=G-(G-E)可测。

设计思路三引导学生通过类比数学分析探寻函数可积时，证明上和的下确界与下和的上确界相等，那么判断集合可测是否有类似的方法呢？

与探索过程 (1)类似求曲边梯形面积的内填外包法，需要构造能够覆盖点集E的可测集测度的下确界，以及包含点集E的可测集测度的上确界；(2)根据开集和闭集是可测集，以及Rm中有界闭集和紧集的等价性，构造inf{mG:G是开集，E⊆G}和sup{mH:H是紧集，H⊆E}；(3)假设两者相等，尝试能否得到点集E的可测性？最终探究出所要的结论，如下：

结论3若有界集E⊆Rm满足条件：

inf{mG:G是开集，E⊆G}=sup{mH:H是紧集，H⊆E}，则E是可测集。

证明记inf{mG:G是开集，E⊆G}=sup{mH:H是紧集，H⊆E}=c，由上下确界的定义，对任意的自然数n，存在开集Gn，紧集Hn，使得Hn⊆E⊆Gn,且

即存在可测集列{Hn},{Gn},使得Hn⊆E⊆Gn，且

由结论2可得E可测。

此外，还有同学直接通过开集和闭集的可测性，也能直接利用开集或闭集直接来刻画可测集，得到下面充要条件：

结论4设E⊆Rm，E是可测集⟺对任意ε>0，存在开集G，使得G⊇E且m*(G-E)<ε。

结论5设E⊆Rm，E是可测集⟺对任意ε>0，存在闭集F，使得F⊆E且m*(E-F)<ε。

2 解题中的应用

通过总结归类的方式进行启发式探讨，让学生自主总结判断集合可测的一些判定条件，老师紧接着给出几道练习题，让大家合理应用判定条件来解题，最终让学生真正领悟并掌握这些重要的结论。

例1设A1,A2⊆Rn,A1⊆A2，A1是可测集且有m(A1)=m*(A2)<∞，试证明A2是可测集。

证明由于A1是可测集，根据Caratheodory条件，取T=A2，则

由于m(A1)=m*(A2)<∞，因此m*(A2-A1)=0。则由结论1知A2-A1可测。所以，A2=(A2-A1)∪A1是可测集。

例2设E⊆Rm，对任意ε>0，存在开集G1,G2，使得E⊂G1,Ec⊂G2,m(G1∩G2)<ε，则E是可测集。

证明对任意n∈，存在开集An,Bn，使得

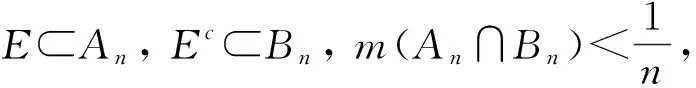
由结论2得E可测。

注本题的解答合理运用了判定条件2，事实上，此题反过来也是成立的，也就是说，这也是一个充要条件。

3 结语

在本节课的教学中，充分调动了学生的积极性，使他们在老师的适当引导下积极参与探索，也成功融入了翻转课堂的教学理念，让学生成为课堂的主体，在整个过程中，也体现着数学核心素养。通过问题驱动，培养学生对数学的热爱，让学生体验数学之美，激发他们的求知欲，也可以增强学生提出问题的意识，提升数学抽象、批判性思维的能力。