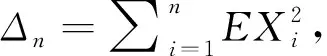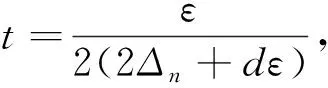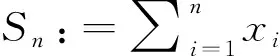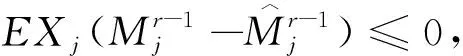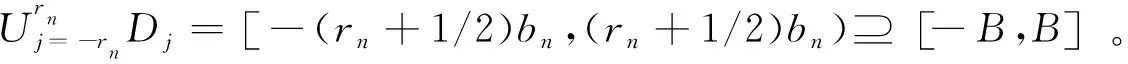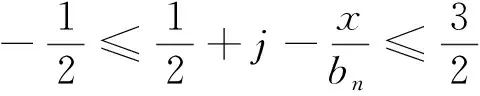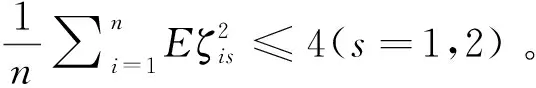拓广负相依样本下频率插值估计的一致强相合性
邢国东,康晴晴
(合肥师范学院 数学与统计学院,安徽 合肥 230601)
1 综述
首先,回顾一下拓广负相依随机变量的概念,此概念是由Liu[1]给出的一有限随机变量集{Xi,1≤i≤n}被称为拓广负相依的(简记为END)如果对于所有的实数X1,…Xn,存在一常数M>0使得
和
都成立,一无限集{Xi,i≥1}是END如果它的任何有限子集是END。
已知的事实是独立随机变量和负限相依的(简记为NOD)随机变量是END。Joag-Dev和Proschan[2]指出负相协的(简记为NA)是NOD,但NOD不一定是NA,故而NA随机变量是END。接下来,简要地介绍频率插值估计。设X是一个密度函数为f(x)的连续随机变量并令X1,…Xn是从总体X中抽取的一组样本。考虑一实数轴的等距离分割… (1) 正如Scott[3]所指出的那样,频率插值估计与核密度估计有着相似的收敛速度但比直方图估计的收敛速度快。频率插值估计的计算效果和直方图的相等。此外,对于大量的二元数据集合,频率插值估计计算的简单性和决定确切等概率轮廓精度的便捷性使得频率插值估计比具有高精度的核密度估计更有价值。因为频率插值估计的这两方面优点,对其做进一步的研究是有意义的。 近十几年来,有关频率插值估计的一些结果已经被得到。例如,Carbon等[4]在α混合过程下给出频率插值估计的最优窗宽(此时的窗宽使得积分均方误差达到渐近最小值),渐近方差,强相合性及其收敛速度。Carbon等[5]得到随机域下频率插值估计的渐近正态性。Besaid和Dabo-Niang[6]在连续随机域下给出频率插值估计的积分均方误差以及强相合的收敛速度。受到上述作者的启发,将在END样本下通过一Berstein型指数不等式探讨频率插值估计的强相合性。此外,相应的收敛速度也被给出。 在本文中,总假定C代表了一个正常数,此数仅仅由某些给定的数而定且从文中的一处到另一处可能会不一样,窗宽和密度函数分别被表示为bn和f(x),g(n)=max{gL(n),gU(n)},只要没有作特殊说明,所给出的极限都是在n→∞时得到的。本文的结构如下:第二部分包含了所得到的主要结果,对应的证明被放在本文的第三部分。 为了方便表述主要结果,需要下面的一些假设: (A1)假设Xi,{1≤i≤n}是一END样本,其密度函数为f(x)。 (A2)bn→0。 根据上述假设,可以给出如下所示的主要结果。 定理2.1如果假设(A1)~(A3)成立,那么对于的紧子集D, (2) 此外, 如f(x)对于x∈是可微的且对于某个M>0有|f(x)′|≤M, 那么 (3) 于是 (4) 推论2.1如果假设(A1)-(A2)成立,f(x)对于x∈是可微的且对于某个M>0有|f′(x)≤M|那么 (5) 在这一部分,将给出主要定理的相关证明。为此,需要如下引理。 引理3.1令X1,…,Xn是END。如果函数g1,…,gn都是非降的或非增的,那么随机变量g1(X1),…,gn(Xn)也是END[1]。 引理3.2令{Xi,1≤i≤n}是一均值为零且|Xi|≤da.s.的END随机变量序列,其中d是一正常数[7]。设t>0使得对于n≥1有t·max1≤i≤ndi≤1,则对于任意ε>0,存在一常数M>0使得 (6) 其中M>0。 Mj=max{0,Xj+1,Xj+1+Xj+2,…Xj+1+Xj+2+…Xn} 和 那么当1 上述给出的极大矩不等式可用于统计学中加权估计渐近性质的研究,这类估计包括最小二乘估计,非参数回归估计以及非参数密度估计等。 基于引理3.1和3.3,可以给出定理2.1的证明,具体过程如下所述: (7) P(|fj-Efj|>ετn/3)+P(|fj+1-Efj+1|>ετn/3)。 (8) 对于一给定的j,令 ζi=I{(j-1)bn≤Xi I{Xi≥(j-1)bn}-EI{Xi≥(j-1)bn}-{I{Xi≥jbn}-EI{Xi≥jbn}}=:ζi1-ζi2i=1,2…,n。 (9) 将上述结果和bn→0,τn→0以及n(bnτn)2(logn)-1→∞联合在一起,则对于任意给定的q>0和充分大的n可得 P(|fj-Efj|>ετn/3)≤Cexp{-qlogn}≤Cn-q。 (10) 类似地,也有 P(|fj+1-Efj+1|>ετn/3)≤Cexp{-qlogn}≤Cn-q。 (11) 联立(3.3),(3.5)和(3.6)可得 (12) 通过在(3.7)中取q=3,(3.2)以及nbn→∞,得到 (13) 上式意味着在给定的条件下(2.1)是成立的。此外,再应用泰勒展开式,可得(2.2),证毕。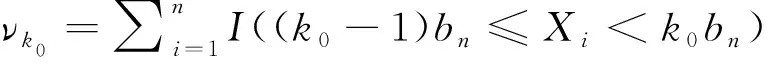
2 主要结果
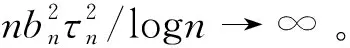
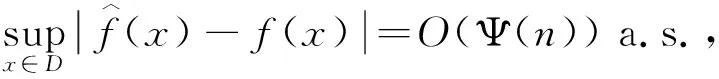
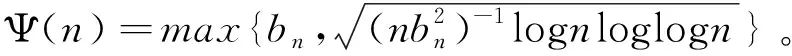
3 证明