矩形钢管加厚对容许长细比的影响研究

张 杨，龙珊珊，张 满

（1.黄冈职业技术学院 建筑学院，湖北 黄冈 438002； 2.湖北精诚钢结构股份有限公司，湖北 黄冈 438002； 3.湖北天工建筑勘察设计有限公司 罗田分公司，湖北 罗田 438002）

钢结构工程施工过程中，经常会遇到原材料规格短缺而出现的钢材代换问题。大多数情况下，用较厚的钢板代替较薄的钢板都能满足结构受力和构造要求，但对于某些构件，若不经验算直接增加厚度，可能会使其惯性半径减小、长细比增大，甚至不能满足现行规范对于容许长细比的要求。

著名的魁北克大桥垮塌事件证明了容许长细比的重要性，忽视容许长细比会给对工程造成毁灭性的质量事故。厚壁矩形钢管细长杆由于自重较大、惯性矩相对较小，加工、运输、起吊以及安装后处于横放状态都会累加其弯曲变形，导致具有初始弯曲变形的细长杆在压力作用下产生二阶弯矩，细长杆在二阶弯矩的作用下，弯曲变形进一步加大，截面边缘的钢材极易进入屈服阶段，从而对整体结构造成了较大的安全隐患。笔者试图分别从理论、试验和实践角度，分析加厚矩形钢管外壁对容许长细比的影响，以及其对整体结构安全性的影响，供同行探讨。

1 长细比的概念及计算方法

在建筑结构设计中，长细比是指杆件的计算长度与杆件截面的惯性半径（也称回转半径）之比，一般情况下长细比越大，杆件的整体稳定性越差，反之其稳定性越好。我国《混凝土结构设计规范》《钢结构设计标准》等现行规范指出：杆件的稳定系数随着长细比的增大而减小，杆件的承载力随着稳定系数的增大而增大，即杆件的承载力随着长细比的增大而减小。这种算法在美国、英国结构设计规范中也广泛采用，其计算结果与实际情况的吻合度较高。

根据我国《钢结构设计标准》，轴心受压构件长细比的计算方法如下：

长细比的要求如下：

由我国现行规范可以看出，长细比不仅对杆件的承载力有直接的影响，而且在杆件的制作、运输、安装、受力过程中控制变形，也起到一定的参考作用。我国《钢结构设计标准》规定的轴心受压构件的容许长细比在120~200之间，轴心受拉构件的容许长细比在200~400之间，美国LRFD钢结构规范规定的轴心受压杆的容许长细比为200，轴心受拉杆的容许长细比为300，比我国更加宽松。经过我国近年来的工程实践证明，我国容许长细比取值是可靠的，绝大部分构件在制作、运输、安装、受力等阶段中没有发生过大的变形，使用过程中发生重大损坏的情况也比较少。反观美国，在诸如奥尔良飓风等一系列自然灾害面前，很多轻钢结构房屋发生了毁灭性的损坏。

2 矩形钢管加厚对细长比的影响问题

在工程设计实践中，笔者发现较多工程人员对容许长细比的重视程度不足，随意甚至强行加大矩形钢管的壁厚，导致部分工程存在一定的安全隐患，因此有必要专门针对矩形钢管加厚对容许长细比的影响进行分析和研究。

与H形截面等开口截面不同，闭口截面的厚度越大，其惯性矩反而越小。按照长细比的计算方法，相同外直径的钢管，其壁厚越薄，惯性半径越大，部分矩形钢管截面的惯性半径及承载力统计见表1。

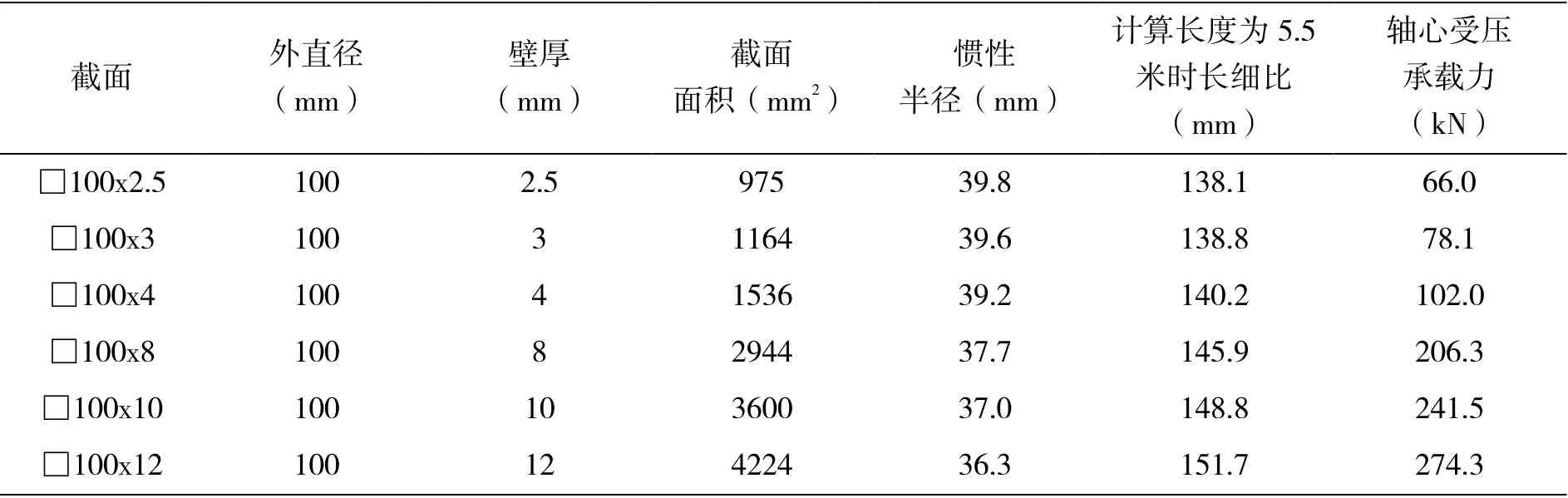
表1 不同壁厚矩形钢管惯性半径与承载力统计表(Q235)

从上表中可以看出，当矩形钢管外尺寸不变时，壁厚越大，惯性半径越小，同等计算长度时长细比越大，但由于截面面积增大，其轴心受压承载力呈曲线上升趋势（图1）。其中□100x12长细比达到151.7，超过了《钢结构设计标准》（GB 50017-2017）7.4.6条规定的受压构件容许长细比值150。

图1 不同壁厚矩形钢管惯性半径及轴心受压承载力变化图

如某案例，桁架构件轴心压力设计值150kN，从轴心受压承载力角度考虑，□100x8、□100x10、□100x12均满足要求，但从容许长细比角度考虑时，□100x12不能满足要求。即使《钢结构设计标准》7.4.6条第2款规定了“轴心受压构件的长细比不宜超过表7．4．6规定的容许值，但当杆件内力设计值不大于承载能力的50%时，容许长细比值可取200。”但在本案例中，□100x12的轴心受压承载力为274.3kN，不满足“轴力设计值不大于承载力的50%”的条件，并不适用该条款，因此□100x12不能满足该桁架构件的设计要求。

当然，增大矩形钢管的截面长宽尺寸也能解决上述问题。但在实际工程中，由于考虑施工简便、简化节点构造、内力传递等原因，常常将梁、柱、桁架中的杆件截面长宽尺寸设计为一致。如矩形钢管桁架中，弦杆和腹杆截面长宽一致时，可保证轴力直接通过壁板间的焊缝传递，此时，轴力较大的弦杆可采用较厚的矩形钢管，轴力较小的腹杆则可采用较薄的矩形钢管。鉴于上述原因，当弦杆采用较大的壁厚时，则极有可能导致其长细比超出规范规定的容许长细比。很多设计人员随手将杆件加厚，自以为安全，其实并不符合《钢结构设计标准》的要求。施工单位也往往因为材料采购等原因，采用厚矩形钢管代替薄矩形钢管，其实也违反了《钢结构设计标准》相关规定。

3 理论分析

笔者查阅相关资料发现，各国规范设置容许长细比规定的目的，主要有两点：一是防止构件在制作、运输和安装过程中发生弯曲；二是防止构件在使用过程中由于自重、振动等原因发生弯曲，并在压力的二阶效应下增大弯曲，进而发生失稳直至完全破坏。因此，可以理解为对轴心受压构件容许长细比的规定，是保证其有一定的抗弯刚度，控制其初始变形，防止其快速进入失稳状态。

那么，实际工程中，同样长度时，较厚的矩形钢管是否柔度更大，更容易发生弯曲变形呢？笔者首先从理论出发，对表1中的6种构件进行运输和起吊阶段的弯曲变形计算，图2模拟构件在起吊时的受力状态，图3模拟构件在运输时的受力状态，前者按照起吊速度取1.3倍动力系数，后者考虑路面颠簸取1.5倍动力系数，经过计算，同一杆件运输状态的最大挠度均小于起吊状态的最大挠度，限于篇幅故仅统计起吊状态的最大挠度，见表2。

图2 起吊时的受力模型

图3 运输时的受力模型

表2 不同壁厚矩形钢管起吊时的最大挠度

由表2可知，上述杆件在起吊时的最大挠度随着壁厚的增加而增加，挠度的增长幅度大于长细比的增长幅度，这是由于壁厚的增加对重量增大的贡献比较显著，对惯性矩增大的贡献相对不显著，对惯性半径增大的贡献也不显著。而构件起吊、运输时的荷载与其自重高度相关，因此壁厚越大挠度越大。因为杆件在运输、起吊阶段的弯曲变形以弹性变形为主，外力撤除后，杆件的弯曲变形有一定程度的恢复，因此需要进一步实践验证。

4 实践验证

制作Q235矩形钢管160x20一根，长度12.1m，两端按铰接考虑，长细比207，已采取防止端部局部受压变形的措施，该矩形钢管构件出厂时最大挠度23mm，满足规范要求故不进行矫直，经过图2的吊装操作和图3的运输操作，再按图4示意搁置在间距12m的角钢支座上，此时肉眼观测时弯曲不明显，但实测最大挠度为68mm，超过《钢结构工程施工质量验收标准》（GB 50205-2020）8.5.1条的规定，为模拟工程最不利条件，该挠度作为初始弯曲不加矫正直接进行试验。该矩形钢管构件一端顶在固定墙上，另一端采用千斤顶缓慢施加轴心压力， 当压力升至280kN即达到设计承载力的50%时，测得最大挠度为102mm。原计划继续增压至560kN，每增加20 kN测量一次最大挠度，但增压至500kN时，构件已发生明显弯曲，为安全起见，停止加压，试验终止，挠度与压力的关系见图6。

图4 矩形钢管受压试验模型图

图5中可以看出，构件变形突变的时机出现在压力值380kN，此时挠度为139mm。构件内附加弯矩达52.82 kN.m，构件边缘理论最大应力为195 N/mm2，实测最大应力为237N/mm2，即构件边缘的部分钢材已经进入屈服阶段，恰好印证了构件变形突然增大的观测结果。

图5 矩形钢管受压挠度变化图

不可否认，该试验采用样本数单一，初始变形的测量精度也不高，试验结果有较高的随机性，但其与理论分析结果基本吻合，即轴向压力与初始变形共同作用时，构件边缘会过早进入屈服状态，从而影响细长杆件的轴心受压承载力。证明了厚壁矩形钢管细长杆在制作、运输、使用阶段累积了较大的初始变形，该初始变形在压力的二阶效应下，使构件边缘的钢材提早进入屈服状态，极大的减小了构件的极限承载力，降低了构件的可靠度，给工程带来了一定的安全隐患。

为进一步验证上述论点，笔者在钢结构加工车间和安装工地进行了随机取样分析。具体工作分为以下几步：1）联系加工厂和就近工地，选取了某矩形钢管桁架中4种矩形钢管，杆件弯矩设计值均为0，每种3~5根，共计15根。2）在加工厂装车前第一次检测平直度，安装完成后第二次检测平直度，结构受力后第三次检测平直度。5）计算4种矩形钢管在起吊运输过程中的理论最大挠度增加值，与实际最大挠度增加值相比较。

初步得出结论是，15根杆件中有2根杆件实际最大挠度增加量超过计算挠度增加量，其实际最大挠度增加量分别是计算挠度增加量的1.24倍、1.13倍。由于实际工程中的矩形钢管都是满足容许长细比的，其初始变形也都小于规范容许值，构件边缘应力值均小于屈服强度的60%，因此无安全隐患。

5 结论及建议

经过理论分析、试验验证和工程实测，证明了增加矩形钢管的壁厚，会导致其长细比和自重增大，在运输、起吊、自重受力等状况下的初始变形也会增大，进而导致矩形钢管构件在压力的二阶效应下进一步弯曲，若该构件长细比大于容许长细比，则构件极易屈曲，存在极大的安全隐患。因此，对采用了受压矩形钢管构件的工程建议如下：

1）所有受压矩形钢管构件在出图前，必须进行专门的容许长细比验算。

2）所有受压矩形钢管构件需要变更厚度时，必须经过设计单位验算并认可。

3）受压矩形钢管构件应在出厂前、吊装前、安装后三个时机严格检查平直度，不得超过规范和设计允许值，否则应就地矫直或返厂矫直。

除矩形钢管存在以上安全隐患之外，壁厚较大的圆钢管构件、腹板厚度较大的工字型截面构件，也存在增加壁厚或腹板厚度时，自重增加较多且抗弯刚度增加较少的情况，该问题也应进行深入研究。