基于改进VMD和TWSVM的多点泄漏检测方法

郎宪明， 王佳政， 曹江涛， 李 平， 蔡再洪

(1. 辽宁石油化工大学 信息与控制工程学院， 辽宁 抚顺 113001； 2. 东北大学 信息科学与工程学院， 沈阳 110819； 3. 沈阳仪表科学研究院有限公司， 沈阳 110043；4. 北京海福润科技有限公司， 北京 100000)

目前，石油、天然气、工业流体等输送主要采用管道运输。为了监控管道运行情况，泄漏检测系统已经广泛应用于管道输送企业[1-2]。然而，多数管道泄漏检测系统只是针对单点泄漏而设计的，当管道局部受压力、震动、腐蚀等影响，会同时出现2点以上的泄漏点，此时单点泄漏检测方法往往失效。因此，进行多点泄漏检测的研究具有实际工程意义。

泄漏信号分析与处理主要体现在单点泄漏信号消噪上[3-4]。Hilbert-Huang变换通过收集管道首末站获得的泄漏声发射信号进行去噪处理，进而提高了单点泄漏定位的精度[5]。针对压力信号下降缓慢的缺点，提出了一种压缩感知的泄漏负压波信号处理方法，将压力信号进行压缩感知变换，进而突出泄漏声波信号的突变点信息。针对管道采集的负压波信号存在大量噪声的问题，提出采用低通滤波、小波滤波和多种滤波方法相结合的形式，实时、高精度地对管道两端的压力信号进行滤波，保证泄漏信息不被滤除[6]。由于小波去噪需要根据经验选择合适的小波基函数，而经验模态分解(empirical mode decomposition，EMD)具有不用选择基函数的优点，采用基于EMD的方法进行管道泄漏检测，从而有效提取管道泄漏信号的拐点信息，以减小噪声的影响[7]。变分模态分解(variational mode decomposition，VMD)相比EMD[8]，具有避免信号模态混叠的优点。通过迭代搜索变分模型的最优解，选择分解后的频率中心和带宽。因此，虽然VMD具有显著的泄漏信号和噪声分离效果和能有效地抑制模型混叠的优点，但VMD方法存在模态分解个数需要依据经验进行设置的不足。

由于大多数泄漏检测研究只针对单点泄漏进行的[9-14]，当管道同时发生多个泄漏时，产生的瞬态声信号更为复杂，泄漏信号之间的相互影响，以及管道外部噪声叠加在管道泄漏声波信号上，从而影响管道中瞬态声波信号的衰减规律，进而在混合泄漏声波信号条件下，无法有效地去除泄漏信号的噪声。因此，对多点泄漏声波信号进行有效的特征提取是多点泄漏检测的关键问题。

基于支持向量机(support vector machine, SVM)、最小二乘支持向量机(least squares support vector machine, LSSVM)和双支持向量机(twin support vector machine, TWSVM)的管道泄漏检测方法得到了广泛的研究[15-18]。通过建立管道泄漏声波信号和发生泄漏之间的数学关系，进行管道泄漏检测的有效识别。由于TWSVM相比SVM，在算法的运行速度和识别准确率均高于SVM。因此，本文采用TWSVM对管道多点泄漏进行检测。

1 改进VMD方法

1.1 VMD算法

基于VMD的多点泄漏检测方法，需要建立多点泄漏声波信号的变分模型，利用求解约束变分方程最优解的过程来实现多点泄漏信号的分解。在变分模型的求解过程中，各模态的中心频率不断更新，最终分解出k个固有本征模态函数(intrinsic mode function，IMF)。VMD能提取多点泄漏信号的低频有效泄漏信号，滤除外界高频噪声。VMD分解过程如下

(1)

式中：x(t)是原始泄漏声波信号；uk是变分模态函数;δ(t)是单位阶跃函数;ωk是变分模态函数对应的中心频率。

uk=Ak(t)cos(2πωk(t))

(2)

式中，Ak是瞬时振幅。

为了得到上述约束变分问题的最优解，采用了增广拉格朗日函数，构造的增广拉格朗日函数如下

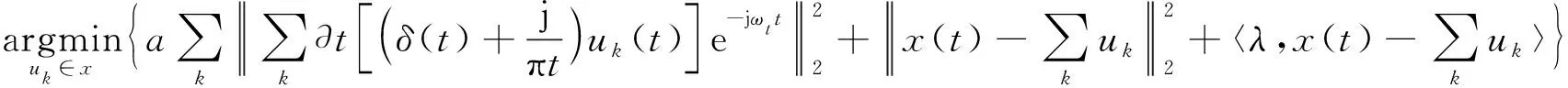
(3)

式中：a是带宽参数；λ是拉格朗日乘子。

通过交替方向乘子法计算增广拉格朗日函数，并将原始多点泄漏声波信号分解为k个固有本征模态函数。

然后，根据Plancherel定理，将L2范数问题等距变换为Fourier变换，得到如下公式

(4)

(5)

其收敛条件如下

(6)

1.2 VMD结合误差能量算法

提出了一种自适应方法计算本征模态函数有效数目。采用重构信号的误差能量函数作为自适应分解模态数目的判断依据。

多点泄漏声波信号采用VMD进行分解时，首先，确定合适的模态分解个数n。因为n决定了频率分辨率，如果n太小，就会本征模态函数分解不足，对泄漏声波信号微小波动的信号不敏感，如果n太大，就会产生伪本征模态函数分量，增加计算量。

假设采集的多点泄漏声波信号为x(t)。x(t)经VMD分解为k个模态函数，计算如下

(7)

式中，τ是原始多点泄漏声波信号与经VMD重构信号之间的误差。

定义误差能量函数如下

Eτ=τ2

(8)

误差能量越小，说明原始多点泄漏声波信号与重构信号越相似。如果误差能量为0，则原始多点泄漏声波信号和重构信号相同。

针对经典VMD算法的不足，本文对VMD算法进行了如下改进：

(1) 首先，设置VMD分解级别为n：如果n值太大，则会增加计算量，并可能产生伪模态分解。如果n设置得太小，可能产生模态分解不足。

(2) 多点泄漏声波信号经VMD后，得到了大量的本征模态函数。

(3) 每个固有本征模态函数通过误差能量函数计算。

(4) 计算每种本征模态函数的误差能量函数。

(5) 绘制误差能量图，首先计算阈值，即所有误差能量函数的平均值。一般情况下，每种模式的误差能量远小于阈值θ，称为有效本征模态模式。当误差能量接近θ时，说明了固有本征模态函数已包含了多点泄漏的有效信息。

因此，根据改进的VMD，通过设置阈值θ，自适应的选择合适数量的模态函数。

2 多点泄漏检测方法

2.1 特征提取

当管道发生多点泄漏时，管道首末站收集到的泄漏声波信号中包含了大量的多点泄漏信息。泄漏声波的平均幅值可以反映多次泄漏引起的声波大小，泄漏声波的能量可以用来计算声波振幅强度，泄漏声波的有效值可以用来表示声波信号的振动能量。另外，泄漏声波的峰值系数可以用来表示声波信号的幅度变化，泄漏声波的脉冲系数可以用来反映多次泄漏下声波的变化特征。此外，还利用泄漏声波的峰值来计算声波振幅的分布。因此，根据式(9)～式(14)计算多点泄漏的特征参数。

(9)

(10)

(11)

(12)

(13)

(14)

式中：zi是泄漏声波信号的幅值；h是采样点幅值；Z1、Z2、Z3、Z4、Z5和Z6分别是平均幅值、能量、有效值、峰值系数、脉冲系数和峰值。

通过对多点泄漏声波信号的时域特征分析，采用以上6个特征值作为多点泄漏声波信号的特征值。

2.2 双支持向量机

TWSVM的目标是构造一对对偶问题，每一类通过优化一对超平面上的二次规划问题(quadratic programming problems (QPPs))使其更接近相近的平面，同时与另一平面具有足够的距离。

令具有一类样本X1∈Rq×v,和另一类样本X2∈Rp×v,q和p分别是样本的个数，v是每个样本的属性个数。

非平行超平面对的计算如下

(15)

式中：ω1和ω2是非平行超平面的法向量；b1和b2是偏置。

TWSVM的对偶问题表示为

s.t.-(X2ω1+e2b1)+ξ≥e2,ξ≥0

(16)

s.t.-(X1ω2+e1b2)+η≥e1,η≥0

(17)

其中c1>0和c2>0是参数，ξ和η是松弛向量，并且e1和e2是适当的维数向量。

利用Karush-Kuhn-Tucker(KKT)条件，可以求解对偶问题的解。因此，通过建立的多点泄漏检测的TWSVM模型后，待测多点泄漏声波信号数据由决策函数决定共i个泄漏点，决策函数如下

classi=min|XTωi+bi|i=1,2，…,m

(18)

2.3 多点泄漏检测方法

通过现场采集的泄漏声波信号，对其进行特征提取，作为TWSVM的输入，通过离线学习建立多点泄漏识别模型。然后，通过实时采集的声波信号，对其进行多点泄漏识别。基于改进VMD和TWSVM的多点泄漏检测方法流程图如图1所示。

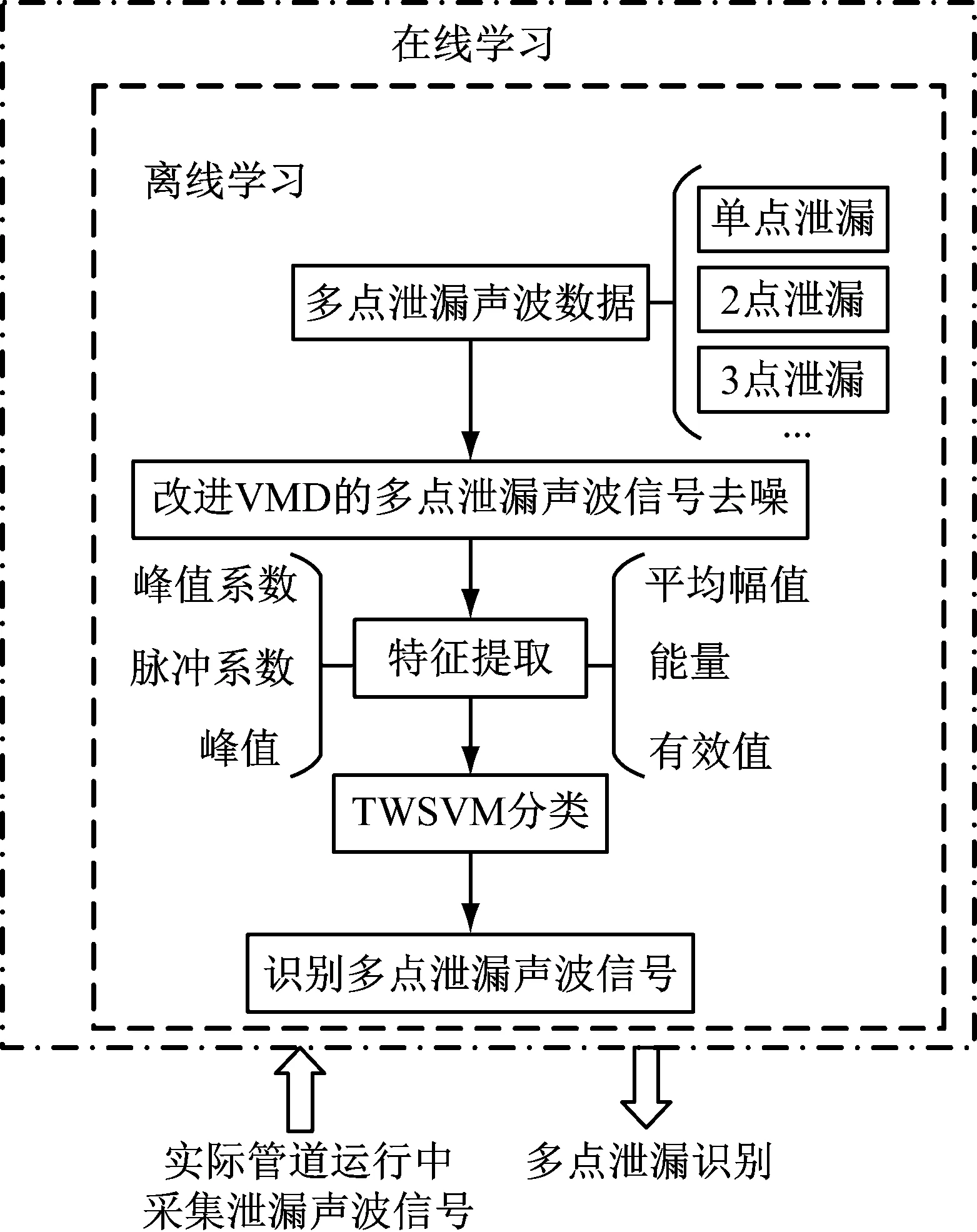
图1 基于改进VMD和TWSVM的多点泄漏检测方法流程图Fig.1 Flow chart of multiple leaks detection method based on improved VMD and TWSVM

从图1可以看出，首先，利用改进VMD算法对管道首末站采集的多点泄漏声波信号进行消噪。然后，消噪后的泄漏声波信号经选取的平均幅值、能量、有效值、峰值系数、脉冲系数、峰值共6个特征值组成特征向量，并将特征向量作为TWSVM的输入，进行多点泄漏识别。

3 仿 真

为了安全起见，用水代替油来在环形管道进行多点泄漏模拟测试。多点泄漏信号采集装置如图2所示。管道首末站采用PCB 106B声波信号传感器采集多点泄漏声波信号，环形管道全长2 800 m，管道内径50 mm，流量12 m3/h，环形管道中在不同位置安装不同孔径的泄漏球阀模拟多点泄漏，环境温度为25 ℃，水的密度为997 kg/m3。管道首站压力为0.8 MPa，末站压力为0.2 MPa。声波信号采样频率为1 000 Hz。试验中，所提方法在MATLAB 2014a和LabView环境下进行了测试。

图2 试验设备Fig.2 Test apparatus

当管道首站压力为0.8 MPa，末站压力为0.2 MPa时，外界环境温度为25 ℃时，在距离管道首站1 000 m的位置，打开孔径为2 mm的阀门模拟单点泄漏，在首站的PCB 106B传感器实时采集管道内声波信号，并通过NI cDAQ9181数据采集卡将声波信号传送到上位机进行数据显示，其单点泄漏声波信号如图3所示。

图3 首站采集的单点泄漏声波信号Fig.3 Acoustic wave signal under single leak of upstream

从图3中可以看出，在0.9 s时，首站PCB 106B传感器获得的泄漏声波信号出现一个明显的声波信号下降。大约在1.5 s时，声波信号恢复平稳状态。

当管道首站压力为0.8 MPa，末站压力为0.2 MPa时，外界环境温度为25 ℃时，在距离管道首站1 000 m和1 200 m位置的位置，同时打开孔径为2 mm和3 mm的阀门模拟2点泄漏，在首站的PCB 106B传感器实时采集管道内声波信号，其2点泄漏声波信号如图4所示。

图4 首站采集的2点泄漏声波信号Fig.4 Acoustic wave signal under two leaks of upstream

从图4中可以看出，在2.3 s时，首站PCB 106B传感器获得的泄漏声波信号出现一个明显的声波信号下降。大约在3 s时，声波信号恢复平稳状态。

当管道首站压力为0.8 MPa，末站压力为0.2 MPa时，外界环境温度为25 ℃时，在距离管道首站1 000 m、1 200 m和1 400 m位置同时打开孔径为2 mm、3 mm和4 mm的阀门模拟3点泄漏，在首站的PCB 106B传感器实时采集管道内声波信号，其3点泄漏声波信号如图5所示。

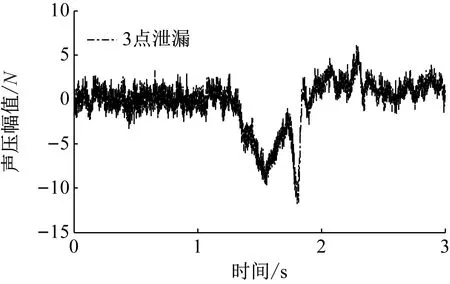
图5 首站采集的3点泄漏声波信号Fig.5 Acoustic wave signal under three leaks of upstream

从图5中可以看出，在1.2 s时，首站PCB 106B传感器获得的泄漏声波信号出现一个明显的声波信号下降。大约在2 s时，声波信号恢复平稳状态。

从图4和图5可以看出，2点泄漏和3点泄漏发生时，泄漏声波的声压幅值的波动幅度相比单点泄漏更加明显，但是由于泄漏声波信号容易被外界噪声污染，而且从首站获取的泄漏声波波形中无法区分每个泄漏点到达首站PCB 106B传感器感知泄漏声波变化的准确时间。

根据采用PCB 106B传感器现场获取的3点泄漏声波信号，利用VMD对其进行5层IMFs分解。其3点泄漏声波信号的IMFs和频谱如图6和图7所示。

图6 3点泄漏声波信号经VMD分解后获得的IMFsFig.6 IMFs obtained by VMD decomposition of three leaks acoustic wave signal

图7 3点泄漏声波信号经VMD分解后的频谱图Fig.7 Spectrum obtained by VMD decomposition of three leaks acoustic wave signal

根据3点泄漏声波信号的5层VMD分解，按照式(7)和式(8)分别计算其误差和能量函数。同理，根据单点泄漏声波信号5层VMD分解和2点泄漏声波信号的5层VMD分解，绘制误差能量图，其VMD的不同IMFs分解数对应的误差能量图如图8所示。

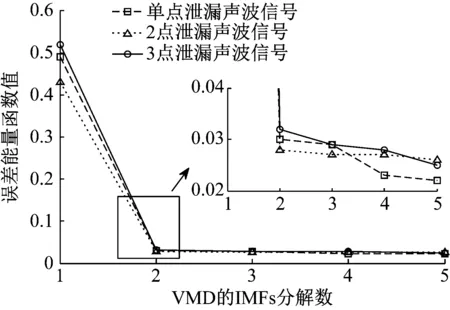
图8 VMD的不同IMFs分解数对应的误差能量图Fig.8 Error energy diagram of IMFs for VMD

从图8可以看出，当单点泄漏经VMD消噪时，选择2个IMFs时，误差能量函数值为0.03。根据式(8)，泄漏声波信号与重构信号差值的能量函数是0.03，说明重构信号能表征单点泄漏声波信号，也就是说明2个IMFs中包含了单点泄漏的大部分信息。同理，当2点泄漏经VMD消噪时，选择2个IMFs时，误差能量函数值为0.028。根据式(8)，泄漏声波信号与重构信号差值的能量函数是0.028，说明重构信号能表征2点泄漏声波信号，也就是说明2个IMFs中包含了2点泄漏的大部分信息。当3点泄漏经VMD消噪时，选择2个IMFs时，误差能量函数值为0.032。根据式(8)，泄漏声波信号与重构信号差值的能量函数是0.032，说明重构信号能表征2点泄漏声波信号，也就是说明2个IMFs中包含了3点泄漏的大部分信息。因此，我们可以设定阈值θ为0.05，选择2个IMFs分别对单点、2点、3点泄漏声波信号进行信号重构。

为了对比改进VMD与EMD对泄漏声波的消噪效果，EMD算法根据现场测试漏声波去噪效果情况，单点、2点、3点泄漏声波信号经EMD分解，分别产生12个IMFs，由于泄漏声波信号主要体现在低频特性，对其包含高频分量的IMFs进行剔除，分别选择6至12个IMFs进行单点、2点、3点泄漏声波信号重构。其原始泄漏声波信号、经改进VMD消噪的信号和经EMD消噪的信号对比波形曲线分别如图9、图10和图11所示。

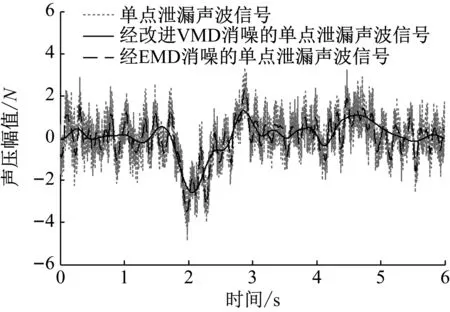
图9 单点泄漏声波消噪信号的对比波形Fig.9 Comparison waveform of single leak acoustic wave after denoise

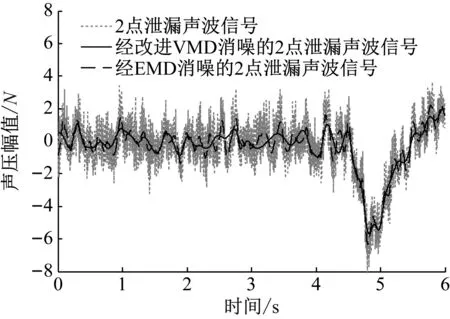
图10 2点泄漏声波消噪信号的对比波形Fig.10 Comparison waveform of two leaks acoustic wave after denoise

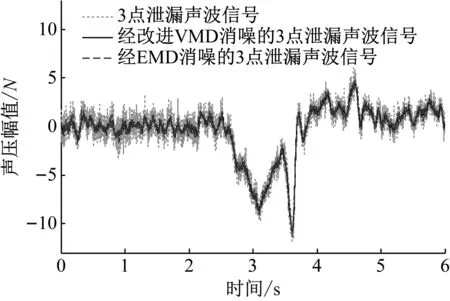
图11 3点泄漏声波消噪信号的对比波形Fig.11 Comparison waveform of three leaks acoustic wave after denoise

从图9～图11可以看出，经改进VMD消噪的泄漏声波信号较好的恢复了原始泄漏信号特征，相比EMD消噪的效果，重构信号曲线更加平稳，有效的保留了多点泄漏信号的特征。

经改进VMD消噪后的单点、2点、3点泄漏信号进行特征提取，特征值分别按照式(9)～式(14)进行计算。将平均幅值、能量值、有效值、峰值因子、峰值系数和峰值共6个特征值组成特征向量，作为TWSVM的输入，将单点、2点、3点泄漏个数作为TWSVM的输出，TWSVM通过训练，获得离线多点泄漏识别模型。其中一组不同泄漏点的特征值如图12所示。

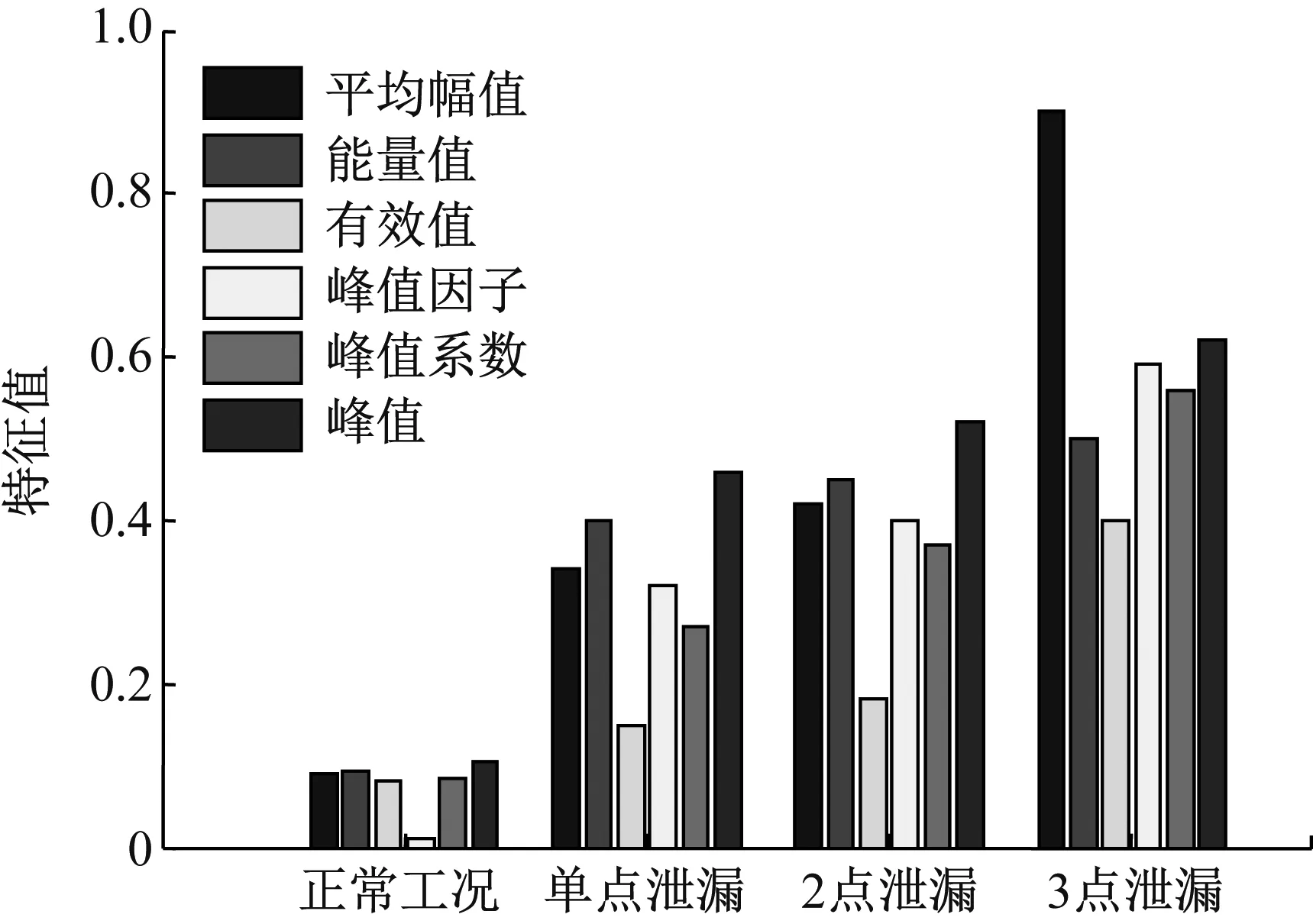
图12 多点泄漏声波信号的特征值Fig.12 The feature values of different multiple leaks

从图12中可以看出，单点泄漏、2点泄漏和3点泄漏的各个特征值是不同的。通过现场试验，正常工况下的平均幅值、能量值、有效值、峰值因子、峰值系数和峰值相比单点泄漏、2点泄漏和3点泄漏的特征值小；泄漏声波的平均幅值、能量值、有效值、峰值因子、峰值系数和峰值随着泄漏点的增多逐渐增大，其3点泄漏声波产生的特征值相比单点、2点泄漏声波的特征值大。

由于TWSVM是一种智能识别算法，可以将泄漏声波的平均幅值、能量值、有效值、峰值因子、峰值系数和峰值共6个特征值组成特征向量，作为TWSVM的输入，将多点泄漏的个数作为TWSVM的输出，对管道的多点泄漏进行识别。

在管道多点泄漏模拟试验中，首站的PCB 106B传感器实时采集管道内声波信号，采样率为1 000 Hz。管道首站压力为0.8 MPa，末站压力为0.2 MPa时，外界环境温度为25 ℃时，采集正常工况下的声波信号500组；在距离管道首站1 000 m位置打开孔径为2 mm的阀门模拟单点泄漏，采集管道内单点泄漏声波信号500组；在距离管道首站1 000 m和1 200 m位置打开孔径为2 mm和3 mm的阀门模拟2点泄漏，采集管道内2点泄漏声波信号500组；在距离管道首站1 000 m、1 200 m和1 400 m位置同时打开孔径为2 mm、3 mm和4 mm的阀门模拟3点泄漏，采集管道内3点泄漏声波信号500组。采用改进的VMD方法对获取的正常工况、单点、2点、3点泄漏声波信号进行消噪。通过2个IMFs分别进行正常工况、单点、2点、3点泄漏声波信号的重构。同时，EMD算法分别选择6～12个IMFs进行正常工况、单点、2点、3点泄漏声波信号重构。对每组声波重构信号分别进行特征提取，组成特征值。因此，组成的特征值样本共2 000组(正常工况、单点泄漏、2点泄漏和3点泄漏试验样本各500组)，其中每种工况样本的400组作为TWSVM的学习特征向量，余下的特征向量作为TWSVM的测试集。将TWSVM的参数设置为c1=0.2,c2=0.2,和σ=0.01, 误差设定为1×10-5。采用支持向量机和最小二乘支持向量机进行多点泄漏识别对比分析，其中libsvm松弛变量和核参数分别设置为2和1。最小二乘支持向量机采用LSSVMlab，其松弛变量和多分类器的核参数分别设置为2和1。其不同方法的泄漏检测结果如表1所示。

从表1可以看出，在正常工况下，声波信号经改进VMD消噪结合SVM、LSSVM、TWSVM的识别准确率相比声波信号经EMD消噪结合SVM、LSSVM、TWSVM的识别准确率高，其改进VMD消噪结合TWSVM的识别准确率达到98%；在单点泄漏工况下，单点泄漏声波信号经改进VMD消噪结合SVM、LSSVM、TWSVM的识别准确率相比声波信号经EMD消噪结合SVM、LSSVM、TWSVM的识别准确率高，其改进VMD消噪结合TWSVM的识别准确率达到98.4%；在2点泄漏工况下，2点泄漏声波信号经改进VMD消噪结合SVM、LSSVM、TWSVM的识别准确率相比声波信号经EMD消噪结合SVM、LSSVM、TWSVM的识别准确率高，其改进VMD消噪结合TWSVM的识别准确率达到98.4%；在3点泄漏工况下，3点泄漏声波信号经改进VMD消噪结合SVM、LSSVM、TWSVM的识别准确率相比声波信号经EMD消噪结合SVM、LSSVM、TWSVM的识别准确率高，其改进VMD消噪结合TWSVM的识别准确率达到97.8%。因此，改进VMD消噪结合TWSVM在正常工况、单点泄漏、2点泄漏和3点泄漏工况的识别准确率分别为98%、98.4%、98%和97.8%。由于改进VMD比EMD在多点泄漏声波信号去噪效果上，能更好的保留多点泄漏信号特征。根据试验结果可以看出，改进VMD结合TWSVM对多点泄漏进行识别是可行的。

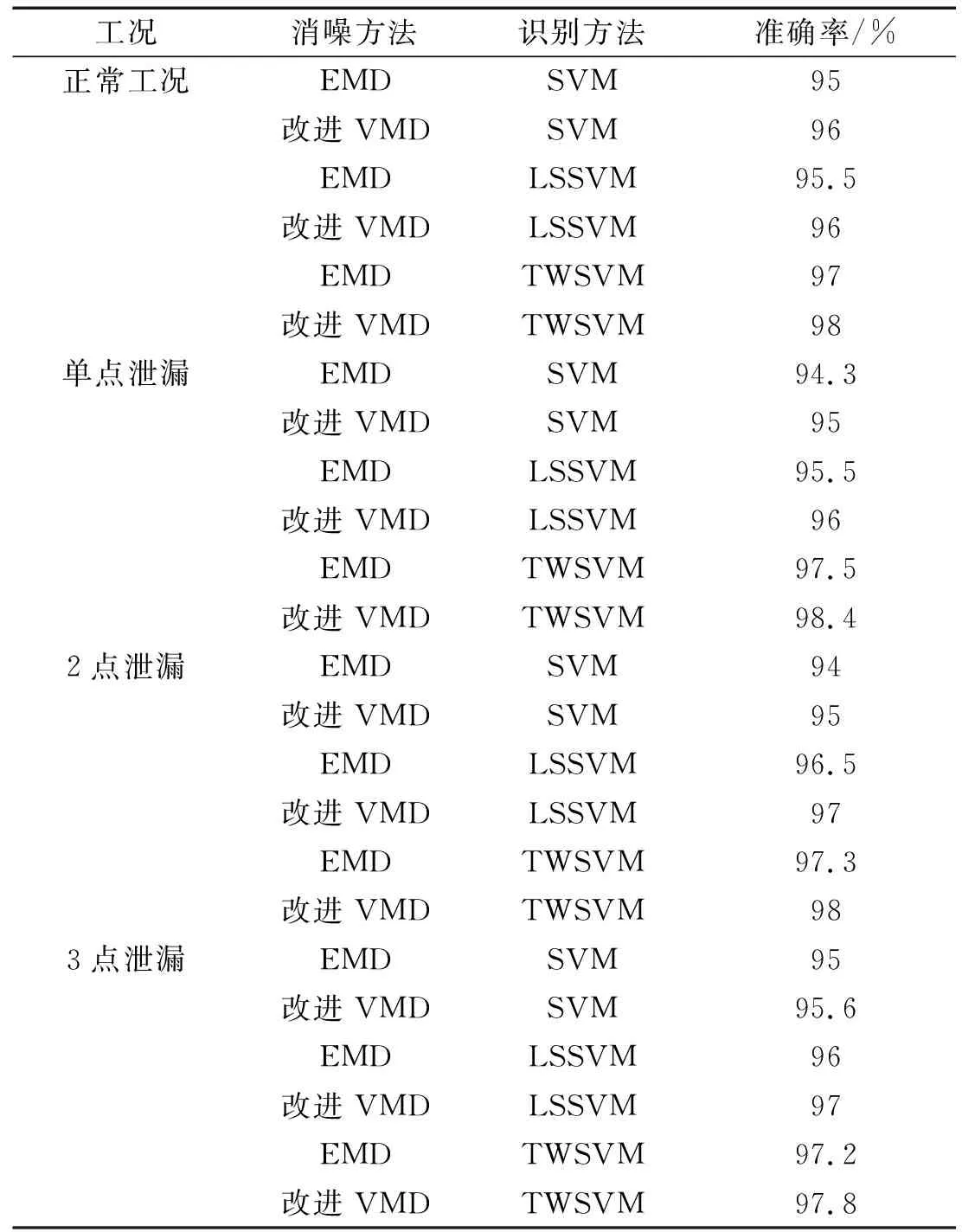
表1 不同方法的多点泄漏检测结果Tab.1 Comparison of the different models’multiple leaks detection results

4 结 论

由于管道同时发生多点泄漏时，各个泄漏点的声波信号相互叠加，影响泄漏声波传播规律，不能有效检测多点泄漏。改进VMD算法通过采用误差能量函数自适应选择IMFs个数，相比EMD对多点泄漏声波信号去噪效果更能保留多点泄漏信号特征。将消噪后的多点泄漏声波信号按照平均幅值、能量值、有效值、峰值因子、峰值系数和峰值计算特征值并组成特征向量，随着泄漏点数的增多，相应的特征值也相应增大。通过环形管道试验，改进VMD结合TWSVM的单点泄漏识别准确率达到98.4%，2点泄漏识别准确率达到98%，3点泄漏识别准确率达到97.8%。说明改进VMD结合TWSVM有较好的多点泄漏识别效果。在多点泄漏识别准确率的基础上，设计多点泄漏定位算法是后续的研究工作的重点。