微缝卷曲耦合低频吸声超材料研究

吴 飞， 陈文渊， 巨泽港， 姚凌云， 胡 嫚

(1. 重庆大学 机械与运载工程学院， 重庆 400715； 2. 西南大学 工程技术学院， 重庆 400715)

由多孔纤维材料等制成的传统吸声体是一种有效的噪声吸收结构，但往往需要具有与工作波长相当的结构厚度，这严重阻碍了其在低频范围内的应用。声学超材料作为一种新型的人工复合结构材料，拥有自然材料所不具备的超常物理特性，如负等效质量密度，负等效弹性模量，负折射率等。近年来声学超材料的迅速发展使其能够以多种方式对声波进行控制[1-2]。其中，在2012年首次被提出的空间卷曲型声学超材料[3]凭借其优异的低频吸声性能，亚波长结构厚度等特点引起了众多研究人员的关注。目前普遍采用的一种方法是在空腔内构建卷曲通道，增加声波的有效传播长度从而减小吸声结构厚度，实现对低频噪声的吸收。基于此，Li等[4]设计了一种总厚度仅为工作波长1/223的低频吸声器。Donda等[5]最新研究的超薄低频吸声器能在结构厚度仅为13 mm的条件下实现在50 Hz处的准完美吸声，此时结构厚度为工作波长的1/527。此外在固定厚度下，通过改变卷曲通道参数能对结构的吸声性能进行调节。Liang等[6-8]设计了一种具有良好吸声性能与丰富可调性的单通道入口卷曲迷宫型吸声结构，该结构因声波入口处面积较大，无法提供足够的声阻，需要额外添加多孔吸声材料(如棉花，吸声海绵等)来补充声阻从而提高吸声系数实现高效吸声。当面临严苛的工作环境，如在高温、潮湿等条件下，该类吸声结构的实际应用会受到一定的制约。为了促进声学超材料在工程中的实际应用，本文在卷曲通道型吸声结构的声波入口处引入微缝设计。微缝与微穿孔类似，都可作为良好的吸声原件而被应用，其声阻抗理论公式也都存在，当微缝宽度减小至丝米级时，其阻抗比将超过1，此时微缝可以提供足够的声阻来实现高效吸声，从而不再需要额外添加吸声材料[9-11]。

基于上述研究背景，本文设计了一种微缝卷曲耦合低频吸声超材料，通过建立微缝与卷曲通道的耦合吸声理论模型与有限元模型对结构的吸声性能以及吸声机理进行分析研究，并进行了试验验证。研究结果表明，所设计的吸声超材料在低频范围内具有良好吸收性能，试验结果良好，结构准确可行。该吸声超材料的以上吸声特性使其能够应用于噪声控制工程领域中。

1 耦合吸声理论模型

本文所设计的微缝卷曲耦合吸声超材料由声波入口处的微缝与底部的卷曲通道组成，详细的结构模型与结构表征参数如图1所示。结构的声压反射系数r与吸声系数α可由结构的阻抗理论计算公式求得，即：

(1)

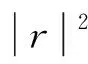
(2)

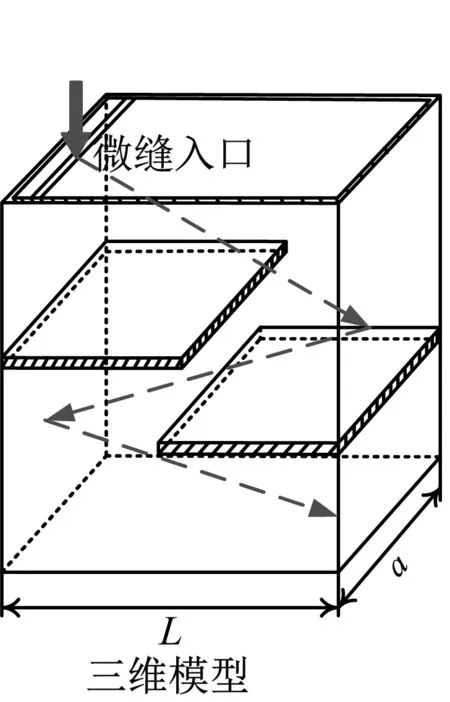
图1 微缝卷曲耦合吸声超材料结构示意图Fig.1 Schematic diagram of micro slit-curl coupling acoustic metamaterial

式中：Z0=ρ0·c0为空气特性阻抗;ρ0和c0分别为空气密度与声速。Zt为整个吸声结构的总阻抗，由微缝Zslit与卷曲通道阻抗Zc串联组成，即：

Zt=Zslit+Zc

(3)

1.1 微缝板声阻抗

根据Tor Erik Vigran所提出的微缝吸声理论[12]，微缝的声阻抗可由下式所得

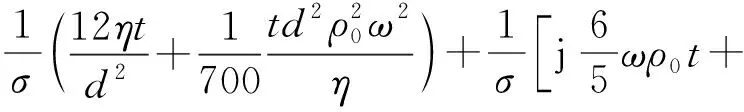
(4)

(5)

式中：Δt是末端修正;d和t分别是缝宽和板厚;σ是穿缝率;η是空气动力黏度,其值为1.81×10-5Pa·s;ω是角频率。

1.2 卷曲通道阻抗

卷曲通道的阻抗Zc可由阻抗转移公式求得，即

Zc=-jZe,ccot(keqleff)

(6)

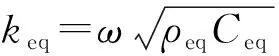
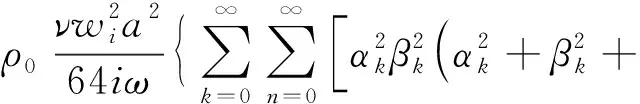
(7)

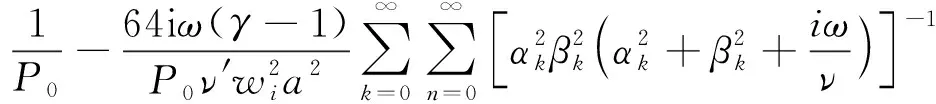
(8)

式中：αk=(2k+1)π/wi和βn=(2n+1)π/a为计算常数，ν=μ/ρ0是空气的运动黏度；ν′=k/ρ0Cv，k和Cv分别是热传导率与定容比热容；P0和γ分别为空气的压力和比热率。

2 有限元模型

微缝卷曲耦合吸声超材料有限元模型在多物理场仿真软件COMSOL Multiphysics5.4a中建立，应用软件内置的压力声学(Pressure Acoustic)模块与热黏性声学(Thermal-Acoustic)模块在频域内进行仿真分析，数值模型如图2所示。其中压力声学模块模拟结构外部声场，热黏性声学模块模拟结构内部声场，微缝表面为两个物理场的耦合边界，定义为声-热黏性声学边界。

在压力声学模块中，声压由亥姆赫兹[17-19]方程(Helmholtz equation)进行控制，即：

(9)

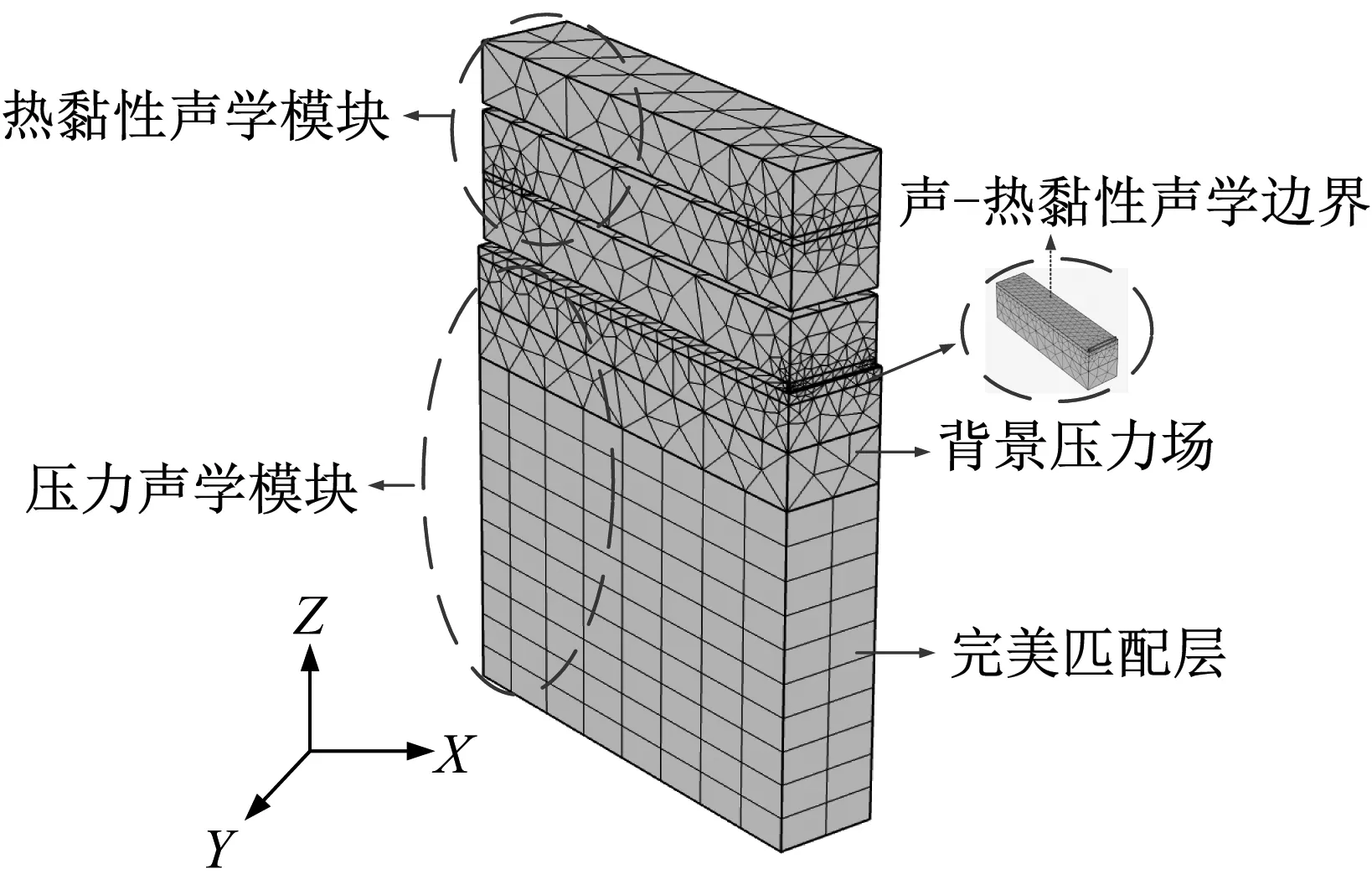
图2 微缝卷曲耦合吸声超材料有限元模型Fig.2 Finite element model of the micro slit-curl coupling acoustic metamaterial

式中：P为声压;t为时间;c0为声速。完美匹配层是可以让入射到该区域的声波完全进入的一种特殊介质层，该层介质的阻抗与相邻介质的阻抗完全匹配。通过设置完美匹配层在背景压力场的末端来模拟无限边界条件和非反射边界条件。背景压力场定义的声压幅值设定为1 Pa，声速为343 m/s，声波由Z轴的正方向垂直入射。

当声波在尺寸狭小的几何结构中传播时，热损耗和黏滞损耗会导致声波衰减，故采用热黏性声学模块对结构内部声场进行仿真分析。在热黏性声学模块中，声压，温度和实际传播速度由三个方程进行控制[20-22]：分别是线性纳维-斯托克斯方程(Navier-Stokes)，质量连续性方程和能量守恒方程，分别如下所示

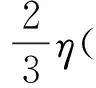
(10)

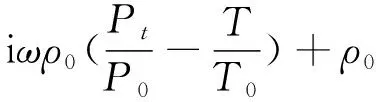
(11)

iω(ρ0CpT-T0α0Pt)=-∇·(-K∇T)

(12)

式中:ut为速度场;T为温度;Pt为t时刻的声压;η为空气动力黏度;Cp为恒压热容;K为导热系数;I为单位矩阵;P0和T0为设定的背景压力和温度。

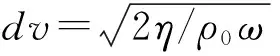
3 吸声性能分析

3.1 低频吸声机理

本小节基于以上建立的耦合吸声理论模型与有限元模型对结构的吸声机理进行分析，理论吸声曲线与数值吸声曲线分别由软件Matlab与COMSOL计算获得，计算结果如图3所示，对应的计算参数如表1所示。

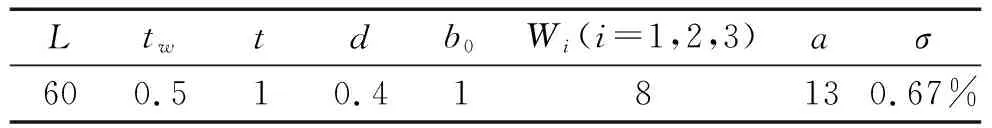
表1 微缝卷曲吸声体参数表Tab.1 Micro slit-curl absorber parameter table mm

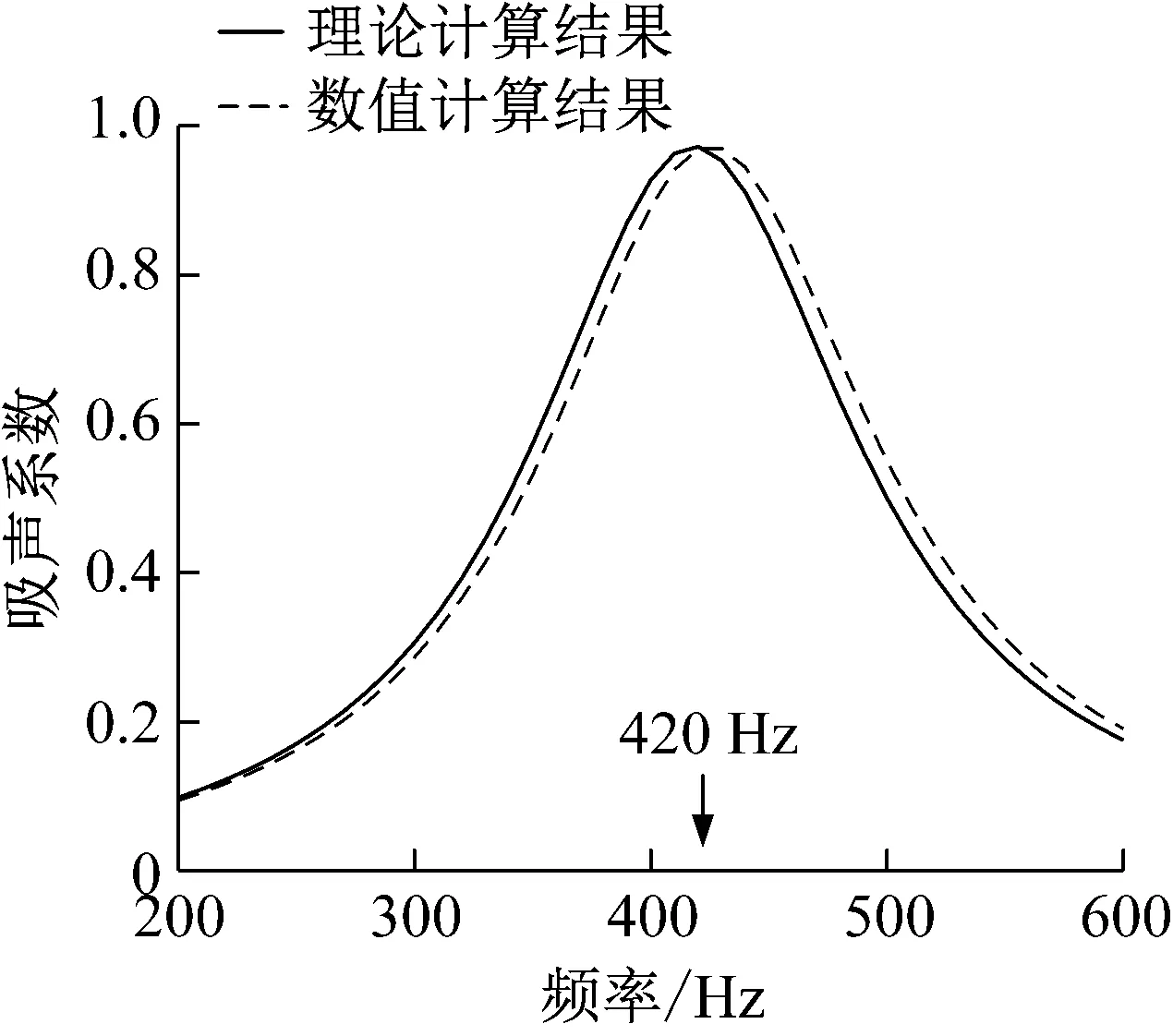
图3 吸声系数的频响曲线Fig.3 Absorption coefficient curve

从图3中可看出该吸声结构在频率420 Hz处达到吸声峰值，此时的吸声系数为0.97，相对吸声带宽为36.8%，展现出了良好的低频吸声性能。此时结构的总厚度为27 mm，为共振频率下对应波长的1/31，具有深亚波长尺度特性。图中理论计算结果与数值计算结果变化趋势一致，能够反映结构的吸声主要频谱特征；二者之间误差较小，结果吻合。产生误差的主要原因是数值模型中的有效传播长度小于理论计算公式中的等效传播长度，导致共振峰左边吸声系数的理论值在同一个频率下高于数值解，共振吸收峰右边的理论计算结果又小于数值计算结果。

为解释该吸声超材料的高效吸声特性，本小节运用阻抗分析法对其吸声机理进行研究。该结构的声阻和声抗分别对应相对声阻抗的实部与虚部，通常情况下，当声抗值为0时对应的频率为结构的峰值频率，结构在此时获得吸声峰值。若此时对应的声阻值等于1，就意味着结构的声阻抗与空气的特性阻抗完全匹配，满足临界耦合吸声条件，结构实现完美吸声，获得的吸声峰值为1。本文所设计结构的相对声阻如图4所示，从图中可看出当声抗值为0时对应的频率为420 Hz，为结构的峰值频率，此时的声阻值为1.37，与1较为接近。以上结果说明该吸声超材料几乎满足临界耦合吸声条件，结构的峰值吸声系数也达到了0.97，实现近完美吸声。

图4 声阻抗图Fig.4 Absorption impedance

3.2 缝宽对吸声性能的影响

本小节通过理论模型与有限元模型分析缝宽对结构吸声性能的影响。首先设定结构的穿缝率σ=1.3%，结构长度L=61 mm，然后将缝宽值分别取0.2 mm，0.4 mm和0.8 mm，剩余的结构参数参照表1中的数据。保持穿缝率不变的条件下，在有限元模型中分别对应4条0.2 mm，2条0.4 mm与1条0.8 mm的微缝。最终得到缝宽对吸声性能的影响规律，具体结果如图5所示，其中不同虚线形式代表不同缝宽条件下的数值解，实线是其对应的理论解。图5中理论计算结果与数值计算结果变化趋势保持一致，能够较为准确的反映缝宽对结构吸声性能的影响规律。结果显示，在穿缝率，结构长度以及其他几何参数不变的条件下，吸声系数随着缝宽的减小而逐渐增大，同时共振频率向高频移动，吸声带宽增加。这是因为随着缝宽减小，结构的相对声阻增加而声抗减小，声阻的增加提高了结构阻抗与空气特性阻抗的匹配程度，从而获得更高的吸声系数，不再需要额外添加吸声材料补充声阻，声抗的减小导致结构的声阻抗比增大，从而能够产生更宽的吸声带宽。

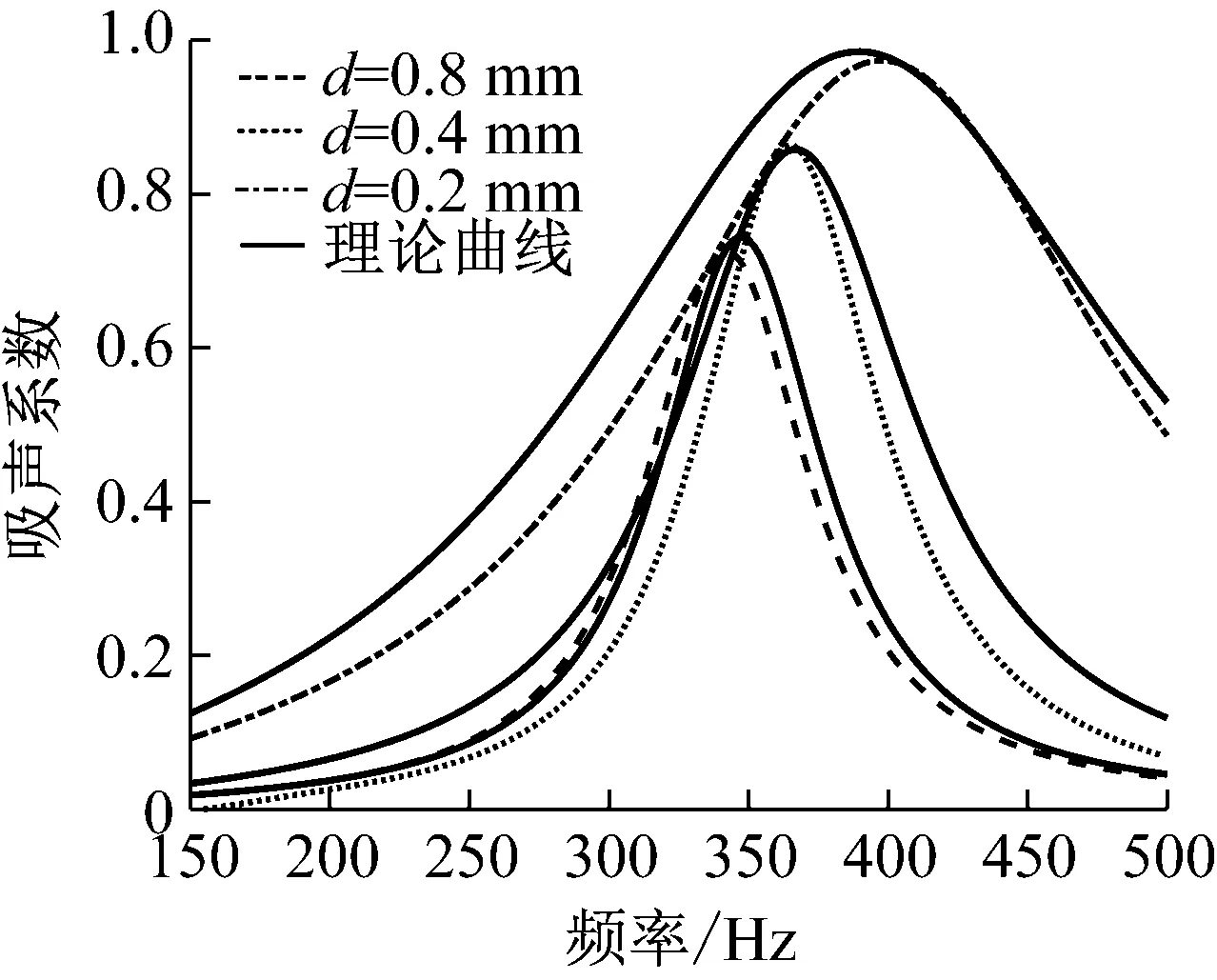
图5 不同缝宽下的吸声系数的频响曲线Fig.5 Absorption coefficient curve with different slit widths

4 试验验证与拓宽吸声带宽

为了验证本文所设计吸声超材料的准确性，本节将进行试验验证。此外，如何拓宽吸声带宽也是低频噪声吸收领域亟待突破的问题之一，目前通常采用并联多个峰值频率不同的结构协同耦合拓宽吸声带宽，本节在进行结构准确性验证的同时也对结构的吸声带宽进行了拓宽试验。本试验采用的测量仪器为B&K4206A型，边长为60 mm的矩形阻抗管，运用双传声法测量结构的吸声系数。微缝板由不锈钢材料制成，卷曲通道由树脂材料通过3D打印制成。试验总共构建了三个样件进行测量，三个样件具有相同的卷曲通道参数配置，具体数值参照表1，设置样件1缝宽为0.4 mm，穿缝率0.67%；样件2缝宽为0.3 mm，穿缝率为2.5%；样件3为样件1,2的并联体，用以拓宽吸声带宽。

图6(a)是试验装置图，图6(b)～(d)为试验结果与数值计算结果的对比图，从中可以看出每个吸声样件的数值计算结果与试验结果基本吻合，二者之间的误差可能来自于制造误差与装配误差。样件1与样件2分别在420 Hz，475 Hz处实现近完美吸声，对应的吸声峰值为0.97与0.98。并联后的结构样件3在420 Hz与475 Hz处取得两个吸声峰值，且都达到了0.9以上，依然能够实现比较好的低频吸声。并联之后的吸声峰值小于单体1单独吸声峰值的原因是样件1，2在进行协同耦合吸声时需要牺牲了部分峰值拓宽吸声带宽。最终拓宽后的吸声带宽达到了49%，实现了在低频范围内的宽带吸声，进一步促进了实际应用。

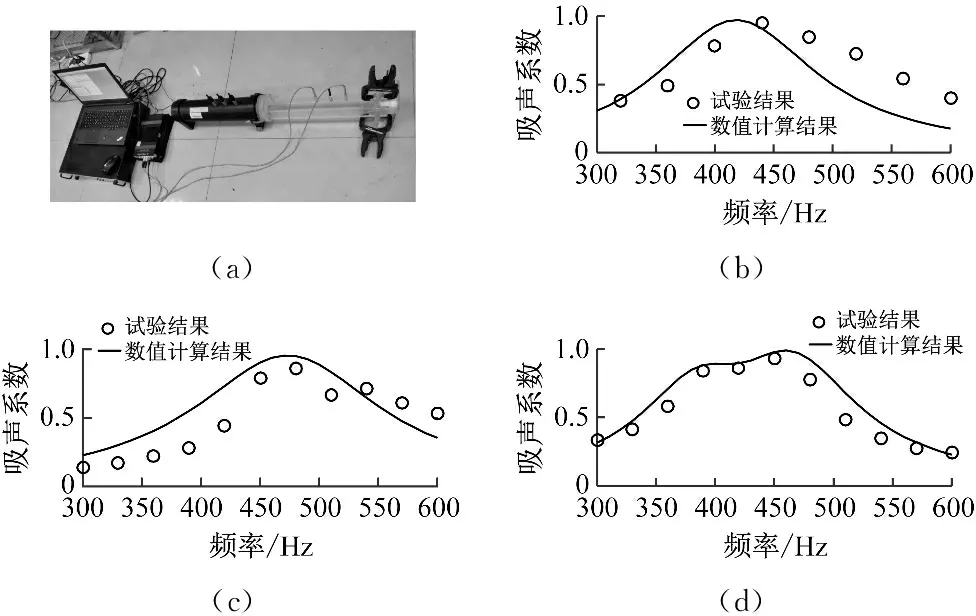
图6 试验装置与试验吸声系数的频响曲线Fig.6 The experimental setup and the experimental absorption coefficient curve

5 结 论

本文在卷曲通道型吸声材料的基础上，引入微缝这一声学原件，设计了一种微缝卷曲耦合低频吸声超材料，建立了其耦合吸声理论模型和数值模型。通过理论模型与数值模型分析得到该吸声超材料能在420 Hz处实现近完美吸声，吸声峰值为0.97，吸声带宽为36.8%，此时结构总厚度为27 mm，仅为共振频率下对应波长的1/30，展现出了良好的低频吸声特性与亚波长尺度特性，此外，缝宽的减小能增加结构的吸声系数与带宽。本文试验结果与数值计算结果匹配良好，证明了该吸声结构的准确性与可行性，同时也将结构的吸声带宽拓宽至49%。综上所述，本文所设计的微缝卷曲耦合低频吸声超材料因其具有良好的低频吸声性能，在噪声控制工程领域中具有应用前景。