基于混合鲸鱼退火算法和稀疏正则化的结构损伤识别

吕 昊， 冯仲仁， 王雄江， 周 伟， 陈百奔

(1.武汉理工大学 土木工程与建筑学院，武汉 430070；2.中建三局集团有限公司，武汉 430064)

工程结构的安全问题一直是众多研究人员的关注热点，有效的损伤识别方法可以准确反映结构的损伤情况，从而降低风险，保障安全[1]。在数学角度上，结构的损伤识别问题可归结为函数优化问题，即通过寻找函数最优值得到对应结构参数，并根据其变化情况对损伤进行识别。随着智能算法日趋成熟，利用智能优化算法进行结构损伤，已取得了显著成果[2]。鲸鱼优化算法(whale optimization algorithm, WOA)是一种由学者Mirjalili在2016年提出的新型智能算法[3]，通过模拟座头鲸的觅食行为实现函数寻优。因其具有调整参数较少，数学结构简单等优点，已在大规模优化[4]、机械故障诊断[5-6]、模型预测[7]等领域得到广泛应用。与其他典型算法类似，WOA同样存在易陷入局部最优和收敛速度慢的问题[8]。

本文首先介绍了WOA的基本原理，数学模型和实现流程，并引入了非线性收敛因子、自适应权重和模拟退火策略对原始算法进行改进，提高算法性能。构建了基于结构模态参数的识别因子，首先阐述了向损伤识别因子中引入稀疏约束的优越性，最后利用ASCE Benchmark结构模型损伤识别数值模拟验证混合鲸鱼退火算法的有效性和抗噪性。

1 鲸鱼优化算法

鲸鱼优化算法是一种新的仿生智能优化算法。该算法模拟了座头鲸的觅食行为，并具有结构简便，调节参数少等优势。在WOA中，假设当前群体中的最优位置为猎物，群体中其他鲸鱼个体均向最优个体包围，并按照优化规则更新位置，直到满足结束条件。整个觅食过程可分为包围猎物、发泡攻击和随机搜索三个阶段。

1.1 包围猎物

由于并无关于全局最优解的猎物位置的先验知识，在鲸鱼优化算法中，假设当前群体中的最优位置为猎物，群体中其他鲸鱼个体均向最优个体包围，并按照优化规则更新位置，其数学表达式为

D=|C·X*(t)-X(t)|

(1)

X(t+1)=X*(t)-A·D

(2)

式中：t为当前迭代次数；X*为当前获得的猎物位置向量；X为鲸鱼位置向量；A和C为系数向量，由下式进行定义

A=2a·r1-a

(3)

C=2·r2

(4)

式中，a为收敛因子，随迭代次数增加从2线性减小到0；r1和r2为[0,1]之间的随机数。

1.2 发泡攻击

在捕食过程中，座头鲸沿螺旋路径逼近猎物，并同时吐出气泡进行攻击。为了模拟座头鲸的这一行为，相应地建立了两种数学模型。

1.2.1 收缩包围

收缩包围机制体现出算法的局部搜索能力，通过降低a值得到实现。由式(3)可见，A的范围随a相应变化，在a由2线性递减至0时，A的取值为[-a,a]；若A在[-1,1]范围内，则更新位置后的鲸鱼将被限定在当前位置与猎物位置之间，从而实现对猎物的包围。

1.2.2 螺旋更新

模拟螺旋更新位置过程，需要首先计算各鲸鱼与猎物之间的距离，并以螺旋式数学模型对鲸鱼的移动方式进行模拟，建模如下

X(t+1)=D′·ebl·cos 2πl+X*(t)

(5)

式中：D′为个体与当前最优位置之间的距离，b为对数螺旋形状常数,取1；l是[-1,1]上的随机数。值得注意的是，上述两种行为是同步进行的，因此在算法中假设鲸鱼选择两种策略的概率均为0.5。

1.3 随机搜索

与收缩包围机制相反，座头鲸需要随机搜索猎物，若A超出[-1,1]范围，鲸鱼将远离当前最优个体，并根据彼此个体位置来更新自身位置，从而一定程度上提高算法的全局搜索性能，数学模型如下

D=|C·Xrand-X|

(6)

X(t+1)=Xrand-A·D

(7)

式中,Xrand为从当前群体中选择某一随机个体的位置。

2 混合鲸鱼退火算法

WOA的调节参数较少，结构简便，具有一定优势，但无法调节收敛速度，即在寻优过程中容易产生早熟；同时，虽然WOA通过随机搜索机制提高全局寻优能力，但针对多峰函数容易陷入局部极值，无法获取全局最优。对此，本文引入非线性收敛因子、自适应权重和模拟退火策略提升算法的寻优性能：首先根据迭代进程，通过非线性收敛因子调整收敛速度；其次，根据自适应权重，提高种群更新机制的多样性，扩大参数空间内的探索范围；最后引入模拟退火策略，以一定概率接受较差位置，从而提高算法跳出局部最优解的能力，提高算法的全局寻优精度。

2.1 非线性收敛因子

原始鲸鱼优化算法通过收敛因子a的变化对全局探索和局部寻优的能力予以平衡。在运行初期，相对较大的a使得算法具有较好的全局搜索能力，避免早熟；在运行后期，相对较小的a则提高了算法的局部寻优能力，加快收敛。但在WOA中，a的递减策略为随迭代次数线性递减，这一策略导致了收敛速度慢、易陷入局部最优等问题，难以完全体现实际搜索过程。实际上在算法运行时，理想的收敛因子在前期保证算法同时具有较好的全局搜索性能和较快的收敛速度，在后期保证具有较快收敛速度，同时避免陷入局部收敛。鉴于此，本文引入了基于二次函数和余弦函数的两段式非线性收敛因子，并定义为

(8)

式中:aini,aend分别为收敛因子的初值和终值;iter为当前迭代次数，itermax为最大迭代次数。

2.2 自适应权重

为平衡算法的全局搜索和局部寻优能力，本文引入了一种加在头鲸上的动态自适应权重，可以根据个体的适应度及其在整个群体的相对位置自适应地对其位置进行更新。具体的操作方法如下：首先将鲸鱼个体根据其适应度函数值进行升序排序，然后对其前后两部分求均值，分别得到Ma1和Ma2，随后根据当前鲸鱼的相对位置，对其赋予权重。

若鲸鱼个体的适应度f(i)小于Ma1，说明该个体为种群中的较优群体，因此设置较小的权重，主要加强其局部细致搜索的能力；

若鲸鱼个体的适应度f(i)介于Ma1与Ma2之间，说明该个体为种群中的一般群体，取权重为1，按算法机制继续向最优位置靠近即可；

若鲸鱼个体的适应度f(i)大于Ma2，说明该个体为种群中的较差群体，需要加强其全局探索能力，按50%概率选择较大或较小权重，从而尽快跳出局部最优。

通过根据适应度调整权重，能加强算法寻优过程中种群个体的多样性，不仅能有效缩减搜索空间，更有利于改善算法的收敛精度和速度。依上述策略，权重w的具体设置如下

(9)

式中：f(i)为第i头鲸鱼的适应度值;k为[0,1]范围内的随机数;w1,w2,w3,w4为自适应权重的限值，并且w4>w3>w2>w1。利用上述自适应权重，将式(2)、(5)改进为

(10)

式中,p为[0,1]范围内的随机数。

2.3 模拟退火策略

模拟退火策略[9]基于固体物质的退火过程与组合优化问题间的相似性，通过以一定概率接受恶化解，从而一定程度避免陷入局部最优。作为模拟退火策略的核心步骤，Metropolis判别准则定义了物体在温度T时状态转化过程中的内能概率，并依次对新解和当前解进行对比，接受较优解的同时，以一定概率接受较差解。本文中将模拟退火策略引入鲸鱼优化算法，降低算法早熟概率。其表达式为

(11)

2.4 混合鲸鱼退火算法步骤

综合上述策略提出的混合鲸鱼退火算法(HWSA)实现结构损伤识别的具体步骤如下。

步骤1 初始化算法参数。包括鲸群数量N，目标维度dim，最大迭代次数itermax，权重因子w1,w2,w3,w4及退火初始温度t0。

步骤2 根据当前迭代进程，利用式(8)计算得到本次迭代的非线性收敛因子a；计算各鲸鱼个体的适应度值，记录当前最优解；对种群进行排序，获取种群均值Ma1和Ma2，利用式(9)计算得到各鲸鱼的自适应权重w。

步骤3 根据p和A的大小更新种群位置。若A≥1，根据式(7)以一随机个体Xrand为基准更新当前位置，否则，通过式(10)相应更新鲸鱼个体位置。

步骤4 模拟退火阶段。定义一个新种群，计算新种群适应度值并与原种群进行对比，通过式(11)进行判别。若新种群优于原种群，则直接替代其位置，反之则以概率P接受新种群。

步骤5 温度冷却过程：t=0.99*t。

步骤6 判断是否达到收敛条件或最大迭代次数，若是，则结束循环输出全局最优解，否则返回步骤2开始新一轮迭代。

3 损伤识别因子

3.1 模态参数识别因子

一般情况下，结构损伤仅引起相应位置的刚度减小[10]，而质量保持不变，则结构的整体刚度矩阵可表示为可表示为

(12)

式中：η为结构损伤因子向量，ηi即第个单元的损伤程度，损伤程度为0时单元健康，为1时彻底失效。Nele为单元个数，Ki为整体坐标系下第个单元刚度矩阵，K(η)即损伤情况η下的整体刚度矩阵。本文选取结构固有频率和振型作为特征构建损伤识别因子。分别表示为

(13)

(14)

式中:N表示选取的模态阶数;ωti和ωei分别表示第i阶频率的理论值和试验值;φti和φei分别表示第i阶频率的理论值和试验值;MAC(φti,φei)为表示模态置信准则。其具体公式为

(15)

利用上述因子即可构建综合识别因子E，并根据其敏感度，对每个因子赋予不同加权系数Δ1和Δ2以缩小数值差异。其计算方法如下

(16)

Δ2=1-Δ1

E=Δ1Eω+Δ2Eφ

(17)

式中：Eω(η)ij和Eφ(η)ij分别表示第j个单元在损伤级别为i时Eω和Eφ的数值;Ndam表示损伤分级数。本文选择损伤分级为10级，即单元损伤程度由轻到重依次为{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}。

3.2 考虑稀疏约束的识别因子

鉴于结构损伤通常仅发生在局部，具有空间稀疏性，为提高损伤识别精度，减少误判单元出现，在式(17)的基础上，引入了Lp范数稀疏约束，即改写为

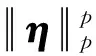
(18)

4 数值模拟

4.1 损伤识别

ASCE Benchmark模型建于加拿大UBC地震工程研究实验室[12]，试验结构为一4层、2×2框钢框架模型，层高0.9 m，每层有8根钢筋斜撑，与梁柱铰接。其物理参数如表1所示。基于MATLAB2019b平台建立了结构的有限元模型，其中，1～32号单元为斜撑单元，33～48号为楼板单元，49～84号为柱单元，单元编号如图1所示。为了研究结构的损伤识别，UBC实验室针对Benchmark模型定义了不同损伤工况，主要通过改变刚度对损伤进行模拟。参考其设置方法，本文设置了6种损伤工况，分别模拟了框架中斜撑的不同程度损伤，如表2所示。研究过程中，将测点布置在各层中间节点，每层布置四个，共计16个测点。提取结构x、y方向的前8阶固有频率和模态振型，用于结构损伤识别。

表1 ASCE Benchmark模型的物理参数Tab.1 Physical parameters of the ASCE Benchmark model

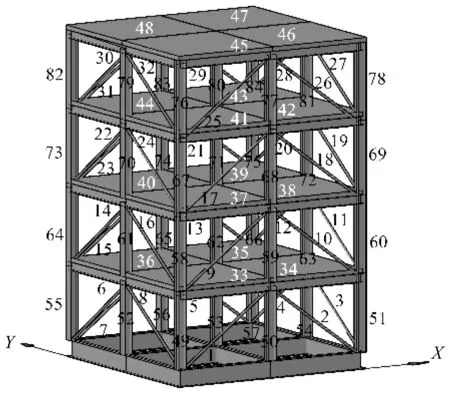
图1 ASCE Benchmark框架结构模型Fig.1 ASCE Benchmark framework structure model

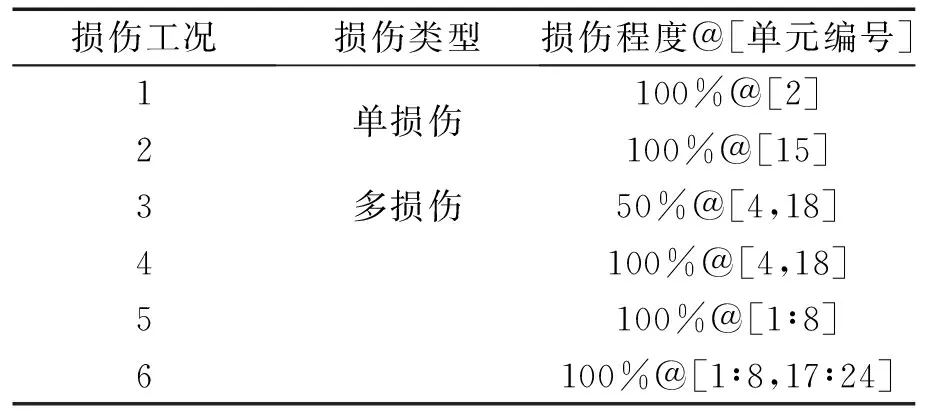
表2 ASCE Benchmark模型损伤工况Tab.2 Damage condition of ASCE Benchmark model

无损状态及各损伤工况下的结构自振频率如表3所示。数值模拟过程中，HWSA初始参数设置为：种群数量N=50，最大迭代次数itermax=100，变量维度dim=84，初始温度t0=0.1 ℃，损伤程度变化范围为[0,1]，各工况均重复计算10次，取最优值作为最终识别结果。

图2为HWSA和WOA的迭代收敛曲线。可以看出，WOA在迭代30次左右后即陷入早熟，且无法跳出局部最优，导致全局寻优效果不佳，HWSA则进行了更广泛的全局探索，同时始终保持了跳出局部最优的能力，并在运行80次后收敛。值得注意的是，HWSA的目标函数最终收敛值比WOA小两个数量级，可以认为HWSA的寻优性能相比WOA有了较大提高，说明本文提出的改进措施是可行有效的。

针对在识别因子中引入稀疏约束的可行性进行讨论，利用HWSA对前四种工况分别进行损伤识别，当识别结果中单元损伤程度大于5%时即视为单元损伤，否则视为处于无损状态，考虑不同稀疏约束的识别结果如表4所示。从表中可以看出，不考虑稀疏约束时，识别结果中非零单元个数较多且出现误判，影响损伤识别精度和准确性；当考虑稀疏约束时，识别结果更趋于真实值，且非零个数明显减少，说明稀疏约束的确在损伤识别过程中起到了积极作用。其中考虑L0.5稀疏约束时，识别结果中的非零单元个数与实际损伤个数相同，具有较好的稀疏性，说明L0.5有效改善了原有问题的病态性，从而提高了结构损伤识别精度；当考虑L1稀疏约束时，虽然损伤位置处的识别结果相对较好，同时非零元素个数明显减少，但识别误差较大，导致工况3的22号单元被误判为损伤；当考虑L2稀疏约束时，与未添加稀疏约束相比，识别精度提升不大，非零单元个数有所减少但误差明显，导致工况4的10号单元被误判为损伤。综上，L1或L2稀疏约束所提供的约束不足，在描述真实损伤的稀疏性时作用有限，导致优化算法无法获取全局最优解，而L0.5稀疏约束对结构损伤识别精度的提升效果最佳，因此后续研究均采用考虑L0.5稀疏约束的识别因子进行损伤识别。

表3 不同工况下结构的自振频率Tab.3 Natural frequencies under different working conditions Hz

图2 HWSA和WOA迭代收敛图Fig.2 Iterative convergence graph of HWSA and WOA

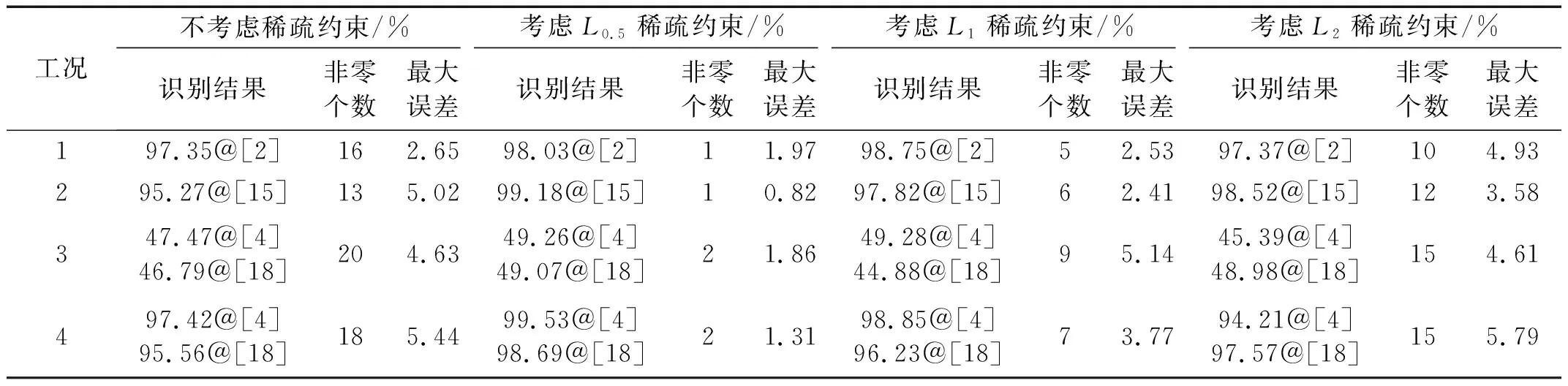
表4 不同稀疏约束在结构损伤识别中的影响Tab.4 The influence of different sparse constraints on structural damage identification

4.2 结果分析

分别采用WOA、HWSA和PSO进行了6种工况的损伤识别，三种优化算法的识别结果如图3所示。由于文中仅定义了与斜撑相关的损伤工况，并未涉及柱、板单元的损伤，因此仅展示斜撑单元的识别结果对比。可以看出：

(1) 对于工况1和工况2，HWSA均能较准确地识别损伤位置和程度，未对无损单元造成误判；WOA能较好地识别实际损伤位置及程度，但存在误差，在工况2 中11号识别结果为8.59%，被误判为损伤；PSO对损伤位置的识别较好，但损伤程度的识别精度较差，在工况2中15号单元的识别误差达到20.65%，同时11号单元识别结果为8.74%，造成误判。

(2) 对于工况3和工况4，HWSA的识别结果比较准确，趋近真实损伤情况，且未出现误判；WOA对于损伤位置的识别较好，对损伤程度的识别存在误差，在实际损伤处的最大识别误差为9.61%，在无损单元处的最大识别误差为8.33%，导致产生误判；PSO的识别结果存在一定偏差，不仅在实际损伤位置处的损伤程度识别误差较大，同时造成工况3中的7号、26号单元和工况4中的3号单元被误判损伤。

(3) 对于工况5和工况6，HWSA仍能较准确地识别实际损伤；WOA的识别效果较好，但在工况5中1号单元处识别结果为91.91%，明显小于实际损伤程度，且在无损单元处出现了非零的识别结果，但均较小，仍可视作健康状态，不影响对结构状态的判断；PSO损伤位置的识别较好，但对于损伤程度的识别结果不够理想，在工况5中1号单元处的识别结果仅为83.01%，同时非零单元个数增多，但未造成误判。

识别结果中的误判单元基本出现在实际损伤的同层同轴或异层同轴平面内，主要原因是识别因子的主要组分是结构的模态参数。结合所有工况的识别结果及对比可以看出，HWSA的识别效果最优，WOA次之，PSO最不理想。HWSA可以满足结构损伤识别的精度要求，可有效且准确地识别结构损伤位置和损伤程度。

4.3 抗噪性分析

针对HWSA的抗噪性进行进一步探究，考察不同程度噪声水平对于模态参量的影响，同时对频率和振型添加噪声，加噪公式为

pn=pp(1+LnMn)

(19)

式中：pn和pp分别为含噪和不含噪的模态参量；Ln表示噪声水平，本文中Ln取{1%,5%}；Mn为一随机矩阵，表示该矩阵内各元素均为[0,1]范围内的随机数。

利用HWSA对上述工况在不同噪声水平下进行损伤识别，识别结果如图4所示。

可以看出：添加噪声后，在实际损伤处的识别结果与无噪环境下差别不大，均趋近真实值，说明本文方法在噪声环境下性能稳定，能准确识别结构的真实损伤；随噪声水平增加，无损单元处的非零识别结果增多，但数值均较小，仍可视为无损状态，不影响实际损伤的识别，说明本文方法具有一定的抗噪性。

5 结 论

本文提出一种基于混合鲸鱼退火算法和稀疏正则化的结构损伤识别方法。该方法改善原始鲸鱼优化算法性能并结合稀疏约束，应用于结构损伤识别，最后通过ASCE Benchmark结构模型验证其有效性和适用性。结论如下：

(1) 目标函数的收敛曲线和收敛值表明，引入改进策略后，混合鲸鱼退火算法的寻优性能优于原始算法，早熟现象得到显著改善；

(2) 稀疏约束有利于损伤结果的稀疏表示，能减少误判并提高识别精度。其中L0.5约束对识别精度提升最为显著；

(3) 在ASCE Benchmark各损伤工况下，本文方法的寻优精度均优于其他方法，说明了本文方法的有效性和可行性；

(4) 在噪声环境下，本文方法性能保持稳定，损伤识别效果较好；随噪声增加，无损单元处出现非零结果，但不影响损伤判断，说明本文方法具有一定的抗噪性。