基于VC的测绘坐标转换程序设计与实现

陈晓楠，唐晓艳，杨非凡，孔鲁宁，陈贞竹

（新疆大学建筑工程学院，新疆乌鲁木齐，830047）

1 坐标系及我国常用坐标系统介绍

1.1 坐标系分类介绍

（1）地心坐标系统是以地球质心为坐标系原点的坐标系统。地心坐标系的建立需要先确定地球椭球体、定位和定向以及确定尺度。它是以地球质心为原点，Z 轴与国际协议地极CIP 极轴相重合，起始子午面与BIH 平子午面相重合。地心坐标系是一个总称，可以具体分为地心直角坐标系（X、Y、Z）和地心大地坐标系（B、L、H）。这两种形式的坐标系可以相互换算。

（2）参心坐标系是以参考椭球的中心为坐标原点的坐标系称为参心坐标系。参心坐标系的建立需要先建立大地原点，选择椭球的长半轴a 和扁率α，即确定椭球的几何参数，确定椭球的中心位置及确定椭球的坐标轴指向。该坐标系最大的特点就是它与参考椭球的密切联系，即可以分为空间直角坐标系和大地坐标系两种。空间直角坐标系的原点位于椭球中心O（地球质心），Z 轴与短半径重合，指向北，X 指向经度零点，Y 轴垂直于XOZ 平面并与X、Z 构成右手坐标系。

（3）站心坐标系是用于了解以观察者为中心的以外物体的运动规律，通常以测站点的位置为坐标原点，建立起以测站点为参考的空间位置关系。它的服务范围小，用于某一地区的工程测量建设。因为距离近，站心坐标系可以对周围事物进行精密定位。

1.2 我国常用坐标系统介绍

（1）1954 北京坐标系统

20 世纪50年代，在我国天文大地网建立初期，为了社会主义经济建设和国防建设，发展我国的测绘事业，需要建立一个参心大地坐标系统，为此我国以1942年苏联普尔科沃坐标系为基础，经过东北边境的呼玛、吉拉林和东宁三个基线网，同前苏联的大地网联接，这样的坐标系统定名为1954 北京坐标系统。

（2）1980 西安大地坐标系系统

为了适应我国经济及大地发展的需要，我国重新对全国天文大地网实行整体平差，并建立了1980 西安大地坐标系统。大地原点位于我国中部——西安市以北60km 处的泾阳县永乐镇，简称西安原点。该坐标系采用1975年大地测量与物理联合会第16 届大会推荐的4 个基本椭球参数、1956年黄海高程基准，是在1954年北京坐标系基础上建立起来的。

（3）WGS-84 坐标系

1984年世界大地坐标系（WGS-84）是美国依据TRANSIT 卫星定位测量数据建立的协议地球坐标系统，是目前GPS 所采用的坐标系统。它是一个地心地固坐标系统，坐标原点位于地球的质心。Z 轴指向BIH1984.0 定义的协议地球极方向，X 轴指向BIH1984.0 的起始子午面和赤道的交点，Y 轴与X 轴和Z 轴构成右手坐标系。WGS-84 坐标系统是现有的应用于航海图、测绘地图、大地测量和导航最好的全球大地参考系统。

（4）2000 国家大地坐标系

2000 国家大地坐标系是我国当前最新的国家大地坐标系统，是右手地固正交坐标系。它的坐标原点为包括海洋和大气的整个地球的质量中心，Z 轴指向历元2000.0 的地球参考极的方向，X 轴指向格林尼治参考子午线与地球赤道面的交点，Y 轴与X 轴和Z 轴构成右手正交坐标系。2000 国家大地坐标系满足了我国国防建设、经济建设、社会发展、科学研究及社会进步的新要求，有利于提高大地控制点的三维坐标精度，加快测绘人员的工作效率。

2 坐标转换系统数学模型介绍

2.1 空间直角坐标与大地坐标之间的转换

(1)大地坐标（B,L,H）转换为空间直角坐标（X,Y,Z）

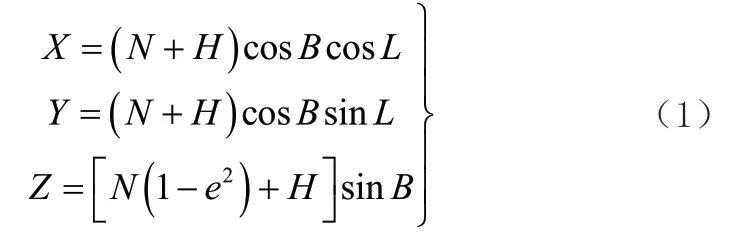
式中，B、L、H 为椭球面上的大地纬度、大地经度、大地高，X、Y、Z 为空间直角坐标。e2为第一偏心率平方，N 为卯酉圈曲率半径，

(2)空间直角坐标（X,Y,Z）转换为大地坐标（B,L,H）

式中，大地经度L 可根据X、Y 直接进行计算。大地高H 和大地纬度B 需要进行迭代计算。一直到Bi−Bi−1和H i−Hi−1小于所要求的限值，则停止迭代。

2.2 高斯平面坐标与大地坐标之间的转换

(1)大地坐标（B,L）转换为高斯平面坐标（X,Y）高斯投影正算的公式为：

其中： L 为经度值，B 为纬度值，N 为卯酉圈曲率半径，l是待算点相对于中央子午线的经度差，L0是中央子午线经度值，e 为地球第二偏心率。

(2)高斯平面坐标（X,Y）转换为大地坐标（B,L）

高斯反算的公式为：

3 坐标系统转换基本模型介绍

若坐标系统建立在不同的椭球基础上，则需要用不同地球椭球基准下的空间直角坐标系点位坐标转换。共需要采用7 个参数，是3 个旋转参数ωX、ω Y、ωZ，3 个平移参数dX0、dY0、dZ0，1 个尺度变化参数m。

3.1 布尔沙模型

假设有两个空间直角坐标系O−XYZ和O'−X'Y'Z'，这两个坐标系的原点不同，则存在平移参数，且各坐标轴之间相互不平行，则存在旋转参数。两个坐标系的尺度不相同，则形成尺度变化参数。则任一点Pi在两个坐标系中的坐标之间的关系为：

上式称为布尔沙模型，简称为B 模型。

3.2 莫洛琴斯模型

莫洛琴斯模型在建立坐标系时，两个坐标系的轴向是一致的，即两个空间直角坐标系的三个轴线相互平行，只是任意一点Pi和另一个参考点的坐标之差，数学模型如下：

上式为莫洛琴斯模型，简称M 模型。

4 坐标系统转换的实现

4.1 功能介绍

本坐标转换系统能够实现大地坐标与平面直角坐标、大地坐标与空间直角坐标、平面直角坐标与空间直角坐标之间的相互转换。

4.2 界面设计

是本程序设计的运行界面，根据所转换的坐标系将主页面分为三个部分，输入已知坐标及中央子午线经度再点击转换按钮，则其余两个目标坐标将得以转换。

4.3 算例解算

以大地坐标转换为空间直角坐标及平面直角坐标为例：已知WGS-84 坐标系下的大地坐标，用本程序计算的空间直角坐标和平面直角坐标。

5 结语

本文总结了空间直角坐标系、大地坐标系、平面直角坐标系之间的数学模型及转换过程，对坐标系转换的基本模型即布尔沙模型和莫洛琴斯模型进行了基本介绍，并将两者结合，得出转换方法。结合已经编出的程序，将坐标点代入，验证转换结果。结果发现，基于VC++所设计的程序语言简单，没有运用过于复杂的运算方式，运行流畅且无数据丢失情况，输出的数据也与真实值偏差较小。所以可以得出，该程序无数据稳定性及数据安全方面的问题。

设计界面虽然简单明了，但是不够美观。在论文过程中，只是对于小部分的数据进行转换，没有采用大量数据，所以程序的稳定性有待于研究。同时所使用的椭球参数较少，在今后的研究中需加入更多参数，以便更加完善研究成果。