一种适用于建材检测实验室测量不确定度的通用评定方法

杨俊杰

（珠海市金湾区建设工程质量监测站，广东珠海 519041）

一切测量结果都具有不确定度。不论是CMA 资质认定还是CNAS 能力认可评审，都要求检验检测机构具备对每一项检测参数数值进行测量不确定度评定的能力。在实际工作中，当检测结果与标准要求限制非常接近时，在不给出不确定度的情况下，直接依照检测结果进行结论判定往往会承担巨大的误判风险。当前，对不确定度的研究已比较成熟，已有相关标准对不确定度进行规范化流程指引。而在实际工作中，尤其是在建材检测领域，由于各实验室能力参差不齐，检测人员素质高低有别，不确定度评定这项工作往往未能被正确对待。通过提炼总结建材检测的特点，梳理出一种简化过的、具有普遍适用性的不确定评定流程，可为建材实验室的不确定度评定工作提供借鉴，从而大大降低不确定度评定工作难度，提升实验室测量不确定度评定工作的整体水平。

1 建材实验室测量方法特点

建设工程领域建材检测实验室主要为建设工程材料进场验收提供第三方检测服务，按照样品特点，试验可主要分为可重复试验的非破坏性检验和单个样品无法重复测量的破坏性检验。建材检测往往单一检测方法较简单，但样品种类和检测参数繁多，对每个检测结果逐一进行不确定度评定难度较大。检测机构常常因为评定过程烦琐，而忽略了测量不确定的评定工作。

在本单位建材检测项目的不确定评定过程中，对不确定主要贡献进行统计分析时，发现不确定度贡献最大的为重复测量所计算所得的系统误差。因此，设计一个好的重复试验可将检测模型简化为几个基本分量。在此基础上，提出一种通用简化的测量不确定度评定方法，可大大降低不确定度评定工作难度，提高可操作性。

2 测量数学模型的建立

在建材检测中，常见的测量物理量为载荷、尺寸、质量、温度等，这些测量数据基本都能通过直接读数所得，且不相关。某一项检测参数的结果，为上述基本物理量实测数据经过公式计算而来，如强度等于载荷除以受力面积等。用公式表达可为：

在实际应用中，根据检测项目确定具体计算公式，公式中有多少直接测得的物理量，即可认为有多少个不确定度的分量。

3 各分量不确定度的评定

3.1 合理设计独立重复试验

考虑不同因素对各分量不确定度的影响，一般从人员操作、设备准确度和重复性、样品的均匀程度等方面来考虑。设计包含所有不确定因素的独立重复试验，重复试验次数见表1。每个不确定度分量的独立重复测量总次数以不少于10 次为宜。

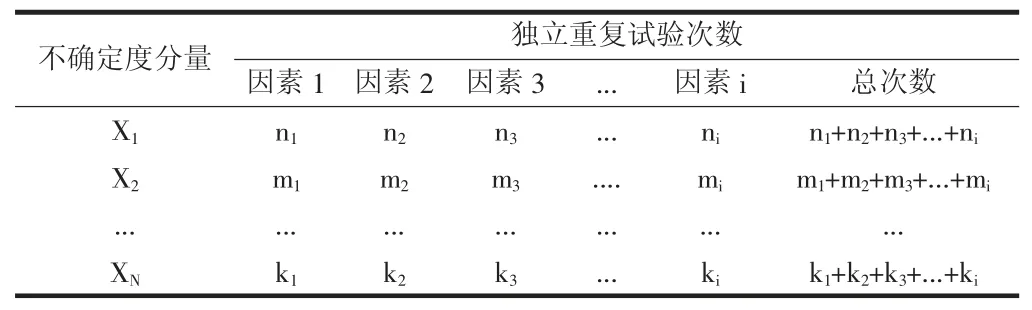
表1 独立重复试验次数分布

3.2 计算各分量重复试验结果的实验标准偏差

根据贝塞尔公式，计算各个分量测得值的试验标准偏差：

式中：xk-单次测量结果；x-重复测量结果的平均值。

在具体检测方法中，若某个分量取值为取m 个检测值的平均值，则该分量的A 类标准不确定度为：

3.3 计算各分量的灵敏系数

对式（1）求导，得：

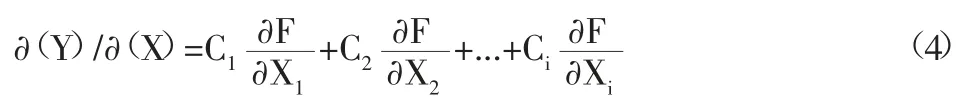
式中：C1-分量X1的灵敏系数；C2-分量X2的灵敏系数，以此类推。

3.4 设备设备引起的B 类不确定度

查阅设备技术资料和校准证书，找出设备准确度，可认为设备示值在准确度范围内均匀波动，服从均匀分布。设其波动半宽为a，由设备引起的不确定度可统一表示为：

4 合成不确定度

将各分量合成，按式（6）进行计算

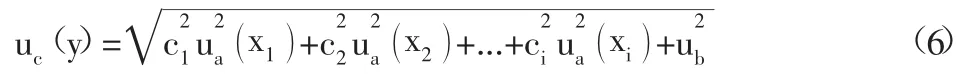
5 结果表达

测量不确定的结果宜表示为扩展不确定度，扩展不确定度由合成标准不确定乘以包含因子所得，包含因子一般取值为k=2。

因此，最终不确定度可以表示为U=k·UC，k=2。

不确定计算时，结果修约应与检测数据结果位数保持一致。

6 应用实例（以水泥三天抗压强度为例）

6.1 试验方法

水泥强度检验采用《水泥胶砂强度检验方法（ISO 法）》（GB/T 17671—1999）进行检验。准确称取450g 水泥样品，与1350g 标准砂和225g 水混合，搅拌后装入试模成型，振实后在20±1℃，相对湿度不大于90%的养护箱养护24h 后脱模，随后放入20±1℃的水中养护至规定龄期。取出后，在压力试验机上使用专用夹具进行强度试验。

6.2 测量数学模型及不确定度来源分析

强度公式：RC=FC/A，FC-极限载荷；A-受压部分面积。

根据强度公式可知，强度与极限载荷和受压部分面积有关，而在水泥3d 抗压试验时，受压部分面积取固定值40×40=16000mm2，因此A 可看做是常数。其抗压强度值主要受极限载荷单一因素影响，因此测量数学模型可进一步简化为：Y=X。

6.3 重复试验

进一步分析可知，不同操作人员操作习惯，不同设备的计量特性可能会对试验结果产生影响。本单位实验室在日常检测中，有两台抗压设备随机选用，有3 名检测人员随机取用样品进行检测，在设计重复试验时，尽量能还原日常检测过程，以充分考虑不同因素产生的影响。

选取了一份约10kg 的水泥样品，经匀质化处理后均分成18份，每名试验员成型6 组抗压强度样品后，分别在两台压力试验机上进行3d 抗压强度试验，每组样品6 个强度数据的平均值作为本组抗压强度值。具体试验数据如表2。

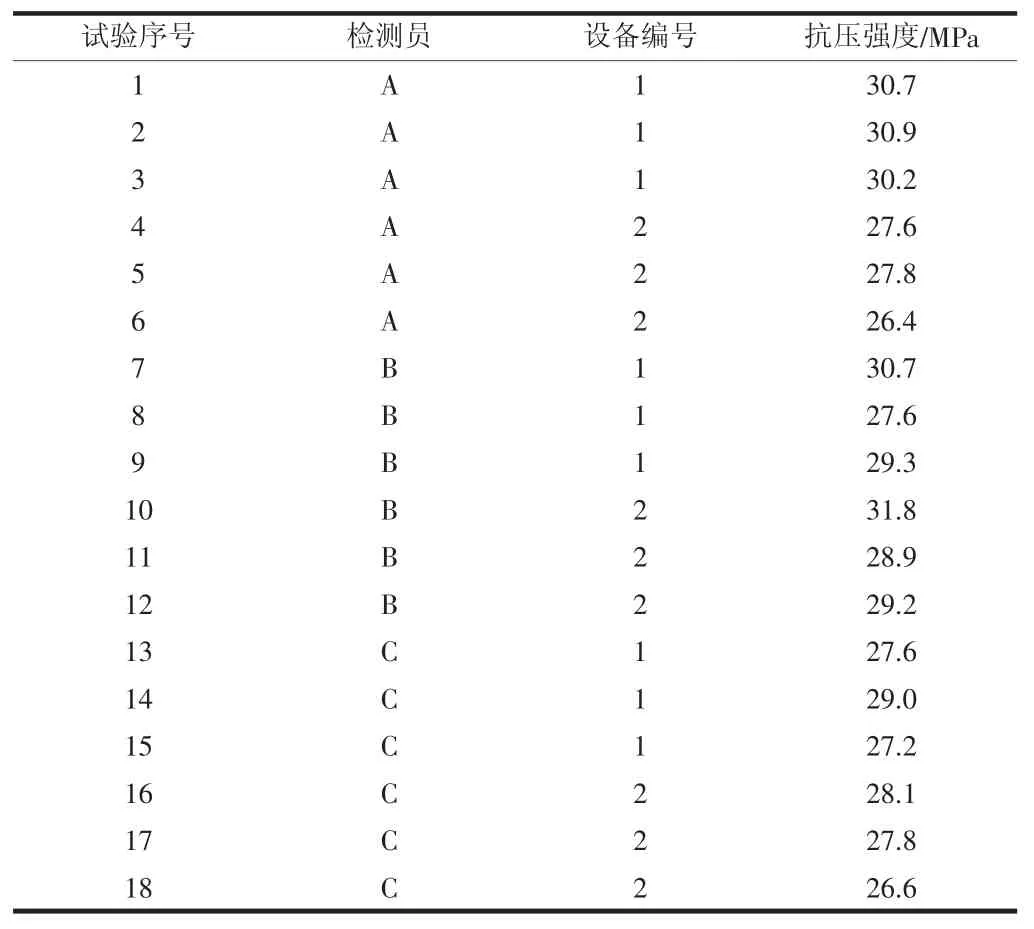
表2 重复试验检测结果汇总

6.4 不确定度计算

利用贝塞尔公式：S（x）=1.6MPa。

由前述分析可知，抗压强度不确定度被简化为仅有随机效应这一个误差，各影响因素已被包含到重复试验中。同时，在进行计算时，直接将6 个平均值作为单次测量结果，因此，A 类标准不确定应为：u（x）=S（x）=1.6MPa。

扩展不确定度为：U=ku=2×1.6=3.2MPa，k=2。

7 结语

本文在总结建材检测实验室不确定评定的基础上，提炼出了一种适用于简单测量模型（通常是物理检测）的不确定度通用评定方法。针对日常不确定度评定中难以确定不确定来源，并难以对各来源进行量化评价的难点，利用合理设计重复试验的方法确定各分量不确定度的具体计算过程。该计算方法的不足之处在于，将检测模型简化为独立不相关的几个直接测得物理量的简单数学运算，对于一些非直接读数（如需要工作曲线准换数据）所得的物理量，其不确定度评定数据精确度大大降低，计算结果往往偏大。在对不确定度评定没有严格的精确度要求的情况下，参考此流程，可大大降低不确定度评定难度，可对实验室检测能力及数据应用，提供有益参考。