基于滑窗滤波和多项式拟合的时变信道估计方法

景兴红，孙国栋，何世彪，廖 勇*

（1.重庆工程学院电子信息学院，重庆 400056；2.重庆大学微电子与通信工程学院，重庆 400044）

（*通信作者电子邮箱liaoy@cqu.edu.cn）

0 引言

随着无线通信技术的广泛应用，结合自动驾驶和信息娱乐等应用的智能交通系统（Intelligent Traffic System，ITS）受到了学术界和工业界的广泛关注。针对车辆通信的高可靠性和低延迟等需求，信号接收侧准确的信道估计是保证通信系统服务质量（Quality of Service，QoS）的必要前提［1-3］。第三代合作伙伴计划长期演进（The 3rd Generation Partnership Project Long Term Evolution，3GPP-LTE）系列标准在最近的版本中对设备到设备（Device-to-Device，D2D）和车辆到一切（Vehicle to Everything，V2X）通信作出了规定，基于长期演进（Long Term Evolution，LTE）的V2X（LTE based V2X，LTE-V2X）标准在中国车载通信行业中被广泛应用。对于V2X 通信场景，车辆的高移动性会产生严重的多普勒频移影响，因此信道估计不仅仅需要抵抗多径效应带来的频率选择性衰落，同时还要能跟踪高速移动下信道的时变特性，这给V2X 信道估计带来了挑战［4-5］。

在LTE-V2X 标准前，车载通信采用专用短程通信（Dedicated Short Range Communication，DSRC）下 的IEEE 802.11p 标 准［6］，该标准采用正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）传输系统，而在物理层帧结构上设置长训练符号来进行信道估计，而在数据符号处，文献［7］采用增强的均衡方案谱时间平均（Spectral Temporal Averaging，STA）方法，通过对数据子载波的信号判决进行信道响应更新，并同时在时域和频域中进行窗口平均提升估计精度。文献［8］中提出了一种基于长训练导频序列的估计信道频域响应（Channel Frequency Response，CFR）和构造数据导频（Constructed Data Pilot，CDP）的信道估计方案，其基本思想也是通过判决反馈来更新CFR，进而跟踪信道变化。LTE-V2X 标准采用单载波频分多址（Single-Carrier Frequency-Division Multiple Access，SC-FDMA）的系统传输方案，由于调制后的数据符号需要进行离散傅里叶变换（Discrete Fourier Transform，DFT），导致频域发送符号会存在接近零的模值，基于数据符号处的判决反馈并利用最小二乘法（Least Squares，LS）估计更新信道响应产生极大的误差，因此判决反馈的信道估计思路并不适用。LTE-V2X 标准［9］沿用了LTE 的帧结构，在一个子帧中插入4 个块状导频用于信道估计。文献［10］提出了一种新的基于导频的信道估计方法，用低阶线性最小均方误差（Linear Minimum Mean Squared Error，LMMSE）估计方法实现导频处的信道估计，并通过DFT运算以提高导频处的估计精度，最后通过插值方法获取数据符号处CFR。文献［11］提出了一个基于LTE 的车对车（Vehicle to Vehicle，V2V）环境下的智能信道估计方案，采用基于导频符号二次平滑的自适应平滑信道估计方案，在数据符号中自适应地跟踪信道变化。在文献［12］中提出了一种基于基扩展模型（Basis Expansion Model，BEM）的时变信道冲激响应（Channel Impulse Response，CIR）估计方法，并利用基于Slepian 序列的分段插值方法重建数据符号的时域信道响应。上述文献中的方法基本都是采用判决反馈和信道插值的方法来跟踪时变信道，判决反馈的信道估计策略随迭代次数提高会极大增加方法的复杂程度，而信道插值又难以达到良好的信道拟合效果。

为了能更准确地跟踪并估计得到不同多普勒频移下的时变信道，本文设计了一种基于滑窗滤波和多项式拟合的时变信道估计方法。一方面，通过滑动窗口平滑处理降低导频处CFR估计的噪声影响；另一方面，采用多项式信道拟合来获取数据符号处的CFR，并根据信道最大多普勒频移的大小，采用不同阶数的拟合多项式跟踪信道变化。通过仿真系统验证，本文方法能适应不同多普勒频移下的时变信道，并有效提升信道估计的归一化均方误差（Normalized Mean Squared Error，NMSE）和系统误比特率（Bit Error Rate，BER）性能。

1 系统模型

SC-FDMA系统的数据处理流程如图1所示。记符号调制后的时域数据符号为d(m)，调制符号经过M点DFT 为频域符号D(k)：

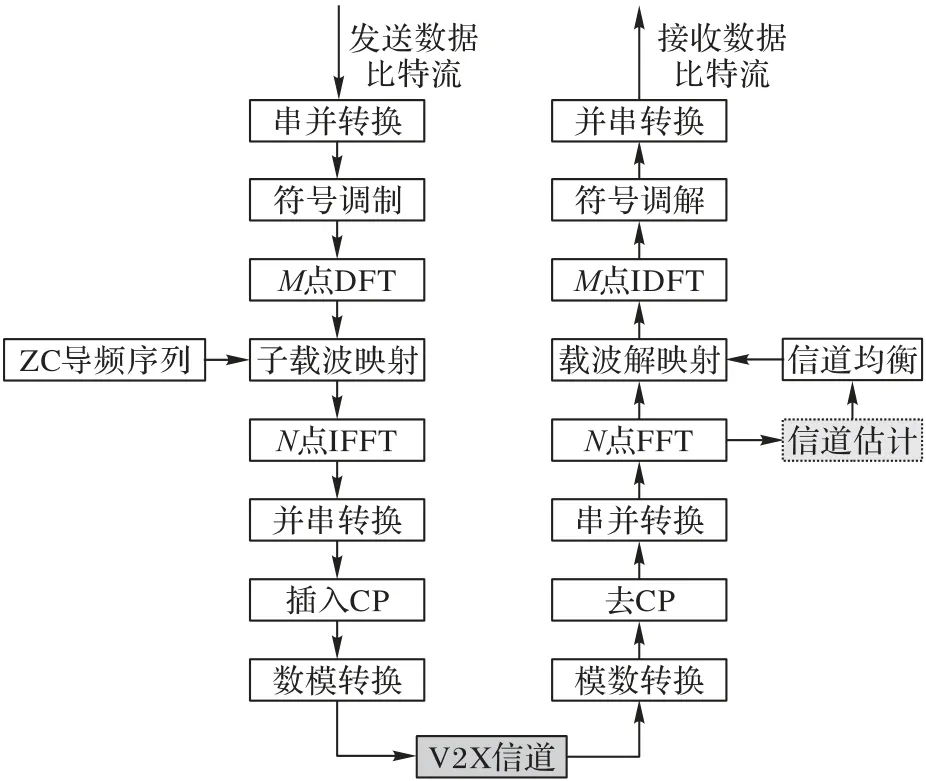
图1 SC-FDMA系统流程Fig.1 Flowchart of SC-FDMA system

接着频域符号D(k)被分配到频域指定的数据传输载波位置，记补零之后的子载波数为N(N>M)，对应频域发送符号S(k)：

其中：k=0，1，…，N-1；λd表示数据子载波的载波位置序列集合；λ0表示零载波的位置序列集合，本文采用集中式载波映射的方式［13］。

在完成数据符号的载波映射后，需要将ZC（Zadoff-Chu）序列［14］以块状导频方式插入子帧，形成完整的频域资源网格。经过N点的快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）后得到时域发送序列x(n)：

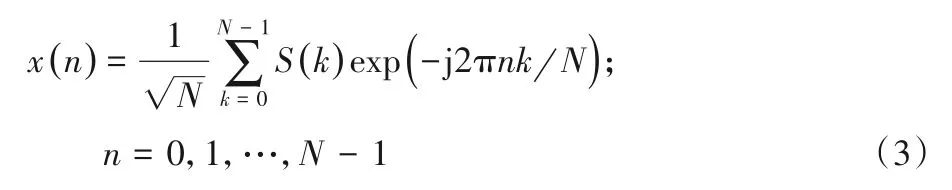
插入循环前缀（Cyclic Prefix，CP）后的发送序列表示为x(n)，其中：n=-Ncp，…，0，1，…，N-1；Ncp为CP 的长度。将发送序列进行数模转换后经无线信道传输至接收机端，无线信道传输过程可以表示为：

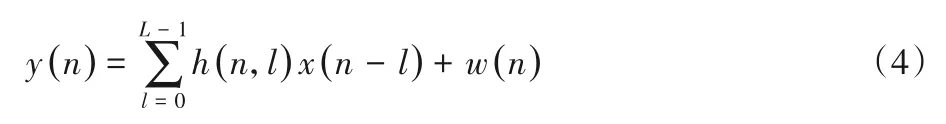
其中：h(n，l)表示第n个采样时刻第l个抽头的信道增益；L表示信道最大抽头时延；w(n)是第n个采样时刻方差为σ2的零均值复加性高斯白噪声。

记Fn，k=为N点傅里叶变换矩阵。因 此，式（3）可以被表示为x=FHS，其中：x=[x(0)，x(1)，…，x(N-1)]T，(⋅)T表示矩阵的转置；S=[S(0)，S(1)，…，S(N-1)]T；(⋅)H表示共轭转置。接收信号经过快速傅里叶变换（Fast Fourier Transform，FFT）得到：

其中：Y=[Y(0)，Y(1)，…，Y(N-1)]T表示接收符号向量y=[y(0)，y(1)，…，y(N-1)]T的傅里叶变换，W=Fw表示复加性高斯白噪声向量w=[w(0)，w(1)，…，w(N-1)]T的傅里叶变换。G∈CN×N为信道冲激响应矩阵，有：

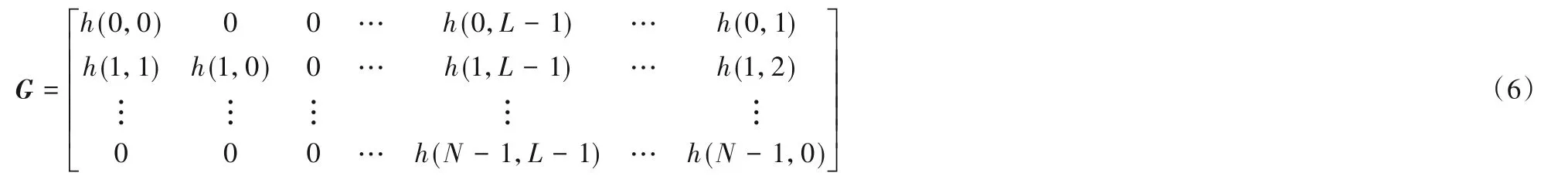
系统频域传输模型可以表示为：

其中：H=FGFH为CFR 矩阵，是信道估计的求解目标。接收机将估计得到的CFR 矩阵用于信道均衡，并完成载波解映射和解调等步骤后即可恢复出数据比特流。

2 信道估计

LTE-V2X 标准沿用LTE-D2D 的物理层传输的帧格式［12］。如图2 所示，一个传输子帧中包含14 个传输符号，其中4 个解调参考信号（Demodulation Reference Signal，DMRS），分别放置在第3、6、9、12 个符号位置，可作为信道估计的导频，第一个和最后一个符号分别用于自动增益控制（Automatic Gain Control，AGC）和保护周期（Guard Period，GP），其余符号作为信息数据传输符号。为方便理解，方法描述中，对传输符号只区分导频符号和数据符号。因此，在可以利用导频符号采用LS 估计得到导频符号处的CFR，而数据符号处的CFR 可以通过信道跟踪来获取。

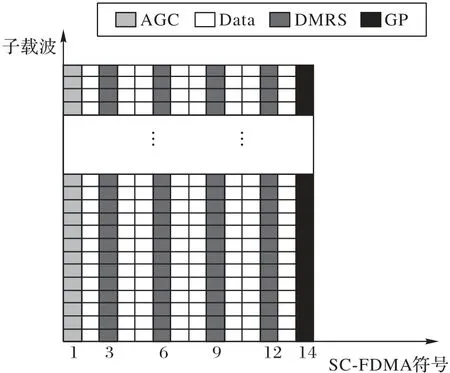
图2 LTE-V2X标准的帧格式Fig.2 Frame format of LTE-V2X standard

2.1 滑动窗口去噪

LS 信道估计方法并没有考虑到信道噪声的影响，在导频处的CFR 估计并不准确。LMMSE 方法可以利用传输信道自相关特性和噪声方差来对LS方法的估计结果进行修正，然而LMMSE 方法需要得到实际信道的自协方差矩阵，在实际通信场景下是无法获取的，因此该方法可以作为基于LS信道估计结果的理想去噪性能上限。

为了能在LS 估计方法基础上降低噪声对导频处CFR 的影响，采用了滑动窗口平均的思想对LS估计结果进行滤波去噪。导频处CFR通过LS估计可以表示为：

其中：SZC(k)表示频域的ZC 导频序列；HLS(k)为LS 估计的导频处CFR；k=0，1，…，N-1。记滑动窗口的长度为Lw，滑动窗口滤波处理过程如下：

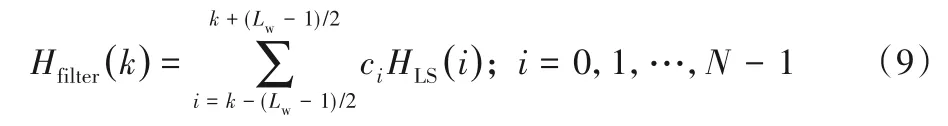
其中：ci表示权重系数，可以取ci=。

滑动窗口长度是滑动窗口滤波方法的一个重要参数。多径效应导致CFR 会有明显的频域选择性衰落，因此滑动窗口长度如果设置很小，信道噪声对滤波结果的权重影响较大，会导致滑动平均的滤波效果变差；但如果窗口长度设置很大，又无法有效地拟合频域选择性衰落的特性。因此，根据仿真实验最后根据传输信道的信噪比（Signal-to-Noise Ratio，SNR）估计［15］来自适应确定滑动窗口长度的大小：

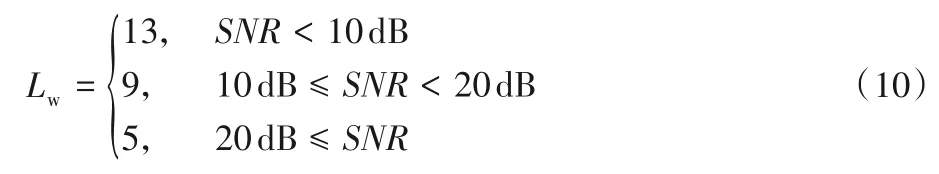
当SNR比较小时，噪声影响较大，因此需要设置较长的滑动窗口大小来达到去噪的目的；而当SNR较大时，LS 方法的估计精度就已经比较高了，此时可以设置较小的窗口长度。

2.2 多项式拟合

在导频处通过滑动窗口滤波的方法降低了噪声的影响，在数据符号处的CFR 通常是采用插值方法进行获取。为了选用更加合适的插值方法，首先需要研究不同传输符号位置处的CFR 的变化情况，其变化的主要影响因素是终端移动导致的多普勒频移大小。当通信终端处于静止或低移动性状态时，多普勒频移较小，导致不同符号处的CFR 变化缓慢，此时采用低阶的线性插值来拟合其变化；反之多普勒频移较大时则需要利用高阶插值进行时变信道拟合。

采用插值方法信道估计最大的问题在于过于依赖导频处的估计效果，如果导频处CFR 估计准确，则通过插值方法获取的数据符号CFR 也比较准确；但是如果导频处CFR 估计由于噪声影响偏差较大，则数据处插值也会收到严重影响。为了能更有效地跟踪一个传输子帧内CFR 的变化，设计了一种阶数自适应应的多项式拟合方法。

记一个子帧中包含T个SC-FDMA 传输符号，其中包含Tp个导频符号和Td个数据符号，则可以利用多项式拟合的方法来跟踪一个子载波的CFR在T个传输符号间的连续变化：

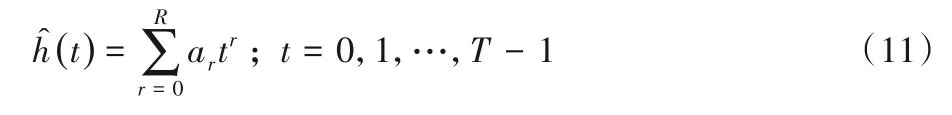
其中：t表示一个子帧内的符号序号；R表示多项式最高阶数；ar是多项式拟合第r阶的系数；(t)表示多项式拟合的不同符号处的CFR。

采用最小化NMSE的思想来计算多项式拟合的系数，NMSE的表达式为：

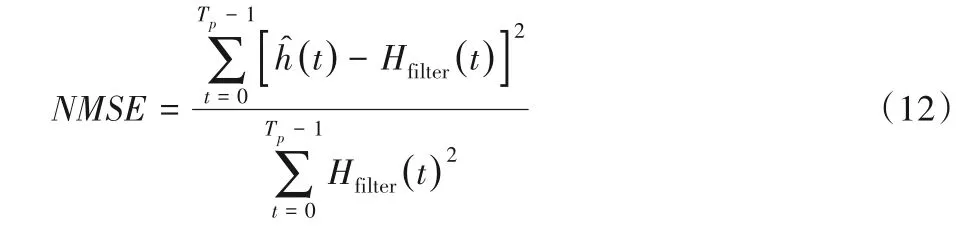
第3、6、9、12 导频符号处的滑动窗口去噪的估计结果为Hfilter(t)，t=3，6，9，12，由此可建立表达式如下：

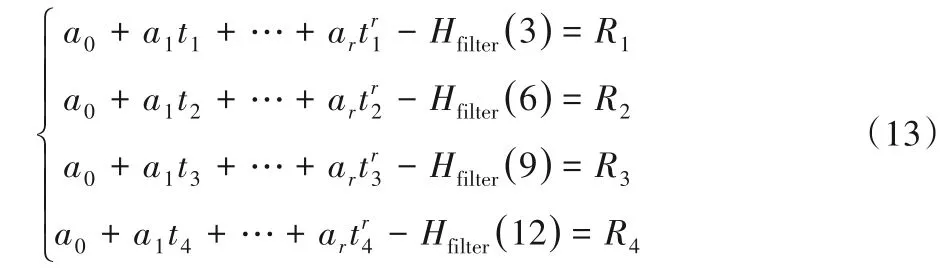
其中：R1～R4表示4 个导频位置的拟合误差。通过LS 使得式（12）的拟合误差达到最小，由此式（13）表示为矩阵运算TA=Hfilter，其中：

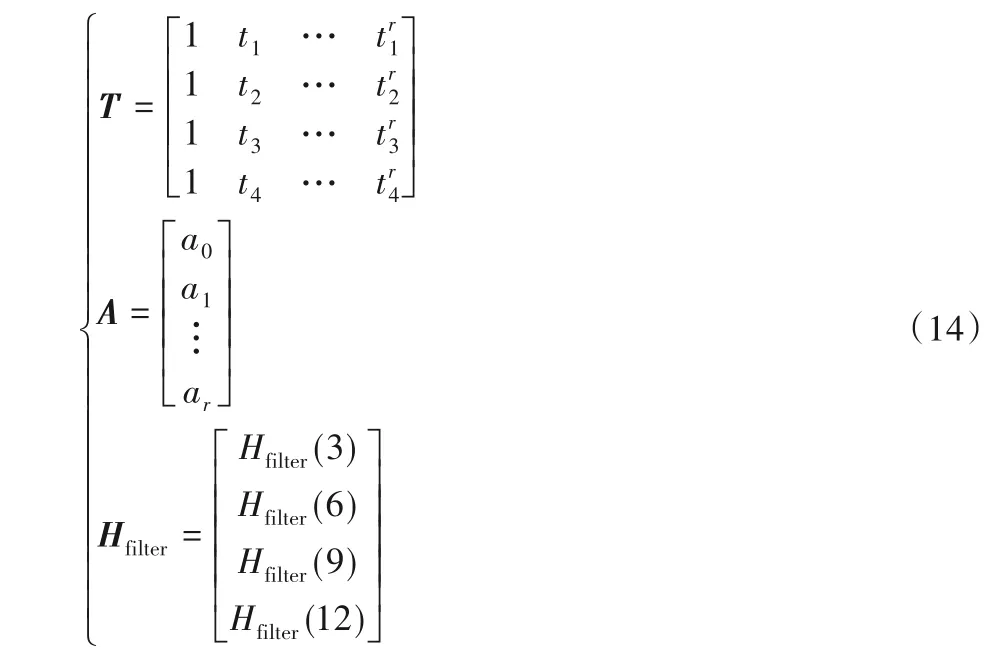
记TT为T的转置矩阵，则有：

记TTT=C，对式（15）两端同乘C-1，得：

由此计算得到系数矩阵A。

在确定多项式最高阶数R的情况下，通过式（12）可以计算得到多项式系数。为了更好地拟合信道变化，在接收端先估计出多普勒频移大小［16］，再根据信道多普勒频移大小来自适应调整多项式拟合的最高阶数R，由于在一个子帧中仅包含4 个块状导频符号，也即一个子载波上仅有4 个不同符号CFR 参考点，因此，多项式的最高阶数不超过3 阶。根据仿真实验最终设置其分段对应关系为：

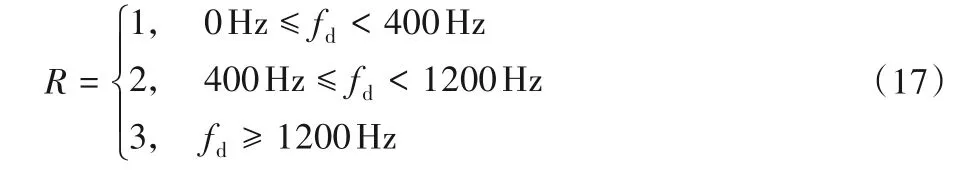
在计算得到拟合多项式后可以通过拟合多项式（11）获取数据符号处的CFR，这样就完成了一个子帧中所有传输符号的CFR估计。

本文方法的信道估计处理流程如下所示。

方法1 基于滑窗滤波和多项式拟合的时变信道估计方法。

输入 频域接收符号向量Y，导频符号矩阵SZC，信噪比SNR，最大多普勒频移fd。矩阵。

输出 滑动窗口长度Lw，多项式阶次R，信道频域响应

步骤1 利用频域接收符号向量Y和导频符号矩阵SZC通过LS方法计算导频符号处的信道频域响应矩阵HLS。

步骤2 采用滑动窗口平滑的思想对HLS进行去噪处理，处理方式如式（9）所示。

步骤3 基于滑动窗口平滑后的信道频域响应矩阵Hfilter，联合理想的信道频域响应矩阵Hperfect计算NMSE，确定各SNR分段下的滑动窗口长度Lw。

步骤4 滑窗滤波处理确定了导频处CFR，接着对每个子载波进行数据符号处的CFR 跟踪，以Tp个导频数据进行多项式拟合，并以式（12）为目标函数，计算多项式系数。

步骤5 根据步骤4 的多项式拟合函数完成一个子帧T个符号的CFR估计，得到信道频域响应矩阵。

步骤6 基于多项式拟合得到的信道频域响应矩阵，联合Hperfect计算NMSE，结合NMSE确定多项式阶次R和最大多普勒频移fd的最佳映射关系。

3 仿真与结果分析

为验证本文方法的有效性，搭建了无线通信仿真系统，仿真参数如表1 所示。仿真系统按照LTE-V2X 标准构建，无线信道采用的是LTE 标准的扩展车辆信道模型（Extended Vehicular A model，EVA）［17］，并根据该模型设定仿真时延为0 ns、60 ns、190 ns、320 ns、390 ns、710 ns、1 100 ns、1 750 ns、2 540ns，相对功率为0dB、-1.5dB、-1.4 dB、-3.6 dB、-0.6 dB、-9.1 dB、-7.0 dB、-12.0 dB、-16.9 dB，根据载波频率和相对终端移动速度设置信道最大多普勒频移fd为1 640 Hz。通过该仿真系统，对比了LS 方法结合线性插值，LMMSE 方法结合线性插值以及本文方法的NMSE和系统BER性能。

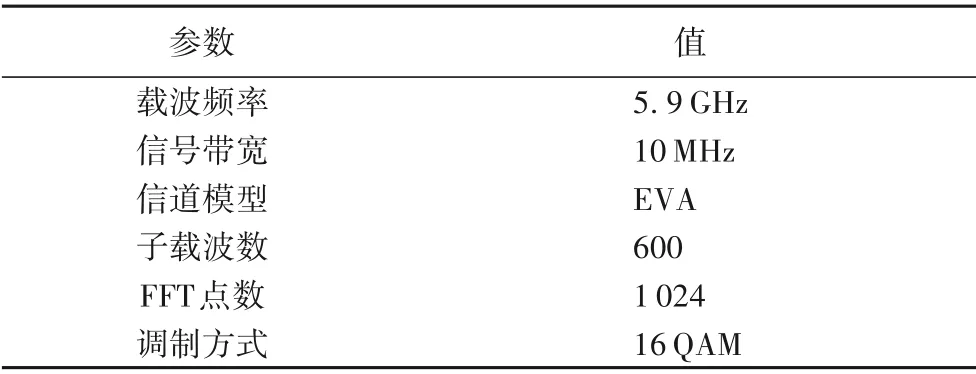
表1 系统参数Tab.1 System parameter

图3 展示了多项式拟合方法在不同最高阶数R条件下，信道估计的NMSE性能随最大多普勒频移大小的变化情况，这是基于SNR=20 dB 的仿真结果。可以看出，在最大多普勒频移较小时，一阶多项式拟合可以取得最低的NMSE结果；在最大多普勒频移在400 Hz～1 200 Hz 时，二阶多项式拟合效果最好；而当最大多普勒频移大于1 200 Hz 时，三阶多项式拟合的性能最优。当终端相对移动速度较小时，信道的时变非常缓慢，甚至是时不变的，因此，采用一阶信道拟合能有最好的拟合效果；而终端移动速度较大时，信道时变剧烈，此时需要用更高阶的拟合多项式才能更有效地跟踪信道的时变特性。

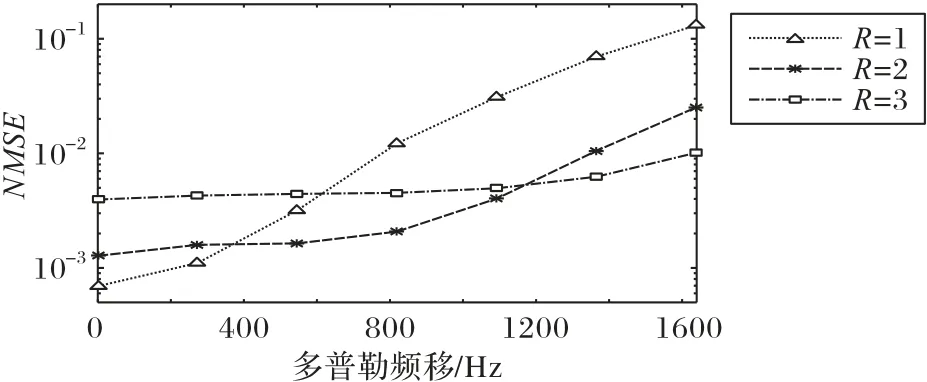
图3 本文方法R=1，2，3时在不同多普勒频移下的NMSE性能Fig.3 NMSE performance of proposed method when R=1，2，3 under different Doppler frequency shifts

图4 是在fd=270 Hz 和fd=1 640 Hz 信道场景下，不同信道估计方法的NMSE性能随SNR变化情况。在终端相对移动速度为50 km/h 时，对应最大多普勒频移，LMMSE 方法联合线性插值的效果最佳，本文方法在LS联合线性插值方法上有一定的性能提升，在不同SNR下，本文方法对比LS 方法都有10 dB的SNR增益。当终端相对移动速度达到300 km/h 时，对应最大多普勒频移fd=1 640 Hz，在低SNR下，仍然是LMMSE 方法的性能最佳，但是随着导频处估计精度的提升，数据处多项式拟合方法的增益逐渐体现，在高信噪比下，本文方法的NMSE性能甚至超过了LMMSE结合线性插值的方法性能。

图4 不同多普勒频移下各信道估计方法的NMSE性能Fig.4 NMSE performance of channel estimation methods under different Doppler frequency shifts

图5 是在fd=270 Hz 和fd=1 640 Hz 条件下，不同信道估计方法的BER性能随SNR变化情况，图5 中理想信道估计是指利用仿真时的理想信道CFR 进行信道均衡后的系统BER结果。在最大多普勒频移较小时，LMMSE 方法和本文方法都非常接近理想信道估计下的BER性能，本文方法对比LS联合线性插值在SNR=20 dB 时有着3 dB 的增益。而在最大多普勒频移较大时，本文方法的性能在高SNR下超过了LMMSE方法联合线性插值的结果。

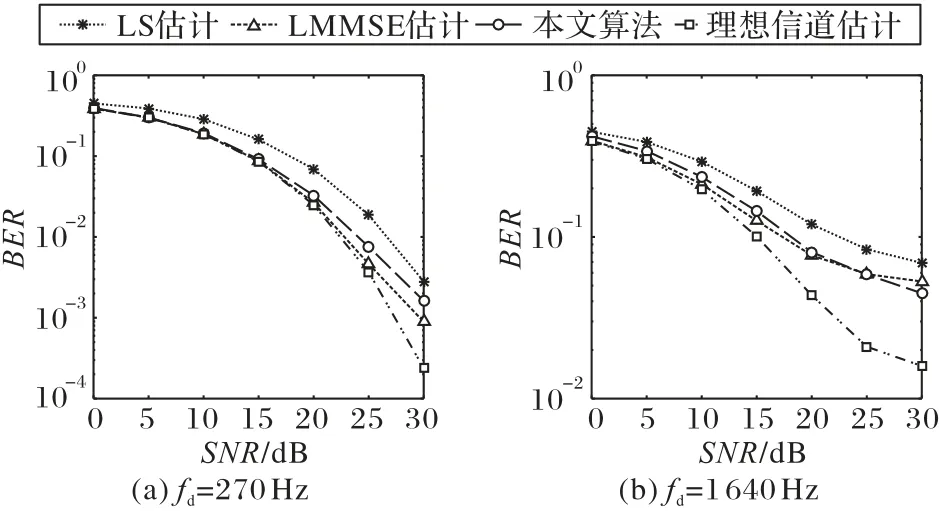
图5 不同多普勒频移下各信道估计方法的BER性能Fig.5 BER performance of channel estimation methods under different Doppler frequency shifts

针对图4～5 可以分析得到，LMMSE 方法在导频位置处是近乎理想的去噪效果，而本文方法在LS方法基础上有一定的去噪效果。对于数据处CFR 的跟踪效果，线性插值在比较小的多普勒频移下还是能有比较好的估计性能，但随着终端相对移动速度增加，信道变化剧烈，线性插值就不能很好地跟踪信道变化，而本文提出的多项式拟合方法能更好地拟合信道时变特性，在数据处的CFR估计是更优于LMMSE方法联合线性插值，因此本文方法在高速移动条件下能表现出更好的信道跟踪效果。

4 结语

为了降低导频符号处噪声对LS方法CFR 估计的影响，并更好地拟合数据符号处V2X 信道时变特性，本文提出了一种基于滑窗滤波和多项式拟合的时变信道估计方法。首先，采用自适应窗口大小的滑动窗口滤波对LS 方法的估计结果进行降噪处理；另外，根据终端移动速度不同设计了自适应阶数的多项式拟合方法完成信道跟踪。仿真表明，本文方法在高速移动环境下的性能表现甚至超过了LMMSE 结合线性插值方法。然而通过BER 曲线可以看出，几种方法对比理想信道估计下的BER 还是有一定的性能差距，设计更优的去噪方法和信道拟合方法是我们下一步的研究目标。