基于级联混沌系统的分数域语音加密算法

徐丽云，闫 涛，钱宇华

（1.山西大学大数据科学与产业研究院，太原 030006；2.山西大学计算机与信息技术学院，太原 030006）

（*通信作者电子邮箱xuliyun@sxu.edu.cn）

0 引言

密码技术作为信息安全领域的研究核心，具有保障数据信息安全的重要作用。语音加密早期主要应用于军事保密领域，保障军事信息的安全传递。信息加密之后，能有效地防止保密信息被人窃取破译，目前信息加密技术在个人应用领域逐步深入。近年来，通信技术飞速发展，其中便捷的语音通信成为人们信息交流的最常用方式之一，这也促使语音通信的安全性逐渐受到个人关注［1］。尽管目前针对语音加密方法已经有诸多研究，但是破解技术也在不断发展，研究更方便快捷且具有更高安全性能的语音加密方法依然是通信安全中的重要内容之一。

混沌系统因其随机性、不可预测性、低计算复杂度，以及对初值和参数极度敏感等良好特性，被广泛应用于通信安全、信息隐蔽等领域中［2-5］。随着对混沌理论的深入研究可知，基于单纯的混沌系统的加密技术在安全性方面表现出一定的局限性，比如易被选择性明文攻击破解等。为了在混沌系统基础上进一步提高加密技术的安全性，研究者们提出了一些改进方法：一方面是对混沌系统进行安全性能的提升，如多个混沌系统叠加使用、利用混沌系统级联方案等。针对级联混沌系统，文献［6-7］对其进行了详细的研究和性能的推导，结果表明级联方案能够提高混沌的Lyapunov 指数，扩大混沌映射及满映射参数范围，具有良好的动力学特性，能够优化系统的安全性能。目前基于级联混沌系统的加密技术已经有研究应用于语音、图像、视频等加密领域，并取得了较好的加密效果［8-10］。另一方面是将混沌系统与其他方法相结合，如对信号进行变换后在变换域进行混沌加密等，从而扩大了密钥空间，提高了安全性能。

针对数字化的语音信号的加密方法主要可分为时域加密、频域加密和时频域组合加密。其中，时域加密方法以置乱和单纯混沌加密为主，密文有时会携带原信号的部分信息，易受选择明文攻击，语音恢复有时不理想、安全性低。频域加密方法通常是对信号进行傅里叶变换，在频域进行置乱加密等，并逐渐发展到在小波变换、余弦变换等变换域实现加密效果［11-13］。变换域加密方法在一定程度上增加了算法的复杂性，在密码分析者不熟悉的变换域进行加密处理能提高保密性能。分数傅里叶变换是经典傅里叶变换的广义形式，在对复杂信号进行处理以及时频分析中能得到更精细的特征［14-15］。近年来，基于分数傅里叶变换的分数域信号处理方法及应用飞速发展，得到广泛关注。已经有许多学者将分数傅里叶变换应用于加密技术，并对分数傅里叶变换在加密中的作用和优势进行了详细的实验与分析［16-20］。然而基于分数傅里叶变换的加密研究主要集中于图像加密和视频加密，在语音通信加密中的研究比较有限。金建国等［20］研究了基于混沌调制分数旋转因子的语音加密方法，但是仅使用了单纯的混沌序列对分数变换阶次进行加密，有一定的安全缺陷，旋转因子易受明文攻击。而针对视频图像的基于级联混沌的分数域加密方法中，需要先进行固定阶次的分数傅里叶变换，分数变换阶次与混沌系统相互独立，并且过程中包括二次加密和解密［9］。以上基于分数傅里叶变换的加密算法中，在进行分数傅里叶变换时利用的是特征分解型离散算法，此算法虽然具有旋转相加性，但计算量较大，在数据量较大情况下，对于实时通信加密有一定的制约作用。

结合级联混沌系统和分数傅里叶变换的优势，本文提出了一种改进的分数域语音加密算法。该算法将级联混沌与分数傅里叶的变换阶次相耦合，即分数变换阶次取决于级联混沌系统，并在分组语音传输过程中呈动态变化，进而增大密钥空间，加强安全性。另外，在对语音信号进行离散分数傅里叶变换时，利用计算量更小的采样型离散算法，为实时通信加密提供更强的安全性和便利性。

1 相关知识

为更清晰地描述本文提出的语音加密算法，本章首先对算法中所使用的级联混沌系统及分数傅里叶变换的离散算法进行详细介绍。

1.1 级联混沌系统

离散混沌系统算法简单，具有运算速度快、序列码率高的优点，但是其Lyapunov 指数小、密钥空间较小，使得其安全性极大降低。级联混沌系统能够提高系统的初值敏感性，成倍提高Lyapunov 指数，并且能够扩大混沌映射及满映射参数范围，因而能够很大程度改善系统的随机性或安全性［6-7］。用Hm(x)表示由m个Logistics 混沌模型组成的级联系统函数，则其可以表示为：

其中：xi+1=fj(μj，xi)=μjxi(1-xi)，j=1，2，…，m，表示第j级子系统函数，在之后描述中用xi(j)表示第j级子系统的第i个输入。从函数表达可以看出，级联混沌中第j级子系统的第i个输出是第j+1 级子系统的第i个输入，并且最后一个子系统即第m级子系统的第i个输出是第1 级子系统的第i+1 个输入，从而达到循环驱动的效果。级联混沌模型的图形表达如图1所示。

1.2 分数傅里叶变换的离散算法

分数傅里叶变换的离散算法主要有三种类型：采样型、线性加权型和特征分解型［14］。线性加权型离散算法因其不能逼近连续分数傅里叶变换，因此使用率不高。特征分解型离散算法满足旋转相加性且表达式简单，并且在已有的语音信号加密相关算法中被采用；然而与其他类型的离散算法相比，其计算复杂度相对较高，为O(N2)。在采样型算法中以Pei 等［15］提出的采样型算法使用最普遍，虽然其不满足旋转相加性，但是具有正交性和可逆性，并且通过一定转换能够从一个分数域得到另一个分数域的结果，具有O(NlogN)的计算复杂度，与快速傅里叶变换具有相同的计算复杂度。与特征分解型离散算法相比，计算速度更快，这对于实时通信来说更具有便利性，因此，本文在语音信号加密中使用采样型离散算法对信号进行分数傅里叶变换处理，以减少算法的计算量。

分数傅里叶变换的采样型离散算法的正变换和逆变换表达式如下：

其中：α表示分数变换阶次；Δt和Δu分别为时域和分数域的采样间隔；n=-N，-N+1，…，N为时域采样点数；m=-M，-M+1，…，M为分数域采样点数。

2 级联混沌系统的语音加密

根据第1 章描述的级联混沌系统和分数傅里叶变换，设计基于级联混沌系统的分数域语音加密算法，信号加密和解密模块总体模型如图2所示。

图2 语音信号加密/解密模块Fig.2 Audio signal encryption/decryption module

系统中，将输入的语音信号首先进行模数转换，得到数字语音信号y。语音信号y通过加密系统，同时完成基于级联混沌系统驱动的分数傅里叶变换及加密处理，得到密文C。将密文通过信道传输到接收端，利用级联混沌对密文进行分数傅里叶逆变换及解密操作，得到解密后的语音信号y′。通过数模转换系统，可得到模拟的语音信号，再由播放器进行输出。

具体加密算法步骤如下：

步骤1 对数字语音信号采用分组加密的思想，每组语音信号包含N个数据，原则上N为级联混沌系统个数m的整数倍，即为整数。

步骤2 设置m个级联混沌系统的初值参数，级联混沌系统的驱动量由初始混沌系统x1(0)=f0(μ0，x0)=μ0x0(1-x0)获取，即给定参数x0、μ0及μ（jj=1，2，…，m）。

步骤3 初始混沌系统迭代N1次得到(0)，达到充分混沌状态。令α1=(0)⋅π作为分数傅里叶变换的变换阶次，利用式（2）对第一组语音信号y=y(1)，y(2)，…，y(N)获取α1阶次的分数域序列，即分数域谱数据序列。

步骤4 由xN1(0)驱动级联混沌系统，循环迭代级联系统次，利用得到的混沌伪随机序列对语音信号分数域谱进行异或操作加密，获取第1组语音信号对应的密文序列如下：

其中：密文序列表示为C1=C1(1)，C1(2)，…，C1(j)，…，C1(N)；f l=f1(μ1，xl(1))，f2(μ2，xl(2))，…，fm(μm，xl(m)) 表 示第l次循环的级联混沌系统，l=0 表示由初始值驱动的级联系统；⊕表示逐位异或运算。

步骤5 第一组语音数据加密完成后，利用最后一个子系统输出的混沌数xN/m(m)作为新的初始值驱动下一组语音数据的级联加密序列，此时分数域语音序列的分数变换阶次变更为α2=xN/m(m)⋅π，并根据后续循环迭代得到的混沌序列获取下一组语音密文。

步骤6 重复步骤5，获得后续所有分组语音信号的加密密文，直到语音信号加密传输结束。

上述对基于级联混沌系统的分数域语音信号加密算法进行了详细的描述，具体的加密过程如图3 所示。接收端在获取密文以及混沌系统的参数即密钥之后，可对密文序列进行解密恢复原语音信号。解密过程即为加密过程的逆过程，可实现密文传输过程中分组语音数据的实时解密。

图3 基于级联混沌系统的分数域语音信号加密过程Fig.3 Encryption process of fractional domain radio signal based on cascaded chaotic system

3 加密算法数值实验效果

为验证本文设计的语音加密算法的有效性，本章选取一段语音信号进行加解密的数值实验。实验通过Matlab软件实现，信号的加解密效果除了主观评价之外，利用均方误差和平均失真程度两个指标进行客观分析。

3.1 语音信号加解密效果实现

为更方便清晰地展示加密算法的加解密效果，实验中截取语音信号的6 675个采样点数据作为明文数据，并将数据分成3 组进行级联混沌加解密。图4 为语音信号明文波形。初始混沌系统的初值参数设为x0=0.1，μ0=3.95。设置级联混沌系统包含5 个子系统，其混沌参数分别为μ1=3.81，μ2=3.90，μ3=4.00，μ4=3.70，μ5=3.93。

图4 原始语音信号波形Fig.4 Original audio signal waveform

在初始混沌系统达到充分混沌状态后，得到第一组语音数据的分数变换阶次，利用采样型离散分数傅里叶变换获取语音信号的分数域谱数据。驱动级联混沌系统，获取的混沌序列对分数域语音信号加密，得到第一组语音密文。继续迭代级联混沌，获取后续两组数据的变换阶次及其密文。图5为语音信号加密前的分数域谱，图6 为加密后的分数域谱，图7 为加密后的时域语音信号。对比图5 和图6 可看出，加密后的分数域谱具有相对均匀分布的特点，不再具有原语音信号分数域谱特征。相应地，对比图7 和图4 可以看出，加密后的时域语音信号波形与原信号波形也具有较大差距，加密信号所残留的原信号信息很少，因此能达到较好的保密效果。

图5 语音信号的分数域谱Fig.5 Fractional domain spectrum of audio signal

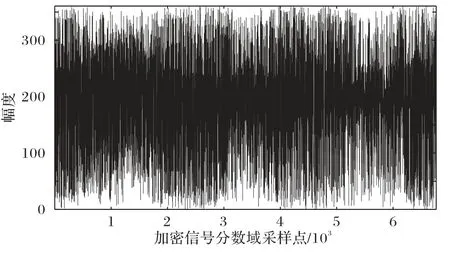
图6 加密后的分数域谱Fig.6 Encrypted fractional domain spectrum

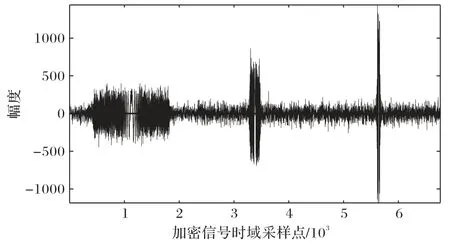
图7 加密后的语音信号波形Fig.7 Encrypted audio signal waveform

加密过程结束之后，加密后的语音信号分数域谱作为密文传输，在接收端对密文进行解码处理。当密钥正确时，可得到正确的解密后的分数域谱及对应的语音信号，如图8和图9所示。当密钥具有一定误差时，解密出的语音信号如图10 所示。将图10与原信号波形图4相对比，从直观上来看，当密钥不正确时，解密语音信号波形变化较大，已经严重失真。

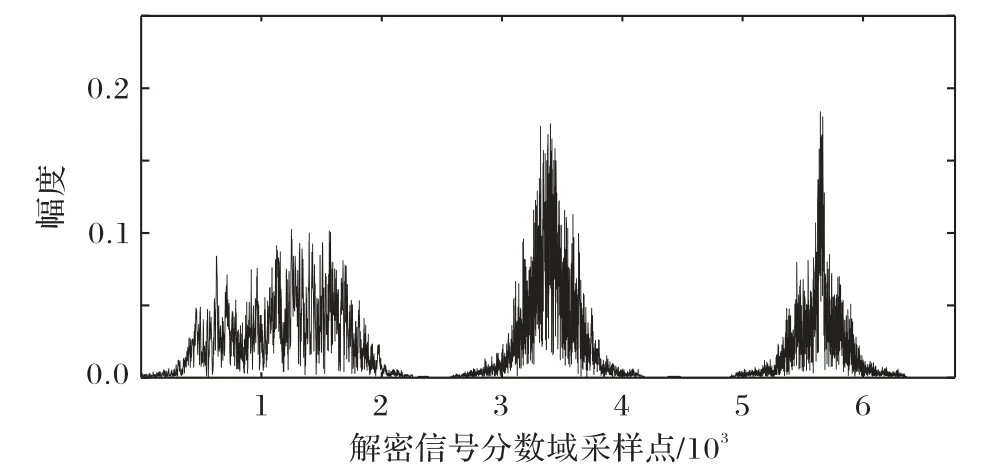
图8 解密后的分数域谱Fig.8 Decrypted fractional domain spectrum

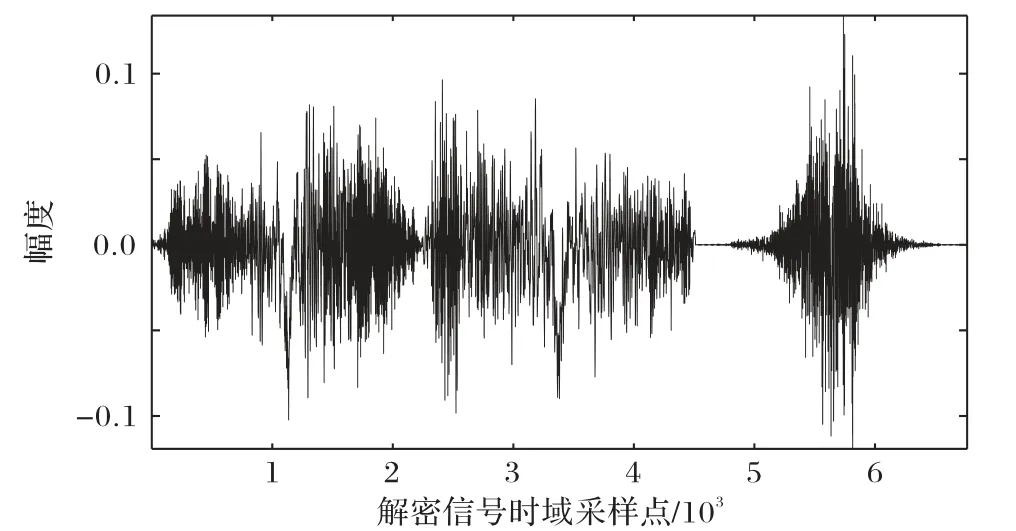
图10 错误解密后的语音信号波形Fig.10 Incorrectly decrypted audio signal waveform

3.2 解密信号均方误差和平均失真效果分析

加密算法的加解密效果除了直观上的评价之外，可以通过客观数据进一步衡量表达。这里采用信号的均方误差（Mean Square Error，MSE）和平均失真（Normal Average Distortion Metric，NADM）两个指标来客观评价加解密效果，均方误差和平均失真的计算式如下：

其中：y'(n)和y(n)分别表示解密的语音信号和原始语音信号的幅度；N表示信号长度即总的采样点数。

为更清晰客观地表达对比效果，除了计算和对比上述实验中图9～10 正确解密和错误解密的均方误差和平均失真之外，又增加了三段不同语音数据进行实验对比，计算结果如表1所示。

表1 正确解密和错误解密信号的均方误差和平均失真对比Tab.1 Comparison of MSE and NADM between correctly and incorrectly decrypted signals

从表1 可以看出，正确解密后信号的均方误差与错误解密时的均方误差结果至少相差两个数量级。从平均失真程度来看，错误解密信号的失真程度相较正确解密来讲，也相差一个数量级。两个客观指标数据的对比表明，错误解密时获取的信号失真程度较大，不能得到原信号的有用信息，因此所设计的加密算法具有较好的安全性。

4 算法性能分析

算法的性能分析主要包括对算法的加密密钥敏感度分析、统计分析、密钥空间分析和复杂性分析。在密钥空间分析和算法复杂性分析中，将本文算法与文献［10，20］中的加密算法进行了对比分析。多角度的性能分析结果表明，本文所设计的加密算法对密钥具有极高的敏感度，能够扩大密钥空间，有效抵御统计性攻击，节省了加密开销，提高了加密系统安全性。

4.1 算法敏感度分析

4.1.1 混沌系统密钥敏感度分析

级联混沌系统的参数作为加密密钥，对系统的安全性起着至关重要的作用。对初始混沌系统的初值和参数及级联系统中各子系统的参数分别进行波动变化，其中一个参数波动，其余参数保持不变，对算法的解密效果进行分析。其中，参数的波动变化为Δμ=10-（nn=8，9，…，17），计算对应解密信号的均方误差，变化曲线如图11 所示（因各个参数波动变化具有相似的结论和效果图，这里不再重复给出）。可以看出，当n<16，即混沌参数波动大小Δμ>10-16时，解密语音信号具有较大的均方误差，信号出现失真效果，加密方法对混沌系统参数具有极大的敏感性。对于包含多个参数的级联混沌系统而言，任何一个参数的波动都会引起解密误差，因此整个级联系统对算法是具有极大敏感度的，这也突出了级联混沌系统的一个优点。

图11 混沌参数波动数量级与均方误差关系Fig.11 Relationship between order of magnitude of chaos parameter fluctuation and MSE

另一方面，级联混沌系统包含多个混沌参数，当获取系统的所有参数以后，如果级联系统的级联次序不正确，也无法对加密信号进行正确解密。将第3 章实验中级联系统的后两个参数进行顺序调换，仅对第一组信号进行实验对比，得到的解密信号与原信号的对比结果如图12 所示，解密后的信号与原信号相比完全失真。可见级联系统参数次序对解密效果有严重影响，即使获取了级联混沌系统的所有参数，在次序不正确的情况下也无法进行正确解密。因此级联混沌系统的存在，进一步提高了密文的破解难度，同时也提高了安全性能。

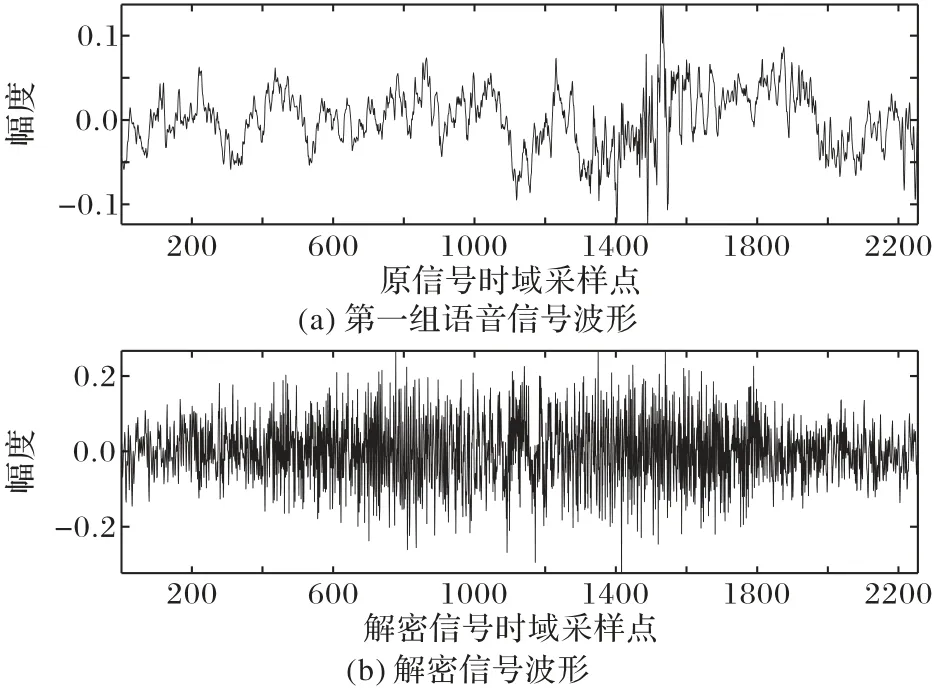
图12 参数次序错误时解密语音信号与原信号波形对比Fig.12 Waveform comparison of decrypted audio signal and original signal when order of parameters is incorrect

4.1.2 分数变换阶次敏感度分析

在加密算法中，语音信号分数傅里叶变换的变换阶次依赖于混沌系统，并随着数据增大不断变化。为测试分数阶次的敏感度，仅对第一组语音信号的加解密进行分析。分数阶次的偏差范围在[-0.01，0.01]，分数阶次每改变0.001，对解密信号的均方误差记录一次，由此得到分数阶次偏差与均方误差的关系图，如图13 所示。由图13 可以看出，随着分数阶次偏差的增大，解密信号与原信号的均方误差迅速增大，解密语音信号失真程度增大，加密算法对分数变换阶次具有极大的敏感度。

图13 分数阶次偏差与均方误差关系Fig.13 Relationship between deviation of fractional order and MSE

4.1.3 分组数据采样点数敏感度分析

在加密算法设计中，分数变换阶次不仅与级联混沌系统相关，也与每组语音数据的采样点数相关，由此实现语音传输过程中各组数据的变换阶次不同，使其呈现动态变化趋势。即使窃密者截获密文数据，并且在已知级联混沌系统参数的情况下，如果每组语音数据的采样点数未知，最多可以解密第一组语音数据。而后续语音数据的分数阶次密钥将产生偏差，并且呈现连锁反应，每组语音信号都会出现解码失真现象并且向后传递，误差不断扩散。图14 显示，在第一组语音信号仅仅减少1 个采样点的情况下，引起后续密文分数阶次的偏差，从而造成后续解密语音信号解码错误。从图14 与图4的对比波形可以看出，仅有开始部分语音信号解密正确，后续语音波形变化较大，均方误差达到RMSE=1.40 × 10-3，解密信号已经严重失真。

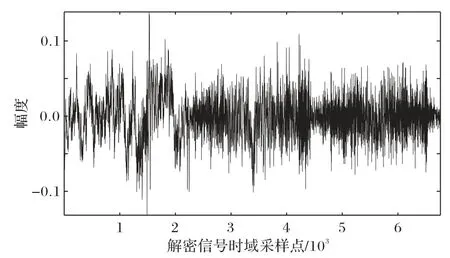
图14 分组数据采样点个数变化时的解密信号波形Fig.14 Decrypted signal waveform when grouped data sampling point number changes

4.2 统计分析

4.2.1 直方图对比分析

将原语音信号及加密后的信号对应的时域波形图4 和图7，分数域谱图5和图6进行直方图显示，结果如图15～16所示。通过对比加密前后幅值的直方图可以看出，加密前信号时域波形的幅值集中分布在区间（-0.2，0.2），而加密后的信号时域幅值范围显著增大，集中分布在区间（-1 000，1 000），加密前后波形幅值分布具有显著差异。

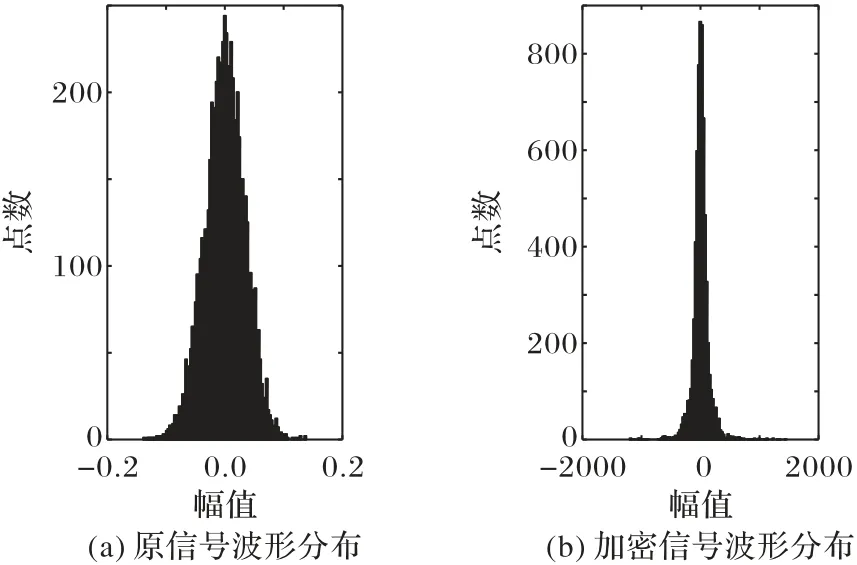
图15 原信号和加密信号波形直方图对比Fig.15 Comparison of waveform histogram between original signal and encrypted signal

加密算法中，实际执行加密操作是在分数傅里叶变换域中。对加密前后信号的分数域谱直方图进行对比，如图16 所示，加密前的分数域谱集中分布于区间（-0.2，0.2），而加密后的分数域谱范围显著增大，并在区间范围内呈现均匀分布特点，能掩盖有效频谱信息，增强信息安全性。

图16 原信号和加密信号的分数域谱直方图对比Fig.16 Comparison of fractional domain spectrum histogram between original signal and encrypted signal

通过直方图的对比可知，语音信号在加密前后时域波形及分数域谱都具有显著差异，加密后的直方图分布特征表明加密算法能有效地抵御统计攻击，具有较好的安全性。

4.2.2 相关性分析

语音信号在相邻的幅值之间通常具有一定的相关性，加密的目的之一就是减少相关性，打乱有用信息，提高安全性。相关系数可用来衡量幅值之间的相关性，对语音信号加密前后的相邻幅值之间的相关系数进行如下计算：

其中：xi和yi表示第i对相邻幅值，和分别为二者的均值；N表示信号长度即采样点数。对4 组不同语音信号计算加密前后的相关系数，结果如表2 所示，可以看出加密前相关系数接近于1，信号幅度具有高度相关性，加密后的相关系数接近于0，几乎不相关，信号在时域达到了充分混乱的效果。图17 为加密前后相邻信号波形的相关性图，其中横坐标表示信号第n点的幅值，纵坐标表示其相邻点第n+1 点的幅值，n=1，2，…，N。可以看出，加密前信号具有线性相关性，而加密后的这种相关性不再显著。

图17 原信号和加密信号波形的相关性对比Fig.17 Correlation comparison between waveforms of original signal and encrypted signal

用上述方法继续分析语音信号分数域谱在加密前后的相关性，相关系数计算结果如表2所示，相关性图对比如图18所示，横纵坐标分别对应相邻点的分数域谱。信号的分数域谱相较于时域信号幅度而言，不再具有强相关性，具有比较集中分布的特点，而加密后的分数域谱相关性呈现出更为显著的均匀随机分布状态。

表2 加密前后相邻幅值相关系数对比Tab.2 Correlation coefficient comparison of adjacent amplitude before and after encryption

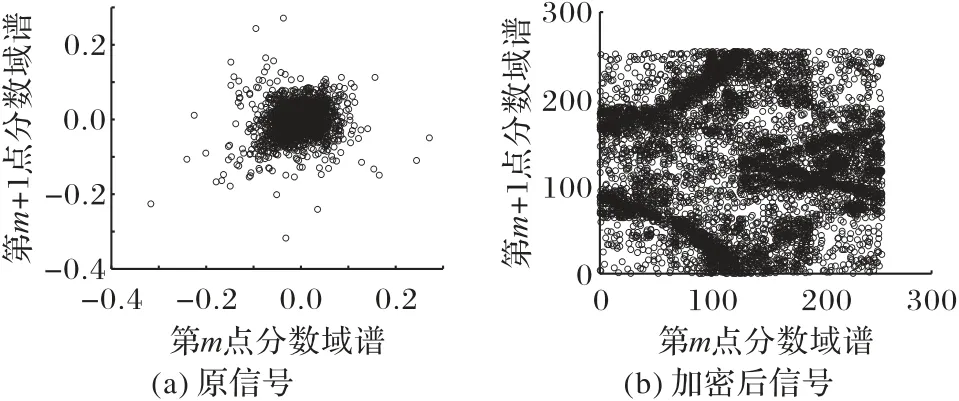
图18 原信号和加密信号分数域谱的相关性对比Fig.18 Correlation comparison between fractional domain spectrums of original signal and encrypted signal

通过相关性的分析和比较可知，无论是时域语音信号还是信号的分数域谱，在加密前后的相关性都具有显著的变化，这使得语音的统计信息在加密后能得到充分隐藏，从而可以更有效地抵御统计攻击。

4.3 密钥空间分析

本文算法的密钥包括级联混沌系统的初始系统的初值x0、参数μ0和所有子系统的参数μ，以及分组数据采样点数N。混沌系统状态值x0的取值范围一般为（-1，1），采用精确到小数点后15 位的双精度浮点型数据时，密钥空间可达到2 ×1015。根据对级联混沌系统参数的敏感度分析可知，当对其中一个参数值变化超过10-16时，或级联系统的次序不正确时，加密信号都不能正确解密，因此整个级联混沌系统使得算法的空间大小达到2 × 1015× 1016×6× 6！=2 × 6！× 10111（以本文实验包含1个初始系统和5个子系统为例）。再加上算法对分数变换阶次的敏感度在10-3以上，以及对分组采样点数的敏感度，将进一步增大算法的密钥空间大小，从而可以有效抵御穷举攻击，增大算法的破译难度，提高算法的安全性能。

可以看出，级联混沌系统的子系统个数越多，密钥空间越大，安全性越好。文献［20］算法中用单个混沌系统对分数变换阶次调制，其密钥空间仅包含一个混沌系统参数。文献［10］算法虽然使用了级联混沌系统，但是在傅里叶变换域也就是频域加密。本文算法在级联混沌系统调制下，在动态变化的分数域进行加密，由于分数阶次的存在及其敏感度的影响（已在4.1.2 节进行分析），将进一步增大密钥空间，因此与上述两种已有算法相比，基于级联混沌系统的分数域加密算法具有更好的安全性。

4.4 算法计算复杂度分析

分数域加密算法与时域加密相比，在算法实现上需要进行变换操作，虽然有变换操作的增加，但敏感度和密钥空间分析也表明安全性有一定提高。另外，本文使用的分数域加密算法是基于分数傅里叶变换的采样型离散算法，具有与快速傅里叶变换相同的计算复杂度即O(NlogN)，而文献［20］中基于分数傅里叶变换的加密算法通常选用特征分解型算法，其复杂度为O(N2)。为更直观体现本文算法的计算优势，对文献［10］算法、文献［20］算法、本文算法（使用采样型离散算法）以及用特征分解型离散变换实现本文算法（记为特征分解型算法）进行算法加解密耗时分析对比。实验中选择对两段采样数分别为3 600 和6 000 的语音信号进行加解密，通过10 次实验计算平均时间，实验对比结果如表3所示。

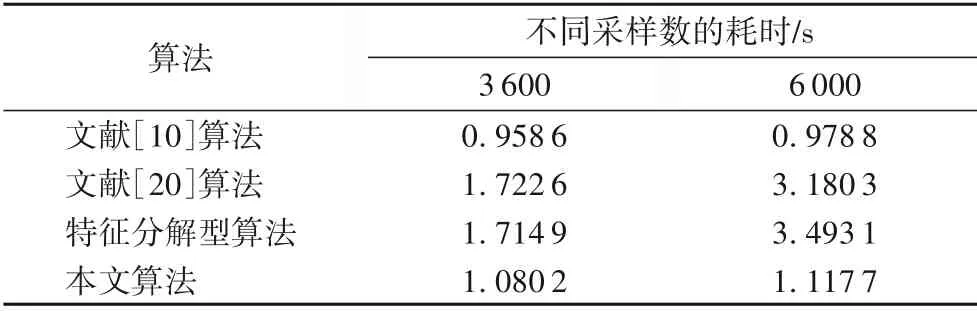
表3 不同算法加解密耗时对比Tab.3 Encryption/decryption time comparison of different algorithms

从耗时对比可以看出，使用采样型离散变换的本文算法在计算量上相较特征分解型具有一定的计算优势，能够节省加密开销，并且这种优势会随着采样点数也就是数据量的增大表现更为明显。尽管采样型离散变换复杂度与快速傅里叶变换相同，但是与文献［10］中单纯的在傅里叶变换域加密算法相比，分数域加密算法因为分数阶次的存在，其较强的敏感度使得密钥空间进一步增大，提高了算法的安全性，相较在频域加密更有优势。

5 结语

为使语音信息可以在信道中安全传输，本文提出了一种新的基于级联混沌系统的分数域语音加密算法。该算法设计中将分数傅里叶变换阶次与混沌系统相耦合，并采用采样型离散算法，数值实验结果验证了所提加密算法的有效性，算法性能分析也从多角度表明了该算法具有较好的安全性。该算法在级联混沌系统和分数傅里叶变换的共同作用下，对密钥具有极高的敏感度，在扩大密钥空间的同时能抵御统计攻击并降低算法复杂度，且在保证系统安全性的同时能更好地匹配实时通信需求，具有较好的应用前景。此外，算法性能分析结果也表明分组加密的采样点数对算法具有较强敏感度，在本文给出的加密算法中对于每组语音信号采用了相同的采样点数，在接下来的应用中如果分组语音信号的采样点数动态变化，将会进一步增大密钥空间并提高算法的安全性能。