相似性特征对链路预测的影响与增强

蔡 彪，李蕊岑，吴媛媛

（成都理工大学计算机与网络安全学院，成都 610059）

（*通信作者电子邮箱caibiao@cdut.edu.cn）

0 引言

复杂网络是研究真实世界中各种复杂系统的结构和演化规律的常用工具。许多社会、生物和信息系统都可以被抽象成一个个的网络来对它们加以描述，一个典型的网络是由许多节点和连接两个节点之间的一些边组成，其中节点用来代表真实系统中不同的个体或组织，而边则用来表示它们之间的相互作用。与复杂网络有关的研究越来越受到人们的关注，链路预测是复杂网络的一个重要分支，它的任务是基于已知网络结构［1-3］，挖掘出给定网络中节点之间缺失的链接。对于某些网络，特别是生物网络，如蛋白质-蛋白质相互作用网络［4-6］、代谢网络和食物网，节点之间是否存在连接需要通过大量实验结果来进行推断。已知的实验结果仅仅揭示了巨大网络的冰山一角，但揭示这类网络中隐而未现的链接需要耗费高额的实验成本，如果预测能足够准确，事先在已知网络结构的基础上设计出精确的链路预测算法，则可以大大降低实验成本，而不是逐个地检查所有可能的交互。链路预测因其重大的实际应用价值，成为许多科学分支的共同焦点［7-9］。

传统上，一种有效的链路预测模型是对潜在节点对进行相似性评分，这对节点越相似，它们之间的联系就越紧密，产生链接的可能性也就越大。此类方法可以通过研究网络的结构特征来实现，如三元图［10］、节点聚类［11］、社区结构［12］和环结构［13］等。此外，基于结构层次上节点之间的相似性，也有一系列经典的预测算法，如共同邻居（Common Neighbor，CN）［14］、AA（Adar-Adamic）［15］和资源分配（Resource Allocation，RA）［16］等，它们启发了其他方法［17］。这些主要是通过它们的共同邻居［14-16］、路径［18］以及路径的权重［19］来度量两节点之间的相似性。然而大多数关于相似性的研究只考虑了结构特征，忽视了在创建新的链接时，标签通常也扮演着重要的角色。

标签能够对个人兴趣进行描述，在推荐系统［20-22］中也得到了广泛应用。卜心怡等［23］用微博的粉丝数量、微博数量、关注人数、转发微博数量等作为节点标签进行预测。Schifanella等［24］和Aiello 等［25］直接从社交平台收集节点标签来计算节点标签的余弦相似性［26］。相应的也有通过研究标签来度量节点相似性的方法，如相同标签（Common Tags，CT）［25］和用户标签间的Jaccard 指标（Jaccard index between users’Tags，JT）［27］。这些研究都基于同质性的假设，即具有相似标签的节点倾向于彼此连接。Wang 等［28］提出一个节点的标签不足以描述这个节点，这个节点的邻居节点的标签也具有参考价值，因此，使用每个节点自身的标签及其邻居节点的标签来构造一个标签系统，在标签的基础上增加了结构信息。标签系统间的余弦相似性（Cosine Similarity between Tag Systems，CSTS）算法基于标签系统，通过Cosine 相似性来度量vi和vj两节点标签系统的相似性。CSTS 算法的不足之处在于：在计算标签系统中每类标签的比重时，仅简单计算了这类标签在节点及其邻居节点的节点集合中存在的个数，表示每个节点自身所携带的标签的权值均为1，这意味着每一个节点的标签贡献都是相同的，每个标签都处于同等地位。

共同邻居［14］算法假设两个节点拥有的共同邻居越多，它们越倾向连接，这一方法在很多真实网络中都证明是有效的［29］。基于朴素贝叶斯（Naive Bayes，NB）［30］分类器，在条件独立［31］的假设下，Liu 等［32］设计了局部朴素贝叶斯（Local NB，LNB）模型来研究链路预测问题，并提出了基于局部朴素贝叶斯模型的相似性算法LNBCN（Local Naive Bayes model-CN）。基于以上分析，由于节点自身的重要性的不同，节点所带有的标签的贡献也有所区别，共同邻居节点的标签的贡献应高于其他标签。因此，本文引入了角色函数，在CSTS的基础上，对共同邻居节点的标签进行加权，提出了带权值的标签。本文研究了四个不同领域的真实网络的结构特征，发现在不同的网络中，节点间的标签相似性差异较大。本文从该网络结构特征着手，研究了标签相似性与链路预测间的关系。本文主要工作如下：

1）通过对四个真实网络中标签相似性这一结构特征进行研究发现：在平均Jaccard 相似性较低的网络中，通过使用带权值的标签可以提高节点间标签的相似性，从而提高链路预测的准确率；在平均Jaccard 相似性较高的网络中，在提高相似性的基础上，充分利用结构特征，可以提高链路预测的准确率。

2）本文在标签系统的基础上提出了标签具有角色性，并通过引入角色函数计算标签的权值，提出了加权标签余弦相似性（Cosine Similarity with Weighted tags，CSW）算法用于提高低相似性网络中的链路预测准确性。

3）在高Jaccard相似性网络中，将体现网络结构信息的偏好链接机制引入到节点的相似性计算中，提出了基于偏好链接机制的加权标签相似性（CSW based on Preferential attachment mechanism，CSWP）算法和基于偏好链接机制的标签系统余弦相似性（Cosine Similarity between Tag Systems based on Preferential attachment mechanism，CSTSP）算法，提升了网络中链路预测的准确性。

在真实网络上实验结果表明，相较于其他链路预测基准算法，CSW 算法、CSWP 算法和CSTSP 算法都取得了更好的预测效果。

1 基于网络相似性结构的链路预测算法

1.1 相似性参数对链路预测的影响

本文在现有算法的基础上研究四个来自不同领域的真实网络的结构特征，特别是基于相似性结构特征的CSTS 算法。四个网络的结构参数如表1 所示，其中：|V|是节点数；|E|是链接数；C是聚类系数［33］；kˉ是网络的平均度；ntag是每个节点拥有的平均标签数；Ntag是每个网络中不同标签的数目；J是测量每个链接中两个节点的标签之间的平均Jaccard 相似性［28］，J=；Ti是节点vi的标签集合。

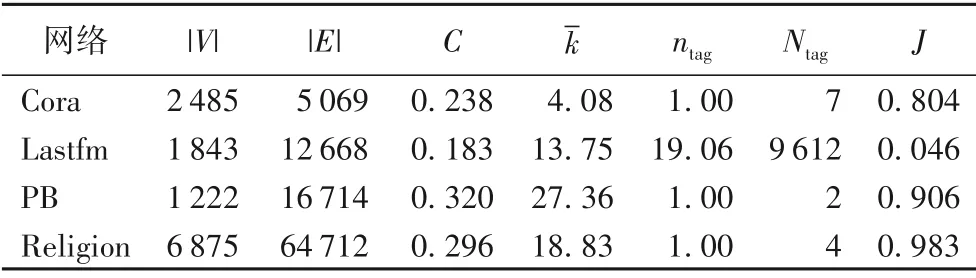
表1 四个真实网络的结构特征Tab.1 Structural features of four real networks

本文主要分析基于相似性的网络结构参数J，如表1 所示，PB（Political Blogs）和Religion 这两个网络上的J值较高，均达到0.9 以上，其次是Cora 网络，相似性达到0.8，Lastfm 网络的相似性最低为0.046。结合相似性参数J和CSTS 算法的研究结果如表2 所示，其中，偏好链接（Preferential Attachment，PA）和RA 为结构性预测算法，CT 和JT 仅基于标签信息，CSTS 在CT 和JT 的基础上，增加了结构信息，提高了节点间的标签相似性。通过分析该结果发现：Jaccard 相似性最大的PB和Religion两个网络采用提高相似性的方法并不能提高预测的准确性，而Cora 和Lastfm 网络通过提高节点之间的标签相似性能够在一定程度提高链路预测的准确性。

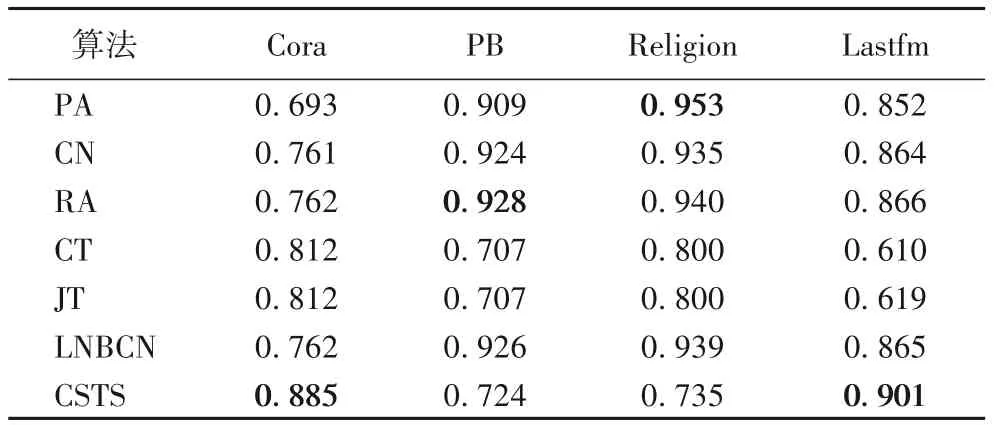
表2 基准链路预测算法与CSTS算法在四个网络上的预测准确性Tab.2 Prediction accuracies of baseline link prediction algorithms and CSTS algorithm on four networks

基于以上分析，本文认为，在网络的链路预测研究中，采用一种算法很难适应不同相似性结构网络中的链路预测，为此提出以下两点假设：

假设1 在平均Jaccard相似性较低（低于0.8）的网络中，使用带权值标签系统可以优化节点间标签的相似性，从而提高链路预测的准确率。

假设2 在平均Jaccard 相似性较高（大于等于0.8）的网络中，在相似性算法的基础上充分利用结构特征可以提高链路预测的准确率。

根据上面提出的两点假设，本文针对不同相似性结构网络设计了相应的算法，以提高链路预测算法的性能。在Jaccard 相似性较低的网络采用加权余弦标签相似性CSW 算法；在Jaccard 相似性较高的网络采用引入偏好链接机制的CSWP 算法和CSTSP 算法，这两种算法在不同的相似性的网络中均能在一定程度上提高链路预测的准确性。

1.2 加权标签相似性CSW算法

为提高较低Jaccard 相似性网络中标签的相似性，本节将通过为标签加权的方式来提高节点间标签系统的相似性。为计算标签的权值，首先计算节点vi的标签系统，方法如下：

其中：Γ(vi)是节点vi的邻居集合。

利用LNB 中角色函数计算每一个共同邻居节点的标签的权值。其定义如式（2）：

1.3 带结构的CSWP算法

本节将研究在平均Jaccard 相似性较高的网络中，将网络结构信息与标签相似性结合形成适合较高相似性网络链路预测方法。为此，在CSW 的基础上，引入偏好链接机制来进行链路预测，增加了网络的结构特征，提出CSWP 相似性算法如下：

其中：ki和kj分别代表节点vi和节点vj的度，在传统研究中通常用于衡量节点的吸引度［34］。CSWP 算法既考虑了结构特征，又结合了节点的标签信息，通过重新定义节点标签系统中标签权重的计算方法，进一步提高了链路预测的准确性，这将有助于理解驱动网络演化的机制。CSWP 算法的实现伪代码如下。

1.4 带权值标签系统实例

为了进一步说明本文的带权值标签系统，下面以一个例子来解释如何构造一个带权值的标签系统。

在图1 中，ta为节点的标签，节点vi及vj的邻居节点标签集为：｛ta，ta，ta，ta，ta，tb，tb，tb，tb，tc，t｝c，则vi的标签系统为：Ai=｛ta，tb，t｝c；节点vi及vj的邻居节点标签集为：｛ta，ta，ta，tb，tc，td，te，tf，tg，th，th｝，则vj的标签系统为：Aj=｛ta，tb，tc，td，te，tf，tg，th｝。其中，vw节点为共同邻居节点，其节点的标签权值为：在基础权值1上加，即5/3，其余节点的标签权值均为1，则vi与vj两节点的标签系统中每一类标签的对应权重分别为：V（it）：｛ta：17/35，tb：12/35，tc：6/35｝，V（jt）：｛ta：11/35，tb：3/35，tc：3/35，td：3/35，te：3/35，tf：3/35，tg：3/35，th：6/35｝。

图1 节点及节点的标签Fig.1 Nodes and node tags

1.5 复杂性分析

2 实验设置

2.1 实验数据

本文的实验数据使用表1 中的四个来自不同领域的真实网络：1）Cora 网络是一个由机器学习相关的论文组成［35-36］的引用网络。每篇论文都被划分到一个特定的类，其中，可能存在的类有：基于案例、遗传算法、神经网络、概率方法、强化学习、规则学习和理论。2）Lastfm 网络是一个从lastfm.com［37］收集的友谊网络，其中每个用户都可以为艺术家分配标签。3）PB 网络是美国政治博客的信息网络［38］，其中每个节点都被标记为“自由”或“保守”。4）宗教网络（Religion）是一个由新浪微博的宗教信徒组成的网络［39］，其中每个用户只有一个信仰，其中可能的信仰包括基督教、佛教、伊斯兰教和道教。其中：Cora、PB 和Religion 网络是定向网络。在实验中，忽略链接的方向，将网络视为无向网络。

2.2 评价标准

任意给定一个无向网络G（V，E），为了测试算法的准确性，本文将已知的链接E随机地分成两部分：训练集ET和测试集EP。训练集被视为已知信息，测试集被用于测试，在计算分数值的时仅使用训练集中的信息，测试集中的任何信息都不允许用于预测。显然，E=ET∪EP，且ET∩EP=∅。在本文的实验中，|ET∶||EP|=9∶1，且保证训练集中不包含孤立节点与图的连通性。本文使用AUC（Area Under Curve）［40］衡量预测算法的准确性。AUC可以理解为在测试集中随机选择链接的分数值比随机选择不存在的链接（即集合UE中的链接，其中U为|V（||V|-1）/2个所有可能链接组成的全集）的分数值更高的概率。在实验的n次独立比较中，如果有n′次测试集中的链接分数值大于不存在的链接分数值，有n″次测试集中的链接分数值与不存在的链接分数值相等，则AUC定义为：

如果所有分数均随机产生，则准确度应该在0.5 左右，因此，AUC高于0.5 的程度表示该算法比随机选择方法准确的程度。每个AUC精度值均为10次独立实验后的平均值。

从泉州志愿服务开展的情况看，大部分志愿活动是由政府部分机构组织的，志愿者也是由政府机关工作人员组成。政府主导和行政推动的方式虽然有利于启动志愿服务活动，但过分依靠行政推动往往会出现“被志愿”或志愿服务形式化或运动化的问题。[7]由于长期的行政化主导，一方面让民众产生误解，以为志愿服务是政府行为；一方面很容易形成运动式，出现形式化的问题；一方面“被志愿”者在心理上对志愿服务活动会产生抵触情绪。

3 实验结果

3.1 带权值标签相似性实验结果

在本文实验中，以J=0.8 为阈值来划分低相似性网络和高相似性网络。由于Lastfm 网络的平均Jaccard 相似性低于0.1，而Cora 的相似性为0.804，均低于PB 和Religion 两个网络的相似性，因此，将本文提出的标签加权CSW 算法与现有的基准算法［41］和未加权的标签算法在Lastfm和Cora网络上进行了实验对比，以此验证假设1 的正确性。每个AUC精度值均为10 次独立实验后的平均值，加粗的值表示在同一个网络中性能最好的算法的平均AUC精度值，相较于其他算法，本文提出的基于加权标签相似的CSW 算法的链路预测准确性最好，对比的实验结果如表3所示。

从表3可以看出，在平均Jaccard相似性较低的网络中，带权值的标签系统通过为标签加权提高了标签系统的相似性，从而提高链路预测的准确性，验证了第2章中提出的第1个假设，在低相似性的网络中，提高相似性可以得到最高的准确性。

表3 CSTS、CSW和基准算法在Lastfm和Cora网络上的AUCTab.3 AUC of CSTS，CSW and baseline algorithms on Lastfm and Cora networks

3.2 引入结构信息实验结果

与Lastfm 网络相比，可以认为Cora、PB 和Religion 这三个网络的平均Jaccard 相似性为高相似性网络结构。本文将CSWP 算法和CSTSP 算法与几个基准算法在这三个网络上进行了实验对比，以此验证假设2的正确性。实验结果如表4所示。在上述多组对比实验中，基于偏好链接机制的CSTSP 和CSWP 的准确性在三个网络中相较于不包含偏好链接机制的CSTS 和CSW 均有较大的提高。在Cora 网络上，CSWP 的预测准确率略高于CSTSP，可以认为预测结果的提高是因为带权值的CSW 算法提升了标签相似性。在Jaccard 相似性大于0.9 的PB 和Religion 网络中，CSTSP 和CSWP 的预测准确性一致。CSW 与CSTS 相比，有较小程度的提升。因此，可以认为在Jaccard 相似性很高的网络中，相似性改变不能明显提高链路预测的准确性，链路预测结果主要由引入的结构信息决定，在提高相似性的基础上引入的结构信息可以得到最高的准确性，验证了第2章中提出第2个假设的正确性。

表4 不同算法在Cora、PB和Religion网络上的AUCTab.4 AUC of different algorithms on Cora，PB and Religion networks

4 实验分析

链路预测算法主要是基于标签信息和结构信息这两个方面设计的，同时，多种有助于链路预测的机制都与标签和结构有关，当网络和算法所遵循的机制一致时，该算法能够提供更加准确的预测。因此，本文将从标签和结构这两个方面对实验结果进行分析。

4.1 带权值标签增强了相似性

4.1.1 带权值标签相似性CSW的分布

根据3.2 节中提出的数据划分方法，将四个真实网络随机划分为训练集ET和测试集EP两部分，训练集被视为已知信息，用来计算测试集中每条测试边关于lg(ki⋅kj)和CSWij的相似性值。Cora、PB 和Religion 三个网络的J值较高，Lastfm 的J值较低，在图2 中Cora、PB、Religion 这三个网络上，CSWij的值大多分布在0.8～1.0，而Lastfm的CSWij的值大多都分布在0.8以下。本文分别计算了四个网络的测试部分的CSWij平均值：在Cora 上为0.882；在Lastfm 上为0.666；在PB 上为0.944；在Religion 上为0.983。同样计算了四个网络的测试部分的Jaccardij平均值：在Cora 上为0.819；在Lastfm 上为0.047；在PB 上 为0.901；在Religion 上 为0.981。CSWij值相较于Jaccardij相似性值均有一定程度的提高，尤其是在Lastfm 中，节点间的标签系统相似性较Jaccardij相似性值改变最明显。

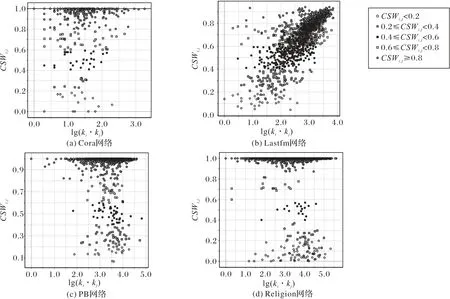
图2 四个真实网络的测试集中组成测试边的节点对间lg(ki ⋅kj)的值与CSWij值的关系Fig.2 Relationship between lg(ki ⋅kj)value and CSWij value of the node pairs that constitute the test edge in the test set of four real networks

4.1.2 标签系统提升了相似性值

接下来分析基于标签相似性的CSTS 和基于带权值标签相似性的CSW 相较于仅基于标签信息的JT 预测算法的相似性。JT算法的预测准确性较低，仅略高于随机预测的准确性。CSTS 和CSW 在CT 和JT 的基础上，将邻居节点的标签也考虑进来。在平均Jaccard 相似性较低的Lastfm 网络中，使用节点邻居的标签信息大幅提高了节点间标签的相似性，如图3（b）所示，与JT 算法相比，CSTS 算法和CSW 算法的相似性有大幅度的提升；在平均Jaccard 相似性较高的网络中，Cora、PB 和Religion 三个网络的J值较高，使用节点邻居的标签信息不同程度地提高了节点间标签的相似性，如图3（a）、（c）和（d）以及表2 与表4 所示，与CT 和JT 相比，CSTS 算法和CSW 算法的准确性相应地也得到了提升；并且，标签相似性越低的网络，通过提高节点间标签的相似性来提升算法的准确性的效果越显著，这一结论在Cora、Lastfm和PB网络上可以得到印证。

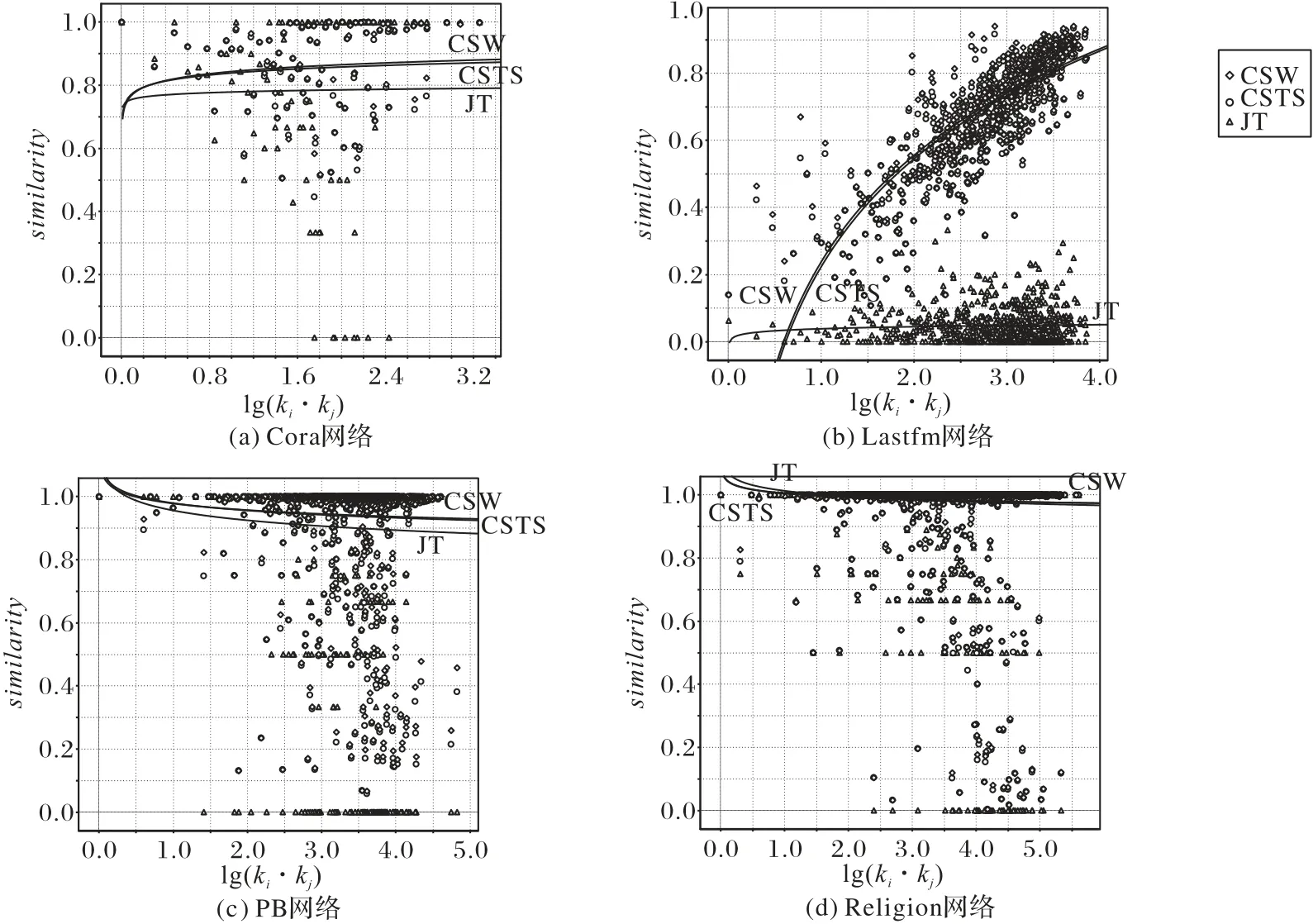
图3 四个真实网络的测试集中组成测试边的节点对间lg(ki ⋅kj)的值与标签相似性平均值的关系Fig.3 Relationship between lg(ki ⋅kj)value and average value of tag similarity of the node pairs that constitute the test edge in the test sets of four real networks

分别用CSW 算法、CSTS 算法和JT 算法计算了四个网络中每条测试边的标签相似性，并对lg(ki⋅kj)值相同的测试边的标签相似性取平均值，用similarity来表示。

4.1.3 带权值标签相似性解决了JT为0的情况

在图3中存在标签相似性为0的情况。因此，本文分别统计了四个真实网络中测试集中的边数（Edges）、测试边CSWij=0 的数量（用CSW（0）表示）、测试边JTij=0 的数量（用JT（0）表示）。实验结果如表5所示。

表5 CSWij与JTij在测试集中值为0的情况Tab.5 Cases where the values of CSWij and JTij are zero in the test sets

分析实验结果发现：在四个真实网络的测试集中，出现大量JTij值为0 的情况，极少甚至没有出现CSWij值为0 的情况。CSW 解决了组成测试边的节点对间因不存在相同标签导致节点的标签相似性为0，进而使产生链接的可能性为0 的情况，算法的准确性也得到了提升。

4.1.4 CSW进一步提升了CSTS相似性值

本文的CSW 相较于CSTS 在一定程度上能够提升预测的准确性。因为CSW 算法在CSTS 算法的基础上引入了带权值的标签，有助于提升存在边的相似性。为了验证该结论，分别用CSW 算法和CSTS 算法计算每条测试边节点对间的标签相似性，对同一条测试边，用CSWij减去CSTSij，得到的差值用D-value进行表示。如图4 所示，D-value的值几乎全部分布于0 刻度线以上，这表明使用带权值的标签加强了潜在节点对间的标签相似性，且Lastfm 的相似性提高更多。基于以上分析，本文验证了假设1 的正确性，在节点间标签相似性较低的网络中，使用带权值的标签，在标签系统的基础上进一步提高节点间标签的相似性从而提高链路预测的准确率。

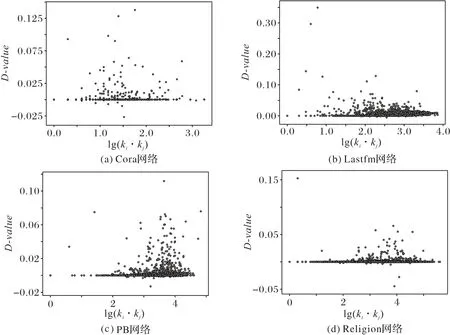
图4 四个真实网络中的测试集中组成测试边的节点对间lg(ki ⋅kj)的值与标签相似性差值的关系Fig.4 Relationship between lg(ki ⋅kj)value and label similarity difference of the node pairs that constitute the test sets of four real networks

计算Lastfm 网络每条链接中两个节点的标签之间的Jaccard 相似性，选取大于等于0.2 的链接组成新的网络Lastfm-2，该网络的平均Jaccard 相似性为0.25。将Lastfm-2网络的链接按训练集和测试集9∶1 的比例划分，训练集被视为已知信息，测试集用来预测，表6 中为CSTS 与CSW 算法在不同网络中的AUC值。

表6 CSTS与CSW算法的AUC比较Tab.6 AUC comparison of CSTS and CSW algorithms

将J为0.046 的Lastfm 网络的平均Jaccard 相似性提高到0.25，在相似性较低的网络中，提高标签的相似性有助于提高链路预测的准确性，同时也表明，CSW 算法在相似性较低的网络中与其他的标签相似性算法相比有更好的表现。

4.2 高相似性网络中结构信息的影响分析

在平均Jaccard相似性较高的Cora、PB和Religion网络中，由于PA、CN、RA 和LNBCN 等算法均是仅基于结构信息的算法，而它们的AUC精度值均高于仅基于标签信息的算法。本文提出的CSWP 在CSW 的基础上引入了偏好链接机制，增加了ki⋅kj，CSWP 中的CSW 包含了同质性机制和聚类机制，既使用了标签信息，又使用了结构信息。

在CSWP 中，当vi和vj两节点间存在共同邻居节点时，本文将共同邻居节点对vi和vj是否产生链接的贡献度量通过其节点所携带标签的权值进行表示；当vi和vj两节点间不存在共同邻居时，CSW 将退化成CSTS，聚类机制将不再发生作用。在计算潜在节点对间形成链接的可能性时，若节点的标签系统间相似性不同，即CSWij值不同，则可以区分多个ki⋅kj值相等的潜在节点对，如图5 所示；当节点对的标签系统间标签种类和对应比重值完全相同时，CSWij值最大为1，两节点吸引力达到最大，为ki⋅kj；相反，若节点对的标签系统间有不同的标签或相同标签对应比重值不同，则这两个节点的吸引力就会降低，将低于ki⋅kj。

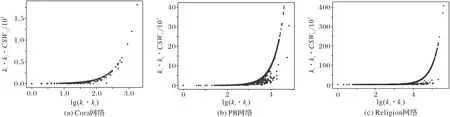
图5 三个真实网络的测试集中组成测试边的节点对间lg(ki ⋅kj)的值与ki ⋅kj ⋅CSWij的关系Fig.5 Relationship between lg(ki ⋅kj)value and ki ⋅kj ⋅CSWij of the node pairs that constitute the test edge in the test sets of three real networks

CSWP 在CSW 的基础上引入了偏好链接机制，CSWP 与基准算法相比较而言，预测准确性最好。同样，本文在CSTS的基础上也引入了偏好链接机制，得到了CSTSP 算法。CSTSP 算法和CSWP 算法在PB 和Religion 网络上的预测准确性相等，在Cora 网络上，CSTSP 的准确性略低于CSWP，该实验结果进一步验证了假设2的正确性。

5 结语

本文主要研究了相似性在复杂网络演化中对链路预测的影响。在标签系统的研究中，忽略了标签的角色性。本文认为，具有不同相似性参数的网络可以采用不同的方法来提高链路预测的准确性，不同节点所携带标签重要性也不同，共同邻居节点的标签的贡献应高于其他标签。本文结合链路预测的多个基准算法以及来自四个不同领域的真实网络的结构特征对标签相似性与链路预测间的关系进行研究，发现网络的标签相似性特征对所采用的链路预测方法有较大的影响，提出了两点假设，并根据这两点假设分别设计了对应的链路预测算法。在四个真实网络上进行的实验结果表明，本文提出的根据不同网络相似性特征采用对应算法进行链路预测均能够得到更准确的预测结果。

由于带权值标签和偏好链接机制均是基于1 阶网络相似性，因此，下一步工作将在本文的基础上研究基于1.5 阶链路预测算法来揭示驱动网络演化的机制；同时，本文中的阈值是根据经验设置的，目前没有合适的实验数据来研究J的不同值对结果的影响，下一步工作还将结合模糊优化理论和合适的网络对其作进一步研究分析。