整合素材 深化模型


【摘要】本文以《相遇问题》的教学设计与评析为例,论述在具体教学中借助多样素材帮助学生理解“相遇问题”,通过问题引入,回顾经验;借助图形,理解模型;多样变式,丰富模型等活动,借助图形操作、直观对比和反思迁移策略,引导学生感悟解决问题中“两积之和”的结构,提升解决问题的能力。
【关键词】《相遇问题》 整合素材 深化模型
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2021)25-0062-04
《相遇问题》是人教版数学四年级上册第四单元《速度时间路程》的课后补充内容。虽然人教版教材中没有相关的教学内容,但五年级上册教材出现了借助《相遇问题》的模型来列方程解决问题的习题。因此,在教学四年级上册教材《速度时间路程》一课之后补充相应的“相遇问题”内容,有利于学生建立相遇问题的模型,深入理解速度、时间、路程之间的关系,为学生后续的学习打下基础。
一、教材分析
针对人教版教材相关习题的分析,笔者认为《相遇问题》的教学可以关注如下四个方面。
(一)关注素材的整合
人教版教材中有大量的好题,虽然这些习题分散在不同单元、不同年级,但它们有着相同的结构,即两积之和的结构。教师在设计教学中需要运用整合教材的方法,把这些习题按照一定的逻辑进行组合,促进学生解决问题能力的提升。而《相遇问题》属于两积之和的模型,教材中有着大量类似的习题,教师通过收集、整合、改编这些素材,有利于加强学生对知识点的理解。
(二)注重图形的表征
浙江省2019年中小学质量监测相关数据显示,四年级学生在利用画图来解决问题的相关能力较为薄弱,即很多学生并不知道如何利用画图表征和分析问题。因此,教师在数学课堂中给予学生更多的借助画图分析和表征问题的机会,会对他们提升问题解决能力有所帮助。
(三)深化模型的理解
四年级学生对“相遇问题”相关知识并不陌生,但他们并不明白为什么可以这样计算、其中有什么联系等。因此,教师要引导学生感悟模型的发生和发展过程,让学生能够把新旧模型、正向逆向模型等进行联系与扩展,从而深入理解《相遇问题》模型问题。
(四)沟通习题的联系
数学知识之间有着千丝万缕的联系,解决数学问题的模型更是如此。如果把相遇问题的模型与生活中其他速度类问题进行巧妙沟通,那么对学生理解该模型、提升解决问题的能力将会有较大的帮助。
二、教学目标
基于以上思考,确定教学目标如下。
1.经历解决具体生活问题的过程,借助实物和图形的直观演示和表征,逐步构建相遇问题的数学模型。
2.经历从问题情境和已有数量关系出发解决新问题的过程,不断深入感悟和丰满模型,有效培养学生利用画图分析解决问题的能力,以及培养学生解决问题的迁移能力。
3.经历不断观察、对比、交流与归纳等学习活动,让学生感受生活问题的数学化,培养学生的数学应用意识和模型思想。
三、教学过程
(一)问题引入,回顾经验
1.口答习题,回顾关系
师:同学们,这里有几个问题,你们能解决吗?(学生逐一回答)
课件出示:
[(1)小明每分钟步行80米,5分钟行多少米?
(2)一辆汽车每小时开40千米,6小时共开多少千米?
(3)火箭速度15千米/时
师:刚才我们解决了这几个问题,那么,解题的过程中你们又是怎么想的呢?
生1:比如第一题,先找到小明每分钟行的路程,再乘时间,就可以算出路程。
生2:就是利用“速度×时间=路程”来解决。
师:是的,我们都是利用了“速度×时間=路程”这个关系来解决问题。
2.沟通数形,回顾线段图
师:我们再来看,第一题可以用这个图来表示吗?
课件变化(隐去第三题的相关信息):
(1)小明每分钟步行80米,5分钟行多少米?
生1:可以的。这里的一小段表示小明每分钟行80米,有这样的5段就是5分钟,可以求出一共行走的路程。
师:很好。那第二题呢,可以吗?
(2)一辆汽车每小时开40千米,6小时共开多少千米?
生2:不行,因为题目中提出开车6小时,而这里只有5段,不能表示。
生3:也可以,只要增加一段就可以了。这一段就表示每小时行40千米,求一共行多少千米?
40千米/时
一共行多少千米?
师:说得很清楚,看来在解决问题时,你们已经学会用线段图来表示题目的意思。
【评析】这三道口答题虽然简单,但能充分调动学生学习的积极性,有效地回顾利用“速度×时间=路程”这个关系来解决问题,以及利用线段图表征问题等经验,为后续的学习打下基础。同时,通过讨论画图为后续的画线段图打下基础。
(二)借助图形,理解模型
1.讨论习题,解读信息
师:刚才我们研究的是一个人、一辆车行驶的问题,现在我们变一下,变成两个人。
课件出示:小明与小红从两家同时出发,相向而行,小明每分钟行80米,小红每分钟行60米,4分钟后相遇,他们两家相距多少米?
师:仔细观察一下,问题中有哪些地方需要注意的?
生1:他们是相向而行。
生2:他们同时出发。
生3:问题是要求两地相距多少米。
……
师:好的。我们一起来看一下动画。(课件播放动画)
2.画线段图,解决问题
师:对这样的问题你能用线段图来表示吗?(生:可以。)请你们先尝试画一画图,然后列式解决问题。(学生操作)
3.数形结合,理解模型
师:老师收集了几种方法,我们一起来看一下。
展示一:
小明:80[×]4=320(米)
小红:60[×]4=240(米)
一共:320+240=560(米)
师:请介绍一下自己的想法。
生1:小明和小红都走了4分钟,所以给两人都画了4段。小明的速度是80米/分,小红的速度是60米/分,所以用80乘4就是小明的路程,60乘4是小红的路程,两个路程相加得出总的路程。
展示二:
(80+60)[×]4=560(米)
生2:我是先求出小明和小红一分钟走的路程,然后用路程去乘他们行走的时间。
师:谁能把他的意思用画图的方式表示出来。
生3:左边一段是小明每分钟行的,右边一段是小红每分钟行的。他们相加就是1分钟共行的路程,一共有这样的四组线段,所以用(80+60)×4=560(米)。
师:是的,这样连一连,可以让我们看得更加清楚。
展示三:
师:为了让大家更容易理解,老师把这样的图“请”到黑板上来。谁愿意再来解释一下这个图是什么意思?
生4:这里的红色一段就是小明的速度,黄色一段是小红的速度,把它们加起来就是一分钟共行的路程。(引导学生移动线段,把图整理如下)
4.对比关系,提炼模型
师:同学们,上面的一组线段是不是更加清楚了?那么这一组线段表示的是什么?
生5:一组线段表示小明和小红每1分钟共行的路程,四组线段表示他们一共行了4分钟。
师:那是不是利用了“速度×时间=路程”这个关系来解决问题?(生:是的。)这里的80+60还叫速度吗?
生1:不是速度了,可以叫速度和。
师:是的。把两个人的速度合在一起就可以叫速度和。它们的关系是怎样的?
生2:速度和×时间=总路程。
师:刚才我们用两种方法都求出了总路程,那么他们之间又有什么不同的地方呢?让我们再来回顾一下。
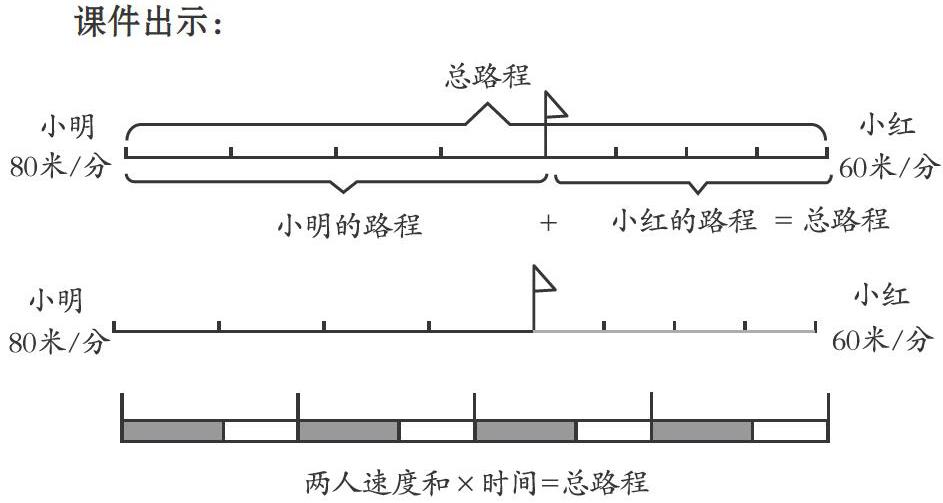
课件出示:
师:是的。第一种方法是用“速度×时间”,算出小明和小红的路程;而第二算法是先求两人的速度和,再用速度和去乘共同行驶的时间,最后算总路程。
【评析】“相遇问题”对学生来说并不陌生,很多学生还会运用“速度和乘时间”求总路程。因此,教师要把教学重点放在理解和沟通“速度和×时间=路程”和原來关系之间的联系和区别。通过引导学生围绕线段说一说、连一连、摆一摆等活动,从多种角度表征和理解速度和,同时开展“速度和×时间=路程”和“速度×时间=路程”的讨论与比较,不断扩展解决问题的结构,使学生深入理解相遇问题模型。
(三)多样变式,丰富模型
1.相反变式,感悟模型
师:接下来,我们继续看大屏幕,题目要变一下。
课件出示:
师:想一想,上面的哪个问题也可以用这个线段图来表示?同桌可以交流一下。
师:现在老师来做个调查,认为第一个可以的请举手,第二个呢?(学生举手)谁愿意来说一说可以怎么表示?
生1:我认为第一个可以,第二个不可以。因为第一个是相向而行,第二个是背向而行。
生2:我觉得第二个也可以,虽然是背向而行,但题目中讲了是从同一个地点出发的。
师:如果背向而行可以表示上面的问题,那么能用“速度和×时间=总路程”来解决吗?
生3:可以的。因为左边这一段就表示80米,右边这一段是60米,把他们相加就是1分钟行的路程,这样一共有5分钟,所以可以用(80+60)×5=700(米)。
课件出示:
师:是的。前面是相向而行(板书),这里是背向面行,虽然行走的方向不同,但他们解决问题的方法却是相同的。
【评析】学习完经典习题之后,笔者设计了一些反向变式,围绕《相背问题》的讨论,让学生再次感受“速度和×时间=路程”的关系,更重要的是让学生感受到:原来这样的相背问题可以运用类似的方法来解决,从而扩充《相遇问题》的内涵。
2.公式变式,全面理解
师:这幅图的意思你们看懂了吗?谁来说说它表示的是什么问题呢?
课件出示:
生1:甲车每小时行60千米,乙车每小时行50千米,两地相距440千米,他们从两地出发几小时后相遇?
师:非常好!我们一起来看课件。
课件出示:
(1)A、B两地相距440千米,甲乙两车同时从两地出发,相向而行。甲车每小时行60千米,乙每小时行50千米。几小时后两车相遇?
(2)小明和小红两家相距360米,他们同时出发,相向而行,小明每分钟走70米,出发3分钟后相遇,小红每分钟走几米?
师:上面两题你们能画出线段图并解决问题吗?(学生独立操作,展示交流。)
师:我们一起来看看这个同学的方法。
展示一:
师:他的方法正确吗?(正确)
展示二:
师:第二题,请大家仔细看一下,问题出在哪里?
生1:150是小红3分钟走的路程,所以150还需要除以3。
生2:这里的150是指上面的一整段,而我们要求的是小红的速度,所以还需要把150平均分成3段。
展示三:
师:再来看看刚才这两种算法,想一想,与我们今天学习的方法一样吗?
生1:第一种方法是求时间,第二种方法是求另一个速度。
生2:第一种用总路程÷速度和=时间,第二种先用总路程÷时间=速度和,再用速度和减去另一个速度。
师:其实你们说得都很有道理。虽然随着条件和问题的變化,我们想到了“总路程÷时间=速度和”和“总路程÷速度和=时间”这两个关系,但它们都是建立在前面关系的基础上进行思考和解决问题。
【评析】上面两道习题是相遇问题公式的变式,通过解决问题,学生可以感悟与提炼不同习题背后的数量关系。同时借助对比与交流,使学生了解到公式之间有着紧密的联系,它们都是由“速度和×时间=路程”演变而来,帮助学生理解不同数量关系之间的联系与区别,促进学生全面深入地理解相遇问题模型。
3.迁移变式,拓展模型
师:同学们,知道今天学习的内容是什么吗?
生1:行程问题。
生2:相遇问题。
师:是的,我们今天学习的就是行程问题中的相遇问题。刚才我们用画图的方法解决了很多行程的问题,那么,生活中还有哪些问题也可以用这样的方法来解决呢?
课件出示:
师:这是挖隧道问题,可以用画图的方法来解决吗?
师:其实生活还有很多问题,比如两个人跳绳、两个人打字等问题都可以用这样的方法来解决。
课件出示:
【评析】在课堂结束环节揭题,其实就是让学生在慢慢解决问题的过程中,逐步渗透扩充相遇问题的模型,促使学生有效地理解。把相遇问题的方法迁移到生活中的其他速度类问题,有效沟通了不同习题之间的联系,使得学生再次感悟“速度和×时间=总数”这种模型,也为今后学生解决这类问题打下基础,有效提升学生解决问题的能力。
虽然“相遇问题”并非四年级数学教材内容,但教师要善于整合教材资源,合理设计内容来提升解决问题教学的质量。解决问题本身也是帮助学生感悟模型思想的主要途径之一,随着课程改革的深入,越来越多的教师关注数学思想的感悟与运用,因此,教师在解决数学问题的教学中要善于收集、整理、对比和运用材料,通过对比、沟通和迁移感悟解决问题的变与不变,有效提升学生解决问题的能力。
注:本文作者参加2019年杭州市小学数学课堂教学观摩评比活动中荣获一等奖。
【作者简介】孔忠伟(1984— ),浙江杭州人,大学本科学历,高级教师,区兼职教研员,区名师导航站站长,研究方向为小学数学教学。
(责编 杨 春)

