螺杆转子砂带磨削装置开发及材料去除率预测
杨赫然 何 源 孙兴伟 董祉序 乔赫廷
1.沈阳工业大学机械工程学院,沈阳,1108702.辽宁省复杂曲面数控制造技术重点实验室,沈阳,110870
0 引言
螺杆转子作为螺杆泵、压缩机等螺杆机械产品的核心部件,其加工质量直接决定自身乃至整个系统的使用寿命。螺杆转子类零件加工制造的最后一步为磨削,磨削的去除均匀性直接决定转子的加工质量,因此改善螺杆转子表面磨削的去除均匀性成为提高螺杆机械性能的关键技术之一[1]。
砂带磨削因具有冷态和柔性两个特征,在加工曲面时贴合性强、散热性好,被广泛应用于螺杆转子的精密加工中。若磨削过程中,工件表面材料磨削去除深度差异较大,会很大程度上影响工件表面的型面精度,因此,实现工件表面磨削时的均匀去除成为首要的研究目标。目前的研究中,通常先考虑磨粒和工件表面的相互作用原理,然后建立磨削去除模型,预测和分析不同磨削工艺参数下加工工件表面材料去除率,最终根据需要的材料去除率对工艺参数进行规划。影响磨削材料去除率的主要因素为接触区域的接触应力、磨削速度及磨料目数等,且各因素之间存在耦合,很多学者通过理论分析或实验的方式开展了深入的研究。王品章[2]围绕飞机叶片类零件的磨削加工进行研究,针对不同接触方式,利用Hertz 接触理论建立了叶片在砂带恒力磨削过程中的法向接触应力分析模型;ZHE等[3]基于Preston 方程及Hertz 接触理论预测了去除深度的廓形。孙聪等[4]在考虑磨粒尺寸、分布位置的前提下,提出了工件表面的材料去除率模型;PANDIYAN 等[5]基于自适应模糊神经推理理论提出了砂带磨削深度预测模型;张广鹏等[6]利用磨削时产生的火花图像信息,改进了砂带磨削材料去除率预测模型;商维等[7]基于虚拟格子法建立了虚拟砂轮模型,并对磨削去除量进行了分析;BAI等[8]采用模拟分析与理论模型相结合的研究方式,总结出了锋利的磨粒易获得较高材料去除率的规律。
综上所述,为实现工件表面磨削时去除均匀,许多学者开展了接触应力分布及材料去除率预测的理论分析、数值与实验仿真研究,但是研究对象多以平面磨削、点磨削等定曲率轨迹为主,或针对局部磨削去除的分析,面向螺杆转子等具有螺旋曲面工件的研究较少。此外,对螺旋曲面类工件进行磨削加工,磨削工具沿工件截面型线进给时,工件与磨削装置的接触区域的曲率随着加工运动将发生显著变化,从而导致去除区域接触应力波动较大,增大了工件表面均匀去除的难度。
本文以复杂螺杆转子表面的磨削加工为对象,以实现均匀去除为目标,开展了装置设计与预测算法的研究。首先,根据螺杆转子型面特征开发接触轮式与自由式两种砂带磨削装置,实现不同曲率处曲面的同步磨削加工,在加工螺杆转子时,可沿轴向同时布置多套装置,实现不同曲率处曲面的同步磨削加工;然后,本文根据磨削装置与工件的接触特点建立各自的接触应力分布模型;鉴于ThunderGBM算法具有独特的内存池、高速的RLE(run length encoding)行程压缩等特点,适用于解决回归问题、多分类问题和排序问题[9],提出基于ThunderGBM算法的材料去除率预测模型;最后,采用磨削实验对所提出的预测模型进行验证。
1 螺杆砂带磨削装置开发
本文的研究逻辑框图见图1。螺杆转子为典型的螺旋曲面类零件,其截面轮廓一般由多段曲线连接构成,其中五头螺杆转子的截面型线如图2所示。图2中AB段为顶端部分轮廓截面型线,CD段为底端部分轮廓截面型线,BC段为顶部和底部连接段轮廓截面型线。

图1 研究逻辑框图Fig.1 Block diagram of research logic

图2 五头螺杆转子截面型线示意图Fig.2 Sectional profile diagram of five head screw rotor
由于螺杆转子不同轮廓处曲面的曲率不同,为达到均匀去除的目的,可针对各部分轮廓采用与其型面特点相适应的磨削方式。由于AB段表面凸起,易于与砂带表面进行贴合,适宜利用自由式砂带磨削方式进行加工,而BC段与CD段的凹形曲面区域则比较适用接触轮式砂带磨削方式,因此,本文开发接触轮式砂带磨削装置和自由式砂带式磨削装置对螺杆转子不同部分曲面进行加工。磨削装置模型如图3所示。
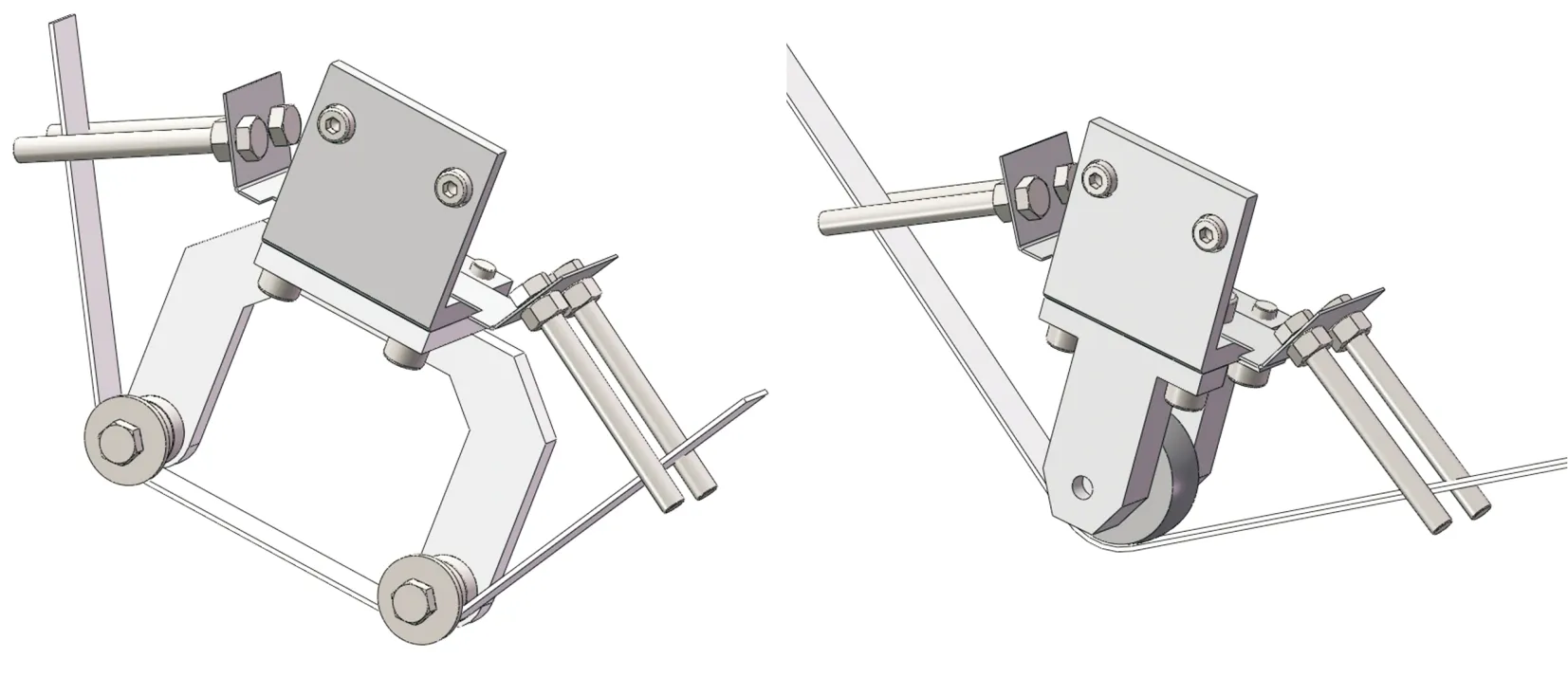
(a)自由式砂带磨削装置 (b)接触轮式砂带磨削装置图3 自由式和接触轮式砂带磨削装置示意图Fig.3 Schematic diagram of free and contact wheel belt grinding mechanism
将图3所示的磨削装置搭建于数控车床上,利用数控车床的主轴运动及溜板运动实现工件回转及磨削装置沿工件的轴向进给运动。
磨削装置搭建完成后,首先需建立坐标系。本文分别建立工件与磨削装置的全局坐标系、工件局部接触区域处的局部坐标系以及磨削装置位置的刀具坐标系,如图4所示。机床坐标系以OmXmYmZm表示,其中,Zm轴与车床主轴轴线共线且指向床尾;Xm轴竖直向上,原点Om位于工件装夹处的工件端面上。工件坐标系以OwXwYwZw表示,其中原点Ow与机床坐标系原点Om重合,Zw轴与Zm轴重合,Xw轴与Xm轴相差φ角。刀具坐标系以OtXtYtZt表示,其中原点Ot位于Zm轴上,OtOm之间的距离设为λ,Xt轴垂直于主动轮端面并与Zm轴相差β角,Zt轴平行于主气缸活塞运动方向,并指向主气缸末端。局部坐标系用OlXlYlZl表示,其原点Ol与Ot重合,Zl轴与Zt轴重合,Xl轴与工件坐标系Zw轴平行。
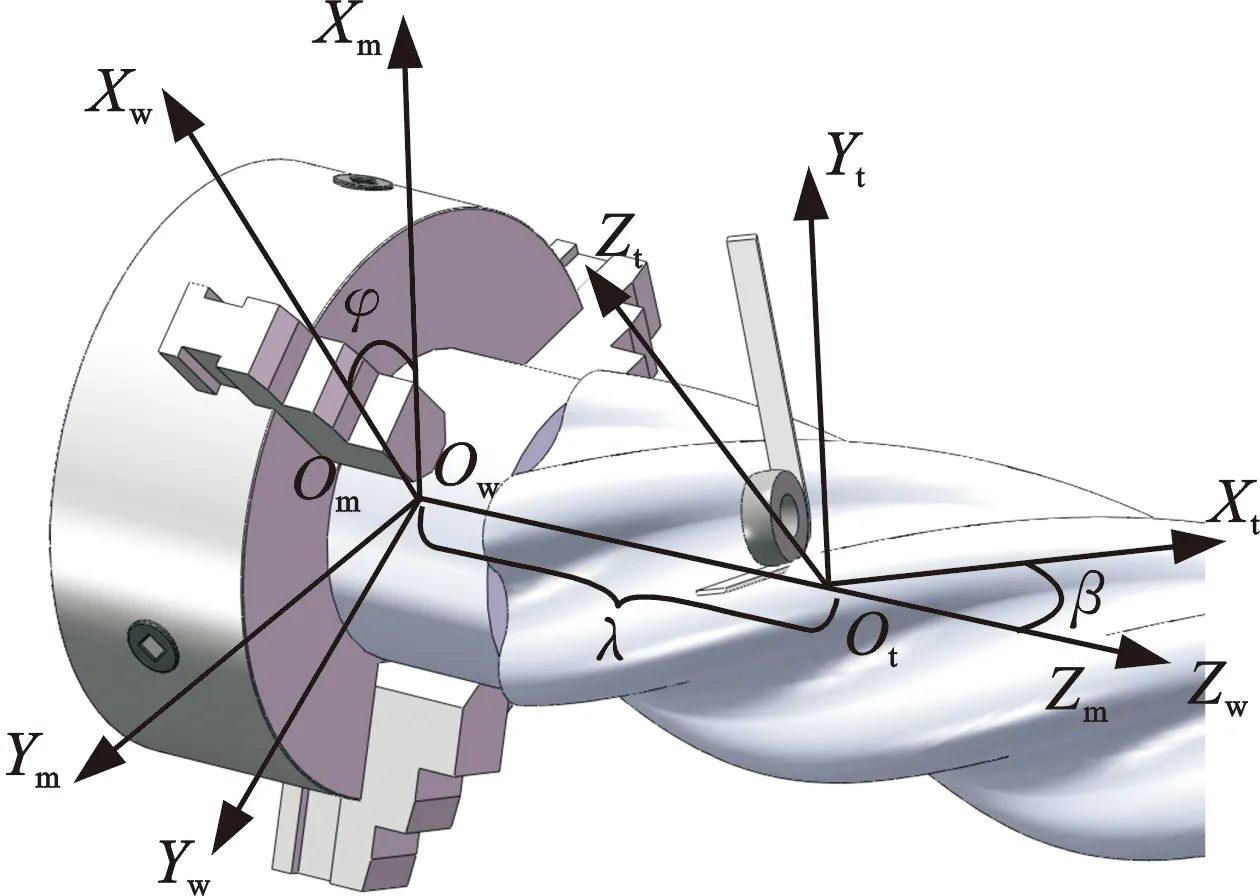
图4 磨削加工坐标系Fig.4 Grinding coordinate system
2 砂带与工件的接触模型
2.1 基于半解析法的接触轮与工件接触模型
对单次磨削加工而言,影响复杂曲面砂带磨削材料去除率的主要因素中,砂带线速度与砂带目数为确定的工艺参数,而接触应力会随着接触区域曲率的变化而变化,接触应力直接影响磨粒切入材料的深度,从而影响材料去除率。简而言之,接触应力分布规律的研究对材料去除率预测至关重要,且接触模型是接触应力分析的基础,因此选择合适的接触模型成为本文研究工作的首要任务。
建立接触模型之前,首先需对本文研究对象作简化处理。本文采用接触轮式磨削装置对螺杆转子进行加工时,由于砂带的基材、黏结剂及磨料等在接触法向上的弹性变形微小,因此砂带的变形量可以忽略不计,据此得到磨削装置与工件接触时所产生的接触应力与接触区域可以近似等效为接触轮与工件直接接触所产生的接触应力与接触区域。
半解析法是基于弹性力学的接触分析方法,应用范围较广,且具有计算简便、容易收敛等特点,适用于解决复杂曲面之间的弹性及弹塑性接触问题[10-11],因此本文基于半解析法建立接触轮与工件的接触模型,并利用数值解析法对其进行求解,获得接触区域内各节点处的接触应力数值。
根据工件截面型线及实际加工条件,模型相关参数设置如下:螺杆转子材料为45钢,其弹性模量及泊松比分别为210 GPa和0.28;接触轮材料为橡胶,直径为30 mm,弹性模量及泊松比分别为1 GPa和0.45。数值法求解时,网格划分尺寸为0.1 mm×0.1 mm,主气缸输出压力为80 N。由以上条件可以得到接触区域各节点处的接触应力值。根据模型计算结果可绘制出接触轮与工件的接触应力云图,如图5所示。由图5可知,接触区域内的最大接触应力约为0.8 MPa,最小应力约为0.3 MPa,同时可以看出接触区域应力分布连续,接触轮两侧面处的应力边界较为清晰,接触轮未覆盖的区域应力值为0,计算结果准确合理。
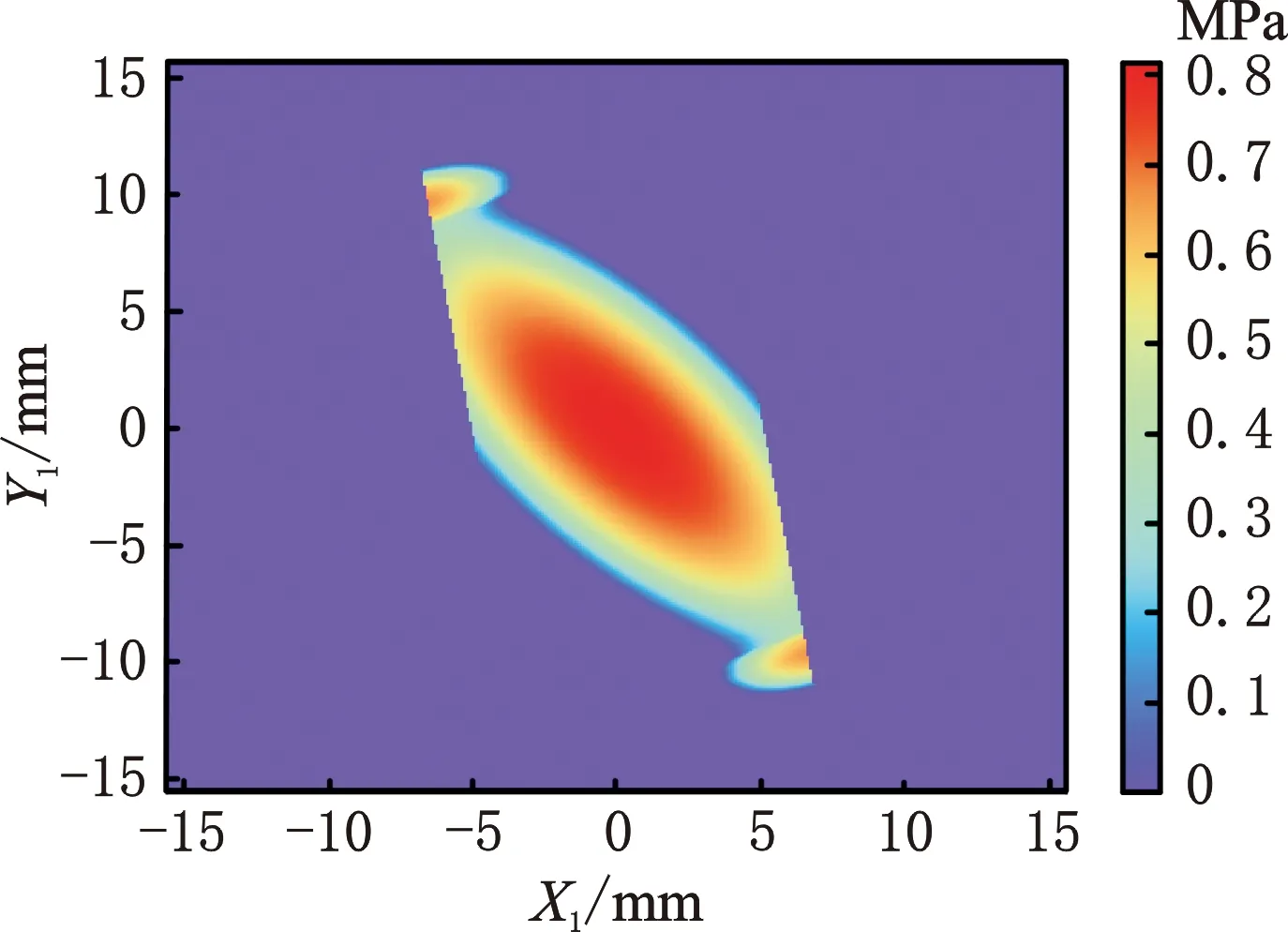
图5 接触轮与工件的接触应力云图Fig.5 Cloud chart of contact stress between contact wheel and workpiece
2.2 基于几何近似法的自由式砂带与工件接触模型
自由式砂带磨削装置对螺杆AB段转子进行加工时,导轮之间的砂带在张紧力的作用下紧绷。由于砂带在此状态下仅产生几何变形,因此本文采用几何近似法对其接触应力进行分析。此时接触区域为砂带所包覆的螺杆转子截面顶部区域,砂带与螺杆转子接触时会形成图6所示的接触接合线。

图6 接触接合线示意图Fig.6 Schematic diagram of contact joint line
设总下压力为F0,该值由磨削系统主动气缸进行控制,则该区域内正应力分布可近似为pz,pz可由下式计算得出:
(1)
式中,St为由砂带边界线与接触接合线所围成的接触区域面积。
为了简化求解过程,接触区域面积St可在刀具坐标系下通过积分得出:
(2)
在实验加工中,砂带宽度b=10 mm,下压量h=12.16 mm,导轮中心距离lt=35 mm。利用式(2)及实验参数可得接触区域面积St为104.29 mm2,则由式(1)可知正应力pz为0.86 MPa。由此可求得接合线坐标计算值,列于表1。
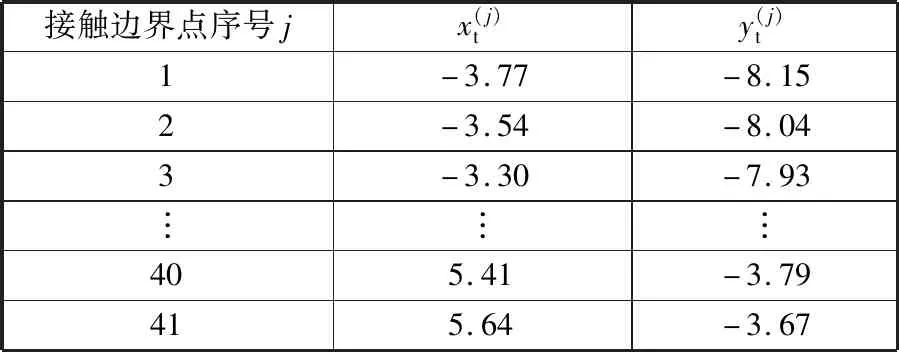
表1 接触边界点计算值Tab.1 Calculated value of contact boundary point mm
为初步验证算法的计算精度,采用有限元法针对转子自由式砂带磨削进行接触分析。按照实验条件设置参数,基于有限元分析得到接触应力分布云图见图7。从图7所示的应力云图中可以看出,接触区域的中心位置应力值较大,为0.98 MPa,中心区域之外应力值约为0.5 MPa,分布较为均匀。

图7 自由式砂带磨削装置有限元接触应力云图Fig.7 Finite element contact stress nephogram of free belt grinding mechanism
将基于有限元计算得出的接触区域与仿真接触区域进行对比,如图8所示。由图8可知,使用几何近似法与有限元法所得到的接触区域形状均为多边形,二者接触区域重叠面积约为88%。此外,由于有限元仿真过程中考虑工件的弹性变形,因此几何近似法计算的区域面积会略小于有限元法仿真所得的区域面积,故本文的计算结果合理。
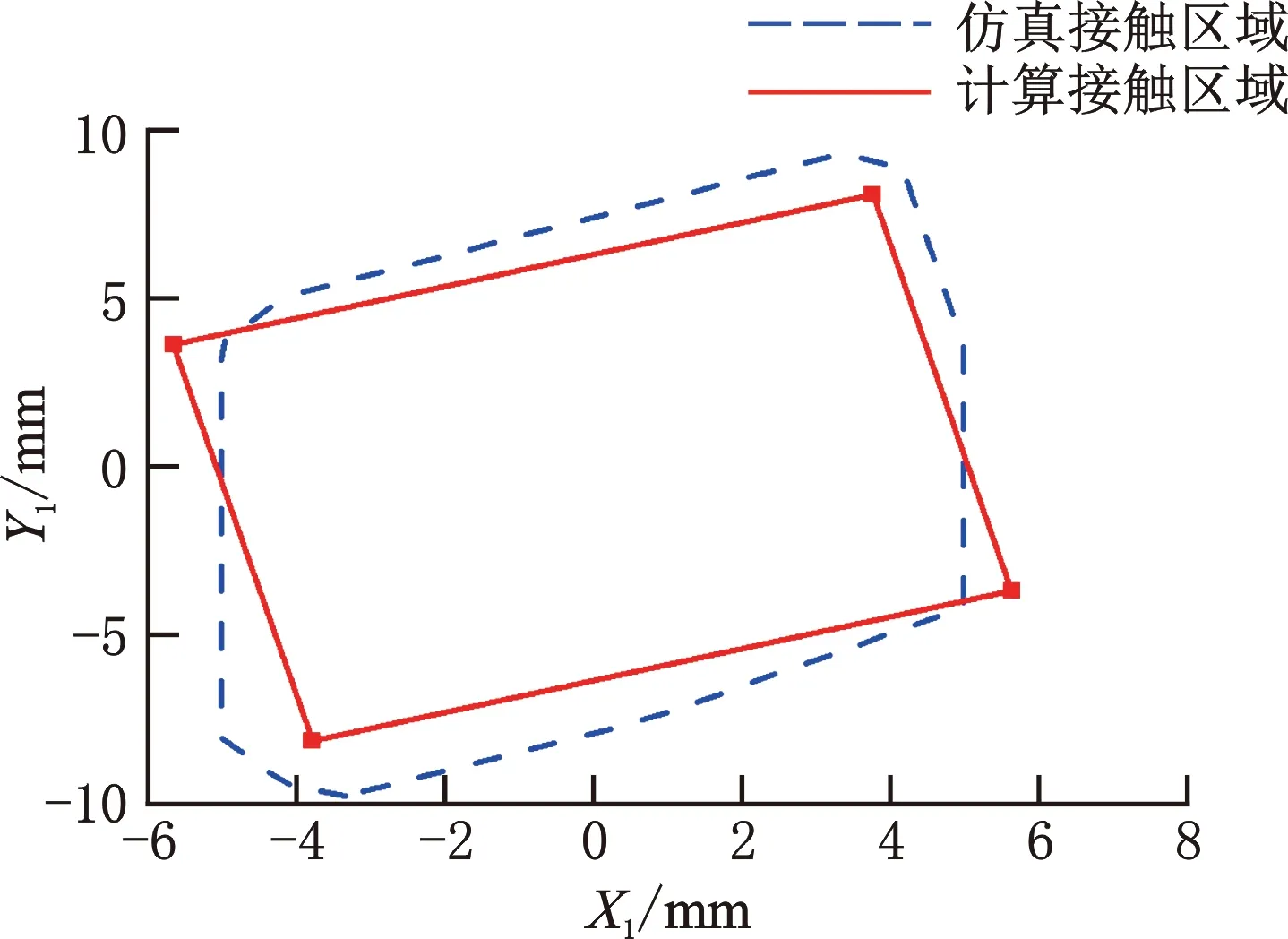
图8 几何近似法与仿真法得到的接触区域对比Fig.8 Comparison between geometric approximation method and simulation method contact area
通过计算结果的对比可知,几何近似法计算所得接触区域可以较准确地反映该类接触问题的真实接触区域形状。
3 基于ThunderGBM的材料去除率预测模型
在获得砂带与工件接触区域的接触应力分布规律后,本文提出基于ThunderGBM算法的材料去除率预测模型,ThunderGBM模型的预测值由下面的预测模型函数计算得出:
(3)
(4)
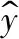
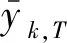
(5)
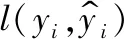
当解决回归问题时,损失函数通常选择均方误差函数,即
(6)
在ThunderGBM模型中,满足以上最优问题的分隔点也满足所计算的增益g为最大,增益g可以由下式获得:
(7)
(8)
式中,GL、GR分别为左右节点的梯度gi的和;HL、HR分别为左右节点的二阶导数hi的和。
在预测阶段,ThunderGBM模型将预测任务和树模型以并行计算的方式进行遍历。具体过程如下:
从拟建/在建和储备项目总量来看,近期最为活跃的长青集团在2015~2016年大举扩张,累计签署32个秸秆直燃发电项目的投资合作框架协议,拟装机规模1355MW。目前其河南方城、辽宁灯塔、山东曹县等13个秸秆直燃发电项目已签署投资协议,山东鄄城项目获得核准[27]。
(1)在数据预处理过程中去除异常点,以防止影响拟合结果。在去除完成后,将样本集合切分成训练集和测试集,一般训练集约占总数据量的80%。为避免由于数据切分不合理造成的过拟合,可以利用交叉验证的方法进行多次训练和测试。
(2)在并行计算过程中,ThunderGBM模型首先对数据集结构进行优化,由原本的矩阵型训练集数据转为剔除0值之后的键值对型结构;然后采用行程编码压缩技术将训练样本数据进行压缩,以加快在计算机总线中的传输速度;最后将压缩的数据放到内存池中,并行计算这些数据以构建树模型。
(3)构建树模型。ThunderGBM模型的树模型构建阶段首先需要给定目标模型树的数量、深度和增益阈值。对于每一棵模型树,均由一根节点开始,根节点包含全部的样本,在每一次节点遍历中,均需对所有特征属性进行遍历。在本预测模型中,特征参数是砂带目数、接触应力和砂带线速度[12]。
本文在训练集构建阶段采用单点分组实验法对多组加工参数进行实验仿真,并以磨削材料去除率作为模型训练的目标函数。为了获得工件表面上参与磨削加工的数据点集,需要利用实验前划定的实验区域位置进行数据提取。实验区域内部用来进行定点磨削加工实验,对于某一位置上的测量点,该点处的接触应力由2.1节及2.2节所述步骤根据接触区域型面及施加的气缸压力等实验条件进行计算得出,以向量形式作为预测模型的输入参数,而砂带线速度及砂带目数等磨削工艺参数在单次加工中为恒定值。
根据文中预测对象,单位时间法向磨削深度即为材料去除率r,可由实验测得的磨削深度与驻留时间获得:
(9)
式中,z′为工件表面磨削深度,t′为在该位置的驻留时间。
ThunderGBM预测模型的输入样本矩阵为
(10)
式中,Ni为砂带目数;pi为局部接触应力;vsi为砂带线速度。
预测输出结果为下式所示的n维列向量:
Y=(r1,r2,r3,…,rn)T
(11)
其中,rn为第n组数据的材料去除率,可根据式(9)计算得出。
训练结束后,即可进行磨削材料去除率的预测。以砂带磨粒粒度d、局部接触应力p和砂带线速度vs等参数为输入,利用ThunderGBM预测模型即可得到该处的磨削材料去除率。材料去除率在抛光加工中定义为单位时间内工件厚度在抛光前后的变化值,结合本文情况,以单位时间法向磨削去除深度进行表征。获得材料去除率后,可进一步得到砂带磨削装置在Zm向运动速度为vz的情况下,螺杆转子表面各处去除深度
(12)
式中,L为磨削装置与工件在相对运动时包络形成的螺旋线。
4 实验验证
4.1 材料去除率预测
为完成转子表面磨削材料去除率预测模型的训练,本文采用定点加工实验进行数据采集。定点实验中,在工件表面不同区域处使用不同的加工参数进行磨削加工实验。根据工件表面轮廓曲率以及磨削加工原理,将工件轮廓分为图2 中的AB、BC、CD3个区域,并在这些部位上设计多组磨削实验。本实验装置整体结构如图9所示,其中,1为数控机床本体;2为五头螺杆转子,材料为45钢,大径为112.8 mm,小径为79.8 mm,导程为650 mm;3为基恩士LK-H080激光位移传感器;4为磨削装置。在加工时,将待加工工件装夹到车床三爪卡盘上,并调整磨削装置各工具的相位,保证磨削头对准所要加工的区域。

1.机床 2.工件 3.激光传感器 4.磨削装置 5.气缸图9 实验装置示意图Fig.9 Schematic diagram of experimental device
实验中,影响磨削材料去除率的主要因素为气缸输出压力F,砂带线速度vs及磨削停留时间t。根据以上工艺参数设计单变量实验组作为训练编组,部分实验参数列于表2。其中,AB区域的实验组使用自由式砂带磨削方式进行加工,F为张紧气缸输出压力,BC和CD区域使用接触轮式磨削方式。

表2 单变量定点加工实验部分实验分组表Tab.2 Experimental grouping table of single variable fixed point machining experiment
为了验证本文所提出算法的有效性,将计算结果与预测模型所得结果进行对比,其中部分训练数据如表3所示。为验证算法的有效性,利用评价函数对算法进行评判,常见评价参数有可决系数R2、模型训练时间和均方误差(σMSE)等,计算公式如下:
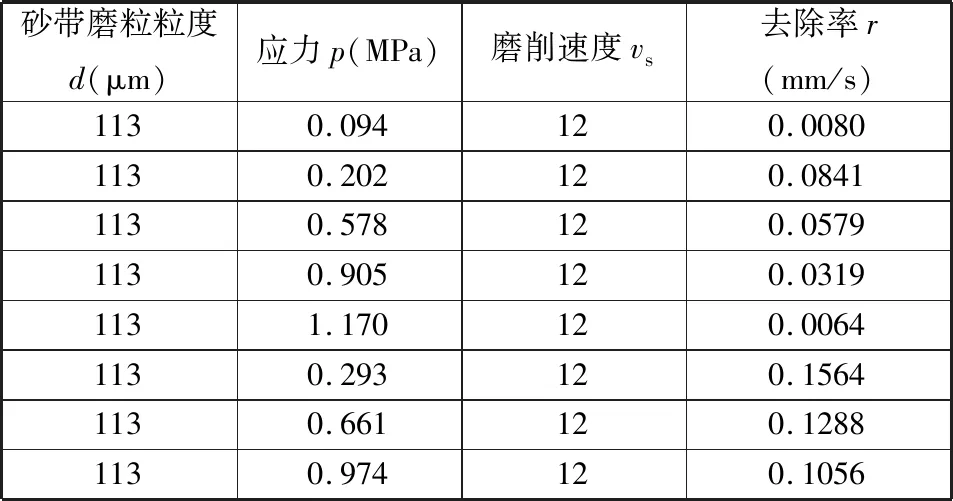
表3 部分训练数据Tab.3 Partial training data
(13)
(14)
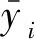
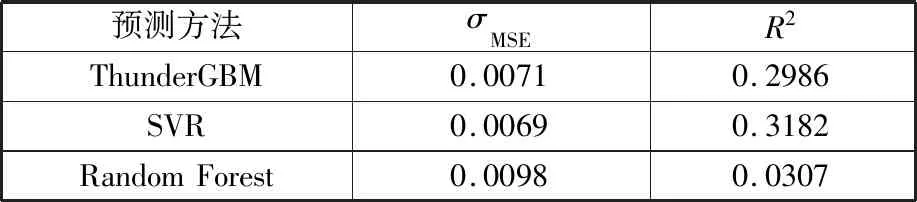
表4 预测精度评价参数对比结果Tab.4 Comparison results of prediction accuracy evaluation parameters
根据表4的结果,ThunderGBM在模型准确度方面与SVR预测准确度相当。训练时间方面,针对105个样本展开训练,各算法耗时情况如表5所示。可以看出,ThunderGBM在大数据量情况下的模型训练速度要明显优于SVR训练速度。从训练精度和训练速度两方面综合考虑,基于ThunderGBM的预测模型具有一定的优势。
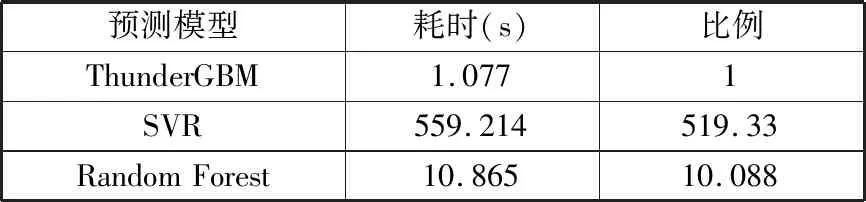
表5 预测耗时对比结果Tab.5 Comparison results of forecast time-consuming
4.2 螺杆转子联动磨削实验

(15)
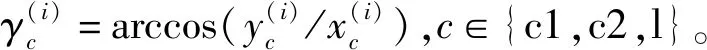
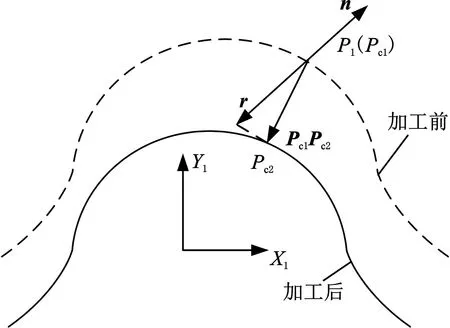
图10 法向磨削深度几何关系示意图Fig.10 Geometric relationship of normal grinding depth
联动磨削加工时,工件绕Zw轴转动,砂带在主动轮的带动下高速运动,同时磨削装置沿着Zw轴进给。联动磨削中部分加工参数如下:
(1)磨削螺杆AB段曲面时,使用张紧力为40 N,砂带速度为12 000 mm/s,主气缸压力为最大值(气缸行程达到机械限位),砂带磨粒粒度为113 μm,进给速率为300 mm/min。
(2)磨削螺杆BC段曲面时,使用张紧力为20 N,砂带速度为12 000 mm/s,主气缸压力为40 N,砂带磨粒粒度为113 μm,进给速率为300 mm/min。
(3)磨削螺杆CD段曲面时,使用张紧力为20 N,砂带速度为12 000 mm/s,主气缸压力为80 N,砂带磨粒粒度为113 μm,进给速率为300 mm/min。
通过将理论预测的磨削深度曲线与联动磨削实验中实际测得的数据相对比,可得到图11所示的表面轮廓整体对比结果。
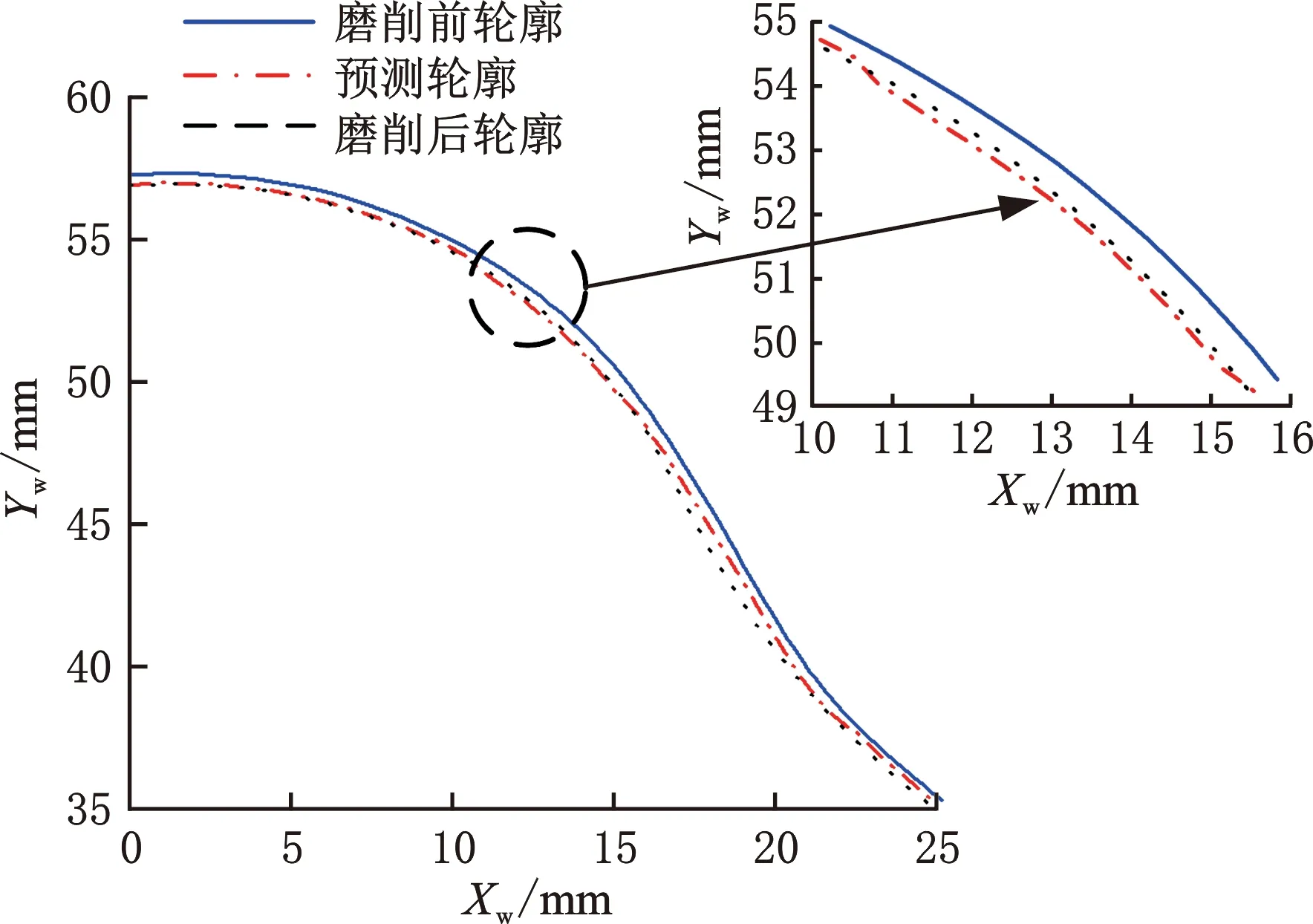
图11 预测数据与实测结果对比图Fig.11 Comparison between predicted data and measured results
图12所示为实验与预测模型计算法关于法向磨削去除深度对比结果,可以看出预测值与实验测量值具有较高的一致性,平均误差仅约为0.01 mm,最大误差值不超过0.0296 mm,可见对于本文研究对象来说预测模型具有较高的精度。联动磨削过程中,通过工件旋转与磨削装置轴向直线的插补运动,实现接触轮及自由砂带始终与各自的加工表面紧密贴合,并可以保持接触区域总压力恒定。由于受到待加工工件表面廓形影响,接触区域内工具与工件之间的接触压力会有一定的波动,然而由实验结果可知,影响较小。
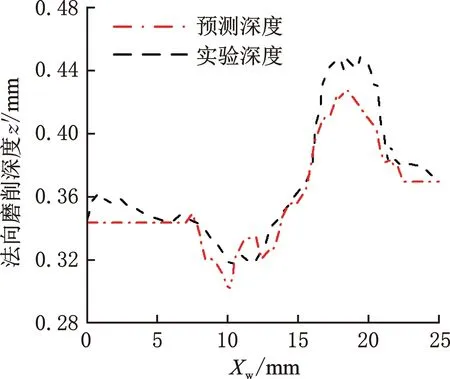
图12 去除深度对比图Fig.12 Comparison chart of remove depth
由图11可以看出,基于本文提出的预测模型计算出的预测廓形与实际加工后测量廓形无论形状与数值均具有较高的重合度。法向去除深度非均匀性参照WIWNU(片内非均匀性)进行计算,根据测量值,法向去除深度非均匀性约为7%,表明本文开发的磨削装置与加工方法能够实现螺杆转子表面的均匀去除。
上述工作表明了本文所提出的预测模型的有效性,可为实际工程提供准确的分析方法。进一步研究了实际加工中比较关心的接触应力与材料去除率之间的规律,图13是砂带线速度12 m/s、砂带磨粒粒度113 μm时利用预测模型得到的接触应力对材料去除率影响曲线,可以看出,随着接触应力增大,磨粒切入材料深度增加,从而使材料去除率增大;当接触应力处于0.5~0.8 MPa时,接触应力变化对材料去除率影响趋势变平缓,主要是由于接触应力增大引起的磨粒切入深度并没有使工件表面材料产生塑性形变并产生磨屑,因此没有产生实际去除;而当接触应力大于0.8 MPa时,接触应力的增大对材料去除率的影响较为明显,且接近线性变化。

图13 接触应力对材料去除率影响Fig.13 Effect of contact stress on material removal rate
5 结论
(1)针对螺杆转子曲面特点,开发了专用磨削装置,以实现高效的均匀去除;分别对接触轮式与自由式两种砂带磨削装置在磨削加工时的接触问题进行了建模分析,利用半解析法和几何近似法建立了接触模型,得到了两类问题的接触应力分布规律。
(2)通过对磨削去除理论研究,提出了基于ThunderGBM算法的螺杆转子表面磨削材料去除预测模型。通过磨削实验,验证了本文所提出的相关方法的正确性。本文所提出的材料去除率预测模型可以为螺旋曲面类工件的砂带磨削过程中的均匀去除提供理论指导,开发的磨削装置可以实现螺杆转子表面的均匀去除,用于螺杆的精密加工。

