磁流变液与电热形状记忆合金联合传动性能研究
熊 洋 黄 金 舒锐志
重庆理工大学机械工程学院,重庆,400054
0 引言
磁流变液(magnetorheological fluid,MRF)是一种形态和性能受外加磁场约束和控制的固液两相智能材料,其优异的性能表现为在外部磁场的作用下,磁流变流体在毫秒间完成从液态到接近固态的可逆转变[1]。在磁感应强度增大过程中,这些流体的表观黏度可以表现出数量级的变化,也表现出类似固体的力学性质,具有一定的剪切屈服强度,并且可由外加磁场连续控制[2-3]。形状记忆合金(shape memory alloy,SMA)是一类具有形状记忆效应和超弹性的新型智能合金材料[4],该材料在不同的温度下具有不同的晶体结构。SMA被加热超过一定温度就会开始由非孪晶马氏体向奥氏体转变,宏观上表现为恢复到原来的形状[5]。
由于MRF在磁场作用下产生的剪切屈服应力较小,因此大多数学者基于MRF剪切模式提出的圆盘式或圆筒式传动装置所产生的转矩偏小,制约了MRF传动装置在工业中的应用。为了增大MRF传动装置的转矩,将圆盘式改进为多盘式,如WU等[6]设计的一种多盘式大功率MRF传输装置可产生1880 N·m的最大输出转矩;将圆筒式改进为叠筒式,如QIN等[7]采用的一种新颖的多滚筒结构,在有限的体积内激活了更多的剪切区域,提高了MRF传动装置性能;将MRF剪切与挤压相结合,如WANG等[8]设计了一种挤压剪切模式下的MRF制动器,实验样机的测试结果表明,在大电流、高压应力、大压缩应变和小初始间隙下,该制动器可以产生较大的转矩。但是圆盘式改进为多盘式、圆筒式改进为叠筒式均无法避免地会使传动装置发热严重并导致MRF性能衰减,WANG等[9]通过试验得出多盘式制动器发热可导致传递转矩减小50%;MRF剪切与挤压相结合对零件精度和密封要求极高,ZHANG等[10]通过试验得出当挤压应力达到1.5 MPa时,传动装置转矩才有明显增大。
以上对MRF传动装置性能提升的研究仅限于磁流变液剪切模式和挤压模式,特别是在MRF传动装置性能提升的研究中,大多未解决结构堆叠导致发热严重、液体高压导致密封要求高的问题。笔者所在团队通过将SMA弹簧加入MRF传动装置,实现了传动装置输出转矩的智能控制、传动装置输出转矩的提高,如黄金等[11]提出的热效应下SMA驱动的MRF摩擦复合传动方法可保持装置高温下传动的稳定性;乔臻等[12]采用SMA弹簧使得装置能够根据环境温度自动控制输出转矩;王西等[13]提出的圆锥式MRF与SMA复合传动方法,在高温下SMA可以弥补MRF性能下降的缺陷,比传统圆盘MRF传递的转矩更大;黄金等[14]通过温控SMA弹簧来驱动MRF,使MRF的工作间隙由一面变为两面,增大了装置所能传递的转矩。本文在以上工作的基础上针对磁流变液装置所产生的转矩偏小的问题,提出了一种MRF与电热SMA联合的传动方法,通过理论分析与实验为MRF与电热SMA联合传动装置设计与制造提供依据。
1 工作原理
MRF与电热SMA联合传动装置结构如图1所示,装置由电热SMA弹簧、调整螺钉、复位弹簧、输入轴、导杆、螺塞、摩擦盘、励磁线圈、隔磁环、输出轴、电滑环、壳体和MRF等组成。其中主动盘凸缘与左壳体凹槽之间的1 mm缝隙为MRF工作区域。传动装置的工作原理如下:

(a)二维剖视图
(1)初始状态下,输入轴在外源动力牵引下进行回转运动;电热SMA弹簧未通电流不产生压力,摩擦盘与主动盘之间保持0.5 mm初始间隙;励磁线圈也未通电流,MRF表现为牛顿流体状态,所产生的黏性转矩极小,依靠MRF的黏性转矩不能带动从动件转动。此时传动装置处于脱开的状态。
(2)电热SMA弹簧通入电流产生热量,温度达到SMA相变临界温度时弹簧输出压力推动摩擦盘挤压主动盘,从而产生摩擦转矩,同时励磁线圈也通电,磁通穿过MRF的工作间隙,MRF中的磁性颗粒沿磁通方向排列成链状结构,产生较大的剪切屈服应力,依靠此应力能传递转矩,装置在摩擦与磁流变联合作用下传动转矩显著增大。此时传动装置处于接合的状态。
(3)励磁线圈断电,MRF又恢复为牛顿流体状态;同时电热SMA弹簧也断电,弹簧中的热量消失,复位弹簧拉回摩擦盘,摩擦盘与主动盘脱离接触,压紧力消失。此时传动装置恢复为初始的脱开状态。
2 传动装置转矩特性分析
2.1 摩擦转矩
SMA在相变过程中,弹簧的变形受到约束,则弹簧会对约束体产生作用力,这个力为回复力,用Fr表示。SMA的回复力与环境温度和受约束的变形量密切相关。
当SMA的温度处于Mf与Af(Mf为马氏体相变结束温度,Af为奥氏体相变结束温度)之间时,在温度的驱动下弹簧的回复力为[15]
(1)
式中,δ(θ)为弹簧的轴向伸缩量,该伸缩量是关于温度的函数;G(θ)为SMA剪切模量,该剪切模量是关于温度的函数;δL为温度低于奥氏体相变开始温度As时的轴向伸缩量;GL为温度低于As时的SMA剪切模量。
进一步地,低温下SMA弹簧的轴向载荷为
(2)
式中,D为弹簧中径;d为SMA丝的直径;n为有效匝数。
当约束SMA弹簧的轴向位移时,弹簧的轴向伸缩量不变,即δ(θ)=δL。由式(1)、式(2)可知,当SMA的温度处于Mf与Af之间时,在温度的驱动下弹簧的回复力Fr为
(3)
如图1所示,传动装置中的摩擦盘为圆环状,其中圆环的内径为r1、外径为r2。摩擦盘在SMA弹簧回复力Fr的作用下与主动盘挤压摩擦,则摩擦盘上的应力σ为
(4)
取到摩擦盘圆心距离为r的微元环,微圆环的宽度为dr,则微元环的面积dS为
dS=2πrdr=πdr2
(5)
进一步,该微元环所产生的摩擦转矩为
(6)
式中,μ为摩擦盘接触面的摩擦因数,该摩擦盘为干式摩擦副,μ取0.204~0.222[16]。
对式(6)积分,积分限为内径r1到外径r2,可得出N个SMA弹簧产生的摩擦转矩Mf为
(7)
以2、4、8个电热SMA弹簧挤压摩擦盘产生摩擦转矩Mf为例,摩擦盘内径r1=38 mm,外径r2=70 mm。设摩擦盘的摩擦因数μ为0.21,SMA弹簧的结构参数为:弹簧中径D=8.6 mm,SMA丝的直径d=1 mm,有效匝数为6,倾角α=6°。SMA奥氏体相变开始温度As与奥氏体相变结束温度As分别为63.28 ℃和92.91 ℃,奥氏体剪切模量GA与马氏体剪切模量GM分别为13.8 GPa和8.0 GPa。将各个参数代入式(7)中,可以得出2、4、8个电热SMA弹簧挤压摩擦盘所产生的摩擦转矩Mf,计算结果如图2所示。

图2 不同SMA弹簧个数产生的摩擦转矩Fig.2 Friction torque versus different numbers of SMA springs
由图2可知,2、4、8个电热SMA弹簧产生的最大摩擦转矩Mf分别为0.225 N·m、0.899 N·m和1.798 N·m。电热SMA弹簧温度从60 ℃升高到75 ℃,产生的摩擦转矩缓慢地增大,从75 ℃升高到93 ℃,产生的摩擦转矩快速地增大,从93 ℃升高到100 ℃,产生的摩擦转矩又缓慢地增大,当温度超过100 ℃后,产生的摩擦转矩不再增大。由式(7)可知,摩擦转矩Mf与电热SMA弹簧个数成线性增长关系。
2.2 磁流变液转矩
磁场的磁路应当使MRF磁化方向与制动装置剪切流动方向垂直,并且尽可能地使MRF工作间隙为高强度磁场。为进行传动装置结构的磁场分析,简化磁场分析模型,如图3所示。

图3 磁场分析简化模型Fig.3 Simplified model for magnetic field analysis
MRF的型号为MRF-132DG,材料属性如图4所示。传动装置左外壳和右外壳材料均为KTH300-10铸铁,输入轴材料为Q235碳素结构钢,隔磁环的材料为铜,其中KTH300-10和Q235磁性曲线见图5。

图4 MRF-132DG材料属性Fig.4 MRF-132DG material properties

图5 KTH300-10和Q235磁性曲线Fig.5 Magnetic curves of KTH300-10 and Q235
根据传动装置的设计要求,磁场分析模型的尺寸参数如下:R1=60 mm,R2=45 mm,R3=43 mm,R4=35 mm,L1=16 mm,L2=8 mm,L3=10 mm,L4=1 mm。
磁场设置为轴对称稳态磁场,材料属性按图4和图5定义,设置为Neumann边界条件,激励定义为电流I=1 A,励磁线圈的匝数n=380,完成设定后求解计算。磁感应强度求解结果如图6所示。

图6 磁感应强度分布与磁力线Fig.6 Distribution of magnetic induction intensity and magnetic force line
由图6中磁感应强度分布图可以观察到MRF间隙的磁感应强度最大值位于工作区域中部,大小为1.02 T,MRF间隙的磁感应强度最小值位于工作区域底部,大小为0.45 T。通过分析可知:当激励电流为1 A、线圈匝数为380时,最大值接近但未超过MRF的磁饱和强度,磁力线均匀地环绕线圈形成回路,并且垂直地穿过了MRF工作间隙。这些都说明传动装置进行了合理的结构设计和材料选择。
MRF剪切面径向磁场强度变化规律如图7所示。MRF工作间隙磁场强度沿着半径增大的方向从89.19 kA/m增加达到峰值311.60 kA/m,随后减小到224.50 kA/m。
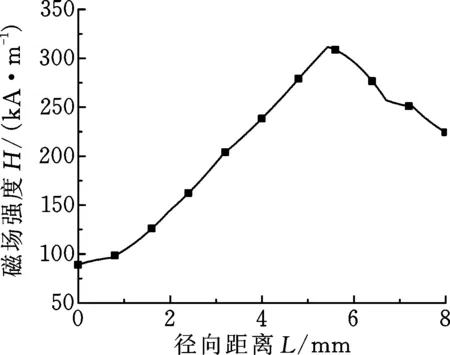
图7 径向磁场强度变化规律Fig.7 Variation of radial magnetic field intensity
圆环状MRF剪切示意图见图8,圆环内径为R4、外径为R3。主动轴以角速度为ω1进行旋转,由MRF剪切力所产生的转矩驱动从动轴以角速度ω2进行旋转。假设工作间隙中的MRF在磁场作用下全部屈服做剪切流动,MRF传递的转矩为[17]

图8 磁流变液圆环剪切示意图Fig.8 Circle shear diagram of magnetorheological fluid
(8)
式中,τy(H)是以磁场强度为自变量的剪切屈服应力函数,具体数值如图4中剪切屈服应力曲线所示;h为磁流变液工作间隙厚度;η为运动黏度,MRF的运动黏度为0.83 Pa·s。
将图7所示径向间隙的磁场强度所对应的剪切屈服应力代入式(8),得出MRF传递的转矩为1.636 N·m。
2.3 联合传动转矩
传动装置的励磁线圈与电热SMA弹簧相连,当传动装置通入电流时,励磁线圈产生的磁场使MRF在毫秒级的时间内产生输出转矩,而电热SMA弹簧输出转矩随温度升高而增大。将MRF传递的转矩MMRF和电热SMA弹簧产生的摩擦转矩Mf相叠加即为装置联合传动产生的转矩:
(9)
由式(9)计算得出的MRF与电热SMA联合传动转矩如图9所示。当施加1 A电流时,磁场强度不变,但电热SMA的温度会逐渐增高。这里需要说明的是,图9中温度是指SMA弹簧的温度。电热SMA热源较为集中,安装位置远离MRF,所以电热SMA弹簧的热量对MRF影响较小。

图9 联合传动转矩Fig.9 Combined drive torque
由图9的计算结果可以看出,单独以MRF传递的最大转矩为1.636 N·m,而通过与电热SMA弹簧联合传动,传动装置所能传递的最大转矩为3.43 N·m,最大转矩增大了1.1倍。
3 试验研究
3.1 电热SMA弹簧压紧力试验
测试热效应下电热加载SMA弹簧力学性能的装置如图10所示,其中TES-1310数显式温度计测量范围为-50.0~200.0 ℃,SH-200N数显式推拉力计的测量范围为0~200.0 N。

图10 压紧力试验装置Fig.10 Compression force test device
SMA弹簧结构参数为:弹簧中径D=8.6 mm,SMA丝的直径d=1 mm,有效匝数n=7,倾角α=6°。电热丝直径d2=0.2 mm,匝数n2=100,并螺旋缠绕在SMA弹簧上。SMA弹簧输出压紧力与温度的关系测试试验是让SMA弹簧一端固定、一端与推拉力计测头端面接触,然后对SMA弹簧通入电流施加电热载荷。
3.2 MRF转矩试验
为测试MRF在圆环状工作间隙的传动性能,搭建的试验装置如图11所示,其中传动性能试验装置连接示意图见图12。试验装置由磁场测量装置、转矩传感器定盘、转动盘、线圈、减速器、电机、电源和调速器组成[18]。

图11 圆环式MRF传动性能试验装置Fig.11 Ring type MRF transmission performance test device

图12 圆环式MRF传动性能试验装置示意图Fig.12 Schematic diagram of ring type MRF transmission performance test device
转动盘底部的轴通过联轴器与减速器相连接,并将MRF填充至定盘的凹槽内,然后将定盘与转动盘相贴合形成密闭的磁流变液工作间隙。装置和传感器安装完成后,启动电机,此时转动盘在电机的驱动下开始旋转,等待电机转速稳定在40 r/min时,改变励磁线圈激励电流的大小。改变励磁线圈电流会改变MRF工作间隙的磁场强度,从而可通过传感器测量出MRF工作间隙的磁场强度与MRF传递的转矩之间的关系。
4 试验结果与讨论
热效应下电热SMA弹簧力学性能测试试验中,每一次的试验对缠绕的电热丝施加的电流始终保持一致;每一次试验安装电热SMA弹簧都与推拉力计测头端面接触但不产生力。经过多次试验,得出电热丝施加的电流为2 A时,电热SMA弹簧的温度与压紧力的关系曲线见图13。

图13 电热SMA弹簧温度与压紧力的关系Fig.13 Relation between electrothermal SMA spring temperature and compression force
由图13可以看出,在电流恒定的情况下,电热SMA弹簧产生的转矩可分为三个阶段。第一阶段,通入电流加热的时间从0~10 s时,电热SMA弹簧温度从60 ℃升高到75 ℃,产生的压紧力缓慢地从0增大到2.1 N;第二阶段,通入电流加热的时间从10~23 s时,电热SMA弹簧温度从75 ℃升高到93 ℃,产生的压紧力快速地从2.1 N增大到18.6 N;第三阶段,通入电流加热的时间从23~35 s时,电热SMA弹簧温度从93 ℃升高到100 ℃,产生的压紧力缓慢地从18.6 N增大到18.75 N;最后,当电热SMA弹簧温度超过100 ℃后,产生的压紧力不再增大。试验测量值与理论计算值基本一致。
在圆环状工作间隙的传动性能测试试验中,驱动电机的转动盘需要稳定到转速为40 r/min时才能开始对线圈进行通电,同样地线圈电流也应当始终保持一致。定盘上的转矩传感器的输出信号稳定后即可记录。通过试验得出励磁线圈的电流为1 A时,MRF与电热SMA联合传动装置传递的转矩如图14所示。当励磁线圈产生不同磁场时,磁场强度与转矩的关系如图15所示。
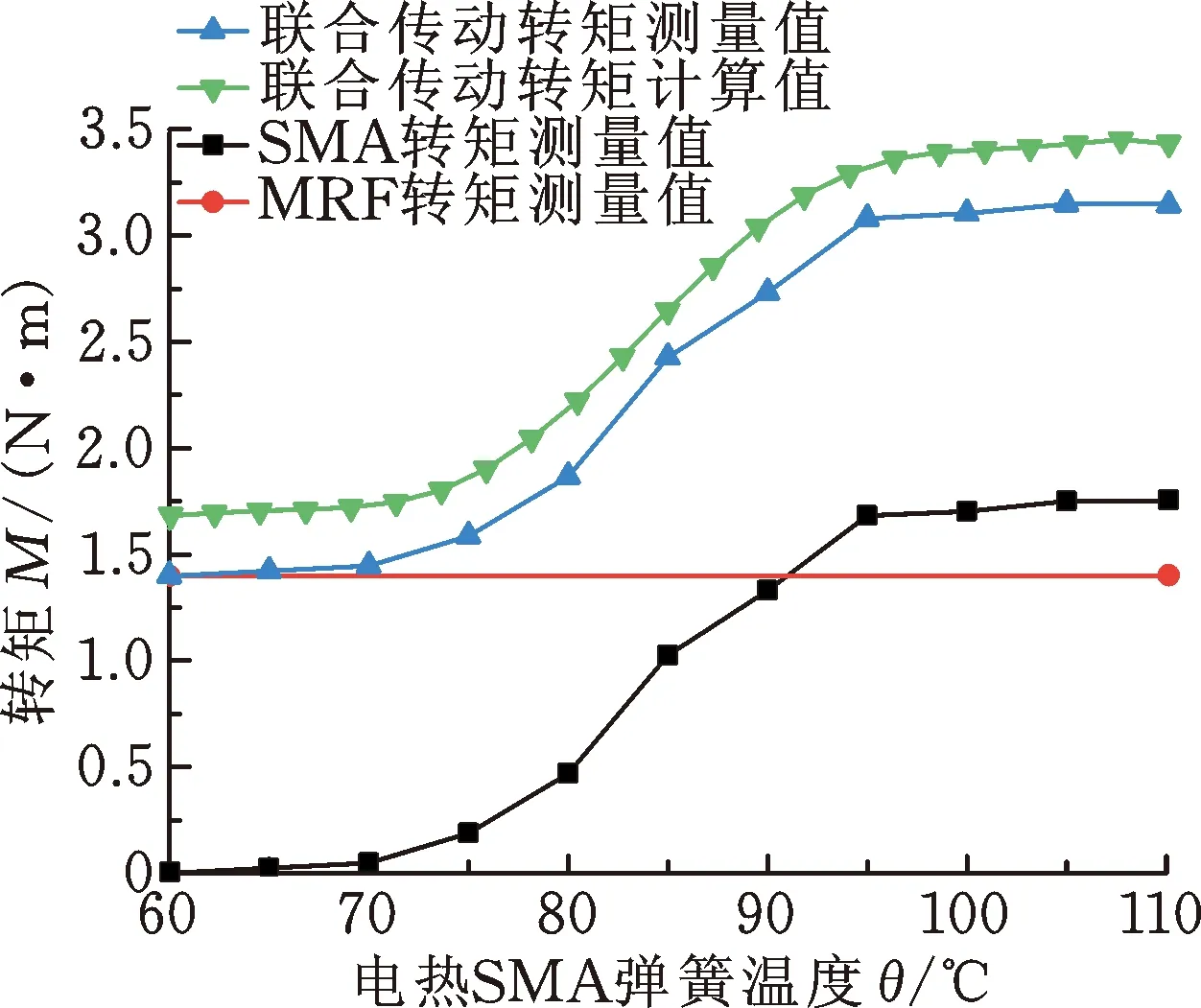
图14 试验测试与理论计算转矩传递比较Fig.14 Comparison of test and theoretical torque
由图14可知,当MRF受到磁场作用时,在极短的时间会产生较大的剪切屈服应力,依靠此应力传递恒定转矩。在试验测量时,MRF传递的转矩为1.41 N·m。联合传动的试验测量转矩为3.15 N·m、理论计算转矩为3.43 N·m,两者相比较,理论计算值偏大0.28 N·m,但试验测量转矩与理论计算转矩增长趋势基本一致。
由图15可知,随着磁场强度增大,MRF产生的转矩趋近于线性增长,其中磁场强度分别为60 kA/m和120 kA/m时,MRF产生的转矩分别为1.2 N·m和2.1 N·m,当电热SMA参与传动时,MRF与电热SMA联合传动转矩分别增大到3.0 N·m和3.8 N·m。通过增大装置磁场强度可以显著增强传动性能。

图15 磁场强度与转矩的关系Fig.15 Magnetic field strength versus torque
上述电热SMA弹簧不同温度下压紧力测试试验中,试验值与理论计算值基本一致;转矩测试试验中,转矩理论计算值与试验测量值存在误差的原因主要来源于MRF材料误差和分析模型的简化。
5 结论
本文提出了一种电热形状记忆合金(SMA)弹簧与磁流变液(MRF)联合传动方法,详细阐述了传动装置的结构与工作原理,计算出了不同温度下电热SMA弹簧的回复力,并推导和计算了多个电热SMA弹簧驱动摩擦盘与主动盘摩擦产生的转矩。通过磁场有限元分析得出了MRF剪切应力,然后推导和计算了圆环状MRF工作间隙产生的转矩,最终得出联合传动转矩的公式。
相关试验表明,电热SMA弹簧的温度为60 ℃时开始产生回复力,温度上升到100 ℃时弹簧的回复力达到最大值18.75 N,由8个电热SMA弹簧产生的摩擦转矩最大值为1.798 N·m,与理论计算值相比偏小3.7%。励磁线圈的电流为1 A、匝数为380时,MRF工作间隙的磁场强度最大值为311.60 kA/m,MRF传递的转矩为1.41 N·m,与理论计算值相比偏小5.2%。相较于单一的MRF传动装置产生的转矩最大值为1.41 N·m,MRF与电热SMA联合传动产生的转矩为3.15 N·m,传动性能提升了1.2倍。

