基于液滴分析的高温高压流体喷射闪蒸模型研究

蔡本安，李石磊，郭民承，王海军

(1.东北电力大学 能源与动力工程学院，吉林 吉林 132012；2.中广核研究院有限公司，广东 深圳 518031；3.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049)

在核电站实际运行过程中，由于管道热疲劳及热分层[1-3]等问题的存在，可能会导致管道泄漏的出现。在核电站一回路系统中，流经反应堆堆芯的冷却剂压力可达15.5 MPa，温度可达327 ℃，即为高温高压状态，此时一旦在管道某个位置发生泄漏，高温高压的流体经过压力突降，达到过热状态并迅速发生蒸发，此为闪蒸现象。闪蒸具有分离效果好、蒸发强度大、冷却能力高等优点，因此广泛应用于海水淡化[4]、航空飞行器部件冷却[5-6]等领域。另外，在核电站管道系统中，利用冷却剂泄漏闪蒸产生大量水蒸气的特点，可以布置相应的设备来监测管道泄漏的出现，从而保证核电站安全可靠地运行。

闪蒸作为一种特殊的蒸发形式与常规蒸发不同。在常规蒸发过程中，液体蒸发所需的能量主要来自外界环境对液体的加热，而在闪蒸过程中，液体蒸发所需的能量主要来自液体本身的过热度，液体的显热转化为汽化潜热。已有研究针对闪蒸过程提出了相应的闪蒸模型。Shin等[7]采用扩散控制的蒸发模型计算喷射闪蒸过程中液滴温度的瞬态变化，认为蒸汽产生速率与液滴表面和环境中的浓度差有关，由于液滴直径约为100 μm，所以他们忽略了液滴的自然对流，通过实验值及模型计算值的对比可看到，模型计算值高于同工况下的实验值。Duan等[8-9]采用无网格移动粒子法(MPS)对高温高压喷射闪蒸中的射流长度进行了研究，计算发现射流长度随过热度增加而减少，并随射流温度逐渐接近喷射压力下的饱和温度，射流长度对过热度的依赖程度逐渐降低。Wu等[10-11]基于扩散模型计算了低温低压条件下的液滴闪蒸，研究发现减小液滴直径，液滴温度在短时间更加迅速地下降，液滴闪蒸速率受相对湿度的影响很大。Cheng等[12]采用有效导热系数模型对真空喷射闪蒸进行了研究，研究发现有效导热系数模型比Shin等[7]的模型精度有所提高。Chen等[13]给出了闪蒸室中液滴闪蒸的数学模型，研究发现初始液滴流速的减小增强了能量利用效率，而过热度的增加对能量利用效率的变化几乎无影响。随后，Chen等[14]根据模型计算值及实验数据的对比，反推了液滴尺寸的变化，研究发现液滴直径比喷嘴直径小几个数量级，过热度和流速增大导致液滴尺寸的减小。Ji等[15]基于过热液滴闪蒸所需能量由内部过热能量提供这一理论基础，建立了过热液滴闪蒸数学模型，其中闪蒸蒸发速率采用Adachi等[16]提出的实验关联式进行计算，将模型计算结果与实验数据对比发现该模型的相对误差可达到35%。

目前国内外学者针对喷射闪蒸的模型研究主要集中在低温低压喷射闪蒸方面，他们的模型多数基于扩散模型发展而来，该模型在低温低压情况下比较适用，但在高温高压领域不再适用。由于高温高压工质喷射闪蒸实验难以操作，获得微观传热传质方面信息的难度非常大。值得注意的是，本文提到的低温低压喷射闪蒸，指的是喷射压力低于0.2 MPa、温度低于333.15 K条件下的喷射闪蒸，而高温高压喷射闪蒸，指的是喷射压力大于6 MPa、温度高于423.15 K条件下的喷射闪蒸。为了对高温高压流体喷射闪蒸的热力学特性进行理论研究，有必要建立高温高压条件下过热液滴喷射闪蒸的模型，加深对高温高压喷射闪蒸的理解。

1 模型建立

为简化计算，突出闪蒸的基本特点，建立喷射闪蒸模型时做了以下假设：1) 假设液滴为球形，液滴物性为各向同性；2) 忽略液滴之间的相互作用；3) 忽略液滴的旋转运动，即计算液滴受力时默认液滴的角速度为0。

1.1 液滴运动计算

对于液滴向下运动时，液滴的受力分析如图1所示。其中，重力Fg、浮力Fb和曳力Fd分别为：

图1 液滴受力分析图Fig.1 Schematic of droplet force analysis

Fg=mg

(1)

Fb=ρvgV

(2)

(3)

式中：m为液滴质量，kg；g为重力加速度，m·s-2；ρv为水蒸气密度，kg·m-3；V为液滴体积，m3；A为液滴截面积，m2；CD为曳力系数；ud为液滴速度，m·s-1。

液滴速度可由下式计算得到：

(4)

式中，t为时间，s。

液滴的运动距离s可由下式计算得到：

(5)

1.2 液滴传质计算

现有计算低温低压流体喷射闪蒸的模型主要以Spalding蒸发理论为基础，该理论定义了传质系数Bd如下：

(6)

式中：Ys为液滴表面的水蒸气质量分数；Y∞为大气环境中的水蒸气质量分数。

在高温高压流体喷射闪蒸过程中，过热度非常大，在液滴表面附近发生剧烈闪蒸，导致大量水蒸气产生，液滴表面的Ys趋近于1，导致Bd趋近无穷大，这意味着液滴将在瞬间蒸发，显然是不合常理的，因此已有的计算低温低压流体喷射闪蒸的模型不适用于本文计算。对于过热度很大的情况，连续射流的存在时间很短，由于气泡的形成、长大，射流破碎变成很多小液滴。对于高过热度条件下的闪蒸，该过程由液滴内部的可用过热能量所控制。蒸发速率采用Adachi等[16]提出的实验关联式进行计算：

(7)

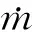
Adachi等通过实验研究与理论分析相结合的方法，研究了液体燃料正戊烷(C5H12)的喷射闪蒸过程，基于实验结果分析得到了过热液滴闪蒸的总体传热系数的表达式为：

(8)

由于式(8)中得到的传热系数是针对C5H12实验得到的，且该传热系数是绝对过热度的函数，这个过热度的值不是无量纲的值，对于其他液体，如水，水的物性与C5H12的物性明显不同，该传热系数的通用性值得商榷[17]。

为了计算得到水喷射闪蒸过程中液滴闪蒸的传热系数，需将式(8)中过热度进行无量纲化处理。将C5H12与水进行比较分析，由于C5H12闪蒸发生在相对较低的温度水平，在过热度ΔT相同的情况下，导致C5H12的实际过热效果大于水，即同样的过热度导致的实际传热系数并不相同，式(8)中液滴过热度与饱和温度有关，因此采用C5H12的饱和温度进行标准化和无量纲化。喷射流体为水时，式(8)中过热度的计算公式为：

(9)

式中：ΔTC5H12为喷射液体为C5H12时式(8)中对应的过热度，K；ΔTH2O为喷射液体为水时式(8)中对应的过热度，K；Tsat,C5H12为C5H12的饱和温度，K；Tsat,H2O为水的饱和温度，K。

喷射工质为水时得到的传热系数αsh,H2O为：

(10)

考虑到液滴内部的质量传递，有必要增加一个修正系数φ[11]。对于液滴直径小于1 μm的情况，φ=0.91；对于液滴直径小于0.1 μm的情况，φ=0.42。该修正系数φ的值可通过分析相应的实验结果得到。φ的计算公式[18]为：

(11)

式中：λ为扩散平均自由行程，m；r为液滴半径，m。

最终得到液滴半径的变化关系式为：

(12)

式中，ρd为液滴密度，kg·m-3。

1.3 液滴传热计算

为提高本文喷射闪蒸模型的精度，将导热、对流及辐射换热均考虑在内。基于能量守恒，液滴的温度变化为：

(13)

式中：cpd为液滴比热容，J·kg-1·K-1；D为液滴直径，m；ε为发射率；σ0为黑体辐射常数，W·m-2·K-4；T∞为周围环境温度，K；keff为有效导热系数。

有效导热系数由下式[19]计算得到：

keff=1.86k+0.86ktanh(2.245lg(Ped/30))

(14)

式中：k为导热系数，W·m-1·K-1；Ped为液滴佩克莱数。

2 计算方法与验证

本文模型通过MATLAB编程实现，模型中的一阶隐式微分方程通过龙格-库塔算法实现。由于本研究中流体温度变化范围较广，Kneer等[20]的研究结果表明，液滴的物性对液滴直径和温度的变化有一定影响。因此，在本文模型计算过程中将液滴物性随液滴温度的变化考虑在内，从而提高了该模型的计算精度。

本文主要研究高温高压流体喷射闪蒸的热力学特性，选取液滴无量纲温度θ及闪蒸效率η作为主要研究内容。

(15)

式中：Tz为距离喷嘴出口z处的射流温度，K；T0为初始流体温度，K。

闪蒸效率η指闪蒸蒸发量与给水流量的比值，即：

(16)

(17)

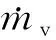
为了表征喷射闪蒸强度，本文对喷射闪蒸速率SFS进行了计算分析。SFS指的是单位时间内过热能量的消耗速率：

(18)

为了对本文提出的模型进行验证，分别计算了相应的液滴无量纲温度及闪蒸效率，并与实验值进行对比。无量纲温度间的对比如图2所示，实验值为Miyara等[21]的实验数据，其中初始流体温度为303.15 K，过热度为7 K，流速为1.8 m/s，液滴初始直径的计算详见文献[22]。表1列出闪蒸效率实验值和计算值对比，实验数据来自文献[23]。表1中：ηexp为闪蒸效率的实验值；ηcal为闪蒸效率的计算值；pev为闪蒸压力。

图2 无量纲温度的实验值与计算值对比Fig.2 Comparison between experiment and calculation values of dimensionless temperature

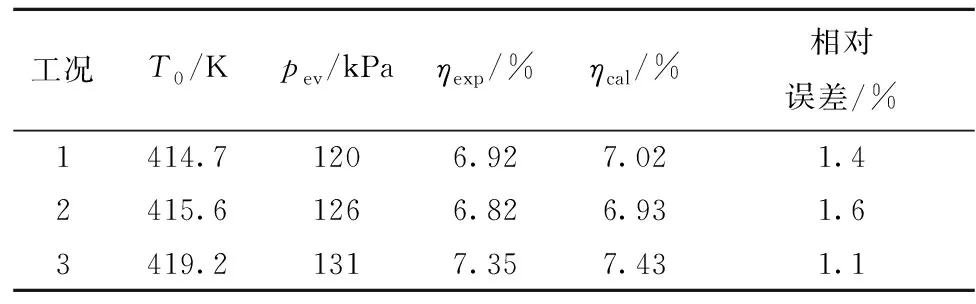
表1 闪蒸效率实验值与计算值对比Table 1 Comparison between experiment and calculation values of flashing efficiency

由图2和表1可看出，无论是液滴无量纲温度还是闪蒸效率，计算值与实验值均吻合良好，表明本文模型研究结果是可靠的，可用来描述高温高压工质喷射闪蒸过程。

3 计算结果与分析

3.1 液滴温度分布

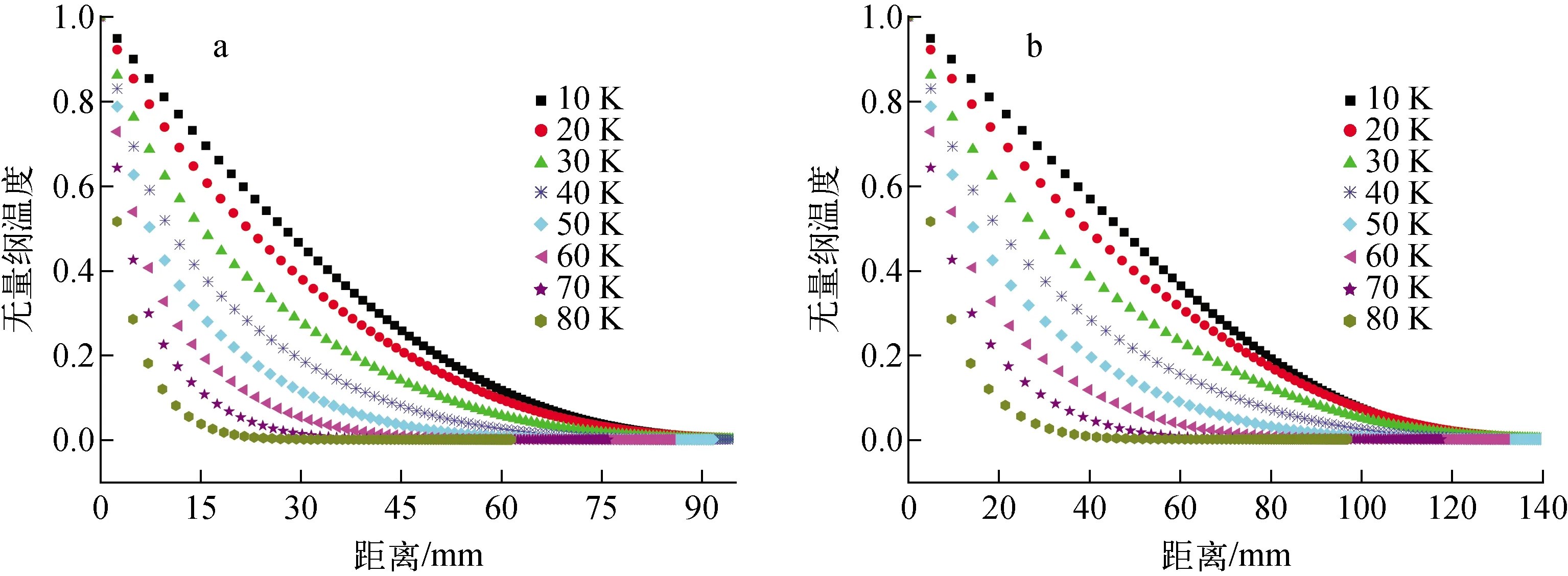
根据液滴温度的计算公式可知，液滴尺寸对液滴温度的瞬态变化有非常重要的作用，而通过实验方法评估液滴尺寸对高温高压喷射闪蒸的影响存在较大难度。因此，本文采用模型计算的方法分析液滴尺寸的作用规律。图3示出液滴无量纲温度随喷射距离的变化，其中液滴直径变化范围为40～180 μm，初始流体温度为463.15 K，过热度为20 K，喷射压力为8 MPa。在下面计算中喷射压力保持8 MPa不变。由图3可见，随液滴运动距离的增大，液滴无量纲温度逐渐降低。按照无量纲温度定义，最初为最大值1，随着闪蒸进行，液滴温度逐渐降低，直至达到平衡温度为止，之后液滴无量纲温度保持为0不再发生变化。在液滴直径为60 μm及液滴流速u为20 m/s的情况下，达到平衡状态所需的运动距离为32 mm，这与Ramcke等[17]的研究相符。在Mutair等[24]的低温低压喷射闪蒸研究中，达到平衡状态所需的距离为400 mm左右，这主要是因为在高温高压状态下射流破碎形成的液滴尺寸非常小，液滴比表面积显著增大，相应的换热能力增强，从而导致液滴温度下降的速率明显提高。图3计算结果表明，在液滴未达到平衡状态前，随液滴尺寸的增大，相同距离处的液滴无量纲温度随之增大，这充分反映了液滴尺寸对喷射闪蒸的显著影响。对比图3a、b可知，流速增大导致液滴达到平衡状态所需的距离相应增加，由此导致液滴尺寸对液滴温度分布的影响范围相应拓宽。

液滴流速：a——20 m/s；b——60 m/s图3 液滴尺寸对液滴温度分布的影响Fig.3 Influence of droplet size on droplet temperature distribution

为了开展模型对比分析，将Ji等[15]的过热液滴闪蒸模型与本文模型进行对比分析，如图4所示。Ji等的蒸发速率采用了Adachi提出的实验关联式，未进行修正，且在传热计算中没有充分考虑导热、对流及辐射换热的影响。由图4可看到采用Ji等的模型计算得到的无量纲温度偏大，在液滴尺寸为80 μm的条件下，对应相同的距离s=25 mm处，本文模型计算得到的无量纲温度为0.176，Ji等的模型为0.595。

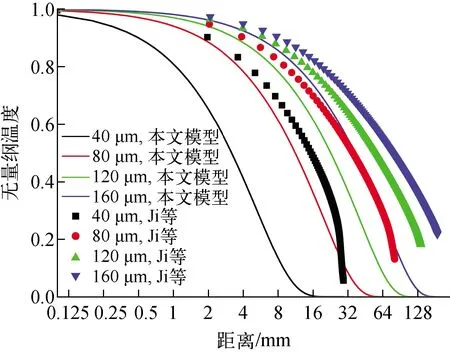
T0=463.15 K，u=20 m/s，ΔT=20 K图4 液滴温度分布计算对比Fig.4 Comparison of calculated droplet temperature distribution

由液滴闪蒸计算公式可知，除液滴尺寸外，液滴过热度同样对流体闪蒸具有重要影响。无论是总传热系数还是蒸发速率均与液滴过热度直接相关，因此本文对过热度的影响机制开展研究。图5示出不同过热度条件下液滴温度的空间分布，其中初始流体温度及液滴流速保持不变。过热度的增大导致液滴闪蒸达到平衡状态所需的距离明显缩短，这是因为过热度增大意味着有更多的非平衡能量供运用，更多的能量驱动闪蒸进行，导致在更短的距离内由非平衡达到了平衡状态。即使在高温高压状态下，过热度对喷射闪蒸热特性的影响仍不可忽略。另外在相同位置处，过热度大的液滴无量纲温度反而较小，这充分体现了过热度对高参数液滴闪蒸的驱动作用。将图5a、b比较分析可知，流速增大导致液滴达到平衡状态所需的距离相应增加，由此导致过热度对液滴温度分布的影响范围相应拓宽。

液滴流速是喷射闪蒸过程的一个重要因素。根据闪蒸模型的计算公式可知，液滴的运动与液滴流速的变化直接相关。目前液滴流速对高温高压喷射闪蒸热特性的影响机制尚不明确，相关研究较为稀少，因此本文开展了相应研究。图6示出不同过热度下流速由20 m/s增大至90 m/s过程中的液滴空间温度分布。在流速较大的情况下，同一位置处的液滴无量纲温度较大，液滴闪蒸达到平衡状态所需的距离更大。图7示出不同流速条件下液滴温度随时间的变化，可看到液滴闪蒸达到平衡状态所需的时间与流速无关。这是因为液滴运动速度主要影响液滴的运动距离，液滴完成闪蒸所需的时间未受到流速的影响。随流速的增大，液滴在相同闪蒸室内的停留时间减少，液滴用来蒸发的时间减少，由图7可知，液滴蒸发时间减少则对应的液滴无量纲温度增加。在管内流体泄漏过程中，液滴流速代表了泄漏率，说明在泄漏率增加的情形下，液滴温度达到平衡状态所需要的距离也增加。另外，相比液滴尺寸及过热度的影响效果，流速对高温高压喷射闪蒸热特性的影响程度更小，这主要是因为在高温高压状态下，液滴尺寸较小，液滴完成闪蒸所需的时间非常短(毫秒级)，流速的影响相对而言就降低了。

a——T0=463.15 K，u=20 m/s；b——T0=463.15 K，u=40 m/s图5 过热度对液滴温度分布的影响Fig.5 Influence of superheat on droplet temperature distribution

a——T0=463.15 K，ΔT=40 K；b——T0=463.15 K，ΔT=20 K图6 流速对液滴温度分布的影响Fig.6 Influence of flow velocity on droplet temperature distribution

a——T0=463.15 K，ΔT=40 K；b——T0=463.15 K，ΔT=20 K图7 不同流速条件下液滴温度随时间的变化Fig.7 Variation of droplet temperature with time at different flow velocities

3.2 闪蒸效率

图8～10示出闪蒸效率的变化。在一定尺寸的闪蒸室内，此时对应的液滴运动距离是固定值，流速的增大导致闪蒸效率呈现下降的趋势。如图8所示，在s=40 mm处，闪蒸效率由0.075 1降低为0.043 3。理论上而言，在其他参数不变的情况下，流速的增大会导致闪蒸量的增加[13]。至于闪蒸效率下降则是因为给水流量也随流速增大而显著增加，且给水流量的增加效果更加显著。在本文设定的高温高压条件下，在s=140 mm处，流速变化对闪蒸效率的影响已经非常微弱。如图9所示，过热度对闪蒸效率的影响趋势与流速的相反，在喷射距离20～140 mm范围内，过热度增加导致闪蒸效率明显上升，并且闪蒸效率与过热度近似呈现线性关系。在s=80 mm处，过热度由20 K增大至90 K，闪蒸效率由0.017 8增大为0.158。研究结果表明，在广泛的液滴运动距离范围内，过热度作为闪蒸的驱动力，增加过热度总能保证闪蒸效率的有效提高。如图10所示，相比过热度及流速对闪蒸效率的影响，液滴尺寸变化对闪蒸效率的影响程度相对较小。液滴直径增加，导致换热能力降低，在其他参数不变的条件下，闪蒸效率随之降低。在喷射距离s=40 mm处，液滴直径由40 μm增大至180 μm，相应的闪蒸效率由0.043 1减小为0.009 3。结合液滴温度分布可知，液滴尺寸减小导致同一位置处的液滴无量纲温度降低及完成闪蒸所需的距离显著减少，而降低液滴尺寸对闪蒸效率的提升效果有限。

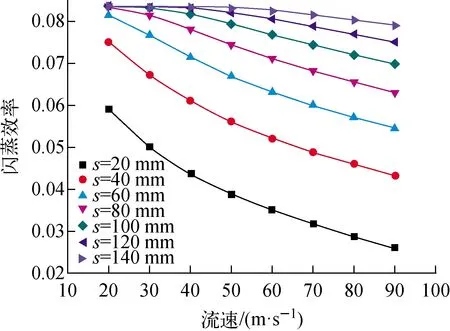
T0=463.15 K，ΔT=40 K图8 闪蒸效率随流速的变化Fig.8 Variation of flashing efficiency with flow velocity

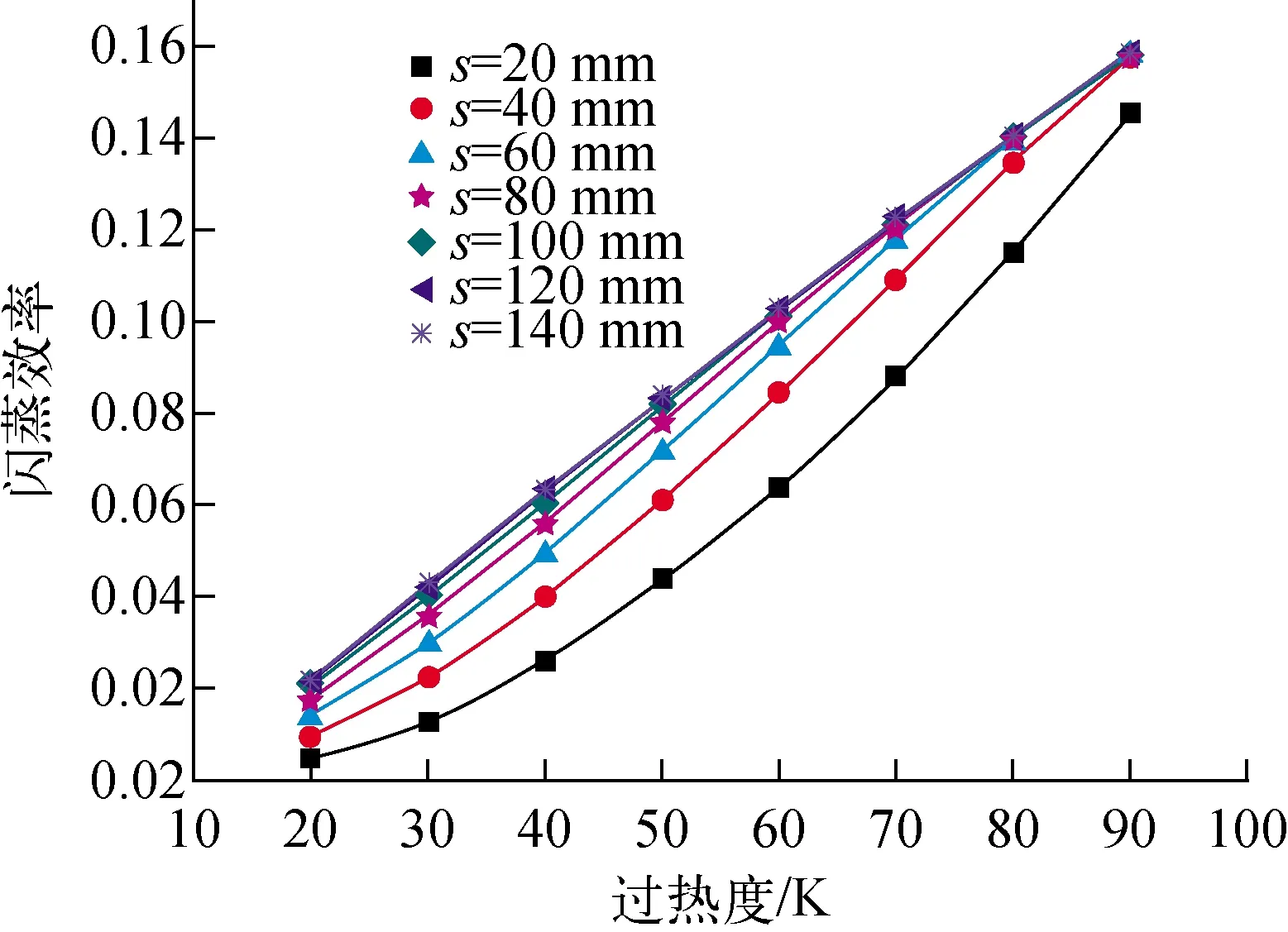
T0=463.15 K，u=40 m/s图9 闪蒸效率随过热度的变化Fig.9 Variation of flashing efficiency with superheat

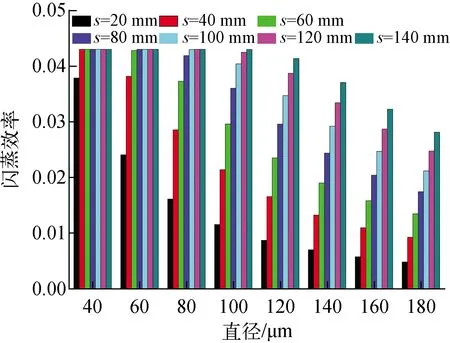
T0=463.15 K，u=60 m/s，ΔT=20 K图10 闪蒸效率随液滴尺寸的变化Fig.10 Variation of flashing efficiency with droplet size

图11示出闪蒸效率的模型计算对比，可看到Ji等的模型计算得到的闪蒸效率偏小，由液滴无量纲温度分布的对比可知，采用Ji等的模型计算得到的无量纲温度偏大，而闪蒸效率与液滴温度有关，由式(16)和(17)可知，偏大的液滴温度对应偏小的闪蒸效率。

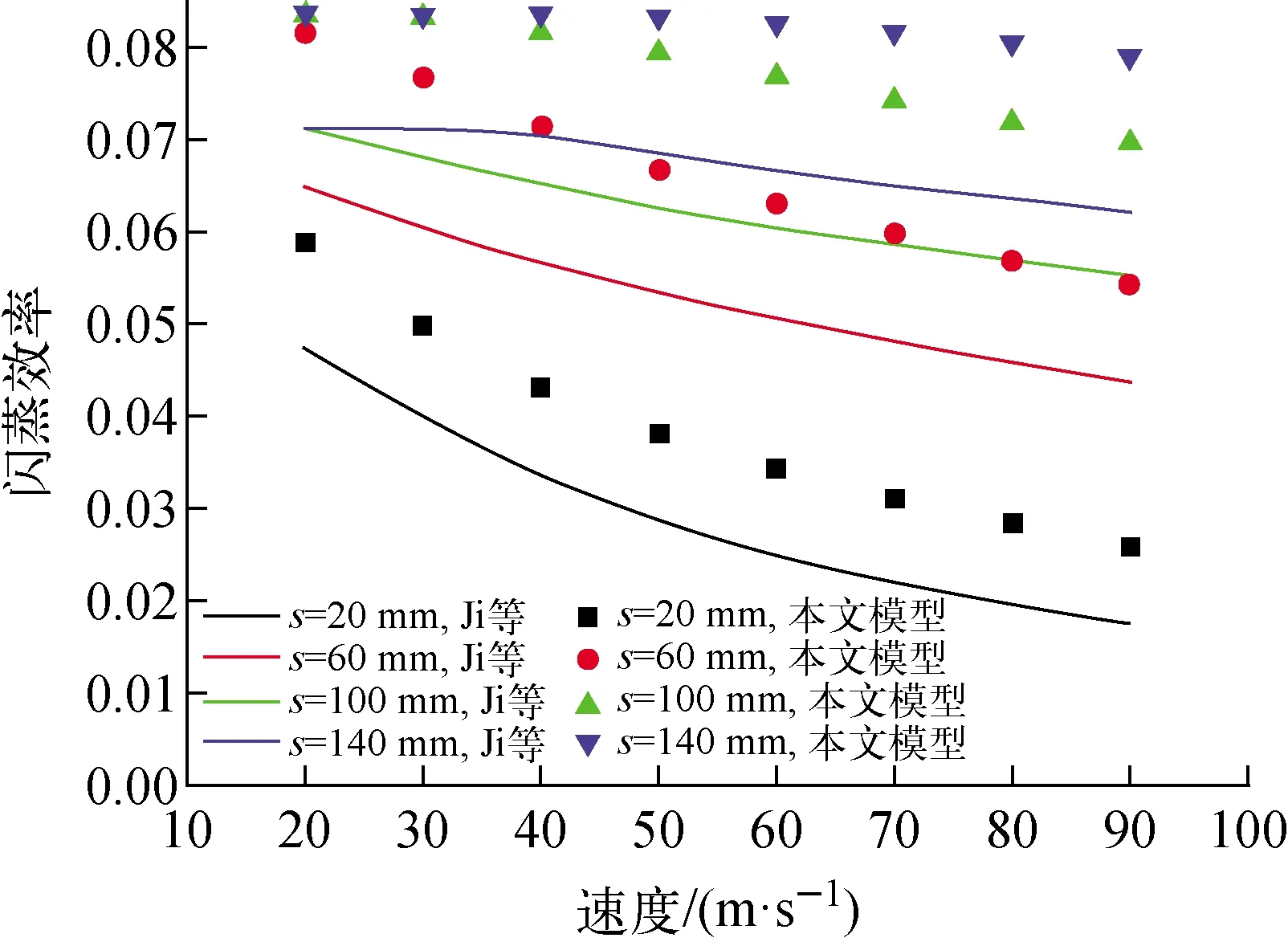
T0=463.15 K，ΔT=40 K图11 闪蒸效率计算对比Fig.11 Comparison of calculated flashing efficiency

3.3 闪蒸强度

图12示出不同流速条件下SFS的变化。由图12可知，在泄漏口附近SFS最大，随液滴运动距离增加，SFS急剧下降。以图12a中流速为40 m/s为例分析，在液滴运动距离为2 mm处，SFS为1 404.8 s-1，到s=144.5 mm处，SFS为77 s-1。根据SFS的定义可知，其数值大小表征了闪蒸强度。由前述可知，液滴运动距离增加意味着闪蒸时间增加，即随着闪蒸的进行，喷射闪蒸强度在很短距离内剧烈下降。根据已有研究可知，静态闪蒸及循环闪蒸速率小于1 s-1[25]，低温低压喷射闪蒸速率小于40 s-1[22]，而根据图12a可知，SFS最大值可达1 465 s-1。因此，与静态闪蒸、循环闪蒸、低温低压喷射闪蒸相比，高参数流体喷射闪蒸强度更大，充分说明流体初参数的提高导致喷射闪蒸强度显著增强，核电站一回路管道泄漏导致的流体闪蒸是一个非常剧烈的相变过程。由图12可看到，在同一位置处，随液滴流速的增加，SFS相应增加，说明液滴流速的增大导致相同位置处喷射闪蒸强度相应提高，这主要是由液滴停留时间降低导致的。这表明在泄漏速率较大的情形下，流体喷射闪蒸强度也非常大。

a——T0=463.15 K，ΔT=40 K；b——T0=463.15 K，ΔT=20 K图12 流速对SFS的影响Fig.12 Influence of flow velocity on spray flash speed

图13示出SFS的模型计算对比，可看到采用Ji等的模型计算得到的SFS偏小，由液滴无量纲温度分布的对比可知，采用Ji等的模型计算得到的无量纲温度偏大，单位时间内液滴温度的变化偏小，由式(18)可知，采用Ji等的模型会得到偏小的SFS。

T0=463.15 K，ΔT=40 K图13 SFS计算对比Fig.13 Comparison of calculated spray flash speed

图14示出不同液滴尺寸下SFS随距离的变化。液滴尺寸对闪蒸强度的影响在不同距离处并不相同。在较小距离范围内，液滴尺寸的减小导致闪蒸强度显著增大，随着液滴运动距离增加，较小的液滴尺寸导致了较小的闪蒸强度。这是因为在较小距离内，液滴闪蒸处于发展阶段，较小的液滴尺寸将促进换热，从而导致单位时间内的液滴温度迅速下降，在这种情况下SFS得到提高。达到一定距离后，较小的液滴逐渐发展到充分的闪蒸阶段，此时液滴温度变化很小，对应的SFS反而较小。这反映了液滴尺寸对闪蒸强度的影响有个转折点，将转折点对应的液滴运动距离称为转折距离。由图14可知，流速的增加导致液滴尺寸对闪蒸强度影响的转折距离增大，以液滴直径120 μm与180 μm为例，流速为20 m/s时，转折距离为73.3 mm，即在s<73.3 mm和s>73.3 mm区间，液滴尺寸分别对闪蒸强度起到了相反的影响效果，而流速为60 m/s时，转折距离为127 mm。

a——T0=463.15 K，u=20 m/s，ΔT=20 K；b——T0=463.15 K，u=60 m/s，ΔT=20 K图14 液滴尺寸对SFS的影响Fig.14 Influence of droplet size on spray flash speed

图15示出过热度对闪蒸强度的影响。与液滴尺寸的影响程度类似，过热度对闪蒸强度的影响也有个转折点。以图15a中过热度80 K及20 K为例，在s<69.8 mm处，过热度为80 K对应的SFS明显大于过热度为20 K对应的SFS，过热度作为闪蒸的驱动力，提高过热度对闪蒸强度起到了增强的效果。在s>69.8 mm处，过热度为80 K对应的SFS小于过热度为20 K对应的SFS，这是因为过热度大的液滴在更短的距离内达到平衡，此时相同位置处过热度大的液滴更接近平衡状态，单位时间内的液滴温度变化较小，从而导致SFS较小。根据图15a、b比较可知，流速的增加同样导致转折距离变大。

a——T0=463.15 K，u=40 m/s；b——T0=463.15 K，u=20 m/s图15 过热度对SFS的影响Fig.15 Influence of superheat on spray flash speed

4 结论

针对高温高压条件下的喷射闪蒸热力学特性，本文基于液滴分析建立了相应的数学模型，并采用模型计算分析了液滴温度分布、闪蒸效率及闪蒸强度，具体的结论如下。

1) 本文建立的模型综合考虑了液滴运动、液滴传热、液滴传质及液滴物性随温度的变化，并与实验结果进行了对比验证，研究发现该模型计算精度较高，可有效描述高温高压流体喷射闪蒸热力学特性。

2) 减小液滴尺寸会导致同一位置处的液滴无量纲温度明显降低，提高过热度可有效降低液滴闪蒸达到平衡状态所需的距离，流速变化对液滴喷射闪蒸热力学特性的影响主要体现在液滴温度的空间分布，对液滴温度的时间分布几乎无影响。

3) 流速变化导致给水流量及闪蒸量同时变化，最终产生的效果为流速增大导致一定空间内的闪蒸效率降低。过热度作为闪蒸驱动力，增加过热度在大范围内能保证闪蒸效率的提高，相比液滴尺寸变化对无量纲温度分布的影响，改变液滴尺寸对闪蒸效率的影响程度相对较小。

4) 流体初参数的提高导致闪蒸强度显著增强，液滴流速增大导致同一位置处闪蒸强度相应提高。液滴尺寸及过热度对喷射闪蒸强度的影响有个转折点，在转折点前后影响效果相反，流速的增加导致转折距离随之增大。

由于本文模型做了几个假设，这些假设可能会导致对实际问题的预测存在一些偏差。如假设液滴形状为球形，液滴物性为各向同性。事实上，液滴形状对液滴的运动、液滴的传热传质会产生复杂的影响，因此，基于球形液滴计算得到的结果与实际不规则形状情况下的闪蒸热力学特性会有所不同，在后续研究中可考虑液滴形状变化对流体喷射闪蒸特性的影响。本模型忽略了液滴的旋转运动，这样计算得到的液滴运动轨迹为直线，而实际情况下液滴运动轨迹非常复杂，并不一定是规则的路线，这也需要进一步研究。本模型忽略了液滴之间的相互作用，这对计算也有一定的影响。液滴间的相互作用对液滴分布、液滴形状、液滴尺寸等具有非常复杂的影响，如两液滴碰撞聚合变成一个液滴，液滴尺寸即会增大，根据原较小尺寸计算得到的无量纲温度则会偏小，因此液滴间相互作用对喷射闪蒸特性的影响也需要进一步探索。