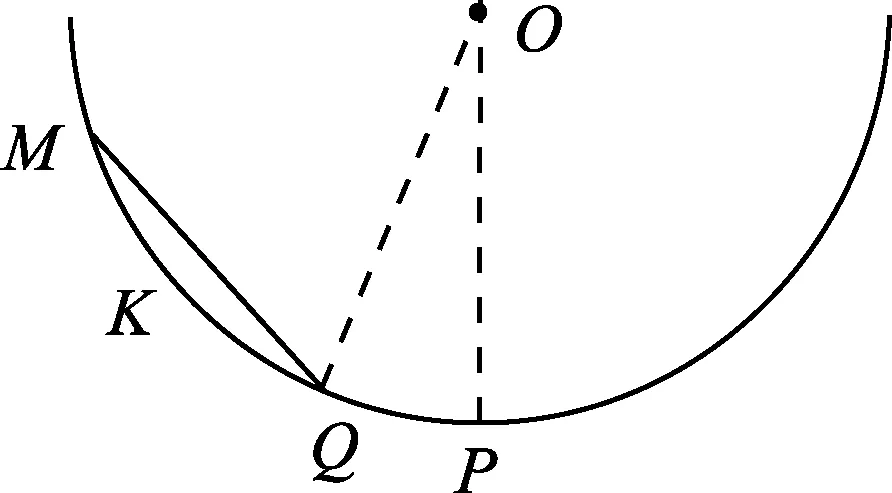
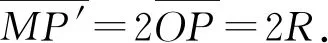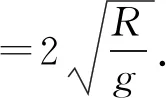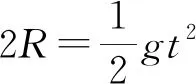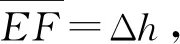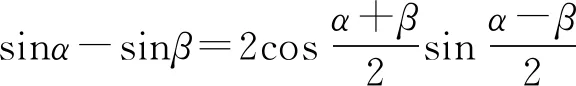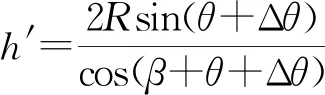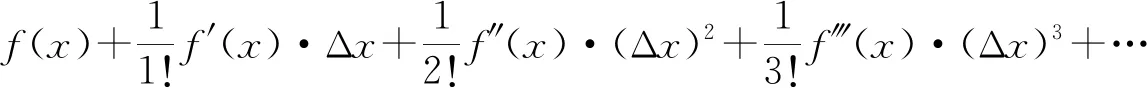谁先滑至弧底?
王孝厂 王金聚
(浙江省温州中学,浙江 温州 325000)
物体在沿着光滑的圆弧轨道下滑时,其加速度的大小和方向都是在不停地变化的,故其下滑的具体时间,除了一些特殊的情况外,在中学阶段一般很难求出.但确有一些关乎圆弧轨道下滑的题目,不是要求我们求出它的下滑时间,而是去比较它沿圆弧与沿直线轨道下滑的快慢,这对大多数学生甚至老师而言,还是有不小难度的.
1 物体在小角度圆弧轨道上运动的时间问题
小球在光滑的圆弧轨道上运动时,分析一下它的受力情况,可发现与单摆小球的受力情况极为相似,是故它们的运动规律也十分雷同.所以,小球在光滑圆弧轨道上运动的时间,在圆弧最低点一侧的轨迹所对的圆心角不超过5°的情况下,我们可以用单摆的周期公式来进行计算和比较.这种考查方式在高考试卷中也不时会有所体现.
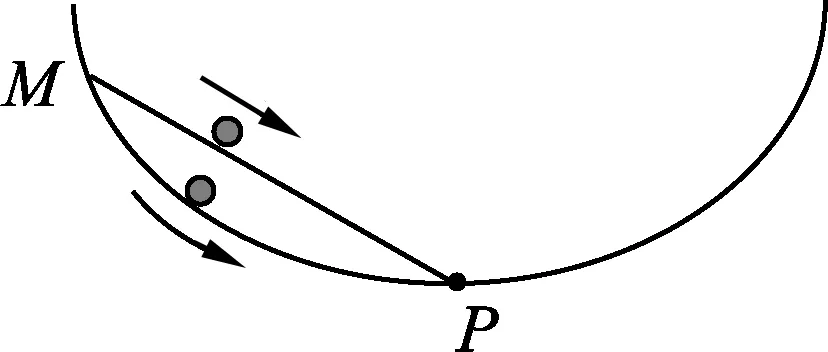
如图1所示,在竖直平面内有一段光滑的圆弧轨道MN,它所对的圆心角小于10°,P是圆弧的最低点,也是圆弧MN的中点.在N、P之间搭一光滑斜面,将两个相同的小球分别从M点和N点同时由静止释放,谁先到达P点呢?
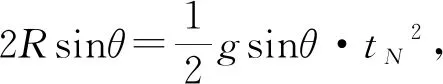
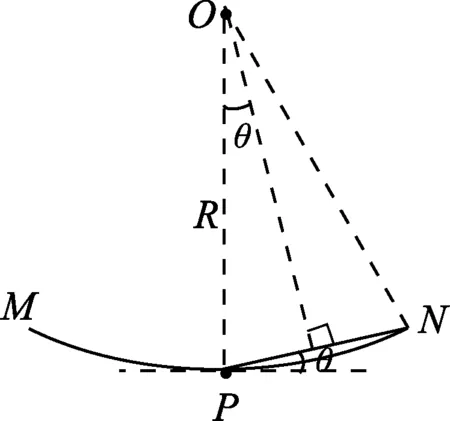
图2
(1)
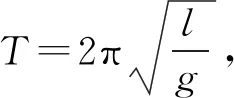
(2)
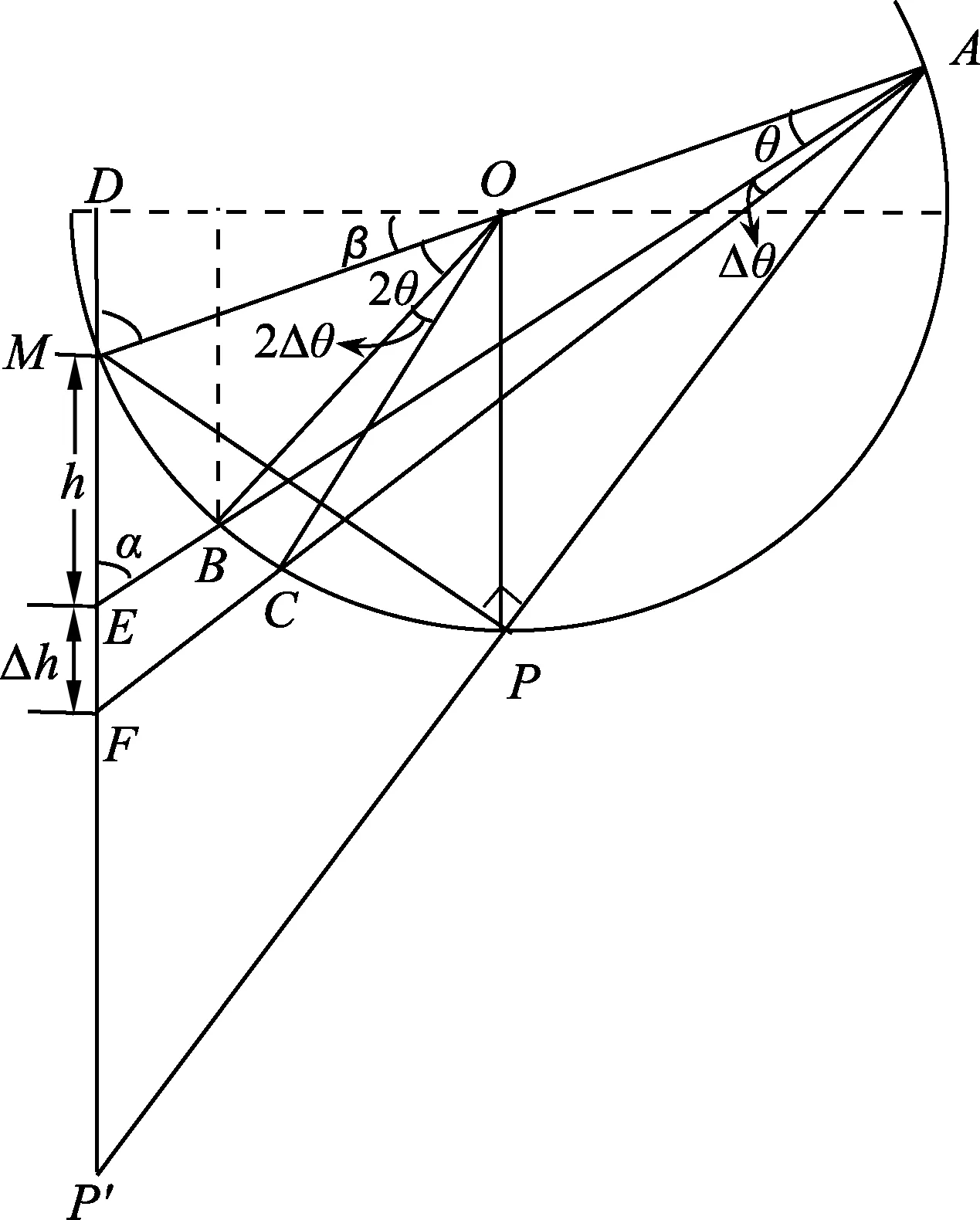
比较(1)、(2)式可知tM 能得出这一结论的前提是左侧圆弧所对的圆心角不超过5°,若圆弧所对的圆心角较大,单摆的周期公式不再适用时,小球沿圆弧轨道和直线轨道下滑的快慢如何比较?这一问题,在教学中往往会被学生问及,也确是令大多教师都觉得很难论证回答的问题. 如图3所示,在竖直平面内有一光滑的圆弧轨道,P为圆弧的最低点,M为圆弧上的任意一点,沿MP修一光滑的弦轨道,当两个小球分别沿弦轨道和圆弧轨道上的M点同时释放时,谁先到达P点呢? 图3 因为M为圆弧上的任意一点,而单摆的周期公式在这里不具有普适性,所以我们需另寻其他途径来予以论证. 图4 由(1)式可知,小球沿弦轨道MP下滑的时间为 (3) (4) 比较(3)、(4)式可知t弦=t,所以我们只需比较小球沿圆弧MP轨道下滑与小球自由下落MP′段所用的时间长短即可. 圆弧MB所对的圆心角为2θ,小圆弧BC所对的圆心角为2Δθ,小圆弧的弧长lBC=2RΔθ.设直线OM与水平方向的夹角为β,则M、B两点的竖直高差为 hMB=Rsin(2θ+β)-Rsinβ. (5) 可得小球经过小圆弧BC段的时间为 (6) 在△AME中,外角∠AMD=90°-β=α+θ,所以α=90°-(β+θ).设M、E点的高度差为h,在△AME中,由正弦定理得 所以E、F两点的高度差为 (7) 下面我们对该式进行化简. 因Δθ是极小量,应用泰勒公式 对函数cos(β+θ+Δθ)进行泰勒展开并取一阶小量,得 cos(β+θ+Δθ)≈cos(β+θ)- sin(β+θ)·Δθ. (8) 对函数sin(θ+Δθ)进行泰勒展开并取一阶小量,得 sin(θ+Δθ)≈sinθ+cosθ·Δθ. (9) 将(8)、(9)式代入(7)式得 小球自由落体到E点的速度为 所以,小球下落经Δh段的时间为 (10) 比较(6)、(10)两式可得 (11) 要保证滑块能沿圆弧无初速下滑,轨道最高点不应高于圆心.即图中角度关系满足0°≤β<90°,β≤β+θ<90°,即β、β+θ均为锐角,所以cos(β+θ) 考虑角度θ、β取值的任意性,所以对小球走过的任一小段圆弧而言,与其对应的自由落体运动那段相比较,其用时关系都有t小弧 因为M点取位的任意性,所以我们就可以得到一般式t弧 实际上,弦轨道的下端也不一定非得是在圆弧轨道的最低点,如图5所示.对弦轨道MQ和圆弧轨道MKQ而言,从以上的证明过程也显而易见,关系式t弧 图5 简单地讲,沿圆弧轨道下滑的物体之所以最先达到末端,原因就在于物体在刚开始下滑时,其加速度较之于对应的弦轨道要大一些,故它在初始阶段的速度增加得较快,虽然它沿圆弧运动的路程比弦轨道是远了些,但这并不足以改变它最先到达轨道终点的最终结果了.2 物体沿任意角度的圆弧轨道与弦轨道下滑的快慢比较