局部减薄圆柱壳爆破压力试验研究与计算方法
陈虹港,李思源,马建生,李祚成,苗世得,张玉福,苏嘉庆
(1.机械工业上海蓝亚石化设备检测所有限公司,上海 201518;2.兰州石油机械研究所有限公司,甘肃 兰州 730050;3.中国石油 大连石化公司,辽宁 大连 116011)
在压力容器和管道中,由于介质腐蚀、冲蚀和机械损伤等原因,其器壁和管壁可能产生局部减薄缺陷,影响构件的安全性能和完整性。为了评估局部减薄构件在内压工况下的完整性,国内外开展了大量的试验研究,取得了很多成果,制定发布的评定标准有美国的 ASME B31G—2009《Manual for Determining the Remaining Strength of Corroded Pipelines》[1]、API 579-1/ASME FFS-1—2007 《Fit-for-Service》[2]、 英国 BG 和挪威DNV合作发布的 DNV RP-F101—2004《Corroded Pipelines》[3]以及我国的GB/T 19624—2004《在用含缺陷压力容器安全评定》[4]等。国外的研究以局部减薄圆柱壳的内压爆破试验为基础,采用试件爆破压力试验数据和有限元计算数据进行拟合,得到计算构件爆破 (失效)压力的经验公式。在评定计算公式中,对圆柱壳局部减薄缺陷尺寸,一般只使用沿壁厚的减薄深度和沿轴向减薄长度,而没有考虑缺陷沿环向的宽度对失效压力的影响[5-7]。我国对局部减薄圆柱壳的强度研究主要利用有限元和数值分析方法求解构件的内压极限载荷,然后进行拟合,得出剩余强度系数的拟合计算公式[8-10]。文献[11-12]利用有限元方法研究局部减薄缺陷沿壳体环向宽度对内压极限载荷的影响,得出的结果是,评定局部减薄圆柱壳剩余强度时,不能忽略局部减薄宽度的影响。但用试验结果验证还比较少。为此设计制作了一批局部减薄圆柱壳试件,在内压试验中测定试件的爆破压力和爆破载荷剩余强度系数试验值RSFbt。对RSFbt进行拟合,提出了规则化减薄圆柱壳爆破载荷剩余强度系数RSFb的计算式,应用RSFb计算式提出了一种计算规则化减薄直管道爆破压力pb的计算式,其计算结果和文献[13-15]中的试验结果符合。
1 局部减薄圆柱壳试件爆破试验
1.1 试件设计
设计无缺陷圆柱壳试件,圆柱壳的外直径2Ro=112 mm,壳壁厚度t=10 mm,壳体长度L=450 mm。设计的局部减薄缺陷圆柱壳试件见图1。图1中,a为减薄深度,2xo为沿壳体轴向减薄长度,2θ为沿壳体环向减薄夹角。
1.2 试件制作
以φ114 mm×12 mm钢管为原材料,分4步制作圆柱壳试件。①将φ114 mm×12 mm钢管加工成2Ro=112 mm、t=10 mm的圆柱壳。②在2Ro=112 mm、t=10 mm的圆柱壳上加工整圈均匀减薄缺陷。③在2Ro=112 mm、t=10 mm的圆柱壳上截取长度为2xo的圆柱壳,用电火花在其外壁(或内壁)上切割深度为a、周长度为 2xo、环向夹角为2θ的规则化减薄。④采用气体保护焊焊接各对接焊缝及平封头。
总共制作了10件20钢和22件Q345B圆柱壳试件,各试件几何尺寸见表1和表2。

表1 20钢制含规则化减薄圆柱壳试件几何尺寸及其剩余强度系数试验数据

表2 Q345钢制含规则化减薄圆柱壳试件几何尺寸及其剩余强度系数试验数据
20钢圆柱壳试件中,试件10为无缺陷圆柱壳试件,其余均为外壁减薄圆柱壳试件。Q345R圆柱壳试件中,试件11和试件12为无缺陷圆柱壳试件,试件17~试件22为内壁减薄圆柱壳试件,其余为外壁减薄圆柱壳试件。
1.3 材料力学性能
圆柱壳试件材料20钢管的平均实测屈服强度σs=280.9 MPa,平均实测抗拉强度σb=468.0 MPa;Q345的平均实测抗拉强度σs=366.5 MPa,平均实测抗拉强度σb=494.4 MPa。
1.4 内压爆破试验
在圆柱壳试件的外壁选定测试点,在测试点粘贴电阻应变片,对试件进行内压试验。用电测法测定各测点的应变和压力-应变曲线,直至有测点屈服,而且当应变超过 5 000μ ε时,停止应变测量,并对试件连续缓慢升压,直至试件爆破,确定试件试验的塑性最大压力pmaxt和爆破压力pbt,结果见表1和表2。
2 圆柱壳试件爆破载荷剩余强度系数计算
2.1 剩余强度系数定义
局部减薄圆柱壳的剩余强度系数RSFf定义为局部减薄圆柱壳失效压力pf与无缺陷圆柱壳失效压力pof的比值,即RSFf=pf/pof。不同的失效压力定义又将RSFf区分为,①屈服载荷剩余强度系数RSFL。当局部减薄圆柱壳和无缺陷圆柱壳的失效压力都取屈服强度极限载荷,其值分别为pL和poL时,RSFL=pL/poL。②塑性最大载荷剩余强度系数RSFmax。当局部减薄圆柱壳和无缺陷圆柱壳的失效压力都取塑性最大载荷,其值分别为pmax和pomax时,RSFmax=pmax/pomax。③爆破载荷剩余强度系数RSFb。当局部减薄圆柱壳和无缺陷圆柱壳的失效压力都取爆破压力,其值分别为pb和pob时,RSFb=pb/pob。
2.2 无缺陷圆柱壳试件失效压力计算
已知材料失效应力σf和圆柱壳结构尺寸(图1),可用式(1)计算圆柱壳试件的失效压力pf:

将表1中试件10的几何尺寸Ro、t和爆破压力 pob=82.5 MPa代入式(1),计算得 20钢制无缺陷圆柱壳试件的材料爆破应力σf=360.99 MPa。再将σf=360.99 MPa代入式(1)并进行化简得到式(2)。

采用类似的方法进行推导,可得到式(3)。同样地,结合式(1)和表 2中试件11和试件 12的压力试验数据,推导出式(4)和式(5)。

对于表1中所有圆柱壳试件,应用式(2)计算出其对应的无缺陷时的爆破压力pob,应用式(3)计算出其对应的无缺陷时的塑性最大压力pomax,结果见表 1。
对于表2中所有圆柱壳试件,应用式 (4)计算出其对应的无缺陷时的爆破压力pob,应用式(5)计算出其对应的无缺陷时的塑性最大压力pomax,结果见表 2。
2.3 局部减薄圆柱壳试件剩余强度系数试验值计算
在已知圆柱壳试件塑性最大载荷试验值pmaxt、爆破载荷试验值pbt、塑性最大载荷计算值pomax、爆破载荷计算值pob的情况下,可用式(6)和式(7)计算圆柱壳试件的塑性最大载荷剩余强度系数试验值RSFmt和爆破载荷剩余强度系数试验值RSFbt。

对表1和表2中所有圆柱壳试件,应用式(6)和式(7)计算 RSFmt和 RSFbt,具体计算结果见表1和表2。
2.4 圆柱壳试件压力试验数据和计算数据分析
对表1和表2中的数据进行综合分析,得出的规律和推论如下。
(1)表1和表2中所有局部减薄圆柱壳试件的塑性最大载荷试验值pmaxt都大于或等于它的爆破压力试验值pbt。
(2)表 1中的试件用 20钢制作,表 2中的试件用Q345制作。当表1和表2中局部减薄试件的尺寸、凹坑尺寸相近时,两者相应的剩余强度系数试验值RSFmt和RSFbt都分别相近。由此得出,局部减薄圆柱壳试件的剩余强度系数与试件材料无关,而只与局部减薄结构尺寸有关。
(3)在表 2 中,试件 2、试件 4、试件 5(外壁减薄试件)和试件17、试件18、试件19(内壁减薄试件)的几何尺寸、缺陷尺寸分别相近,内壁减薄试件的剩余强度系数RSFmt和RSFbt都分别高于相应的外壁减薄试件数据。
(4)从表2内壁减薄圆柱壳试件18、试件20、试件21和试件22数据可以看出,当规则化减薄区的长度2xo相同,减薄深度a也相同时,试件的剩余强度系数试验值RSFmt和RSFbt都随着减薄区环向夹角2θ的增大而减小,而且环向夹角的变化对RSFmt和RSFbt的影响都很明显。
(5)从表 1和表2可以看出,规则化减薄圆柱壳试件的爆破载荷剩余强度系数试验值RSFbt都大于它的塑性最大载荷剩余强度系数试验值RSFmt,但它们满足不等式:

(6)以塑性最大载荷为失效压力时,圆柱壳试件的剩余强度系数RSFmt均不大于1;而以爆破载荷为失效压力时,剩余强度系数RSFbt出现了大于1的情况。由此推断,对局部减薄圆柱壳试件,采用塑性最大载荷剩余强度系数比采用爆破载荷剩余强度系数更合理。但是考虑到,①现有文献中已给出的一般都是圆柱壳试件的爆破压力,而没有塑性最大载荷。②在理论计算分析中,一般都是将圆柱壳试件的理论计算值和爆破压力比较。因此,仍推荐采用爆破载荷定义局部减薄圆柱壳试件的剩余强度系数。在下面的理论计算和分析中,一律采用爆破载荷剩余强度系数RSFb。
3 规则化减薄圆柱壳构件爆破载荷剩余强度系数计算
对图1所示圆柱壳几何尺寸及缺陷尺寸参数,令:

式中,R=Ro-t/2, 为圆柱壳的中半径;α、γ、b 为规则化参数,且α≤0.8,γ>0,b≤1。式(9)为圆柱壳上局部减薄缺陷的规则化。当b=1时,圆柱壳为整圈均匀减薄。
3.1 整圈均匀减薄圆柱壳剩余强度系数拟合计算式
文献[16-17]对外壁整圈均匀减薄圆柱壳试件开展了爆破压力试验研究,将得到的试件爆破压力和爆破载荷剩余强度系数数据拟合成整圈均匀减薄圆柱壳构件剩余强度系数RSFl计算式:

本研究项目补充了一批规则化减薄圆柱壳试件的试验,得到了试件的爆破载荷剩余强度系数试验值 (表1和表2的RSFbt),并用它们对式(10)进行局部修正,得到式(11):

3.2 规则化减薄圆柱壳剩余强度系数计算
将规则化减薄参量α和γ代入式(11),计算整圈均匀减薄圆柱壳剩余强度系数RSFl。令:

经计算分析后发现,规则化减薄圆柱壳的爆破载荷剩余强度系数RSFb可采用式(13)进行拟合:

φ(g)是以g为参数的权函数。利用表1和表2中的试验值RSFbt进行分段拟合,确定φ(g)并代入式(13)得到式(14),用于外壁规则化减薄圆柱壳爆破载荷剩余强度系数RSFb的计算。在式(14)中,α、γ、b 由式(9)确定,RSFl用式(11)计算,g 用式(12)计算。

3.3 拟合计算式验证
3.3.1 外壁规则化局部减薄圆柱壳
对式(14)的计算精度和可靠性进行检验。应用式(14)计算表1、表2以及文献[9]中外壁规则化减薄圆柱壳试件的爆破载荷剩余强度系数RSFb,并将计算结果和试件的爆破载荷剩余强度系数 RSFbt列于表3。

表3 规则化减薄圆柱壳试件爆破压力剩余强度系数计算值和试验值比较
表3中,误差η=(RSFbt-RSFb)/RSFbt×100%。从表3可以看出,计算值RSFb和试验值RSFbt的误差在-2.49%~4.36%,误差绝对值平均为1.87%,其中计算值小于试验值的试件数量占比超过2/3。因此用式(14)计算外壁规则化减薄圆柱壳爆破载荷剩余强度系数RSFb具有满意的计算精度和可靠性。
3.3.2 内壁规则化局部减薄圆柱壳
采用式(14)计算表2中内壁规则化减薄圆柱壳试件的爆破载荷剩余强度系数RSFb,结果见表 4。
从表4可以看出,试件的RSFb都小于对应的 RSFbt,计算误差 η在 2.25%~11.10%。据此判断,采用式(14)计算的内壁规则化减薄圆柱壳的爆破载荷剩余强度系数RSFb是安全的。

表4 内壁规则化减薄圆柱壳试件爆破压力剩余强度系数计算值和试验值比较
4 局部减薄圆柱壳爆破压力计算
已知无缺陷圆柱壳的爆破压力pob,又采用式(14)计算规则化减薄圆柱壳的爆破载荷剩余强度系数RSFb,则可按式(15)计算局部减薄圆柱壳的爆破压力pb:

获得无缺陷圆柱壳爆破压力pob的方法有:①直接法。用材料、几何尺寸和规则化减薄圆柱壳都相同的无缺陷圆柱壳进行爆破试验,确定其爆破压力pob。②估算法。用经验公式计算无缺陷圆柱壳的爆破压力pob。估算法常用的经验公式有Faupel公式(略)和平均直径公式:

DNN RP-F101—2004中用式(16)计算无缺陷管道的失效压力pof。该标准适用于中高强度钢管道的失效压力评估。对于中高强度钢管道,将式(16)代入式(15)得到规则化减薄直管道爆破压力pb计算式:
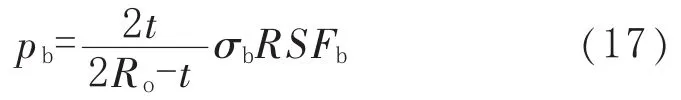
式中的RSFb用式(14)计算。
文献[14-15]列出了管道用钢X60和X65含缺陷试件在内压下的爆破压力pbt,将试件的尺寸参数、pbt以及用式(17)计算的各试件爆破压力pb列于表5。
表5中,序号1~序号9试件的材料为X60,其抗拉强度σb=589.6 MPa;序号10~序号16试件的材料为X65,其抗拉强度σb=556.6 MPa。外壁规则化减薄圆柱壳的参数b=w/(2πRo),w为环向减薄宽度。误差η'=(pbt-pb)/pbt×100%。
从表 5可以看出,pb和 pbt误差在-4.1%~5.2%,误差绝对值平均为2.21%,其中计算值小于试验值的试件数量比例为75%。据此认为,用式(17)计算管道钢X60和X65规则化减薄直管道的爆破压力具有满意的精度。又由于式(17)是用式(14)计算试件的RSFb值,因此表 5的结果也表明采用式 (14)计算规则化减薄圆柱壳的爆破载荷剩余强度系数RSFb是可行的。
表3~表5中47个试件的误差数值表明,用式 (14)计算规则化减薄圆柱壳的爆破载荷剩余强度系数RSFb具有满意的计算精度和可靠性。因此认为,式(14)全面地反映了圆柱壳规则化减薄的几何参数对爆破载荷剩余强度的影响。

表5 规则化减薄管道钢试件爆破压力计算值和试验值比较
5 结语
(1)制作了一批钢制规则减薄圆柱壳试件,测定了其内压试验爆破压力。分析试验爆破压力后认为,圆柱壳规则减薄参数α、2xo和2θ对试件的爆破压力都有不可忽略的影响。应用试件爆破压力测定数据计算了爆破载荷剩余强度系数。
(2)由试件的爆破压力数据得到了试件的爆破载荷剩余强度系数RSFbt。用规则化减薄参数α、γ、b和RSFbt等数据进行拟合,建立了规则化减薄圆柱壳爆破载荷剩余强度系数RSFb的计算式(14),其计算值和试验值RSFbt符合。因此计算式 (14)能准确地反映规则化减薄参数α、γ和b对爆破载荷剩余强度系数的影响。
(3)应用 RSFb计算式(14)提出了规则化减薄圆柱壳爆破压力pb的计算式(17)。对中高强度钢管道,16个试件的计算值和试件爆破压力pbt的误差在-4.1%~5.2%。

