综合考虑水平和竖向地震作用的边坡稳定数方法

阎飞，靳宝

（北京京能地质工程有限公司，北京 102300）

0 引言

稳定性分析是边坡工程设计中一项十分重要的工作。目前，按照稳定性计算是否需要进行数值算法求解，边坡稳定分析方法可以分为解析法和数值法两大类。其中，极限平衡法即为解析法的代表，边坡规范中的不平衡推力法即为极限平衡法的一种。数值法主要包括有限元法、边界元法、光滑粒子法等。

不排水前提下，有限均质边坡稳定安全系数的确定通常需要采用泰勒稳定图（Taylor,1937,1948）。根据工况以及假设条件的不同，国内外学者提出并论证了多种边坡稳定性分析技术方法（Janbu,1954;Bishop,1955;Price and Morgenstern,1965;Spencer,1967;Majumdar,1971;Sarma,1973;Ling et al.,1997;Ling and Leshchinsky,1998;Chowdhury et al.,2009;Cheng and Lau,2014;Duncan et al.,2014）。

一般而言，当作用载荷为静载荷时，能够借助泰勒稳定图轻松实现对稳定数的求解。然而地震作用所带来的影响却未能体现在传统泰勒稳定图中。由于强度较大的破坏性地震往往会导致边坡失稳，因此若能将地震作用带来的影响在传统泰勒稳定图中加以体现，就能为边坡工程抗震设计带来极大便利。在泰勒稳定图法完善过程中，国外学者引进土体修正摩擦角指标时考虑了水平地震影响（Majumdar,1971）。水平地震影响通常是边坡稳定图分析需要考虑的一个主要因素，但尽管如此，地震力垂直分量同样应引起高度关注，这已被最新研究成果证实（Chopra,1966;Lew,1991;Ling et al.,1999;Shukha and Baker,2008），其之所以如此，主要是由于动应力分布会在竖向地震影响下而发生显著改变（Lew,1991）。纵观美国旧金山大地震（Stewart and Ashford,1994）、北岭地震（Bardet et al.,1995）以及阪神大地震（Aoi et al.,2008）等世界范围内曾发生过的大型地震可以发现，竖向地震作用所带来的影响不容忽略，在某些案例中最大竖向地震作用甚至不小于水平地震作用。例如，阪神大地震的垂直加速度就是水平加速度的130%（Aoi et al.,2008），而岩手-宮城内陆地震的水平加速度仅为垂直加速度的50%（Dawson et al.,1999）。为了更好地分析地震作用下边坡的稳定性及位移变化，Ling et al.（1999）借助对数螺旋法对相关问题进行了研究，研究结果显示：当地震过程中同时存在水平及垂直加速度时，边坡稳定性会发生较为显著的变化。

本文以前人（Majumdar,1971）工作为基础，同时将水平和竖向地震作用考虑在内，改进传统泰勒稳定图，以期对地震多发区的边坡稳定性研究提供参考。

1 改进稳定数法

1.1 相关公式推导

根据传统泰勒稳定图，当土体内摩擦角φ保持不变时，稳定数c/（F·γ·H）和边坡倾角i是一一对应的。其中，c、F、γ和H分别表示土体粘聚力、边坡安全系数、土体重度和边坡高度。原始泰勒边坡稳定图所对应的公式在推导过程中做了假设前提：（1）待研究的边坡土质是均匀的；（2）不同深度处土体粘聚力c保持恒定；（3）以总应力法加以分析；（4）破坏面为圆形且通过边坡坡脚；（5）破坏面土体抗剪强度适用摩尔-库仑准则。

在继续坚持上述假设的基础上，Majumdar（1971）考虑水平地震作用，提出了修正的摩擦角的概念，将传统的边坡稳定图拓展到了水平地震作用情况。本文同时考虑水平和竖向地震作用，在此工作的基础上做进一步的分析。

图1所示为某一高度为H，边坡倾角为i的均质黏土坡断面，圆柱面FE为该边坡的潜在破坏面，且该圆柱面半径为R，圆心为O(h,k) 。破坏弦线EF与水平面之间夹角为α0，破坏圆中心角为20β，由以上两个角度可确定圆心O(h,k) 位置。

图1 土坡几何图

滑动体FGE受力情况：（1）重力W，作用点为重心处；（2）水平地震作用力Fh，以及竖向地震作用力Fv，作用点均为重心处。Fh方向一般取远离边坡的水平方向，Fv方向一般取竖直向上（下）；（3）粘聚力C，方向沿破坏面；（4）摩擦抗力，方向沿破坏面切向。

于是滑动体的体积力WE可表示为：

（1）式中，V为潜在滑动土体的体积，γE为综合考虑W、Fh以及Fv后的等效重度，又

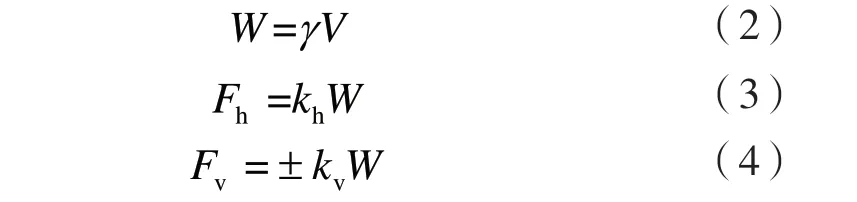
上述（2）、（3）、（4）各式中，W为滑动土体自重，kh和kv分别为水平地震系数和竖向地震系数。

将体积力WE对圆心O 求矩，力矩可表示为

（5）式中，d和l分别表示竖向、水平地震作用的力臂。综合上述5式并作必要简化，即可得

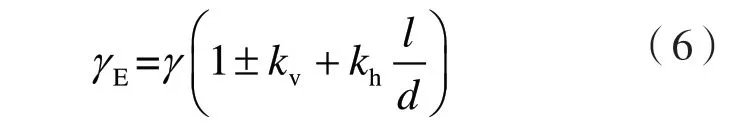
如图1，对单位厚度且重量为Wj的第j片竖向土条，其宽度取Δx，y1和y2分别表示土条底部和顶部距水平轴的实际距离。不考虑粘聚力引起的抗力作用，则总抗力可表示为

式（7b）中，θj为第j片竖向土条底部中心切线和水平线之间所形成的夹角，b为滑动体在水平面形成的投影长度

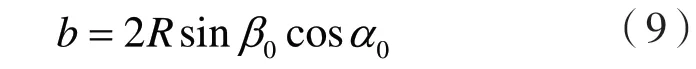
式（9）中，β0表示滑动弧所对应圆心角的一半，α0表示滑动弧顶点连线和水平线之间的夹角。

除粘聚力引起的抗力作用外的总抗力可表示为

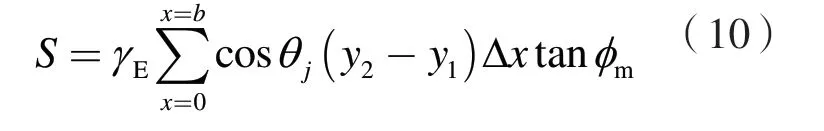
式（10）中，φm为抗震修正后的内摩擦角。由式（7b）及式（10）可以得到

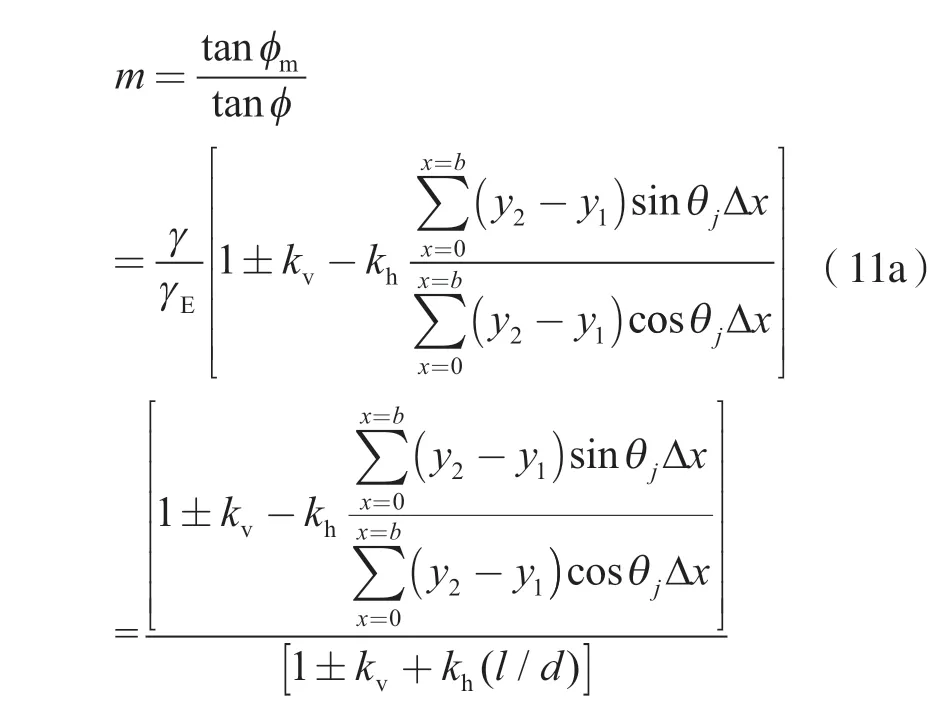
式（11a）中，m表示将水平和竖向地震作用内摩擦角考虑在内后的折减系数。特别的，如果此时忽略竖向地震作用，也即kv=0，则简化为Majumdar（1971）的研究结果；如果水平和竖向地震作用都不加以考虑，即kv=kh=0，则简化为Taylor（1937）的研究结果。令

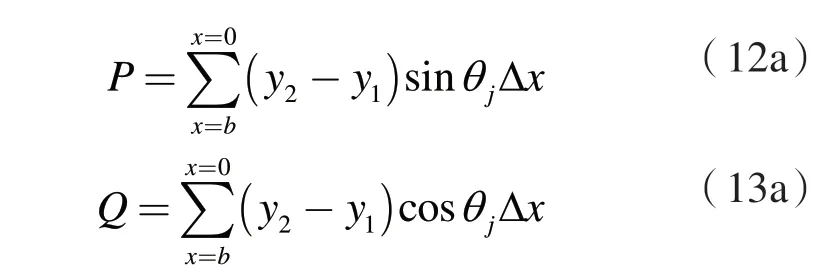
则，式（11a）可简写为

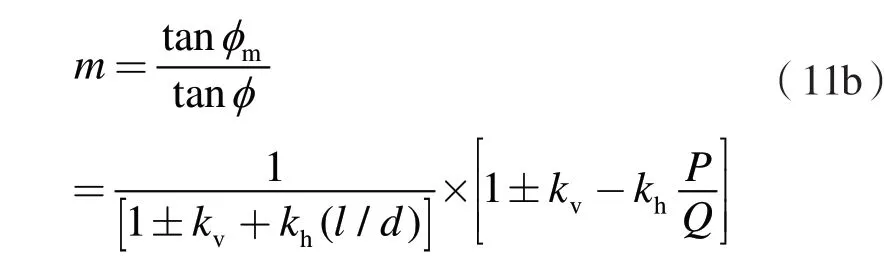
当Δx→0 时，根据数学积分有

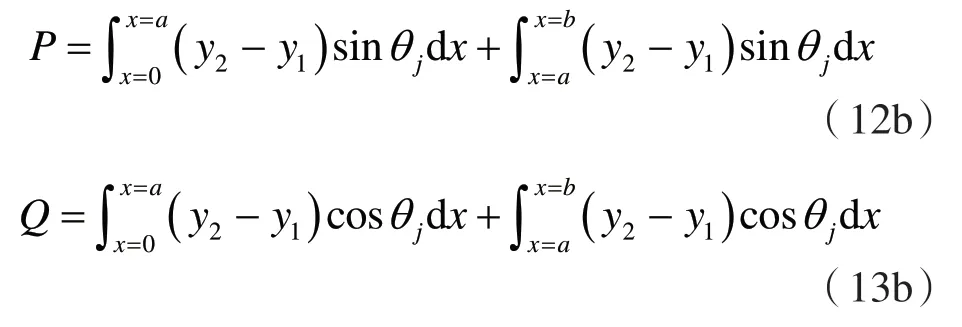
其中，a表示坡顶边缘到坡脚距离的水平投影长度，具体为

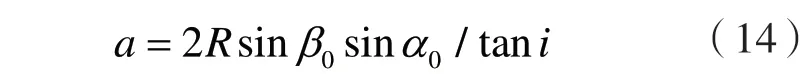
根据如图1所示的几何关系，易得

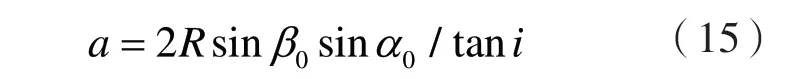
潜在破坏面对应的圆心为O(h,k)，则如图1所示的x-y坐标下满足

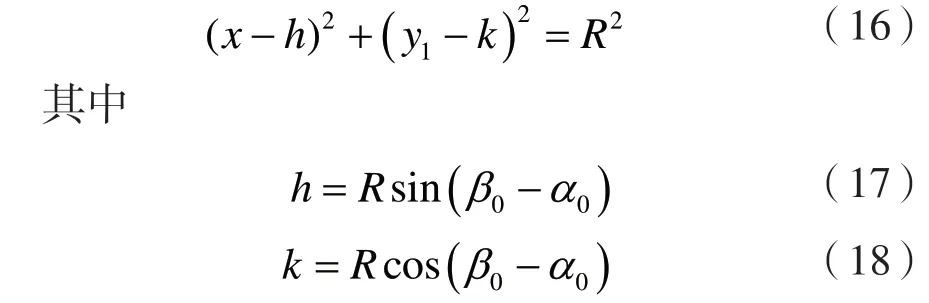
对式（16）微分后易得

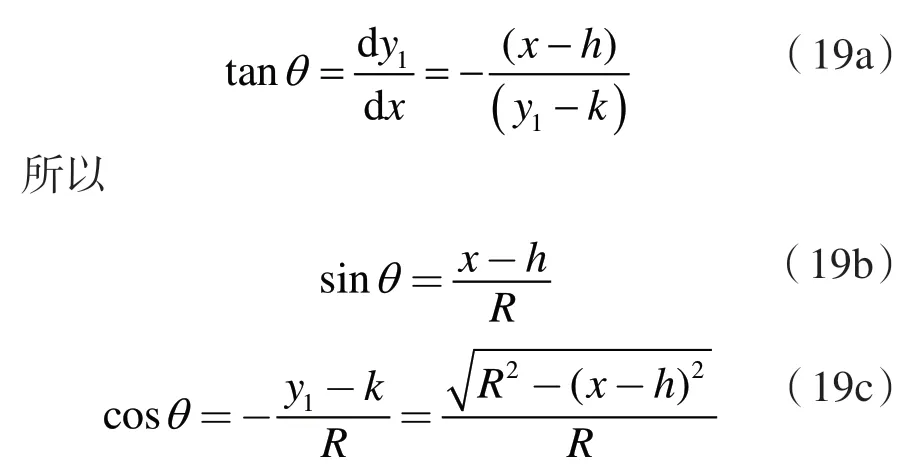
综合式（9）和式（14）～式（19c），式（12b）和（13b）可以表示为

如需借助式（11b）计算m值，需已知l/d。由图1可得

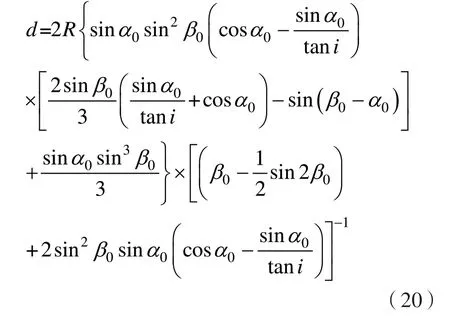
综上，对于同时考虑水平地震与竖向地震的均质粘性土坡的稳定安全系数可以表示为

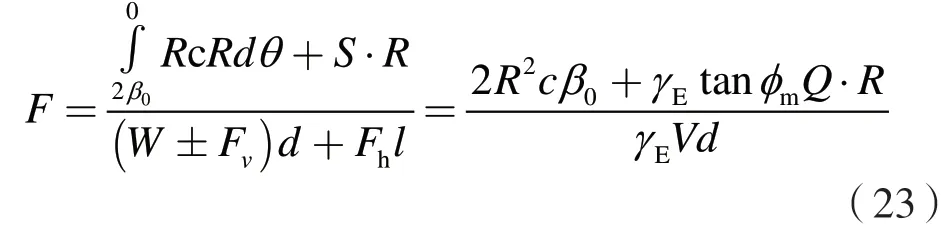
其中，由图1所示的几何关系易得潜在滑动体的体积

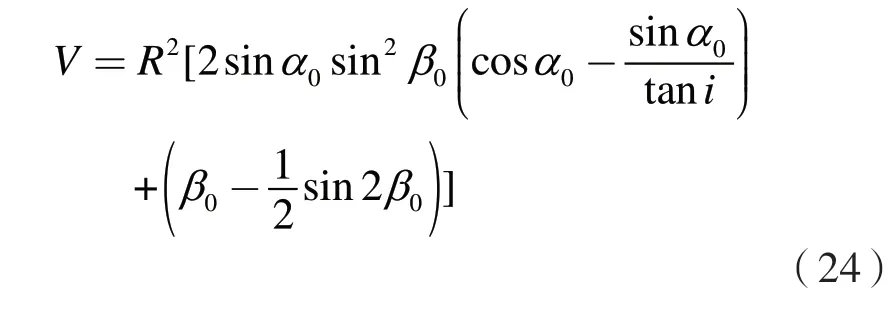
1.2 相关公式推导

本文引入抗震修正的内摩擦角φm、综合重度Eγ代替γ，而根据传统泰勒稳定图，当土体内摩擦角φ保持不变时，稳定数c/FγH和边坡倾角i是一一对应的。因此在改进后的泰勒稳定图中，φm一定时，稳定数c/FγEH和边坡倾角i也是一一对应的。在实际应用过程中可将φm、γE分别代替φ和γ，再根据传统稳定图确定即可。

图2所示为均匀黏质土坡稳定安全系数的求解过程。首先，借助图1可求解出潜在圆弧滑动面对应圆柱的半径R，然后由式（17）以及式（18）求解出潜在圆弧滑动面的圆心O(h,k) ；式（20）以及式（21）求解出潜在滑动体水平力臂d以及竖向力臂l；式（12c）、式（13c）以及式（22）求解出相关的过程参数P、Q、l/d；再由式（11b）以及式（6）求解出抗震修正内摩擦角φm以及综合重度γE；最后可由式（23）或查泰勒稳定图来最终求解边坡稳定安全系数。

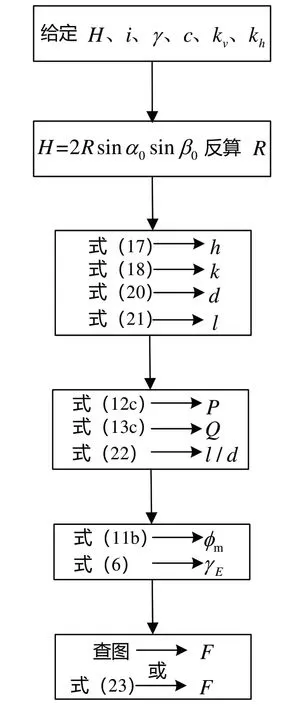
图2 计算稳定安全系数流程

2 有限元验证

国外很多边坡解析法研究工作均是建立在图3所示的边坡基础上的，考虑到该边坡的验证工作比较充分，因此本文也采用该边坡。均质的土坡，为粘性土，坡高为H=10 m，坡角I=45°，土体的重度γ=20 kN/m3，内摩擦角φ=20°，粘聚力c=12.38 kPa。

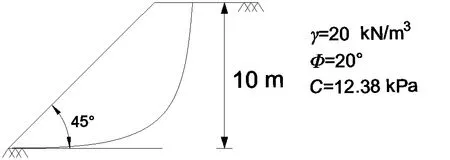
图3 验证模型及参数

针对图3中的边坡数值，借助强度折减法（郑颖人和赵尚毅,2004；王冬勇等,2019）对其进行模拟及分析，以此来对本文所提出的改进方法的有效性进行验证。强度折减法总的思想是对土体的强度粘聚力和内摩擦角进行不断折减，直至计算不稳定为止。考虑到综合研究水平与竖向地震作用是具备普适性的，而其他情况仅为特殊条件下的特例，所以只需考虑对该情况进行数值模拟分析即可。模拟时本文采用的是C2D8平面应变单元。本构模型采用的是线弹性和Mohr-Coulomb模型。模型参数的取值具体为，弹模E为105kPa，泊松比ν为0.35，重度γ为20 kN/m3，内摩擦角φ=20°，粘聚力c=12.38 kPa。借助拟静力法施加水平及竖向地震作用，其中，水平及竖直地震作用方向分别选为远离边坡方向及竖直向下，水平及竖直地震系数分别取kh=0.25，kv=0.125。数值模拟时，持续折减粘聚力与内摩擦角到计算出现不收敛，具体的折减规则φ′=arctan(tanφ/Fs)和c′=c/Fs，F s为折减系数，且计算不收敛时Fs取得最大值，该最大值即为稳定安全系数。实际计算中，通过将稳定安全系数取值从0.5增大至2.0，即可得到如图4所示的塑性应变图。相应的，此时稳定安全系统取值为0.69。

图4 计算不收敛时的塑性区

将水平和竖向地震作用同时考虑在内时，按照本文所提出的改进方法所得到的边坡稳定安全系数是0.66，而按照有限元数值计算所得到的为0.69，两者差距仅为4.35%。这不仅说明本文提出的改进方法有效，且能说明其是偏安全的。

3 应用实例

仍以图3所示的边坡为例，考虑4种情况下的边坡稳定性：（1）不考虑地震作用，退化为传统泰勒稳定分析，取kh=kv=0；（2）只考虑水平地震作用，退化为Majumdar的改进稳定分析，取kh=0.25，k=0.0；（3）仅考虑地震竖向作用，取kh=0.00，kv=0.125；（4）水平和竖向地震作用，取kh=2kv=0.25。

按照图2所示的流程，结合相关参数容易得出4种情况对应的边坡稳定安全系数如表1所示。从表中可以明显的看出，当竖向地震作用竖直向下时相应的安全系数比竖直向上时相应的安全系数要小，这对设计工作而言是偏安全的，因此建议竖向地震作用取竖直向下。相对于只考虑水平地震作用，同时考虑水平及竖向地震作用时边坡稳定性更低，因此为了最大限度保证安全性，应适当考虑竖向地震作用。

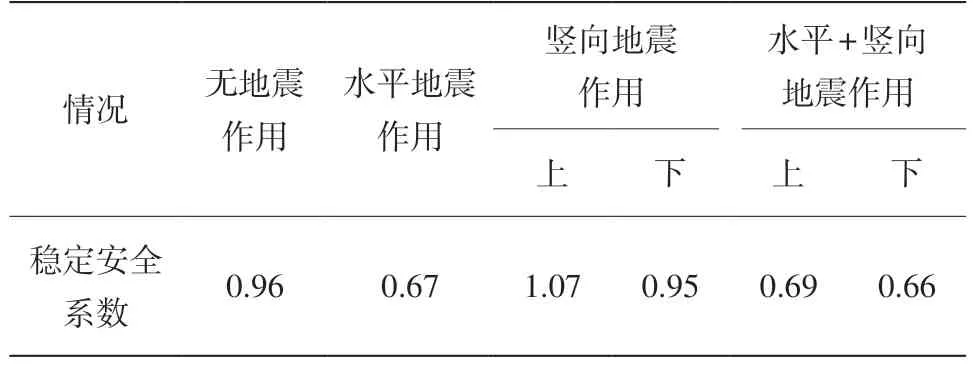
表1 简化方法计算结果对比表

为独立探究边坡稳定性受竖向地震作用的影响，如图3，借助前文提出的简化算法并将水平及方向竖直向下的竖向地震作用同时考虑在内，研究6度、7度、8度和9度时边坡稳定性（《建筑边坡工程技术规范》GB 50330-2013①；《建筑抗震设计规范（2016年版）》GB 50011-2010②,《公路桥梁抗震设计细则》JTG/TB 02-01-2008③），相关计算结果如表2所示。独立计算竖向地震作用是本研究的重点内容。因此在实际计算过程中，将水平地震作用考虑在内的同时保持抗震等级不同，并借助强度折减法使边坡处于临界失稳状态，安全系数为1.0。再保持土体强度一定，将水平及竖向地震作用同时考虑在内，重新对边坡稳定安全系数进行求解。于是，边坡稳定性所受竖向地震作用的影响就可由该安全系数与1.0之间的差值加以呈现。

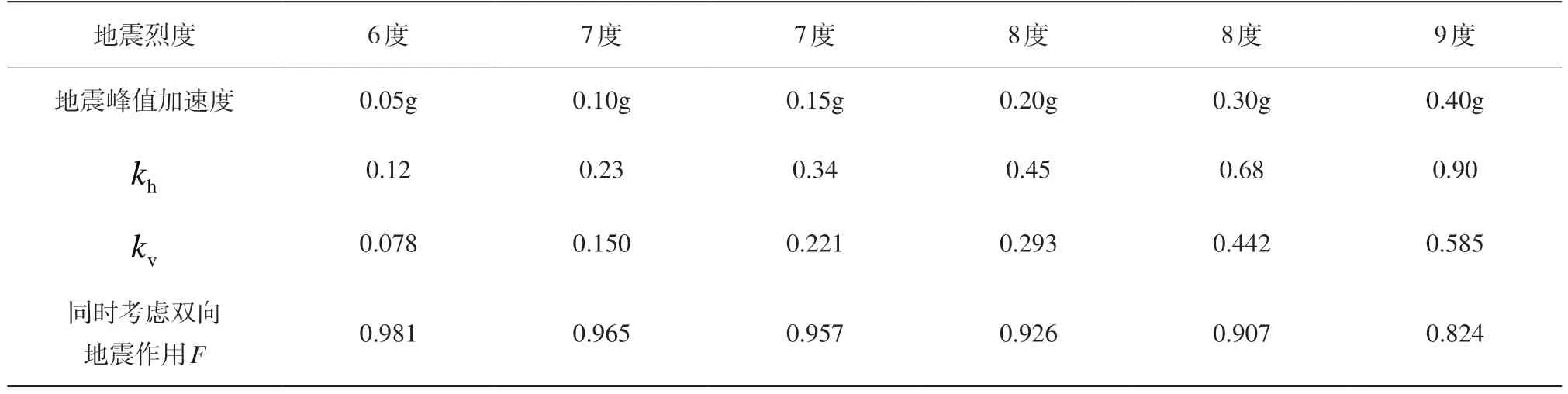
表2 各不同抗震等级下边坡安全系数表

如表2所示，表中各种情况下所得安全系数和1的差的绝对值就表示竖向地震作用对相应的边坡稳定性的影响。抗震等级与竖向地震作用对边坡稳定性的影响呈现出正相关关系。当对6度、7度设防时，竖向地震作用的影响在5%以内；当对8度设防时，影响在5%～10%之间；当对9度设防时，影响则最为显著，此时大于15%。综合以上论述，建议6度、7度时可忽略竖向地震作用影响，8度时则应加以考虑，9度时必须加以考虑。

4 结语

为同时将水平和竖向地震作用对边坡稳定性所产生的影响考虑在内，本文结合前人工作成果及必要理论推导最终给出改进边坡稳定计算方法，并进一步给出了改进边坡稳定图。同时，在对比分析了采用改进方法得出的计算结果和采用有限元数值计算方法得出的计算结果之后，形成以下4点结论：

（1）采用本文提出的改进方法，并结合拟静力法、泰勒边坡稳定性图以及水平、竖向地震系数等，能够实现对边坡稳定安全系数的简便求解。

（2）水平、垂直地震系数的数值越大，地震影响折减后内摩擦角越小，边坡稳定性越弱。

（3）相对于只考虑水平地震作用，同时考虑水平及竖向地震作用时稳定安全系数会更低，因此应适当考虑竖向地震作用。

（4）竖向地震作用取竖直向下对相应的设计工程而言更加安全，8度需考虑竖向地震作用影响，9度时必须考虑其影响。

注 释

①中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局.2016.建筑抗震设计规范（2016年版）:GB 50011-2010[S].北京:中国建筑工业出版社.

② 中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局.2014.建筑边坡工程技术规范:GB 50330-2013[S].北京:中国建筑工业出版社.

③中华人民共和国交通运输部.2008.公路桥梁抗震设计细则:JTG/TB 02-01-2008[S].北京:人民交通出版社.