单元整体教学实证研究设计与实施

邬盼盼 杨红娟

“简易方程”是人教版数学教材五年级上册第五单元内容，在“实际问题与方程”板块学习中，学生往往会出现“不会设定未知数”“不会寻找等量关系”“列出两边有x的方程不会解”等问题。其中一个重要原因是教材板块之间有系统性缺陷，形成了学习难点。基于学生的学习难点，我们对“简易方程”单元进行整体教学重组并进行实证研究。

一、单元整体教学重组简述

1.“用字母表示数”板块

聚焦“未知数设定与未知数之间代入转换”。第一，降低学习起点，数量关系中不涉及函数关系。第二，把教材原有5个例题合并、削减为3个例题，放大“用字母表示特定未知数”含义，整体推进用字母表示一步运算和两级运算的数量关系。第三，每个练习题设计中重视未知数设定与代入、字母参与运算和代入求值等相关练习，开展相关训练。

2.“方程的意义”板块

将等量关系的理解与刻画作为“方程的意义”教学硬核。第一，在“方程的意义”教学中补充教学“等量”概念，利用含有“单价、路程、工作总量”（一定）的数量关系题组，引导学生理解在含有两个主角的情境中存在等量关系。第二，淡化形式化的方程定义，重视等量题组情境变式，在已知数和未知数之间建立等式关系，以等量关系作为建立方程概念的主要线索。

3.“解方程”板块

依据等式性质扩展“两边含有未知数”的解方程技能。在教材解方程各种类型基础上，增加类似“10+3x=8x”“6x-36=2x”的方程拓展练习，抓住抵消与平衡的思想方法，逐步建立程序思维，基本学会解“两边含有未知数”稍复杂方程，为列方程解决问题扫清障碍。

二、研究基本思路说明

1.新序列实践研究说明

在区域内选取5所学校（城区3所、乡镇2所）进行实验对比研究，每所学校中选取水平相当的两个五年级平行班，分为对照班、实验班，样本学生共计385名。以整个单元为研究周期，对照班采用原序列、实验班采用新序列进行教学。整个单元教学结束后，对照班和实验班统一进行后测分析。针对不同学业水平等级的学生，把对照班、实验班的学生划分为待合格、合格、良好、优秀四个等级，人数占比分别约为10%、20%、25%、45%。

2.测查内容说明

学习水平测查分为用字母表示数、等式性质及解方程和用方程解决实际问题三个维度。用字母表示数侧重考查学生用未知数设定与代入、字母参与运算和代入求值的能力水平。解方程侧重考查学生运用等式性质灵活求解方程的能力。用方程解决实际问题侧重考查学生灵活运用方程解决问题的意识，以及综合运用未知数设定、用方程解决实际问题的能力。

三、后测数据分析

测查数据显示，“用字母表示数”“等式性质及解方程”“用方程解决实际问题”三个维度，实验班学生的正确率均高于对照班学生。具体表现在三个维度、六大优势：

1.在用字母表示数维度，实验班学生在用字母表示数维度具有更强的进行字母参与运算的能力。

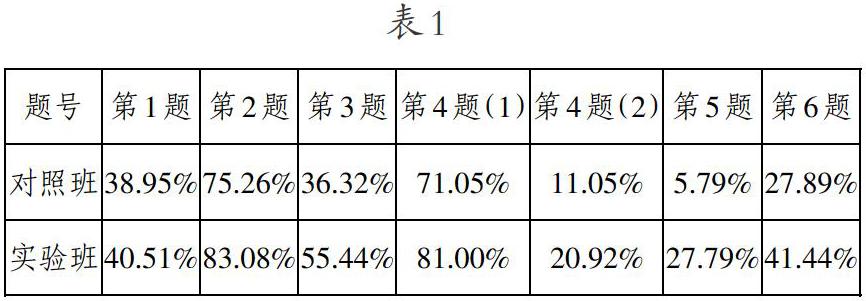
看图填空题，针对学生的答题情况，分别从能正确用含有字母的代数式表征数量关系、能用最简形式表示两个层面进行了统计，其中“数量关系正确”这一层面实验班相比对照班并无明显优势，但“能用最简形式表示”这组数据，可以看到实验班明显高于对照班，具体如表1。

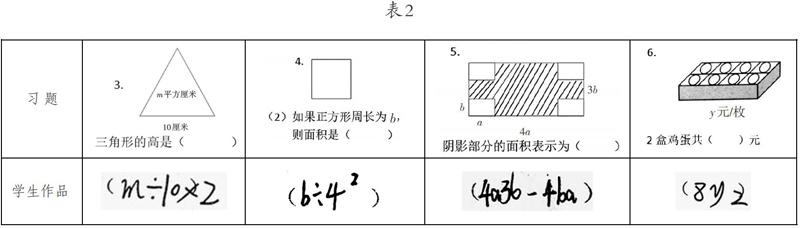
尤其是第3、4（2）、5、6这4道小题，实验班能够用最简形式表示结果的百分比明显高于对照班。学生错误的情况主要如表2。

以上4题需要学生具有较强的字母式运算的能力，如做习题3、6时，学生无法将数字与含有数字的代数式进行乘、除法运算的合并;做习题4（2）时，学生无法进行除法式的平方表征;做习题5时，学生无法将两个代数式进行乘法或减法运算合并。未化简的占比，对照班明显高于实验班，说明新序列的学习，增强了学生进行字母参与运算能力的培养与发展。

2.在用字母表示数维度，实验班学生具有更强的借助字母探索、表征规律的能力。

教师出示图1问题，将学生回答情况划分成四个水平层次，具体占比如表3。

从上表可以发现，实验班学生达到水平3的占了40.77%，而对照班学生仅5.26%，说明实验班学生借助未知數进行规律探索的能力大大高于对照班学生，新序列对帮助学生提高运用字母发现规律、探索规律的能力具有明显的优势。

3.在等式性质及解方程维度，实验班学生具有更强的应用等式性质的能力，说明新序列对于培养学生灵活应用等式性质的能力具有优势。

解方程维度测查题包括“根据等式性质填空”和“解方程”两大题，根据等式性质填空测查数据如表4。

从表4可以看出，3道习题实验班的正确率均高于对照班，尤其是第2题，在难度加大、正确率偏低的情况下，实验班学生显示出了明显的优势。学生的主要错误如表5。对于关系较为复杂、需要多次运用等式性质进行转化的题目，学生有一定的困难，而实验班学生在转化关系复杂、含有多个字母的等式时更加具有优势。

4.在等式性质及解方程维度，实验班起点较低的学生正确率明显高于对照班，显示了新序列在低起点学生掌握解方程技能上发挥了显著优势。

解方程共8道习题，包含了本单元中涉及的各种类型，按学生的学业水平层次，分待合格、合格、良好、优秀四个层次对答题情况进行了统计，具体如表6。

从表6可以看出，在解方程能力上实验班良好和优秀水平层次的学生并未显示出明显优势，但是待合格、合格水平层次的学生，正确率明显高于对照班学生，其中（4）8x÷0.6=2.4、（5）6x+1.2×4=9.6、（7）1.2x+0.6x=36这三道题，实验班这两个水平层次的学生均高出对照班10个百分点以上，说明新序列更加符合学生学习解方程技能的序列，对低起点学生掌握解方程技能具有优势。

5.在用方程解决实际问题维度，实验班学生使用方程来解决实际问题的意识更强，更加主动地选择方程来解决实际问题。具体数据如图2。

从图2可以看出，实验班学生主动使用方程解决问题的意识明显高于对照班学生，3题占比相差均在15%左右，其中第3题相差最多，实验班比对照班高了近20%。

6.在用方程解决实际问题维度，实验班学生能更加灵活地根据信息设定未知数，方法更加多元，说明新序列对培养学生合理设定未知数的能力上具有优势。

测查题中提供了如下习题：王老师从家骑车去学校上班，如果每分钟行150米，就要迟到6分钟;如果每分钟行200米，就比上班时间早1分钟到达。王老师家与学校相距多少米？

用方程解答此题时，对照班有95.34%的学生都是将“王老师家与学校的距离”设为未知数x，而实验班学生有75.26%的学生将“王老师所需时间”设为未知数x，另有24.74%的学生将“王老师家与学校的距离”设为未知数x。说明实验班学生能更加灵活地根据信息选择合适的量作为未知数，方法更加多元，能更好地建立等量关系，进而解决问题。

基于以上数据，可以看到新序列的学习路径在“用字母表示数”“等式性质及解方程”“用方程解决实际问题”三个维度都较大程度地提高了学生的学习能力水平，针对起点较低的学生，新序列能够帮助学生更好地掌握解方程技能。但是在数据中我们也发现，虽然实验班学生正确率占比高于对照班，可整体正确率还是偏低，如用字母表示数维度中，学生正确化简的占比较小，说明同时包含数字及字母的合并运算可以进一步强化;又如，学生在信息量复杂的实际问题中找到等量关系列出方程的能力，也有待进一步提高，这也是后续优化本单元学习路径可以努力的方向。

（作者单位：浙江省宁波市奉化龙津实验学校 浙江省宁波市奉化区尔仪小学）