前白枣山铁矿地面爆破振动预测*

黄玉华，张海军，徐国权

(1.青龙满族自治县发达矿业有限责任公司，秦皇岛 066000；2.东华理工大学 地球科学学院，南昌 330000)

岩石开挖是采矿、隧道和土建工程中最为重要的工作环节之一。在上述工程当中，爆破是最为经济有效的岩石破碎手段，并得到了广泛的应用[1]。特别是在采矿工程领域，爆破对后续铲装、运输、破碎等环节的成本有着直接的影响。然而，在爆破破岩过程中，炸药爆炸所释放出的能量只有一小部分(20%～30%)被用于破碎和移动岩石，其余能量不可避免的会以地面振动、飞石、空气冲击波、噪声、粉尘和有毒有害气体等形式对周围环境造成不利影响[2]。在这些不利影响中，地面振动无疑是人们最为关注的，大量研究和工程实践表明，地面振动是引起周围结构变形、位移和破坏的主要因素。为此，研究人员在致力于提高爆破破碎效果的同时，也对爆破振动的控制进行了大量研究[3]，以避免生产爆破对岩体和附近的建筑物造成破坏。

为了控制爆破振动的危害，各个国家都制定了相应的标准[4]。因此，准确评估和预测爆破引起的地面振动已经成为许多矿山的基本要求。众所周知，地面振动受到各种因素的影响，可以把这些因素分为两大类，即可控的和不可控的，可控的因素主要有炸药参数(爆速、能量、密度等)、钻孔参数(孔深、孔径、倾斜角度等)和爆破设计参数(孔距、排距、起爆系统、起爆顺序、装药方式、堵塞，自由面数量等)；不可控的因素主要有岩石性质、地质条件等。一般来说，位移、速度和加速度中的任何一个都可以用来描述地面运动。其中，采用峰值质点速度(Peak Particle Velocity,PPV)来表示地面振动得到了广泛的认可[5]。

为了评估和预测爆破引起的地面振动。在早期的研究中，研究人员试图建立一个预报方程来预报地面振动。通过收集爆破振动数据，建立数学模型并找到数学模型中的系数，最后使用回归算法对模型进行校准。预测方程的系数反映了岩体特性的一般规律。绝大部分预测模型都是基于两个主要参数来进行预测的[6-9]，即最大单段药量和从爆破点到监测点的距离。经验模型在国际上得到了广泛的应用，并得到了爆破工作者的认可。然而，由于爆破影响因素的复杂性，经验预测模型还存在一定的缺陷，并不能适用于所有场所。

回顾最近的文献表明，影响PPV的参数复杂性可以通过引入人工智能(Artificial Intelligence,AI)技术来解决。这主要是AI技术在求解非线性连续函数方面的能力，已经在工程领域得到了广泛的应用和发展。在爆破振动预测方面，越来越多的研究人员尝试使用AI技术作为爆破振动的主要预测方法，以替代传统的经验模型，并取得了很好的预测效果。Khandelwal等人使用神经网络(Artificial Neural Network,ANN)模型对150次爆破事件的PPV和频率进行了预测[10]，结果表明ANN模型的结果具有很高的准确率。Danial Jahed Armaghani等人提出使用自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System,ANFIS)和ANN两种AI技术[11]，来对采石场爆破引起的地面振动进行预测。Fisne等人提出了一种基于模糊推理系统(Fuzzy Inference System,FIS)的预测模型对土耳其一家采石场的33次PPV监测数据进行了预测[12]，取得了很好的效果。Ghasemi等人提出了另一种模糊模型[13]，模型使用6种不同的可控输入参数。他们还强调了模糊模型在PPV预测方面的高性能。Hasanipanah等人引入支持向量机(Support Vector Machine,SVM)模型来评估PPV[14]。Manoj Khandelwal等人使用分类回归树(Classification And Regression Tree,CART)模型来对PPV进行预测[15]，结果表明CART技术在预测PPV方面比传统方法更可靠。Mahdi Hasanipanah等人提出了一个基于粒子群优化(Particle Swarm Optimization,PSO)算法的模型[16]，用于预测伊朗Shur River大坝区域爆破作业所引起的地面振动。Danial Jahed Armaghani等人尝试使用帝国主义竞争算法(Imperialist Competitive Algorithm,ICA)来对爆破振动进行预测[17]。Erlin Tian等人基于遗传算法(Genetic algorithm,GA)提出了两种新的智能模型[18]，用来模拟地面振动。近年来，各种智能算法广泛的应用到爆破振动预测领域，已经成为爆破振动预测的主要发展方向。

虽然利用AI技术对爆破振动预测进行一些研究，但没有一种方法或模型对每个矿山都是最优的。此外，AI技术是一种需要不断进化和多样化的方法。在此基础上，开发一种ANN模型来对前白枣山铁矿爆破振动进行了预测，并与传统经验模型和多元线性回归模型(Multiple Linear Regression,MLR)预测结果进行比较[19]。

1 场地条件和数据采集

现场测试是在发达矿业有限责任公司下属的前白枣山铁矿进行的。前白枣山铁矿位于河北省秦皇岛市青龙县朱杖子乡前白枣山村西南，矿区中心地理坐标为东经119°01′，北纬40°19′。矿区北西距青龙县城8 km。区内火成岩活动频繁，主要有花岗岩、伟晶花岗岩，其次有闪长岩、微晶闪长岩和少量煌斑岩脉侵入。脉岩对矿体起吞蚀分割破坏作用，使矿体沿走向及倾斜方向均遭到不同程度的破坏。

矿山采用浅孔留矿嗣后尾砂胶结充填采矿法，爆破作业使用YT-28型凿岩机打上向倾斜炮孔，炮孔直径40 mm，孔深1.8～2 m，最小抵抗线0.6～0.7 m，炮孔采用平行排列或交错排列，网度为0.7～1 m×0.7～1 m。炸药使用的是乳化炸药，非电导爆管起爆。

对之前地面振动预测研究的回顾表明，单段最大药量和爆破点到监测点的距离对PPV的影响均大于其它可控和不可控参数。以29组爆破作业的最大单段药量(MC)和爆破点到监测点的距离(D)作为预测PPV的指标，使用的数据及其范围如表1所示。

表 1 爆破振动数据

2 振动预测

2.1 经验模型

为了控制爆破振动的危害，不同的研究人员根据经验制定了各自的比例距离(Scaled Distance,SD)关系。SD是在双对数坐标轴上记录不同距离的PPV，并进行回归分析，如图1所示。本研究中使用4种在世界范围内较为常用的经验预测模型，并通过绘制PPV与SD在双对数坐标轴上的回归曲线，得到了4种经验模型的场地系数k和b，如表2所示。

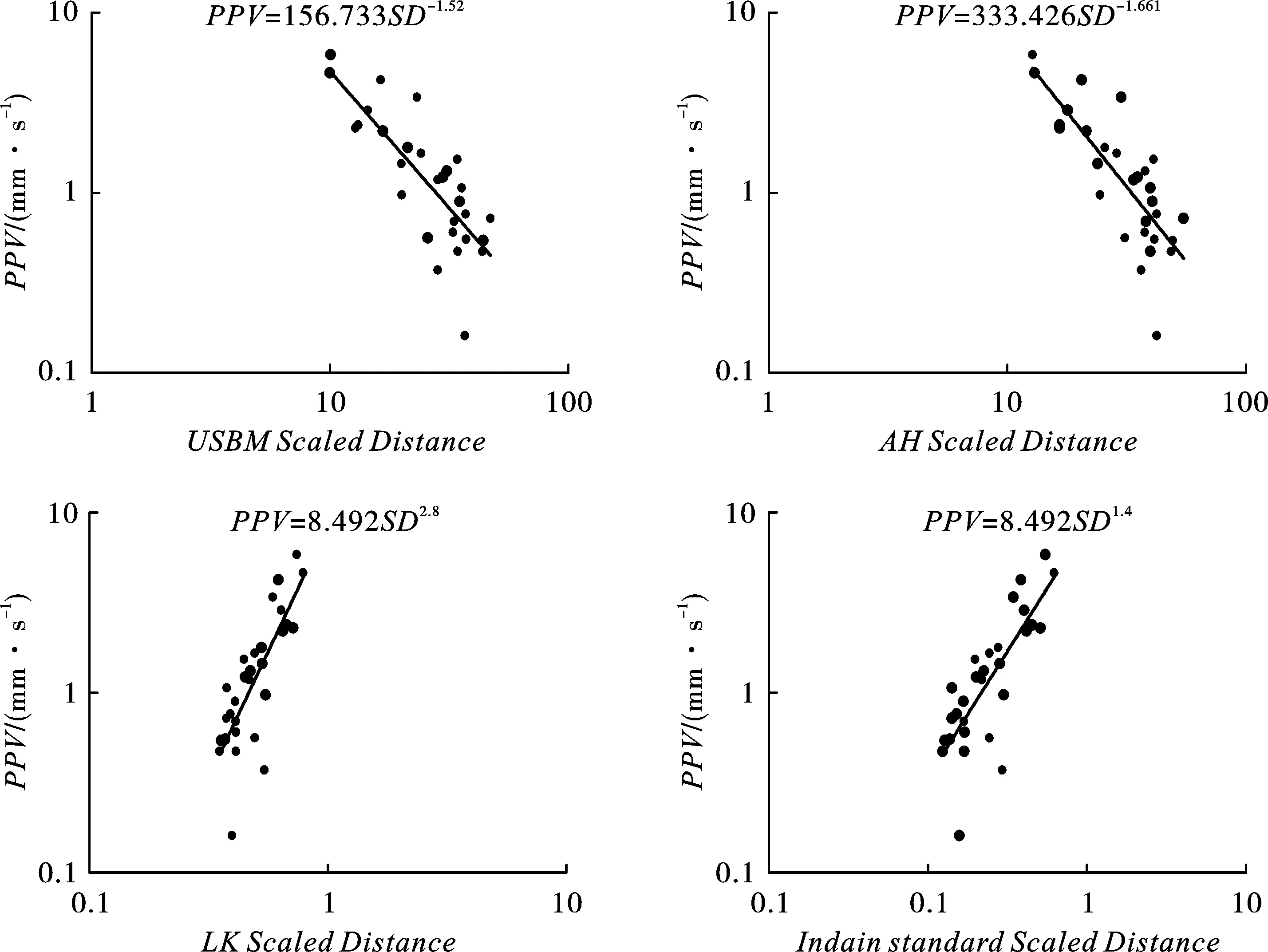
图 1 经验模型PPV和SD双对数图Fig. 1 Log-log plots between PPV and scaled distance for various models

图2给出了不同经验模型的预测值与实测值之间的相互关系。在本研究中，4种经验模型的确定系数(Coefficient of determination)R2分别为0.74、0.74、0.72和0.72，USBM模型和AH模型的R2相同，且预测能力要优于LK模型和Indain模型。

2.2 MLR

回归分析是一种统计工具，用来确定变量之间的关系。多元线性回归(Multiple Linear Regression,MLR)是通过对两个或两个以上的自变量与一个因变量相关分析，建立预测模型进行预测的方法。MLR是基于最小二乘法，这意味着MLR拟合使预测值和实测值的差的平方和最小。在建立MLR模型时，使用MC和D作为模型的输入参数来对PPV进行预测，MLR可以表示为

表 2 经验模型场地系数

Y=β0+β1X1+β2X2+…+βkXk+ε

(1)

式中：Y是预测变量；Xk为自变量；βk为回归系数；ε为随机误差。计算得到

PPV=2.182-0.052D+0.579MC

(2)

图3给出了MLR模型预测值与实测值之间的关系，R2为0.637。

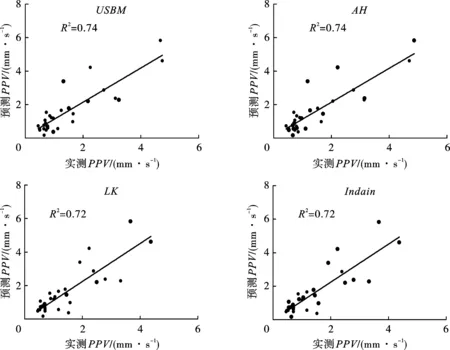
图 2 经验模型测量值和预测值对比图Fig. 2 Measured vs.predicted PPV values of the Empirical model

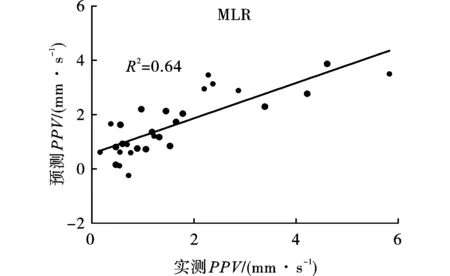
图 3 MLR模型测量值和预测值对比图Fig. 3 Comparison between measured and predicted PPVs by MLR model

2.3 ANN振动预测

ANN是20世纪80年以来在人工智能领域兴起的研究热点，也是目前最先进的AI技术之一。ANN起源于人类大脑的生物结构。ANN模型是由被称为神经元的细胞构成，树突从细胞体延伸到其它神经元，每个神经元都能接受、处理和传输信号。因此，ANN工作建立了输入和输出之间的关系。它可以从输入和输出数据之间的因果关系中学习，适用于求解存在多个非线性关系参数或变量间某些相关关系不易识别的复杂问题。ANN计算通常分为三个步骤，首先需要确定网络架构，接下来是进行训练，最后进行检验。

神经元的排列决定了ANN的结构，其中最常用的是多层感知(Multi-Layer Perceptron)技术。ANN中的神经元数量是有限的，它们分布在输入层(输入数据)、隐藏层和输出层(计算数据输出)中，如图4所示。经过训练，ANN通过调整神经元之间的数值比率来完成特定的功能。这里较为常用的是反向传播(Back-propagation,BP)算法，BP算法有一个输入层和一个输出层，一个或多个隐藏层，其中权值(w)和偏差(b)在学习过程中被拟合，并分配给神经元之间的连接。

图 4 反向传播网络算法爆破设计模式Fig. 4 Network back propagation algorithm for design pattern of blasting

对于ANN技术，最关键的问题是ANN设计。在本研究中，设计了一个包含训练算法、隐藏层和每个隐藏层中的神经元的ANN。在设计ANN时，最具挑战性的问题是确定隐藏层的数量和每个隐藏层的神经元数量。理论上，只有一个隐藏层的ANN可以解决实际中的大多数问题。两个或更多隐藏层的ANN可以根据情况更好的解决问题。然而，过多的隐藏层会增加ANN的处理时间。因此，本研究采用单一隐藏层构建ANN。利用ANN作为函数逼近工具，选择预测PPV最有效的两个变量MC和D作为输入变量。由于BP算法存在固有的缺陷，Levenberg-Marquardt算法可以有效克服BP算法的缺陷。为此需要对数据进行预处理，即对数据进行归一化，隐藏层函数为sigmoid，输出层函数为purelin。

为了训练ANN，在采集到的29组数据中，21组数据用于训练，4组数据用于测试，4组数据用于验证。选择单一隐藏层，开发了8个ANN预测模型，隐藏层神经元个数依次为3～10，最大训练次数为1000次，训练目标最小误差为1e-6。利用Matlab软件来实现ANN，通过训练数据得到权值和偏差，同时选择测试和验证数据来确定网络的准确性和有效性。停止后，根据网络的训练过程和测量精度，得到最终的输出，并测试ANN模型的精度。验证结果表明，ANN能够很好的进行非线性回归分析。使用R2和均方误差(Mean Squared Error,MSE)来评价每个ANN模型的性能。表3给出了每个ANN模型的计算结果。结果表明，每个ANN模型的性能参差不齐，本研究中结构为2-6-1的ANN模型最适合用于进行PPV预测。图5给出了结构为2-6-1的神经网络模型的相关系数，包括训练、测试、验证和全部数据，且每一部分的相关系数R(Correlation coefficient)都大于0.92。

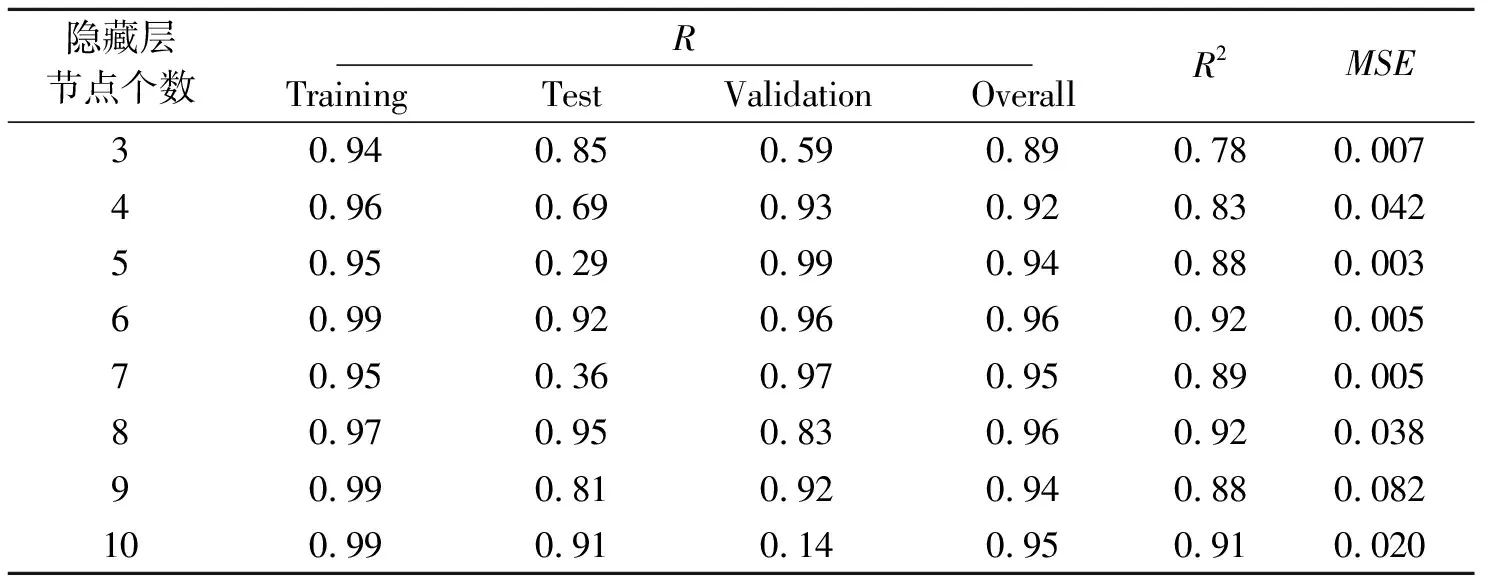
表 3 每个ANN模型的计算结果

图6给出了ANN模型预测PPV和实测PPV之间的关系。可以看到结构为2-6-1的ANN模型R2为0.92。ANN模型预测值非常接近于实际值，且模型的预测精度可以让人接受。

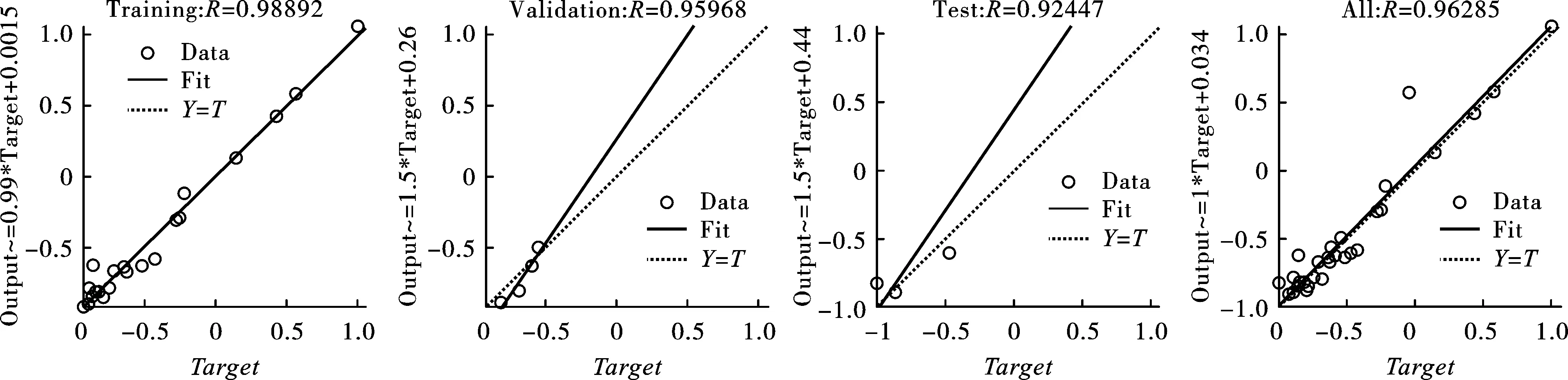
图 5 训练、测试、验证和全部数据的相关系数Fig. 5 Coefficient of correlation for the training,testing,validation and overall data sets

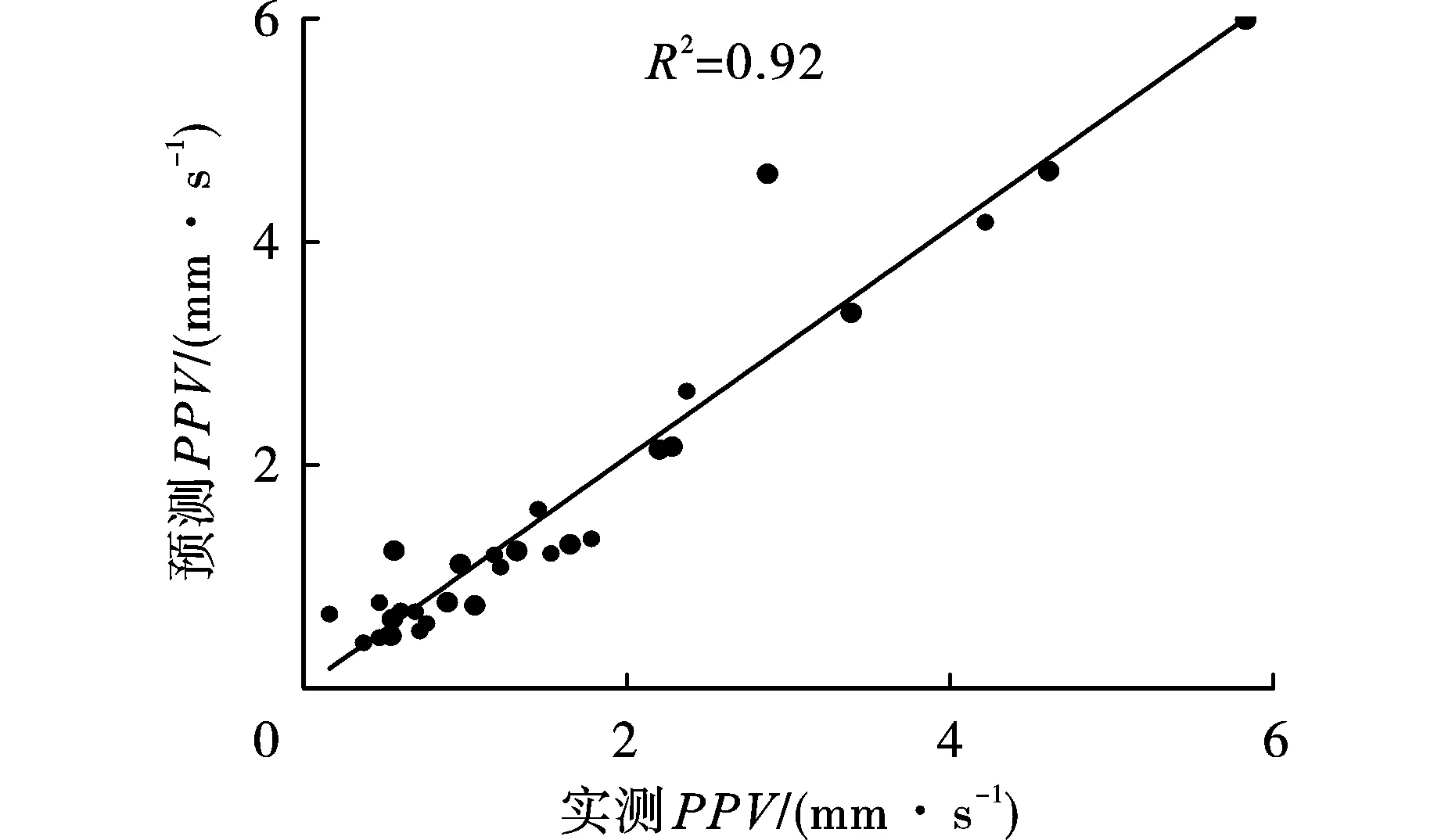
图 6 ANN模型预测结果与实测结果的关系Fig. 6 Graph between measured and predicted PPVs by ANN model

3 性能评价指标

为了比较和评价经验、MLR和ANN模型的性能，选择均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)和R2作为评价指标。RMSE、MAE和R2可以表示为

(3)

(4)

(5)

4 预测模型比较

确定ANN预测模型满足要求后，通过式(3)～式(5)对4种经验模型、MLR模型和ANN模型的性能进行评价。经验模型、MLR模型和ANN模型的预测性能如表4所示。可以看到，在本研究中使用，MLR模型的预测性能最低，其R2为0.64、RMSE为0.81、MAE为0.61，输入变量的线性关系关系不明显。由于监测数据有限，因此MLR模型在PPV预测中并未表现出很好的结果。

USBM、AH、LK和Indain等4种经验模型预测效果相差不大，USBM和AH模型性能稍好于LK和Indain模型。大量文献表明，USBM、AH、LK和Indain模型是世界范围内应用较为广泛的经验模型，已经在世界各地成功的进行了许多研究。然而，经验模型的有效性还没有得到很好的评价。

对于所建立的ANN模型，可以看到，与传统经验模型和MLR模型相比，ANN预测数据更接近真实数据，ANN模型的R2为0.92、RMSE为0.4、MAE为0.23。计算结果表明，提出的ANN模型在PPV预测方面是可以的，模型具有较高的预测精度。

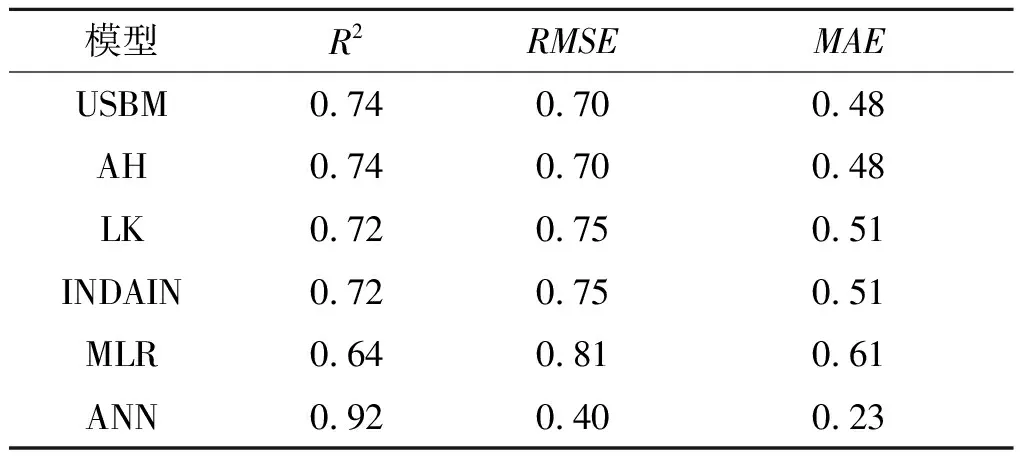
表 4 预测模型性能

5 结论

爆破是采矿工程的重要组成部分。然而，爆破产生的负面效应，特别是爆破振动，对周围环境有着很大的影响。因此，准确预测PPV在减小爆破振动方面起着重要的作用。分别使用4种经验模型、MLR模型和ANN模型对PPV进行了预测。结果表明，由于数据量有限，MLR模型预测效果相对较差，R2为0.64；4种经验模型预测结果较为接近，R2分别为0.74、0.74、0.72、0.72；提出的结构为2-6-1的ANN模型预测结果最接近实际监测结果，R2为0.92、RMSE为0.4、MAE为0.23。研究证明了使用ANN预测露天和地下爆炸振动的可能性，这将确保地面振动强度可以控制在安全范围内，使矿山爆破作业安全、高效。