基于FDM的爆破振动信号时频分析*

王海龙，柏皓博，王晟华

(1.河北省土木工程诊断、改造与抗灾重点实验室 河北省寒冷地区交通基础设施工程技术创新中心，张家口 075000；2.北旺建设集团有限责任公司，承德 067400；3.河北省装配式建造与地下工程技术创新中心，承德 067400)

目前，隧道掘进最常用的破岩方式为钻爆法，爆破开挖中产生的爆破振动势必会对周围岩体或建筑物的安全稳定性造成影响。而山岭隧道爆破振动效应经过复杂岩土体传播后，爆破振动信号更为复杂，给能量分析带来不便。爆破振动特征作为分析工程爆破影响的基础，对爆破振动信号进行时频分析，提取爆破振动特征具有重要意义。

爆破振动信号具有瞬时性、震荡性与突变性，表现为典型的非平稳信号，针对此类非平稳信号的分析，近年来使用较为广泛的方法有EMD(empirical mode decomposition)方法[1]、EEMD(ensemble empirical mode decomposition)方法[2]、CEEMDAN(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)方法[3]、小波方法[4]、小波包方法[5]。

EMD方法是一种基于瞬时频率的信号分析方法。它直接将信号在时域上进行模态分解，分解过程中保留信号本身特征。但会存在一个模态分量中包含不同频率的信号，或同一个频率信号被分解到不同模态分量中的问题，即模态混叠现象。为解决这一问题，EEMD方法、CEEMDAN方法被相继提出。EEMD方法通过在原始信号中加入正态分布的高斯白噪声，使信号自动分布到合适的参考尺度，从而降低模态混叠现象，但不可避免地会产生噪声残留问题。CEEMDAN方法自适应加入高斯白噪声，且在分解过程中得到各阶模态分量时均进行总体平均计算，从而缓解了噪声残留问题。但此类方法均未在根本上解决模态混叠问题。

小波分解会将小波系数较小的细节成分消除，有可能会丢失信号中有用信息，且主要针对信号低频部分进行分析，而小波包分解在此基础上可以同时对信号高频部分进行分析。但二者均受制于小波基函数与分解层数的选取，不同的参数对分析结果影响较大。

鲁超等利用EMD方法与小波分析对井下深孔爆破振动信号提取信号主分量[6]，进行后续分析。韦啸等利用EEMD方法对地铁隧道爆破振动信号进行降噪处理[7]，取得良好效果。王海龙等利用CEEMDAN方法与小波包分析联合方法对爆破振动信号进行降噪处理[8]，结果表明:CEEMDAN方法可以更有效缓解模态混叠现象。林大超等应用小波变换方法对短时非平稳爆破振动过程提出了时频特征分析[9]，发现基于小波变换的爆破振动时频特征分析相较于传统频谱分析方法可以给出更为准确的细节信息。单仁亮等利用小波包分析对爆破振动信号能量衰减特征进行研究[10]，结果表明利用小波包变换有利于信号的精确分析。

傅里叶分解方法(Fourier Decomposition Method)近年来被广泛用于信号分析领域[11-13]。因其分解完备性、正交性、自适应性，对于非线性、非平稳信号分析具有显著的优越性。

基于以上研究，引入一种基于FDM的隧道爆破振动信号分析方法。FDM基于傅里叶变换理论，可有效解决模态混叠问题，提高信号分析精度。比较EMD、EEMD、CEEMDAN、FDM的仿真信号分解结果，分别计算能量占比，对比分析四种方法模态混叠程度；对EMD、EEMD、CEEMDAN、FDM分解所得模态分量进行Hilbert变换，比较三者时频分辨率。最后将FDM应用于实测信号中，得到实测信号时频谱，所得时频谱可精确表示爆破振动信号低频部分特征，对爆破振动控制具有重要意义。

1 原理阐述

1.1 FDM理论

Pushpendra Singh等学者在傅里叶变换的基础上，提出一种新的时频分析方法，其可用于分析非线性、非平稳信号，即FDM，此方法通过在傅里叶域内自适应搜寻解析傅里叶固有频带函数(AFIBFs)，从而获得一系列傅里叶固有频带函数(FIBFs)和一个残余分量，获得多分量信号作为常数和单分量信号的唯一表示，该数学模型可用下式表示[14]。

(1)

式中：n(t)为残余分量;yi(t)∈C∞[a,b]为傅里叶固有频带函数(FIBFs)。

在搜寻AFIBFs时，可以由高频向低频搜寻(HTL-FS算法)，也可以从低频向高频搜寻(LTH-FS算法)，具体步骤为[15]：

LTH-FS算法

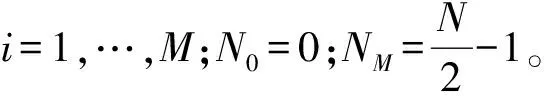
(1)对原始信号x(t)进行傅里叶变换，即X[k]=FFT{x[n]}；

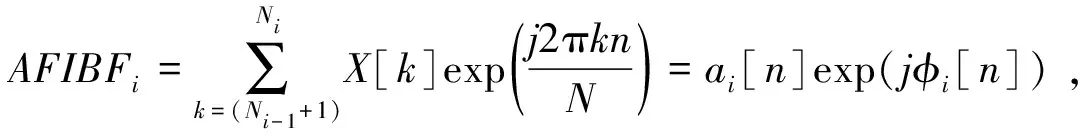
(4)对AFIBFs可求瞬时频率和瞬时幅值，AFIBFs的实部即为FIBFs。

HTL-FS算法

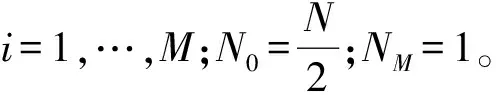
(1)对原始信号x(t)进行傅里叶变换，即X[k]=FFT{x[n]}；

(4)对AFIBFs可求瞬时频率和瞬时幅值，AFIBFs的实部即为FIBFs。

1.2 Hilbert变换

利用Hilbert变换可求取Hilbert谱，即时频谱，可表示幅度在时域与频域上的分布，得到时间-频率-能量三者之间联系。时频谱表达式为[16]

(2)

式中：Re为实部；i=1,2,…,n为模态分量个数；ai(t)为幅值函数；ωi(t)为频率函数。

1.3 能量占比

由于爆破振动能量主要集中于信号的低频部分，将爆破振动信号分解到不同频率带上后，若无模态混叠现象，低频模态分量与高频模态分量所占能量应有明显区分，故引入能量占比的概念，利用其来判别信号分解模态混叠程度。

通过对信号进行模态分解，可以得到n个模态分量，将残余分量忽略不计，所有模态分量能量之和应恒等于原始信号能量。则能量占比定义为[17]

(3)

式中：Ei为分解所得第i个模态分量能量；E为信号总能量。

2 数值仿真

2.1 仿真信号构造

利用正弦函数与余弦函数叠加来构造爆破振动仿真信号[18]，并加入信噪比为-2的高斯白噪声模拟由施工现场复杂工序交织进行产生的高频噪声，仿真信号如图1所示。

图 1 仿真信号波形图Fig. 1 Waveform of simulation signal

2.2 仿真信号模态分解

分别对含噪仿真信号进行EMD分解、EEMD分解、CEEMDAN分解、FDM分解。分解结果如图2所示。含噪仿真信号经EMD分解得13个模态分量与1个残余分量；经EEMD分解得13个模态分量与1个残余分量；经CEEMDAN分解得12个模态分量与1个残余分量；经FDM分解得到37个FIBFs，由于篇幅限制，展示FDM分解所得13个模态分量。图中r表示信号分解所得残余分量。

由图2可知，当信号中存在高频噪声时，EMD分解、EEMD分解、CEEMDAN分解所得分量高频部分模态混叠现象严重，低频部分相对较为稳定，但仍存在模态混叠问题。FDM分解所得模态分量由低频至高频依次排列，并未出现模态混叠现象，且由于未引进高斯白噪声辅助分析，故无噪声残留。

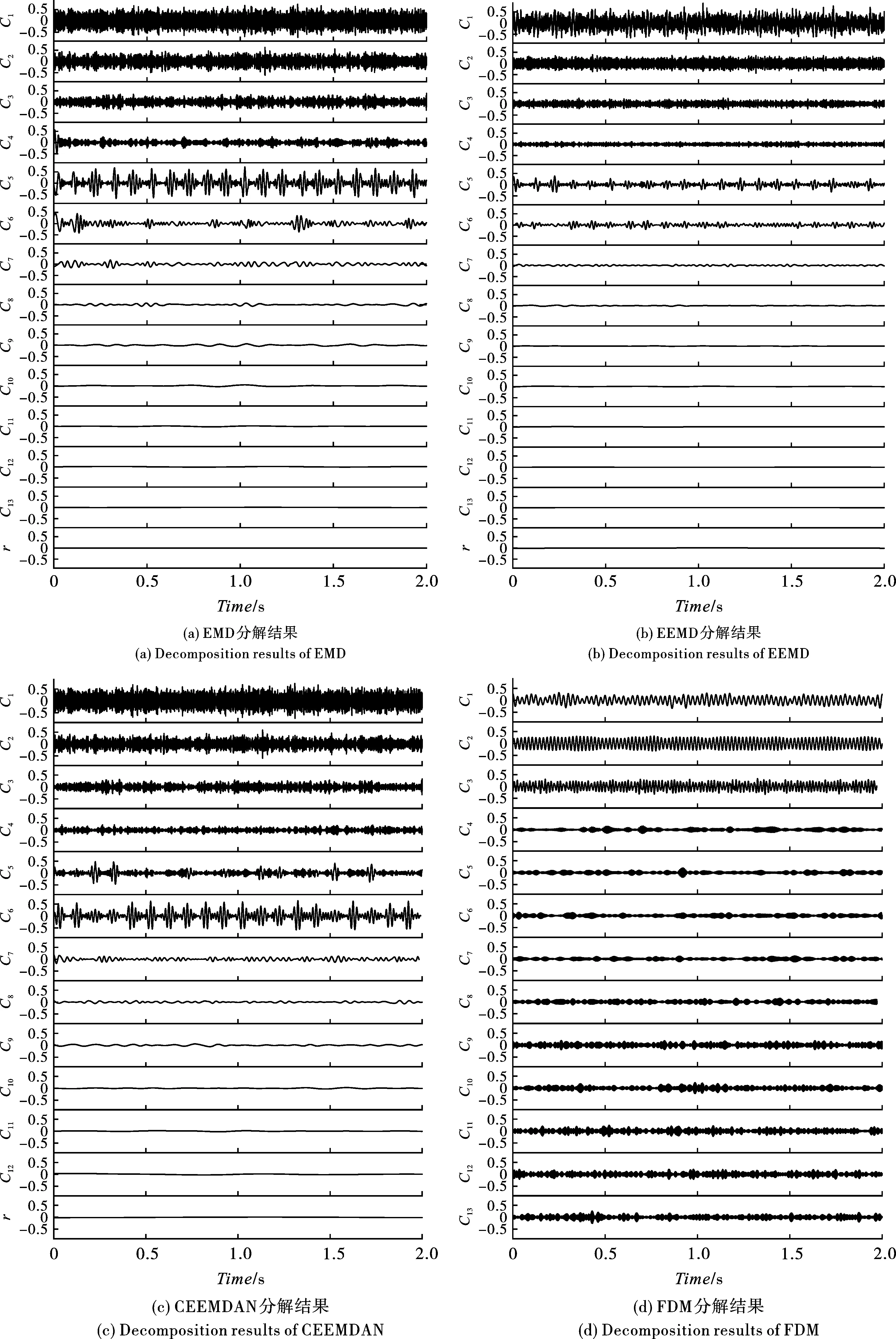
图 2 仿真信号不同方法分解结果Fig. 2 Decomposition result of simulation signal with different methods

2.3 模态分量能量占比

分别计算EMD分解、EEMD分解、CEEMDAN分解、FDM分解所得模态分量能量占比，计算结果如表1所示。由于篇幅限制，展示FDM分解所得13个模态分量的能量占比。

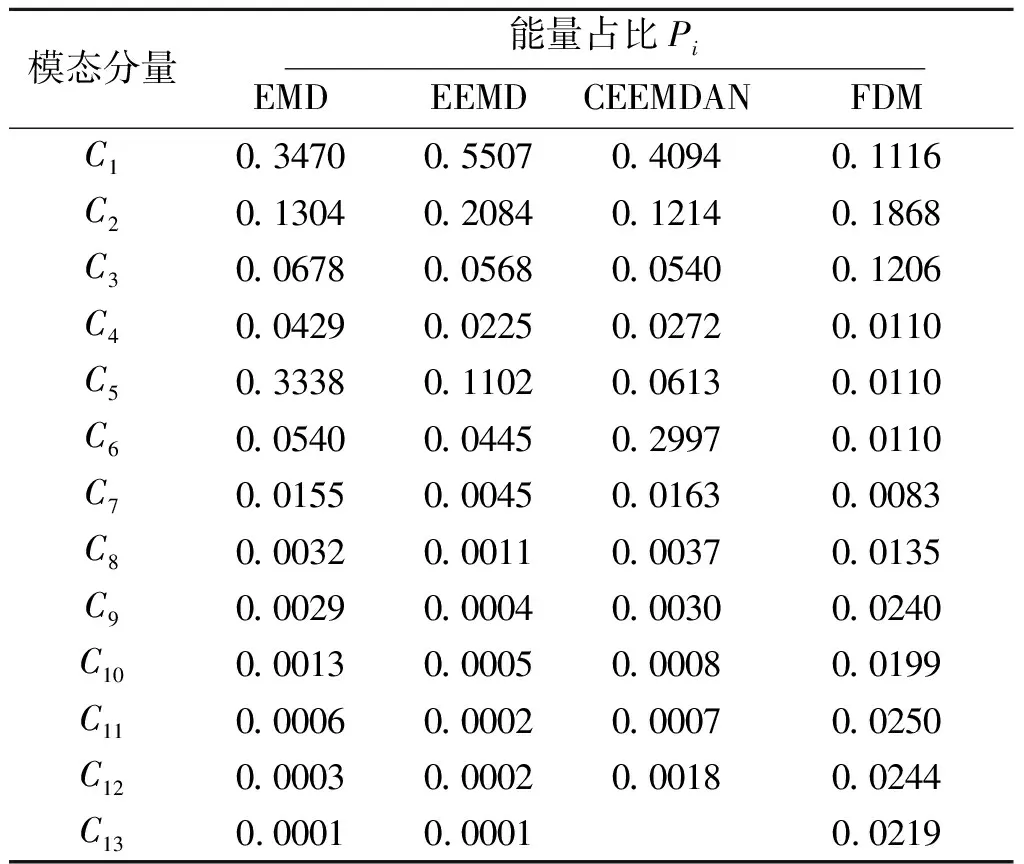
表 1 不同方法所得模态分量能量占比

将表1计算结果与图2一一对应，可以发现，EMD分解、EEMD分解和CEEMDAN分解高频部分模态混叠现象严重，且分解所得模态分量能量占比混乱，高频部分能量占比较高。而爆破振动信号能量主要位于信号低频部分[19]，故此三种方法对爆破振动信号分析不利。FDM分解所得模态分量低频部分占比较高，且主要位于前三个分量之中，与高频部分能量占比具有明显区分，说明模态混叠现象得到有效消除，对信号分析极为有利。

2.4 仿真信号Hilbert变换

利用matlab中互相关系数函数(corrcoef)计算FDM分解所得模态分量与原始信号相关系数如表2所示，结合能量占比筛选出前三个分量为信号有用信息，将其重构，重构波形图如图3所示。

表 2 部分FIBFs与原始信号相关系数

图 3 重构信号波形图Fig. 3 Waveform of the reconstruct signal

重构信号基本保留了纯净信号的峰值振速与局部特征，对其进行时频分析可以有效剔除噪声干扰，获得更为精确的时频信息。

利用Hilbert变换求得EMD、EEMD、CEEMDAN和FDM分解所得分量的时频谱,如图4所示。

当信号中含有高频噪声分量时，EMD、EEMD、CEEMDAN分解方法通过Hilbert变换获取所得时频谱图高频部分模态混叠现象严重，同时影响低频部分信息提取，分辨率不佳。EEMD方法低频部分模态混叠严重是由于在分解时添加了正态分布的高斯白噪声辅助分析，造成了噪声由高频传递到低频的问题。爆破振动能量主要居于信号低频部分，当信号中存在高频噪声时，使用此三种方法进行时频分析，不利于获取准确的信号特征。FDM分解后可准确获取信号低频部分能量分布特征，且根据信号波形图可以发现，经FDM处理后，原始信号中有用信息得以有效保留，在最大程度上保证了信号分析的准确性，适用于爆破振动信号。

3 实测信号分析

3.1 工程概况

依托太锡铁路太崇段新建崇礼隧道下穿和平村工程，新建崇礼隧道位于河北省张家口市崇礼区西湾子镇黄土咀村至崇礼区西湾子镇大夹道沟的崇山峻岭中，崇礼隧道3#斜井小里程方向于DK65+500～DK65+800段下穿和平村，下穿段埋深约30 m。和平村房屋多为砖混建筑和毛石房屋，结构较差，围岩等级为Ⅲ级和Ⅳ级。崇礼隧道与村庄位置如图5所示。

3.2 爆破振动信号采集

为使爆破对村庄影响最小化，对爆破振动进行实时监测，监测设备采用中科测控公司出产的TC4850爆破测振仪。该爆破测振仪配有三轴向振动速度传感器，分别对应X方向、Y方向、Z方向。使X方向指向3#斜井小里程前进方向，Y方向垂直于X方向指向村庄内部，Z方向垂直于X方向与Y方向垂直向上。测点布置如图6所示，采集所得部分数据如表3所示。

图 6 测点布置示意图Fig. 6 Schematic diagram of measuring point layout

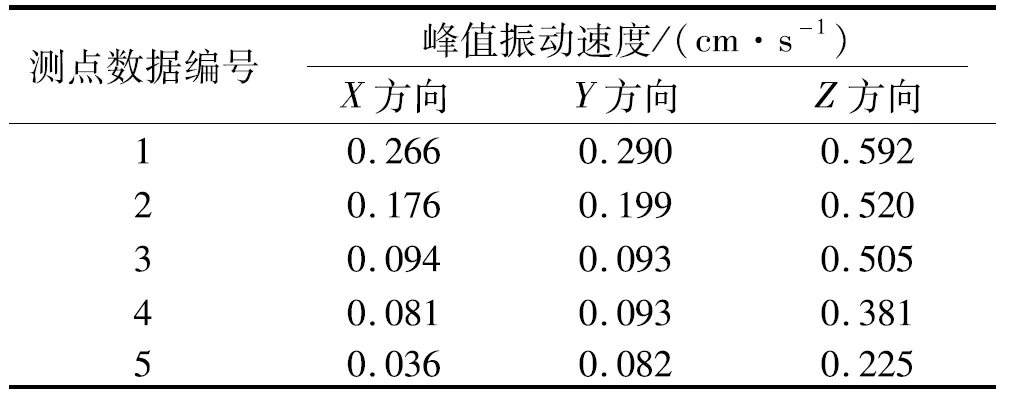
表 3 爆破振动速度数据

由表3可知本工程爆破振动对村庄的影响主要位于Z方向，选取Z方向爆破振动信号为研究对象。图7为某次爆破时采集到Z方向爆破振动信号，可以发现，受周围施工环境影响，爆破振动信号中含有高频噪声，对信号分析不利。

3.3 爆破振动信号时频分析

将实测信号进行FDM分解，由低频至高频得39个FIBFs和一个残余分量，由于篇幅限制，且爆破振动信号特征主要集中于中低频率带，故展示分解所得中低频部分10个FIBFs如图8所示。

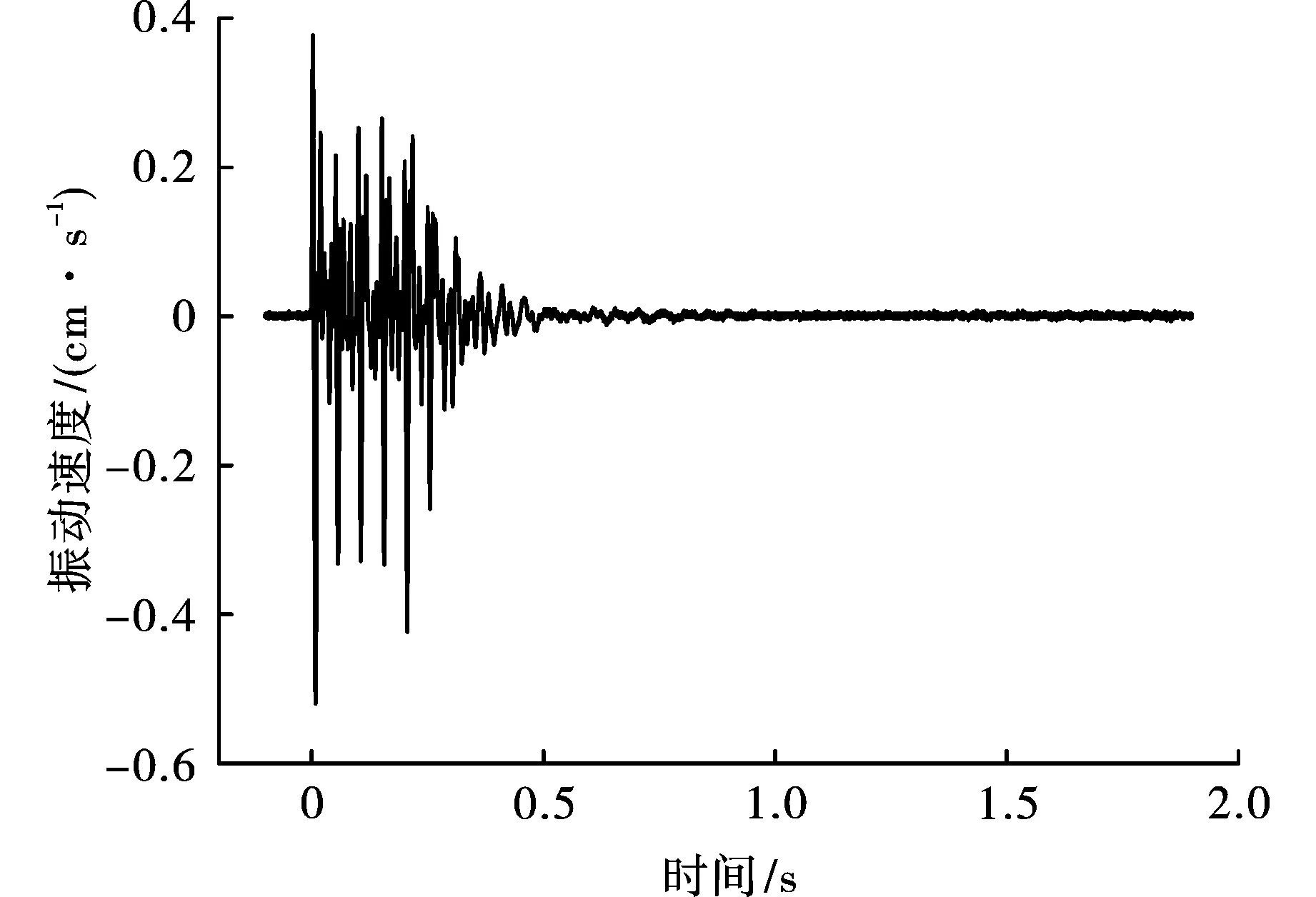
图 7 爆破振动信号波形图Fig. 7 Blasting vibration signal waveform

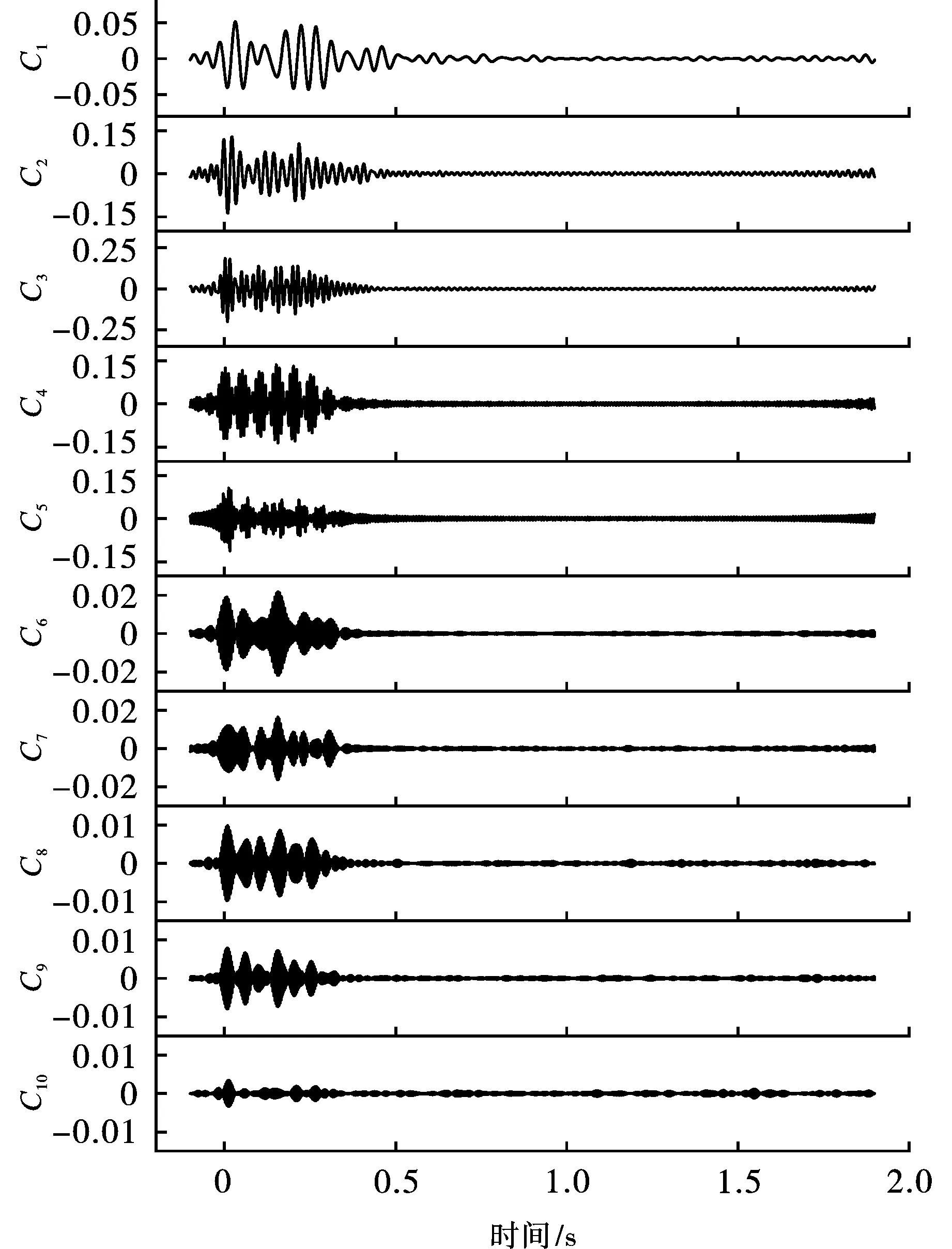
图 8 FDM分解结果Fig. 8 Decomposition result of FDM

利用matlab计算FIBFs与原始信号相关系数及其能量占比，计算结果如表4所示。其余未展示FIBFs与原始信号相关系数均小于0.02，能量占比均小于0.0005，可认为其为高频噪声分量。

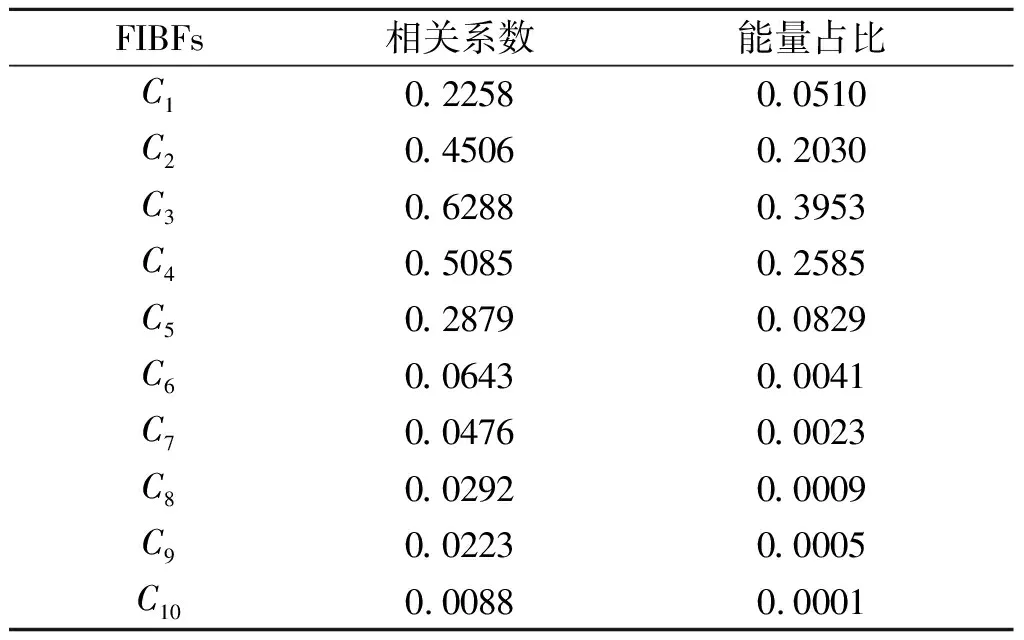
表 4 FIBFs与原始信号相关系数及其能量占比

由相关系数与能量占比可得，C1～C5与原始信号相关性较大，且占有原始信号大部分能量，可认为其为优势频带，构成主要的爆破振动效应危害，应对其进行重点分析。将其重构如图9所示。重构后信号在保留信号局部细节特征的同时，高频噪声分量被基本剔除。

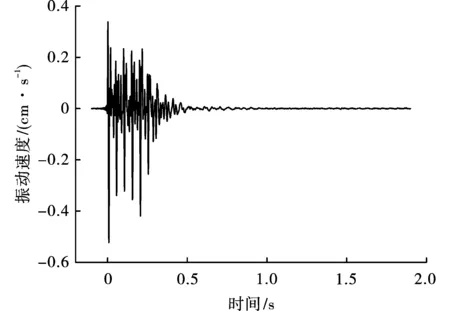
图 9 重构信号波形图Fig. 9 Waveform of the reconstruct signal

对C1～C5模态分量进行Hilbert变换，得到Hilbert谱，分析其时间-频率-能量之间关系。时频谱如图10所示。

由图10可以发现，基于FDM所得时频谱图在低频部分具有极高的分辨率，有利于精确提取爆破振动信号细节特征。观察时频谱图可发现，本工程爆破振动能量大部分位于0～50 Hz的低频段，主要集中于10～30 Hz左右。同时，可以发现，此爆破能量最大值出现在0.05 s时刻，为掏槽眼起爆时刻，说明掏槽眼爆破产生能量较大。为降低爆破危害，可采取降低掏槽眼药量、采用复式掏槽等合理的减震措施。

本工程为保护和平村房屋，根据《爆破安全规程》GB6722—2014[20]，属于保护对象为土窑洞、土坯房、毛石房屋的爆破工程。按爆破振动频率划分安全标准，当振动频率小于10 Hz时，安全允许振动速度为0.15～0.45 cm/s；当振动频率为10～50 Hz时，安全允许振动速度为0.45～0.9 cm/s；当振动频率大于50 Hz时，安全允许振动速度为0.9～1.5 cm/s。根据表3与图8，可得爆破振动速度满足规范要求，且爆破振动所对应的低频部分振速均较低。

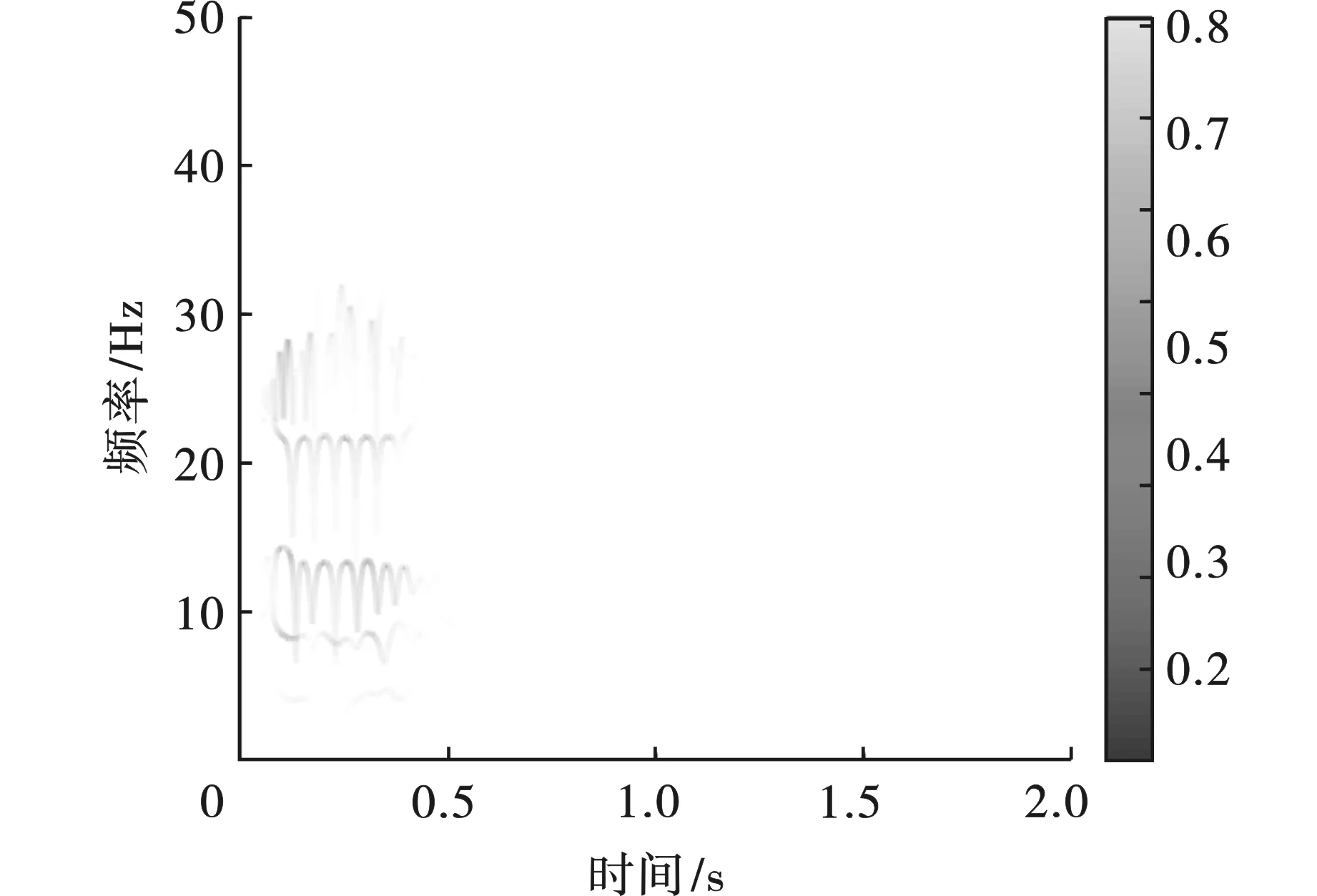
图 10 基于FDM的时频谱图Fig. 10 Time-frequency spectrum diagrams based on FDM

一般地面建(构)筑物的自振频率为10 Hz左右，故此爆破工程可能会引发村庄房屋发生共振而产生破坏，需通过合理得降震增频措施来减少爆破振动产生影响，如通过降低单段药量、增加雷管段位、优化装药结构等来降低爆破振动强度。

综上，基于FDM得隧道爆破振动信号时频分析方法，解决了传统方法模态混叠问题与噪声残留问题，且可以精确获取爆破振动信号细节特征，而由FDM分解所得FIBFs经Hilbert变换所得时频谱图在时域与频域上都有着良好的分辨率，有利于爆破振动信号分析与爆破振动危害控制。

4 结论

依托太锡铁路太崇段新建崇礼隧道下穿和平村实际工程，引入一种基于FDM的隧道爆破振动信号时频分析方法，得到如下结论：

FDM分解方法具有正交性、完备性、自适应性、局部性，无模态混叠现象与噪声残留问题。根据相关系数与能量占比选取FIBFs进行重构后可保留原始信号细节特征，且高频噪声被有效剔除，有利于进一步信号分析。

经FDM分解所得FIBFs经过筛选后进行Hilbert变换，所得时频谱在时域与频域均具有良好的分辨率，有利于对爆破振动信号细节特征进行精确分析。

基于实测信号的时频谱图分析可得，本工程爆破振速符合《爆破安全规程》GB6722—2014安全要求，爆破振动能量主要位于0～30 Hz的低频部分，应重点关注村庄房屋共振问题。