基于改进变分模态分解的电缆行波故障定位研究

吴学斌，黄治，邓惟绩

(1·国网湖南省电力有限公司，湖南 长沙410004；2·国网湖南省电力有限公司物资公司，湖南 长沙410004；3·长沙理工大学电气与信息工程学院，湖南 长沙410005)

0 引言

随着预制舱式智能变电站在电网的大力推广，对电缆的故障定位提出了更高要求[1－4]。目前电缆故障定位方法主要有单端测量定位法[5]和双端测量定位法。当电缆发生故障时，故障行波向两侧传播，由于线路阻抗及过渡电阻的存在，使检测到的故障行波信号具有突变性和奇异性，需对行波信号进一步分解变换，再进行时间准确标定[6]。

目前针对电缆行波故障定位方法已存在一些研究。其中文献[7]利用小波变换获得高频系数，利用模极大值法获取故障行波的模极大值序列，对初始波头到达时刻和反射波到达时刻进行标定，但由于去噪的需要，在每层小波分解时分解系数需要设置不同的阈值，较为复杂[8]。文献[9]利用小波包分解法提取能量谱特征量，代替直接提取固有频率，但该方法难以准确选定基函数和分解层数，误差较大。文献[10]利用经验模态分解法对故障行波进行经验模态分解，提取高频分量，并对其进行魏格纳威尔分布，通过瞬时能量峰值确定行波及反射波到达时刻，但该方法无法确定对原始信号的分解层数，以致出现过包络、欠包络和模态混叠等问题。

相较于经验模态分解法，变分模态分解法对含有奇异点的暂态故障行波信号具有良好的自适应性和去噪能力，可以进行分解尺度的预设。传统变分模态分解方法是通过不同分解尺度下分解出的各个分量中心频率之间的差值作为尺度分解预设的依据，需通过一定次数的预分解才能确定较好的分解尺度，否则影响分解效率。因此本文通过引入瞬时频率均值的概念，改进变分模态分解方法，通过观测瞬时频率均值进行预设尺度设置，然后进行魏格纳威尔分布，通过瞬时能量峰值来标定初始行波及第一次反射波到达时刻，对电缆行波进行故障定位。

1 电缆单端故障行波测距原理

电缆故障时，故障点会产生暂态行波，暂态行波产生后向故障点两端开始传播，因此可以通过测量暂态行波到达测量点时间和其反射波到达测量点时间，计算时间差来计算故障点位置。

如图1所示，电缆线路M1M2长度为l，F1、F2为故障点位置，故障点距M1端的距离记为X，M为线路M1M2的中点。

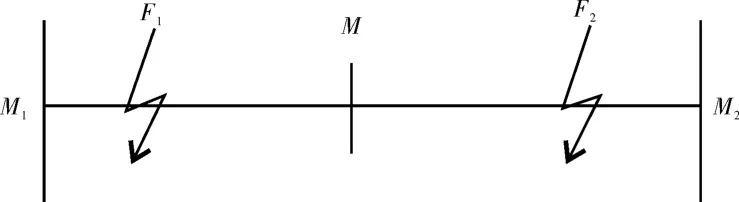
图1 电缆故障分布图

采用单端检测方法来进行故障定位，检测端位于M1端。当电缆发生故障时，故障点会产生突变信号，并向两侧传播，并伴随着多次的折反射现象。故障点位于M1M内时，行波分析如图2所示。

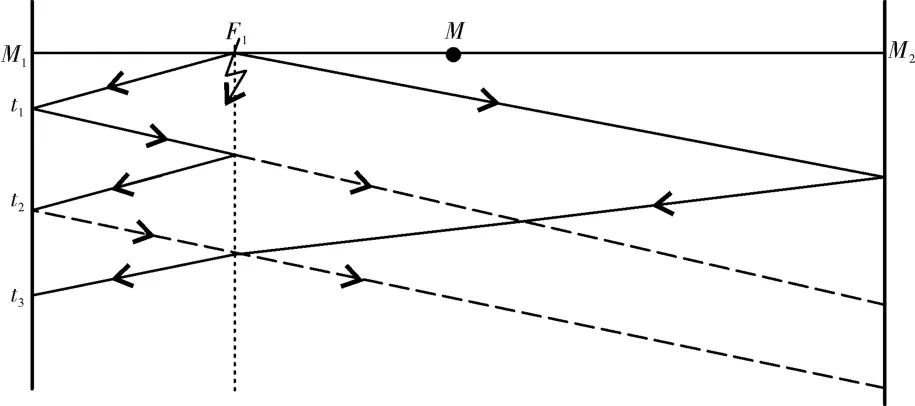
图2 前半段电缆故障行波分析图

单端故障定位法关键是对行波波头第一次到达检测端的时刻t1和行波经过故障点第一次反射波到达检测端的时刻t2进行标定，利用其时间差Δt＝t2－t1进行定位。行波的传播速度为:

式中，L为单位长度电感，C为单位长度电容。故障距离X1为:

当故障点位于线路后半段MM2时，电缆故障行波分析如图3所示。

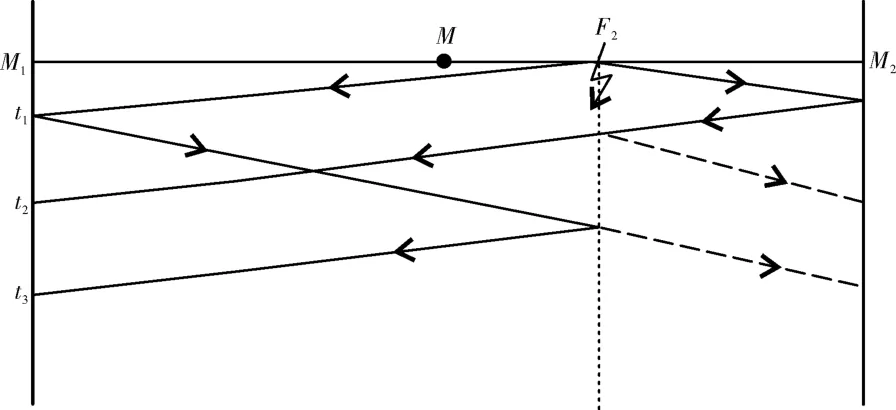
图3 后半段电缆故障时行波分析图

故障距离X2为:

根据分析可知，电缆故障能否准确定位主要取决于确定故障行波波头的准确到达时刻。

2 基于改进变分模态分解和魏格纳威尔分布的波头检测原理

2.1 改进变分模态分解算法原理

变分模态分解(VMD)是将一个输入的实际信号分解成一系列离散子信号uk之和，每一个子信号将会有一个中心频率ωk。为得出每种模式下的带宽，需要对子信号uk进行Hilbert变换得到单边谱，通过加入调制指数信号将该模式的频谱移到相应基带[12－13]，对变分模约束进行优化，如式(4)所示:

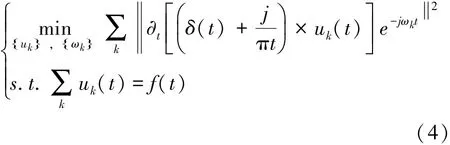
式中，uk为实信号分解所得到的K个模态分量，ωk为各模态分量的频率中心。

为求解式(4)约束问题，引入二次惩罚因子α和拉格朗日乘子λ，α的引入可以提高迭代收敛性，λ可以将变分模的最小值问题转换为求鞍点问题，引入后得到增广表达式如式(5)所示。

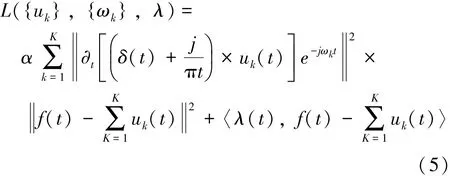
通过交替方向乘子法的迭代次优化序列得到各个模态分量及中心频率:

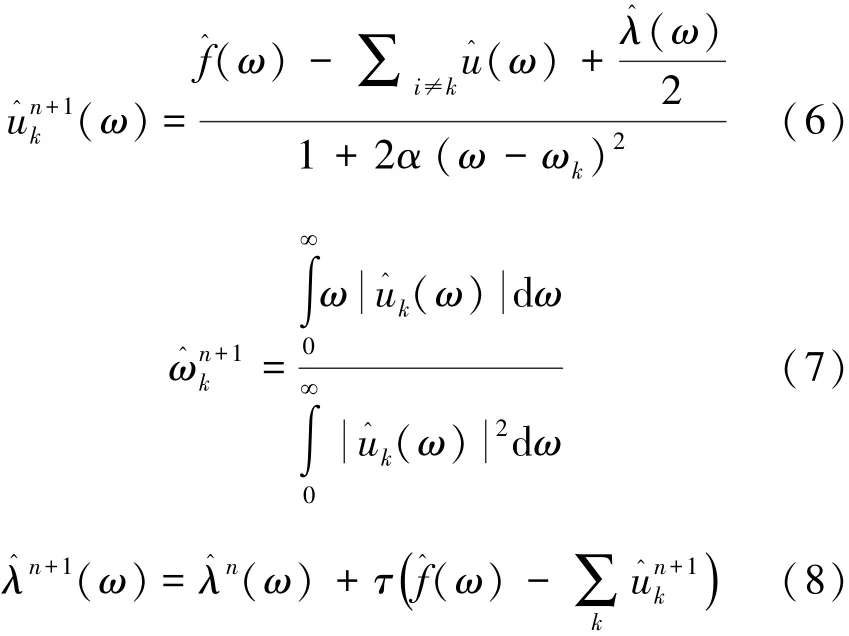
其算法流程如下:

2)迭代次数n＝n＋1。

3)Fork＝1:k，由式(6)进行模态更新为

4)Fork＝1:k，由式(7)进行ωk更新为

5)由式(8)进行λ更新。

2.2 VMD分解尺度优化

利用VMD算法进行模态信号分解时，若原信号可以明确由K个信号合成，则在选取K参数时较为直观，但电力系统发生电缆故障时，其行波信号往往难以确定模态函数的个数，因此对故障行波信号进行VMD分解前需先确定预设尺度K。预设尺度K的准确选择直接影响行波故障定位的准确性。

现有方法通常设定一个阈值，当两个中心频率之间的差值小于设定的阈值时则可确定预设尺度K[12]。但该方法需要经过多次的VMD分解确定K值，其运算收敛速度较慢，且阈值的设定随机性大，识别精度不高。为提高该方法的计算速度和故障定位精度，对此提出如下改进方法:

设连续时间信号x(t)，对x(t)进行Hilbert变换得到Y(t)，即:

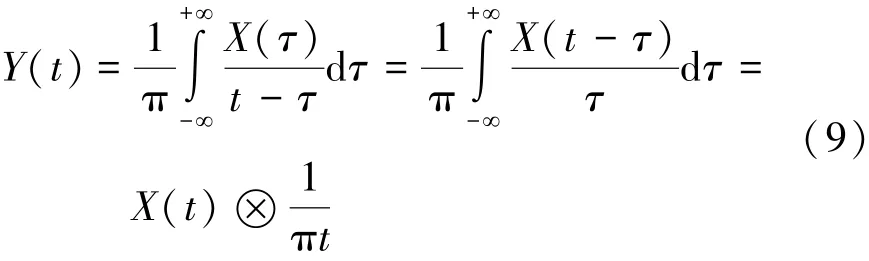
由x(t)和Y(t)得到解析信号Z(t)，即:

定义瞬时相位θ为:

信号的瞬时频率f(t)为:

在此定义分量瞬时频率的均值为μ，即:

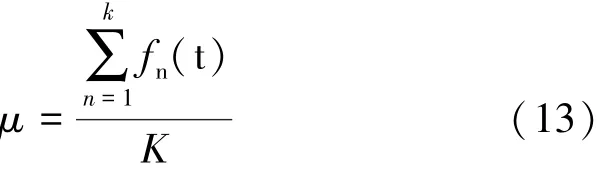
若对原信号分解个数过大，则分量会出现频率交叉混叠，瞬时频率的均值出现曲率较大的下折现象。通过分量瞬时频率的均值μ的变化情况对预设尺度K进行优化设置。

2.3 魏格纳威尔分布

魏格纳威尔分布(WVD)是一种双线性形式的时－频分布，反映了信号瞬时的时频关系，具有良好的能量聚集性同时还保持较好的分辨率，广泛应用于非平稳突变信号的时－频分析中[13－15]。因此可用于行波测距中波头到达时刻的标定。

设连续时间信号x(t)，对其进行傅里叶变换得X(jΩ)，x(t)的WVD为:

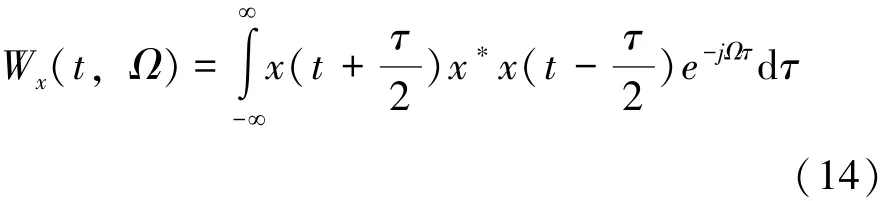
对式(14)两边同时对Ω进行积分:

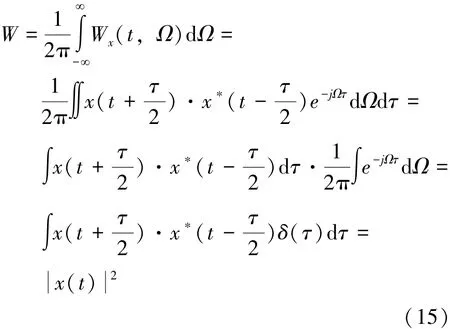
由式(15)可知，原始信号x(t)在t时刻的瞬时能量即为x(t)的WVD在频率轴的积分。

2.4 改进变分模态和维格威尔分布结合的波头检测方法

WVD在非平稳信号处理方面能够准确的表达信号随时－频变化，且同时保持着较高的分辨率。对故障信号进行WVD处理，观察故障信号随频率和时间的能量变化，找到瞬时能量的突变点，即可准确地标定波头到达时间。但故障信号往往存在较多交叉干扰项，需要用VMD对故障信号进行预处理。

主要步骤包括:

1)计算故障暂态信号的瞬时频率的均值，根据均值确定预设分解尺度。

2)根据预设分解尺度对故障暂态信号进行VMD，选取中心频率比较高的IMF分量作为故障暂态特征信号。

3)使用WVD求出该特征信号的瞬时能量，瞬时能量中尖峰对应的就是故障暂态初始波和一系列故障点反射波到达的时刻。

3 仿真分析

利用MATLAB搭建长沙某预制舱式变电站电缆输电线路模型，如图4所示。线路全长25 km，电压等级为10 kV，电缆型号为YJV32，设置电缆分布参数见表1。

图4 10 kV电缆输电线路模型

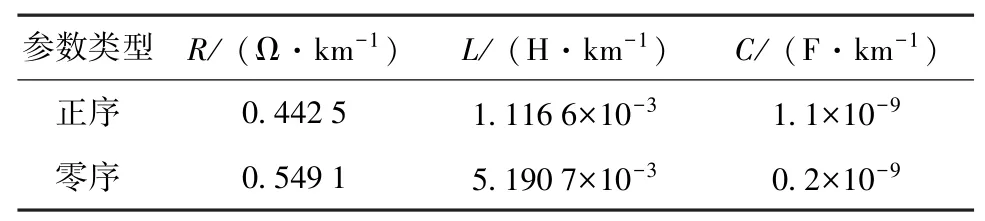
表1 电缆电气参数

在仿真模型中，设置采样频率为1 MHz，在距离A端5 km处设置A相接地短路，故障相相角设为30°，接地电阻设为10 Ω。对故障暂态电流信号进行变分模态分解，其在不同预设尺度下中心频率fk见表2。

表2 不同分解尺度下中心频率 Hz

从表2中可以看出，随着分解尺度的增加，相邻模态之间的中心频率的差值随之减小；当分解尺度K为4时，相邻两个模态之间的中心频率已经较为接近；当分解层数为5时，分解次数为15。

采用改进后的VMD分解算法，得到不同分解尺度下瞬时频率的均值变化情况如图5所示。

由图5不同分解尺度下的瞬时频率的均值分解情况可知，当分解尺度K≤4时，瞬时频率的均值μ缓缓下降；当分解尺度K≥5，瞬时频率的均值μ出现明显的曲率较大的下折现象，因此确定变分模分解的预设尺度为4，此时分解次数为5次，由此可以看出，改进后分解尺度设置方法的效率大大提高。

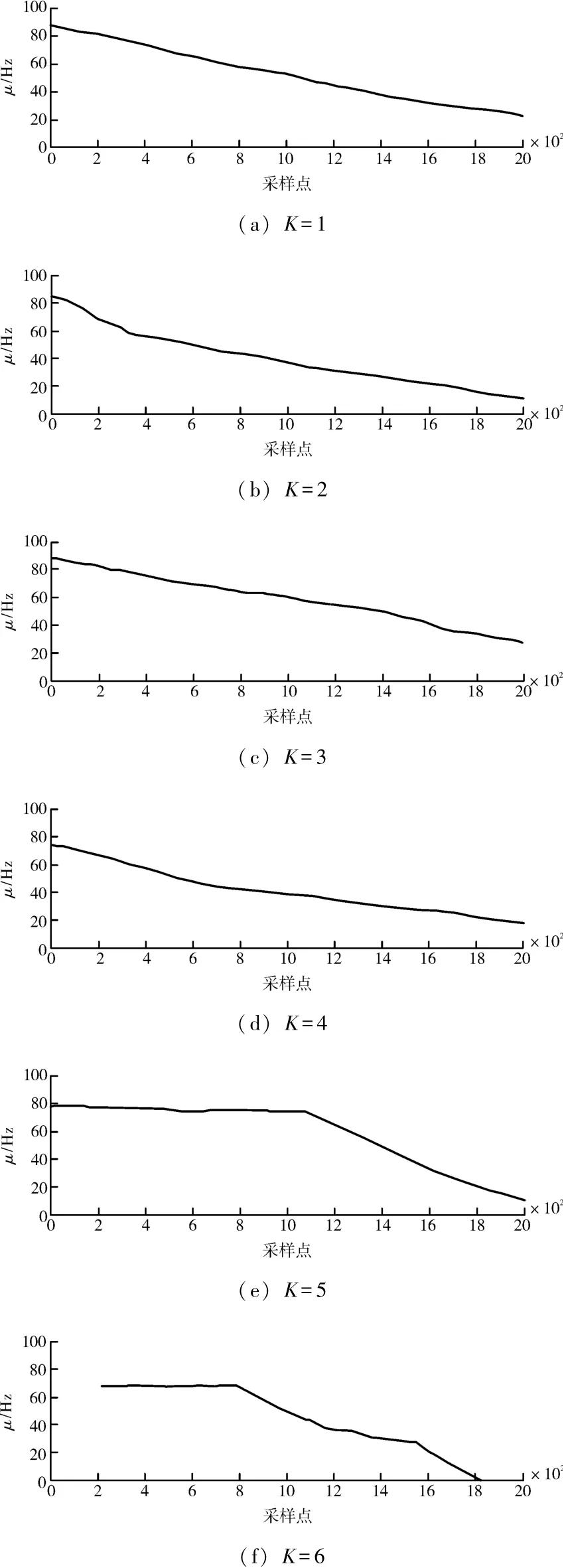
图5 不同分解尺度瞬时频率的均值变化

检测端A侧检测的故障电流局部波形如图6所示。

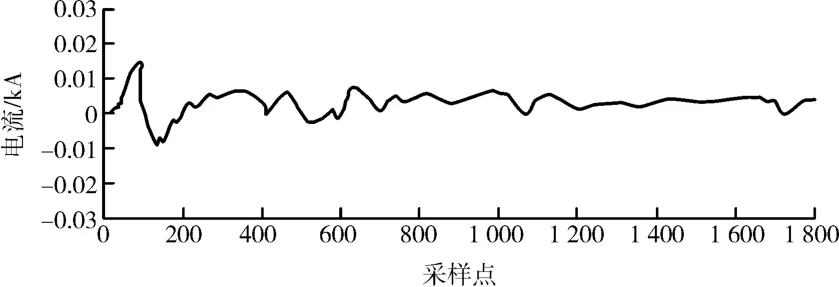
图6 检测端故障电路波形

图7分别为预设尺度K＝1、2、3、4时的VMD分解模态。

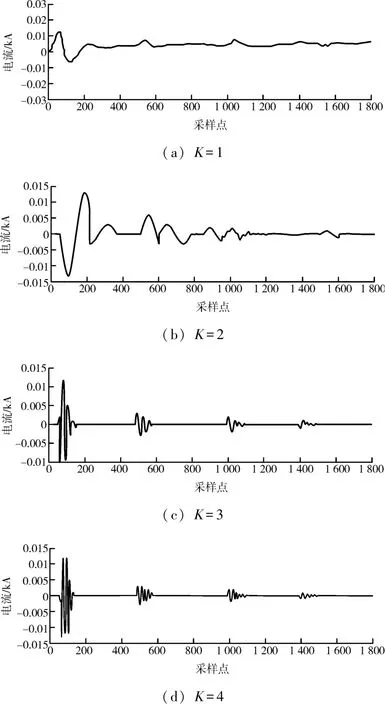
图7 VMD分解模态

由上可知在预设分解尺度为4，即K＝4时最为适合，再增大K值只会增加计算的难度，因此，选择对高阶本征模态4进行WVD分布，结果如图8所示。

图8 WVD分布后瞬时能量变化

当电缆输电线路发生故障时，行波瞬时能量快速达到最大值，并产生较大波动，由瞬时能量分布曲线可知，初始波头到达时刻的采样点为363，第一个反射波波头到达时刻的采样点为427。

在线路距离A端11 km、16 km处设置单相接地短路故障，其定位结果见表3。

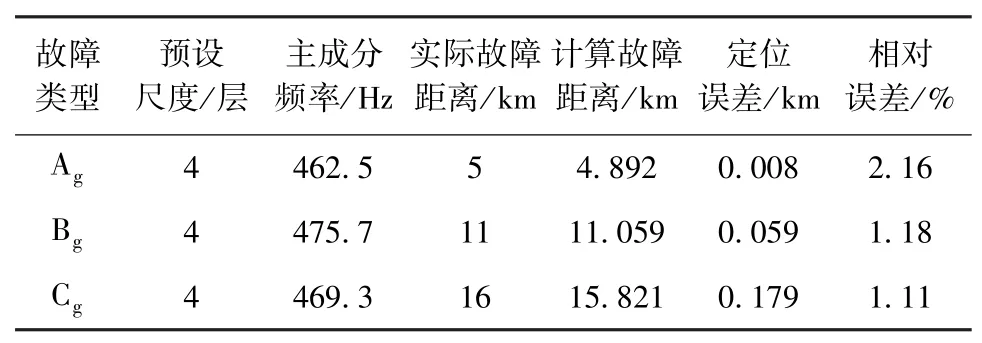
表3 不同故障距离测距结果

为验证不同故障类型对定位结果的影响，在距离检测端A侧8 km处设置短路相角为30°，接地电阻为15 Ω的不同故障类型，测距结果和测距误差见表4。

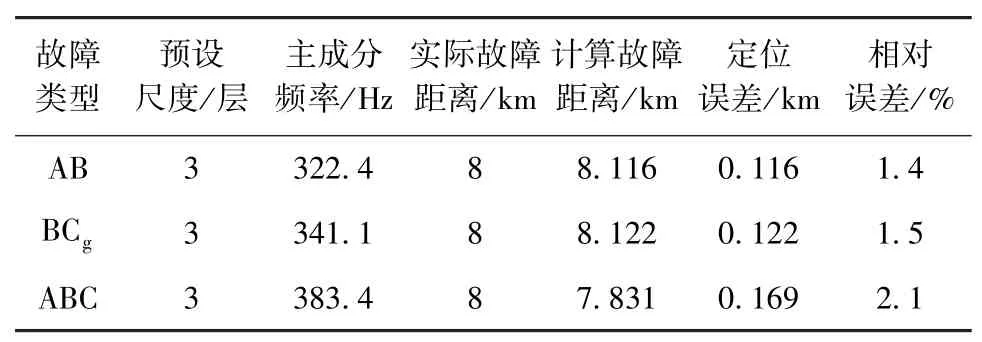
表4 不同故障类型测距结果

为验证不同接地电阻对定位结果的影响，在距离检测端A侧12 km处分别设置接地电阻为5 Ω、10 Ω、15 Ω，短路相角为60°的单相接地故障，测距结果和测距误差见表5。

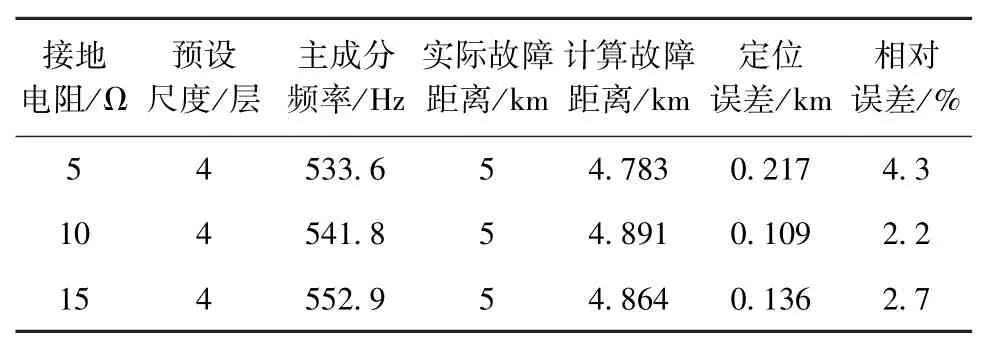
表5 不同接地电阻测距结果

在距离A侧13 km处设置AB两相短路故障，接地电阻为12 Ω，分别设置短路初始相角为30°、60°、90°，测距结果和测距误差见表6。

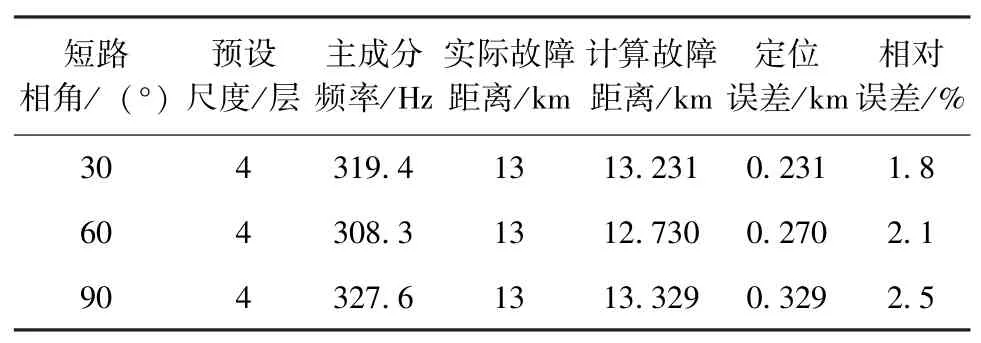
表6 不同短路相角定位结果

由表4—6可知，对于不同故障类型、接地电阻、短路相角最大测距结果其误差分别在170 m、220 m、330 m以内，相对误差较小，具有广泛的适用性。

4 结论

本文利用变分模态分解与魏格纳威尔分布相结合的方法对电缆行波进行故障定位。利用变分模态分解法将故障行波信号进行有效分离，相较于经验模态法，变分模态分解法通过分析瞬时频率的均值对变分模分解预设尺度进行优化，提高了分解效率。而魏格纳威尔分布能够准确的识别和标定初始波头和第一次反射波波头到达时刻。仿真结果表明，变分模态分解法能有效提高了分解效率，对于不同故障类型、接地电阻、短路相角时的故障定位，此外，本文方法相较于传统双段故障定位方法能够有效避免双端同步对时问题，减少成本，能够为提高电缆故障定位准确度提供参考，更好地应用于工程实践中。