基于粒度的加速求解约简策略

张昭琴,徐泰华,鞠恒荣,刘克宇,4,王平心

(江苏科技大学 1.计算机学院;2.理学院,江苏 镇江 212100;3.南通大学 信息科学技术学院,江苏 南通 226019;4.西南交通大学 计算机与人工智能学院,四川 成都 611756)

属性约简[1,2]是粗糙集[3,4]理论研究中的一项核心内容。作为一种有效的特征选择技术[5,6],近年来属性约简已然成为了众多学者关注的焦点,其主要思想是依据不确定性度量评估候选属性,筛选并移除部分属性,最终得到满足给定约束条件的最小属性子集。作为一种数据预处理技术,属性约简既可以对数据进行降维,从而降低后续学习任务的复杂性,又能在一定程度上提升学习器的泛化性能。

目前,大量学者除了根据实际应用需求,对属性约简的结构及形式进行广泛探索,还着眼于设计一些搜索算法,以期能够快速地得到有效的约简结果。一般来说,在兼顾考虑约简求解效率与约简结果有效性的同时,众多学者倾向于使用前向贪心搜索策略。然而需指出的是,该策略需依据给定的度量标准对所有候选属性进行逐一评估,直至满足算法终止条件。这一进程需要迭代地遍历所有的候选属性,才能得出最终的约简结果,因而在属性数量急剧增加的情况下,利用前向贪心搜索进行约简求解将显式地带来较大的时间消耗。

根据上述分析,利用前向贪心搜索求解约简时,时间效率依然可以进一步提升,例如采用一些选择性的策略[7],来达到减少候选属性数量的目的。鉴于此,本文在前向贪心搜索进程中,引入了粒度[8,9]的概念,用以度量各个候选属性对应的粒化[10]结果的粗细程度,使其能够在进行候选属性评估之前,剔除部分对应着较粗粒化结果的属性,从而减少需被评估的侯选属性的个数。这主要是因为考虑到如果某一属性对应着较粗的粒化结果,那么该属性对于降低粗糙集方法中的不确定性度量值的贡献度较弱,若将其加入到约简结果中,则对于约束条件的逼近作用不显著。利用这一选择性策略,通过比较不同属性上所对应的粒度的值,可以显式地减少每次迭代进程中候选属性的数量,从而达到压缩属性搜索空间,提升约简求解效率的目的。

1 基础知识

1.1 邻域粗糙集

(1)

式中:ΔA(xi,xj)表示依据条件属性集合A所求得的样本xi与xj间的距离,δ为给定的半径。

(2)

(3)

式中:Xp∈U/IND(d)。

1.2 粒度

以粒计算的视角来看,粒度这一概念常被用来表征信息粒化的程度。依据不同的信息粒化方式,粒度可以具有不同的语义解释[14]如下所示。

(1)基于属性的粒度。若利用基于属性集合的二元关系、聚类等方式进行信息粒化,则此时粒度就可以反映样本在这些属性上的区分程度。相应地,根据不同属性子集所具备的区分程度的差异,可以计算出不同的粒度值。

(2)基于参数的粒度。若利用基于参数的二元关系来进行信息粒化,则此时粒度就可以反映在该参数下样本的区分程度。类似地,使用不同的参数也可能得到不同的粒度值。

实际上,第1.1节所示的邻域关系本质上就是一种信息粒化的技术手段,这种邻域关系既体现了基于属性的粒度,也体现了基于参数的粒度。鉴于此,利用邻域关系,可以定义如下所示的粒度求解方法。

(4)

式中:|X|表示集合X的基数。

1.3 属性约简

属性约简[18]是一种有效的特征选择方法,依据不同的约简求解目标,已有学者提出了数十种属性约简的定义。然而,这些定义大都具有类似的结构,因此Yao等[19]总结了属性约简的一般表现形式,并给出的形式化定义如下。

(1)A满足约束条件Cρ,

其中ρ是一个函数,形如ρ:2U×2AT→R,R是所有实数的合集。

由定义4可知属性约简的一般表现形式,此时如何依据该定义求解约简就可被视作一个搜索问题。为此,学者们采用了诸多不同类型或结构的搜索算法,如完全搜索[20]、随机搜索[21]、贪心搜索[22]等。在这些策略中,前向贪心搜索因较低的时间复杂度,受到众多学者的青睐,此搜索策略的详细过程如算法1所示。

算法1前向贪心约简求解算法

输入:决策系统DS=〈U,AT∪{d}〉,约束条件Cρ;

输出:red;

步骤1 初始化,令red=∅;

步骤2 Whilered不满足约束条件Cρdo

(2)依据(1),找出当前迭代过程中一个合适的属性b∈AT-red;

(3)red=red∪{b};

End

步骤3 输出red。

在算法1迭代求解约简的过程中,最坏的情况下,条件属性集AT中的每个属性都需要被评估。因此,评估属性所需要的次数为(|AT|+1)·|AT|/2,此时该算法的时间复杂度为O(|U|2·(|AT|+1)·|AT|/2),即O(|U|2·|AT|2)。

2 基于粒度的约简加速求解算法

在粒计算领域中,粒度这一概念可以量化地描述属性所具备的分辨能力。一般来说,较细的粒度,即粒度值较小,表示属性具有较强的分辨能力,而较粗的粒度,即粒度值较大,表明属性具有较弱的分辨能力。

通过观察算法1,不难发现属性约简的过程实际上是与粒度的变化密切相关的,这主要是因为算法1是一个迭代地增加属性的过程,而随着属性不断地被评估并加入到约简池中,粒度将逐渐变细,即粒度的值将逐渐变小。由此可以得知:(1)在每次迭代过程中,所有候选池中的属性都需被评估;(2)候选池中的部分属性可能对应着较粗的粒度,这类属性往往具备较弱的区分能力,因而具有较粗粒度的候选属性可能会对属性评估以及计算约简的时间消耗产生不利影响。综合考虑以上两点,如何利用属性约简过程和粒度变化的关联,进一步提升评估属性及计算约简的效率,是一个突破口。

根据上述分析,在候选池中删除一些对应着较粗粒度的侯选属性,可以达到减少属性约简过程中侯选属性搜索范围的目的。因此,本文提出了一种基于粒度的加速求解约简策略,详细算法如算法2所示。

算法2基于粒度的加速求解约简算法

输入:决策系统DS=〈U,AT∪{d}〉,约束条件Cρ;

输出:red;

步骤1 初始化,令red=T=∅;

步骤4 根据步骤3,找到合适的属性b∈AT-red;

步骤5red=red∪{b};

步骤6 Whilered不满足约束条件Cρdo

(3)依据(2),找到合适的属性b∈T,red=

red∪{b};

End

步骤7 输出red。

相较于算法1,算法2在最坏情况下,评估属性所需的次数为(|AT|+1)·|AT|/2,则算法求解约简的时间复杂度为O(|U|2·(|AT|+1)·|AT|/2),即O(|U|2·|AT|2)。算法1和算法2两者就时间复杂度来看是一致的,但此仅局限于两种算法在最坏的情况下所得出的时间复杂度。大量前期测试结果表明,在求解属性约简的过程中,通过剔除部分对应着较粗粒化结果的属性,可以减少侯选属性的个数。这意味着可以减少评估属性所需要的次数,算法迭代次数会减少,进而可以达到快速约简求解的目的,具体的实验结果将在第3节中进行展示。

3 实验分析

为了验证所提算法的有效性,本文从UCI数据集中选取了12组数据集,数据集的基本描述如表1所示。实验均采用MATLAB R2018a实现,操作系统为Windows 10,CPU为Intel®Core(TM)i5-4210U,内存为8.00 GB。

表1 数据集描述

本节实验分别采用了3种不确定性度量准则,来构造定义4中所示的约束Cρ,从而实现算法1和算法2,这3种不确定性度量分别是近似质量[23]、条件熵[24,25]和邻域鉴别指数[26]。此外,因为本文采用的是邻域粗糙集作为模型,因此,对于每一组实验,都分别选取了0.01、0.02、…、0.20等20个半径[27],并利用交叉验证[28]的方法进行约简求解。

3.1 时间消耗比对

图1展示了利用两种算法和3种不确定性度量,在12个数据集上计算约简的时间消耗。

图1 求解约简的时间消耗

由图1,可得出如下结论:

(1)无论采用哪一种不确定性度量,相较于算法1,所提出的算法2确实可以对约简的求解过程进行加速,从而使得时间消耗显著降低。以数据集“Australian sign language signs”为例,若采用近似质量度量构造约束,算法1在半径设置为0.08时,求解约简需耗时16.135 8 s,而算法2仅需耗时9.839 3 s;若以邻域鉴别指数为度量标准构造约束,算法1在半径设置为0.12时求解约简需耗时2.788 8 s,而算法2仅需耗时2.308 3 s。由此可见,相较于传统前向贪心约简求解算法,基于粒度的加速求解约简算法在获取约简的效率上具有显著优势,这与算法的设计初衷是保持一致的。在每一轮迭代选择属性的过程中,剔除了一些对应着较粗粒化结果的属性,减少了侯选属性的个数,从而使得评估属性时计算次数减少。

(2)本文提出的算法在不同类型的样本数据集上,都体现出了较好的加速效果。以数据集“LSVT voice rehabilitation”和“Cardiotocography”为例,前者样本数是126,属性个数为256;后者样本数是2 126,属性数目为21。从求解约简所需时间消耗的角度来看,在利用近似质量为度量来构造约束的情形下,前者在算法1且半径为0.09的情况下求解约简需耗时3.108 7 s,而算法2仅需耗时1.692 3 s;后者在算法1且半径设置为0.09的情况下求解约简需耗时71.121 7 s,而算法2仅需耗时43.466 3 s。由此可见,尽管两组数据就样本和属性的比例来看,存在显著的差异,但是从求解约简所需时间消耗的角度来看,本文提出的算法在这两组数据上都表现出了良好的性能。

3.2 分类准确率对比

在本组实验中,采用了常用的K最近邻分类器(K-nearest neighbor,KNN,K=3)和支持向量机[29](Support vector machine,SVM,libSVM默认参数)两种分类器分别对所求得的约简的分类性能进行测试。因为在求解约简时采用了五折交叉验证,因此在每一轮使用四折样本求得约简结果后,都可以使用剩下的那一折样本进行分类测试,最终求得平均分类准确率。其详细结果分别如表2和表3所示。

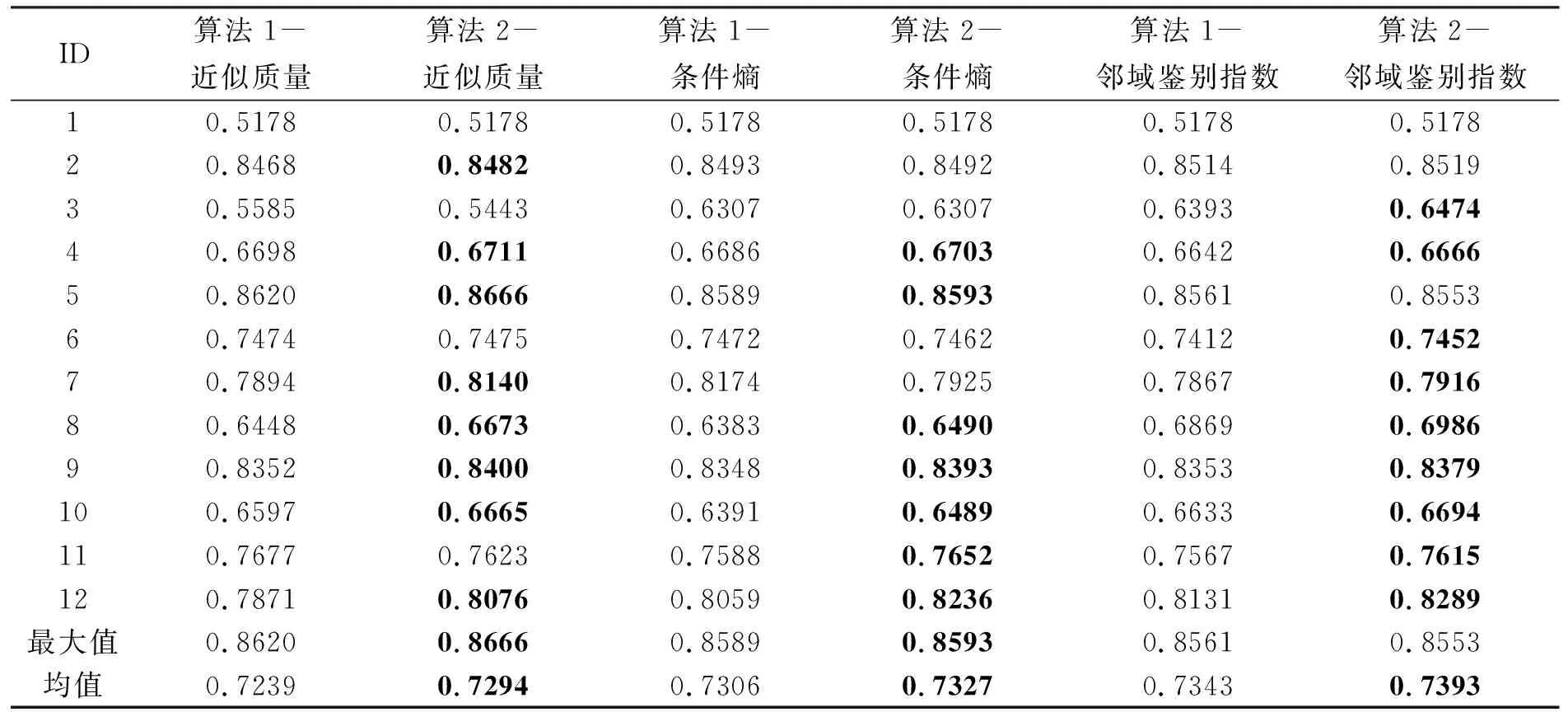
表3 SVM分类器的分类准确率

通过对比表2和表3展示的结果,不难发现,本文所提出的算法2在大多数情况下都能得到令人满意的分类准确率。举例来说,在表2中,以数据集“QSAR biodegradation”为例,采用3种不同的不确定性度量分别构造约束,算法1求得的约简结果所对应的分类准确率分别为0.841 7、0.840 4和0.841 5,而算法2求得的约简结果所对应的分类准确率分别为0.842 6、0.841 3和0.843 2;在表3中,以数据集“Waveform database generator”为例,采用3种不同的不确定性度量分别构造约束,算法1求得的约简结果所对应的分类准确率分别为0.787 1、0.805 9和0.813 1,而算法2求得的约简结果所对应的分类准确率分别为0.807 6、0.823 6和0.828 9。由此可见,相较于传统的前向贪心策略所求得的约简,基于粒度的加速求解约简策略能够使得所求约简具备相似的分类能力。

综合3.1节和3.2节所述内容,不难发现,相较于算法1而言,算法2可以在保证缩短求解约简时间消耗的同时,提供满意的分类准确率。

4 结束语

考虑到基于前向贪心搜索策略求解约简时,需评估所有的候选属性,导致时间消耗过多的问题。本文依据属性约简过程和粒度变化的关联,提出了一种基于粒度的加速求解约简策略。该策略通过在属性约简进程中,剔除对应着较粗粒度的属性,压缩候选属性的搜索空间,进行快速约简求取。实验结果表明所提出的算法在多种度量下,能够有效地降低求解约简所需的时间消耗,同时也保证了所求得的约简具备令人满意的泛化能力。

在此基础上,今后将进一步探讨如下问题。

(1)所提算法是一个框架性的结构,文中只使用了邻域粗糙集及相关度量进行讨论,也可以采用其他诸如不具备单调性的粗糙集模型和度量进行算法的进一步提升。

(2)将约简结果的稳定性纳入讨论范围,可以进一步考虑如何在提升约简稳定性的同时,确保求解约简的效率。

(3)本文所提算法是基于粒度的角度,在属性选择的过程中压缩候选属性的搜索空间。为了进一步提升算法的性能,可以考虑增加样本层面的加速策略,与基于样例选取的属性约简算法[30]进行结合,以期更进一步地提升约简求解的效率。