基于散乱点云的三维服装建模

王巧丽， 徐増波， 杨思

(上海工程技术大学 纺织服装学院，上海 201620)

三维虚拟试衣使消费者能够提前感知服装穿在身上的实际效果，该技术的应用可提高消费者的购物效率，有利于消费者购买到适合自己体型的服装，从而提高消费者满意度[1]。然而，在服装网络销售系统中，服装展示多是二维图片的形式，并不能全面展示服装各角度的信息，且三维服装建模的复杂性导致服装模型数据量少。因此，需要一种可以快速构建三维服装模型的方法来解决这一系列问题。

目前，三维服装建模技术主要分为服装物理建模、几何建模和混合建模。服装物理建模的基本方法是通过服装衣片建模、虚拟缝合技术和碰撞检测技术[2]对衣片模型进行构建与缝合，形成三维服装模型[3]。这种方法构建的服装模型通常款式比较简单，视觉效果不够真实。服装几何建模是通过三维模型表面各种几何拓扑结构的变化生成服装模型，常见的有4种类型：参数化曲面建模、二维手绘草图建模、基于现有模型生成新模型、基于三维扫描的服装建模。服装混合建模结合了物理建模和几何建模的优点，计算时间短、仿真效果好，但算法复杂，有待改善。

在服装物理建模方面，方贵盛[4]发现一种以草绘图为基础的衣片构建方法，该方法主要针对衣片轮廓线进行处理，实现衣片的交互式设计，从而丰富服装模型的款式。UMETANI N等[5]开发了服装交互式建模与编辑的服装设计工具，得到虚拟缝合后服装模型的特殊效果，更直观地呈现服装的三维效果。孟田翠[6]建立了一个虚拟试衣服装布料仿真系统，可利用人体包围盒将三维布料转换为多种款式的服装，且能对服装的褶皱和悬垂特性进行仿真。在几何建模方面，BROUET R等[7]通过对衣片顶点的调节实现服装模型各部位的形变，但这需要对大量顶点信息进行储存与计算，因此效率很低。颜家峰[8]提出一种基于样式维持的服装生成算法，通过已有的服装样式生成基本维持原有样式且适合人体模型的三维服装模型。在混合建模方面，WANG C等[9]通过计算服装张力在人体上的分布情况，控制缝合时模型在张力下的变形效果，提高服装模型的仿真效果。OSHITA M等[10]使用几何建模在稀疏粒子上生成褶皱细节，并使用文献[11]提出的PN三角化生成平滑的类织物曲面，但生成的褶皱会受给定图片的影响，织物的仿真效果还有很大提升空间。

目前，三维服装建模方法普遍较复杂，由于服装款式繁多且更替速度较快，为快速构建三维服装模型，文中提出一种优化用户体验的服装建模方法，强调操作简便，不需要过多的专业知识及操作过程便能完成服装建模。

1 服装点云数据的获取

1.1 服装点云采集

上海工程技术大学与东方国际集团有限公司联合研发的服装智能定制3D测体仪如图1所示。该设备基于Kinect摄像技术捕获目标的点云数据，生成三维人体点云模型。

图1 服装智能定制3D测体仪Fig.1 3D measuring instrument of clothing intelligent customization

1.2 服装区域点云提取及散乱点云拓扑关系的建立

基于点云重建的服装建模方式属于几何建模的范畴，为了使服装模型在虚拟试穿后具有自然褶皱等穿着真实感，需要将服装点云从人体上分割提取出来。在对散乱点云进行分割前，需要建立数据之间的拓扑关系，以便快速获取领域信息。文中利用KD树对点云数据构建拓扑结构。KD树是一种可以在K维空间划分数据点的二叉树结构，其基本原理是不断地用垂直于坐标轴的超平面将K维空间进行划分，从而形成一系列K维超矩形区域[12]。三维空间中，KD树空间划分示意如图2所示。

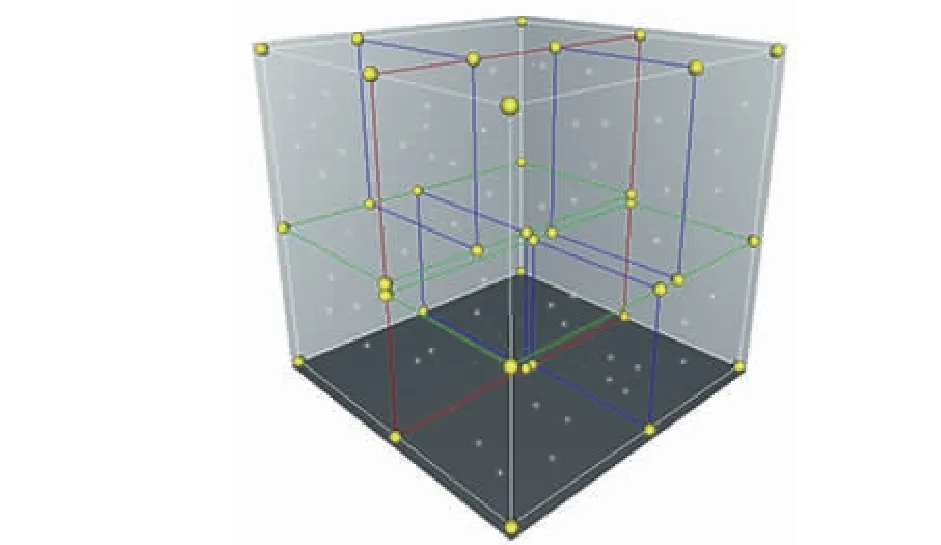
图2 KD树空间划分示意Fig.2 KD tree space division diagram

由于原始点云中上身服装区域与人体有明显的颜色区别，为了从人体与服装的整体中提取服装点云数据，采用基于颜色的区域增长算法进行分割。服装区域点云分割前后效果对比如图3所示。图3(a)为采用服装智能定制3D测体仪采集的服装点云数据，图3(b)是经过基于颜色的区域增长算法得到的服装区域点云。

2 服装点云数据的预处理

由三维扫描仪获取的点云数据在网格重建前通常需要预处理，以优化重建网格模型的质量。针对原始点云数据存在的离群点、冗余点、混杂点等现象，分别进行点云去噪、点云精简和点云平滑处理。

2.1 点云去噪

使用常见的3种点云去噪算法(统计滤波、半径滤波、直通滤波)对服装点云数据进行去噪，去噪效果分别见图4、图5和图6。去噪后的点云数量及算法运行时间见表1。

图3 服装区域点云分割前后效果对比Fig.3 Effect comparison before and after point cloud segmentation in clothing area

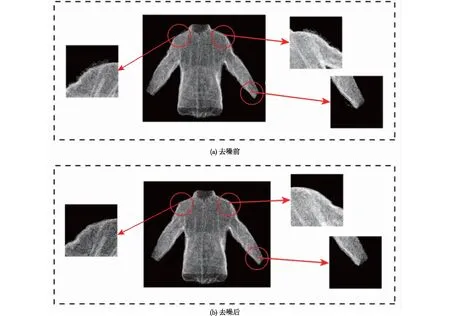
图4 统计滤波去噪前后效果对比Fig.4 Effect comparison before and after statistical outlier removal

图 5 半径滤波去噪前后效果对比Fig.5 Effect comparison before and after radius outlier removal

原始点云在肩部、袖口、背部等轮廓边缘有大量离散点，因此主要比较这些部位的去噪效果。由图4～图6以及表1可以看出，统计滤波去噪效果良好，运算速度较快；半径滤波运行速度快，但圆的半径和圆内点的数目需要人工指定，不够便捷；直通滤波基本没有去噪效果，且滤波范围的划分要求严格。因此，本文选择统计滤波作为离散点的去噪算法。

2.2 点云精简

点云滤波后服装边缘仍存在少量离散点，需要进行点云精简去除。随机下采样、平均网格法、非均匀网格采样法计算简单，且能使点云密度更加均匀，因此本文对比这3种算法的点云精简效果。采用随机下采样对服装点云进行精简时，percentage参数为需要精简的点云数占比，分别取0.1，0.3和0.5；采用平均网格法对服装点云进行精简时，gridStep参数为指定3D选框的大小，分别取0.10，0.15和0.20；通过非均匀网格采样法对服装点云进行精简时，maxNumPoints参数为网格框中的最大点数，分别取6，12和18。点云精简后的效果见图7，精简后点云的数量见表2。

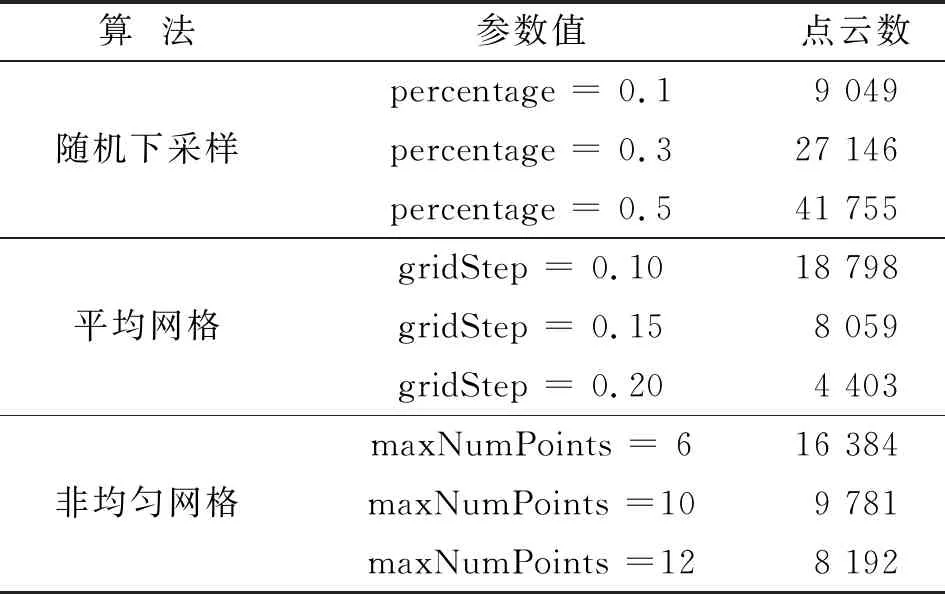
表2 点云数量对比

点云精简程度越大，留下的细节特征越少，因此需要在去除大量冗余点的同时，保留能够反映模型特征的数据点。对比各算法取不同参数时的点云精简结果，随机下采样在参数取0.3、平均网格参数取0.10与非均匀网格参数取6时的细节特征不相上下，但随机下采样法与平均网格法比非均匀网格法的点云分布更规则，更适合对称性的服装；再对比点云数量，平均网格比随机下采样少了近三分之一，因此选择平均网格参数为0.10时的精简结果供后续处理。

2.3 点云平滑

为了建立光滑完整的模型必须对服装表面进行平滑处理和孔洞修复，采用移动最小二乘法可以实现点云平滑。移动最小二乘法在拟合函数的建立中用系数向量和基函数代替了传统的多项式或其他函数，能够缓解或解决传统曲线曲面在拟合过程中存在的困难；在影响区域定义权函数，不同的权函数可以改变拟合曲面的光滑度。点云平滑后的服装表面见图8。

图8 点云平滑Fig.8 Point cloud smoothing

3 三维服装建模

结合区域生长算法和Delaunay三角剖分算法，以无向点云为输入，通过三角剖分形式生成插值曲面的算法进行服装模型重建。以点云重建的Delaunay四面体作为输入点种子三角形的开始，将与初始前沿边连接的Delaunay三角形逐个相加，逐步形成曲面。在曲面生长过程中，通过改变三角形的选择准则和调整三角形的添加顺序，可以减少由于添加不合适的三角形而产生的拓扑误差和孔洞数量。具体步骤如下：

Step 1 通过对服装散乱点云进行Delaunay三角剖分[13]得到三角形集TZ；

Step 2 在输入点的良好采样区域选择种子三角形作为初始曲面区域，种子三角形的3条边构成网格生长区域的初始前沿边(位于三角形区域与四边形区域分界线上的边。)；

Step 3 对每个前沿边执行迭代三角形加法策略，用于网格增长；

Step 4 当曲面上没有前沿边或前沿边都找不到适合生长的候选三角形时，算法停止。

3.1 种子三角形的选取

种子三角形的选择是区域生长方法中的一个重要步骤，正确地选取种子三角形是高质量曲面重建的前提。找到正确的种子三角形的关键是确保选定的三角形是曲面三角形。文中提出了一种高精度、低复杂度的种子三角形选择策略。图9为种子三角形的选取示意，具体步骤如下：

Step 1 从输入的散乱点云集中随机选择一个点v，然后从集合TZ中找到与v点相连的最小外接圆的三角形，假设找到的三角形是t。

Step 2 设t的三条边分别为e1，e2和e3，从TZ中找出与e1，e2和e3相连的外接圆最小的3个三角形，分别称为t1，t2和t3。如果t和t1，t2，t3之间的最大角度θ小于θseed(θseed的建议值为20°)，则进入Step 3；否则，选择另一个点作为v并重新进入Step 1。

Step 3 为了确保三角形位于曲面上，需要验证穿过三角形顶点且其轴平行于三角形法线的圆柱体在三角形外侧为空，换言之，此圆柱体中包含的点必须全部位于三角形上方或下方，则种子三角形选择完成[14]；否则，选择另一个点作为v并返回Step 1。

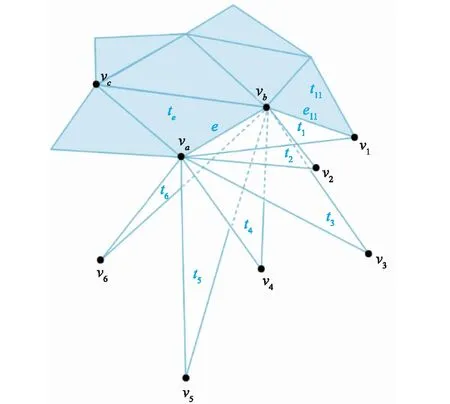
图9 种子三角形的选取Fig.9 Candidate triangle selection

3.2 候选三角形的选取

对于每个前沿边，需要从集合TZ中选择候选三角形，以满足当前网格的增长。曲面重建的结果受所选三角形的影响很大。为了使重构后的曲面与尽可能多的非噪声输入点相连接，减少生成曲面上的孔洞，候选三角形的选取应满足曲面拓扑条件、相邻三角形的角度条件和三角形不相交条件。图9中，令曲面三角形的集合为TS，前沿边的集合为Ef。对于任意e∈Ef，假设TZ中有m个三角形与e相连。在这些三角形中，只有一个三角形te∈TS，除te外，集合TE包含m-1个三角形，TE={t1,t2,…，tn,…,tm-1|tn≠te,1≤n≤m-1}。对于任意三角形tn，tn在e上的两个顶点是va和vb，另一个顶点称为vn。除e外，tn的边称为e1n和e2n。

3.2.1曲面拓扑条件 ①三角形tn的顶点vn不是内点；②三角形tn的三条边(e，e1n，e2n)都不是内边。

3.2.2相邻三角形的角度条件tn与te之间的夹角应小于常数值θsliver(θsliver的建议值为150°)。

3.2.3三角形不相交条件 对于三角形tn，若能找到除tn以外与e相连的三角形tn′∈TE，同时满足以下3个条件：①tn′的顶点vn′不是内点；②过点vn′向tn引垂线，与tn平面交于点vh，则三角形相交，若使tn添加至网格会导致其他一些点无法连接到网格。

3.3 网格生成

通过控制网格生长数量，可以看到服装点云网格化的过程，如图10所示，图中绿色边线的三角形为种子三角形，由种子三角形的3条前沿边开始，向外蔓延添加候选三角形，再从候选三角形的前沿边继续添加候选三角形。

图10 服装点云网格化过程Fig.10 Clothing point cloud gridding process

3.4 服装模型重建结果

使用泊松法和贪婪投影三角化法以及文中算法对同一服装点云数据进行重建，以三视图形式展示其效果，具体如图11所示。

图11 曲面重建结果ⅠFig.11 Surface reconstruction results Ⅰ

图11(a)中，贪婪投影三角化重建能够很好地还原点云原有的形状，应有的开口孔洞也得到了很好的保留，但由面片图可以发现，贪婪投影三角化重建的服装模型表面的三角面片起伏不平，衣片不够平滑。图11(b)中泊松法重建的网格均匀质量较好，面片显示效果相对平整，衣服原有的褶皱也得到了保留。但由俯视图可以看出，泊松重建对原本应保留的领部开口的孔洞进行了自动填补，底部下摆开口和袖口也是同样的问题；在边界进行补点和过度平滑，如在衣袖与衣身之间进行了补点，使衣袖与衣身出现连结现象；衣袖内部的干扰点也进行了过度重建，使衣袖上出现孔洞现象。图11(c)中所使用的重建方法，同时具备泊松法和贪婪投影三角法的优点，得到的34 960个三角形网格分布均匀、基本无错乱，面片光滑，同时保留了服装点云原有的形状，服装点云原有的开口也很好地予以保留。

为验证算法的普适性，对另外两组不同款式的服装点云数据进行了同样的重建结果对比，具体如图12所示。3种算法重建结果的特征与上文分析的类似，表明文中算法有更好的重建效果。

图12 曲面重建结果ⅡFig.12 Surface reconstruction results Ⅱ

4 结语

文中通过对实体服装进行点云的采集及预处理，对服装点云进行曲面重建实现了三维服装建模，并将该法与贪婪投影三角化重建、泊松重建进行了对比。结果显示：文中算法重建效果更好，服装网格分布均匀，面片光滑，且保留了服装原有的形状。该算法在尽可能保证服装还原度与运算速度的基础上，强调操作简便，不需要过多专业知识及操作过程便能完成服装建模。