考虑风能不确定性的压缩空气储能容量配置及经济性评估

虞启辉 ，田利 ，李晓飞 ，李晓东 ，谭心 ，张业明

（1内蒙古科技大学，内蒙古 包头 014010；2流体动力与机电系统国家重点实验室，浙江 杭州 310027；3气动热力储能与供能技术北京市重点实验室，北京 100191；4河南理工大学机械与动力工程学院，河南 焦作 454000）

随着环境污染问题的日益突出，风能等清洁的可再生能源将发挥更重要的作用，但是风力发电的高可变性和不确定性问题给风能的广泛应用带来了重大挑战[1]。储能系统(ESS)可以在非高峰时间存储多余的能量，并在能量不足的时间释放多余的能量，克服了风能的常规性和季节性波动[2]，成为了维持能量转换之间平衡的一种重要方法。与其他储能技术相比，CAES具有存储时间长[3]、成本低和响应时间快等优点，更加适用于风力发电场储能配置。

目前，国内外就CAES系统参与风电场储能配置领域，取得了许多成果。如孙浩等[4]通过实验平台验证了大型风电场耦合CAES系统在技术领域的可行性。文献[5]面向风电耦合传统CAES系统，提出了一种日前调度策略，该策略以提升联合系统运行收益为目标。文献[6]则针对太阳能和风能发电厂，提出了配置CAES系统的设计方法，并计算了CAES系统的整体性能，但是其不足之处是没有考虑风力发电和负荷需求的不确定性。吴晨曦等[7]考虑市场元素，建立了以断电赔偿和投资成本最小为目标的评估模型，并采用动态规划法优化了AA-CAES存储规模，获得最小成本为17950万元，不足之处是没有考虑用户负荷需求的变化。Jabari等[8]建立了耦合CAES微型能源系统，并采用混合整数非线性规划对每个组件进行了优化，降低了能源投资成本。Yan等[9]在CAES储气罐等约束条件下，建立了以系统的成本和排放量最小为目标的多目标优化模型，并通过改进的NSGA-II优化算法获得了系统最佳存储规模和运行参数。

在此背景下，本文针对间歇性风电场中CAES储能配置这一研究方向，提出了一种考虑风力和负荷需求不确定性的CAES系统规模优化配置方法，并以系统最大效益为目标分析了CAES系统在不同运行模式下的经济性。

1 风电耦合CAES系统建模

风电耦合CAES系统的设计方案的系统结构如图1所示，该系统由风电场、电网、压缩空气储能系统(CAES)和用户负荷需求中心组成。CAES工厂可以克服风电的随机特性缓解供需矛盾，同时电力短缺时可以通过接入当地电网来补充，以下对各单元分别进行了描述。

图1 风电耦合CAES系结构图Fig.1 Structure diagram of wind power coupled CAES system

1.1 模拟风电场和用户需求不确定性模型

风力多变性和不可预测性是风能资源应用面临的两大挑战[10]，使用平衡输出功率的CAES等设备与优化策略相结合的方法应对第一个挑战，是非常有效的。另一方面，克服第二个挑战需要结合用户需求对确定性策略进行一些修改。

1.1.1 每小时风力和Weibull分布

为了分析每小时风力输出，本研究采集了2019年夏县2个月间的风电场实时风速，如图2所示。显然，风力输出是不确定的，为了建立确定性风力输出模型，区别于使用具有加权因子的5个代表日[11]，或采用高斯法[12]拟合风力发电数据构建随机模型。本文使用广泛应用于处理不确定性风力问题的威布尔(Weibull)概率分布函数[10]进行建模，其数学表达式见式(1)

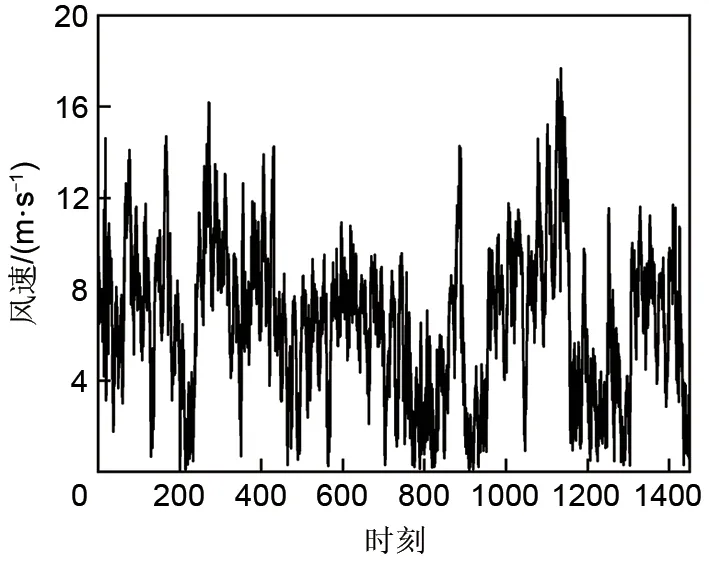
图2 风电场实时风速Fig.2 Real-time wind speed of wind farm

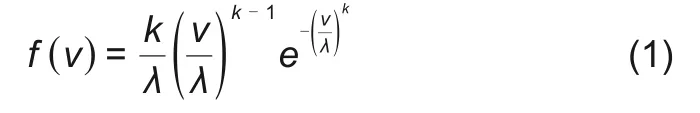
式中，f(v)为概率密度函数；k为形状参数；λ为尺度参数。

风电场使用的设备为FD70b风力涡轮机，其参数见表1。建模方法如下，以第1小时为例，首先依照标准IEC61400—12—1[13]，将每天0:00—1:00时处于切入切出风速间的有效风力数据进行汇总；然后，采取风速区间法[14](Bin法)以0.5 m/s的整倍数为中心划分区间并逐区计算其概率密度；最后，汇总上述数据估计概率曲线的参数，进而建立威布尔分布曲线。图3为0:00—1:00时风力分布概率图，在该时段λ=9.5066、k=3.7573的威布尔分布可以很好地拟合风力的变化，初步验证了Weibull分布建模的可靠性。因此，要基于威布尔概率分布构建有代表性的小时风力输出功率曲线，主要步骤如下。

表1 FD70b参数表Table 1 FD70b parameter table

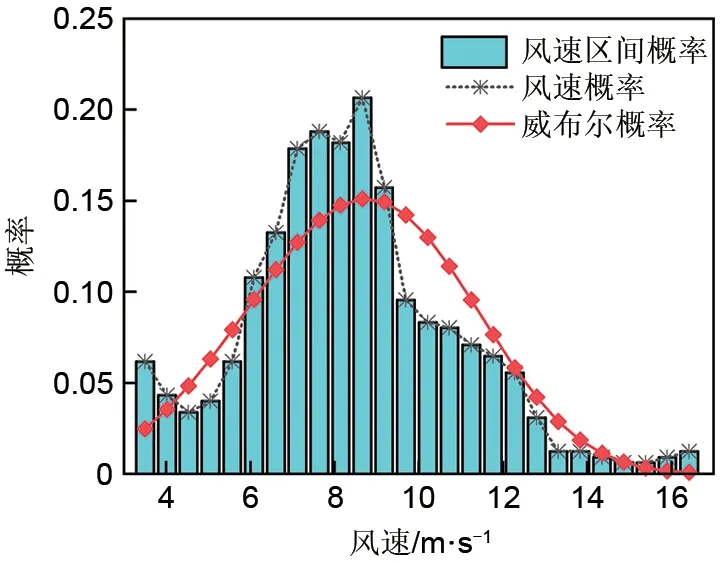
图3 0:00—1:00风力分布概率图Fig.3 0:00—1:00 Wind distribution probability graph

（1）根据Weibull分布概率密度函数求解其每小时区间概率分布。

（2）通过加权平均法获得每小时的期望功率，等式描述见式(2)

式中，PW(t)为t时刻风机输出功率；f(t,PWi)为t时刻功率值等于PWi的概率。

（3）按照上述步骤执行，可获得典型小时功率曲线，见图4，其每小时平均输出功率791 kW。

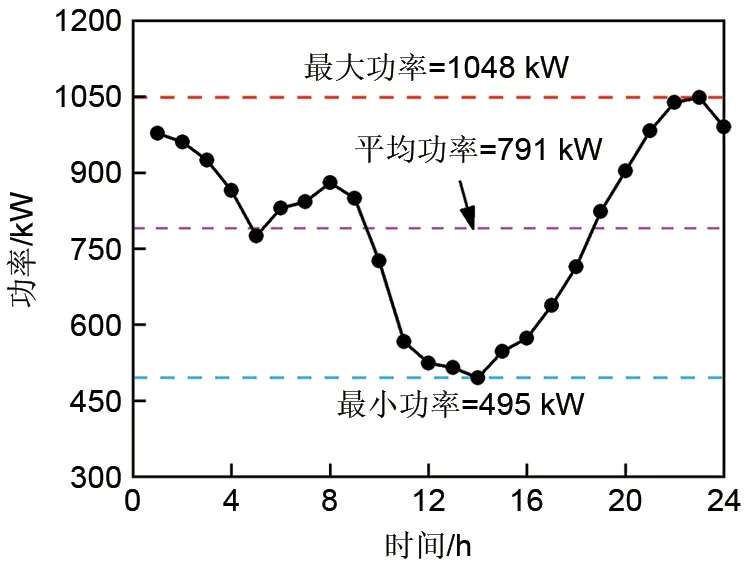
图4 典型小时风机输出功率曲线Fig.4 Typical hour fan output power curve

1.1.2 每小时用户负荷需求

需求侧的电力负荷是随机的和不确定的[15]。为了分析每小时的负载需求，收集了2018年一家工厂用户的历史负载数据，由于设施维护需要仅保留有部分数据，其最大和最小负载需求的值分别为3826 kW和2109 kW。图5为其2018年8月1日到8月5日间工厂的实时负荷需求功率。

图5 8月1日到5日间工厂负荷需求功率曲线Fig.5 Plant load demand power curve from August 1 to 5

显然，实时负荷需求是不确定的。为了应对不确定的负荷需求，相较于文献[16]使用了模糊聚类理论获得典型的每小时负荷需求。本研究主要通过[17]加权平均法(WAM)获得典型的每小时负荷需求。图6描绘了0:00—1:00期间负荷需求的概率分布。

图6 0:00—1:00负荷需求功率概率分布Fig.6 0:00—1:00 load demand power probability distribution

基于概率分布构建小时负荷需求功率曲线，主要步骤包括。

（1）计算每小时负荷需求的边际分布。

（2）获得每小时的概率负荷需求。

（3）根据步骤(2)绘制负荷需求曲线，可以通过以下等式描述，其中PL(t)是时间t的用户负载需求功率，f(t,PLi)是在时间t负载需求等于PLi时的概率。

根据上述步骤，典型小时负荷需求曲线如图7所示，其每小时平均负荷需求3241 kW。

图7 典型小时负荷需求曲线Fig.7 Typical hourly load demand curve

综上，基于风力发电和用户负荷需求建立24小时联合功率分布，具体参数见表2，该分布模型是执行第3节中优化调度策略的基础。

表2 小时负荷需求和风力分布Table 2 Hourly load demand and wind distribution

1.2 压缩空气储能系统模型

CAES系统由：①压缩机组，②电动发电机组，③膨胀机组和④储气罐等组成，其工作示意图见图2。在充电模式下，使用多余的电力来驱动压缩机，将部分弃风量转换为存储在储气罐的压缩空气实现储能；在放电模式下，高压空气通过用于稳定输出压力的节流阀排出，然后进入膨胀机驱动发电机工作。

本文基于以下假设建立CAES系统模型：在各环节气体流通中不考虑漏气；忽略流体在流动、换热过程中的相变及化学反应；不考虑流体在管道中的热量损失和压力损失。

1.2.1 压缩阶段模型

根据热力学模型，压缩功率(充电功率)的数学表达式[18]为

式中，ηch为CAES的充电效率；PCAES,ch(t)为在t时刻CAES的充电功率；Ncom为压缩机级数；γ和Rg分别为其比热容和气体常数，qcom为质量流量；Tcom,out,i和Tcom,in,i为 进 出 口 温 度；πcom,i为i级 额 定 压缩比。

第i级压缩机出口温度为

1.2.2 膨胀阶段模型

膨胀功率(放电功率)的数学表达式[18]为

图8 风电耦合CAES系统工作示意图Fig.8 Working diagram of wind power coupled CAES system

式中，ηdis为CAES的放电效率；PCAES,dis(t)为在时刻t处CAES的放电功率；Nexp为膨胀机级数，qexp(t)为其质量流量；Texp,out,i和Texp,in,i为其进出口温度；πexp,i为i级额定膨胀比。第i级膨胀机出口温度为

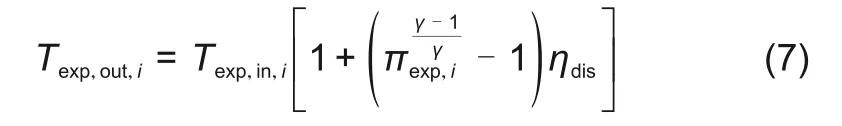
1.2.3 高压储气阶段模型

目前，针对CAES系统中储气罐模型的研究，一般是在热力学基础上通过计算压缩和膨胀工序后的气压差值来进行建模的。但是，考虑到本研究中CAES系统主要功用是电力间的转换，故直接使用系统容量变化值来建立储气罐数学模型。其表达式[18-19]如下

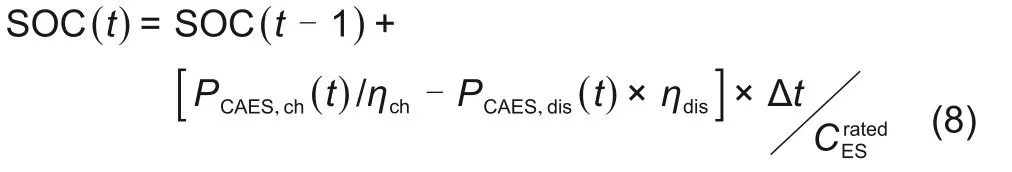
2 确定风电耦合CAES系统优化模型

2.1 目标函数

储能系统的容量配置与其经济性直接相关，因此本文选择净现值(NPV)作为效用函数，通过寿命内预期收入减去寿命内预期成本来计算。具体来说，预期成本来自初始投资、运营和维护成本以及电力不足的补偿成本，另一方面，预期收入主要来自电力销售收入[2]，其表达式为

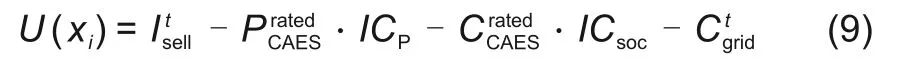
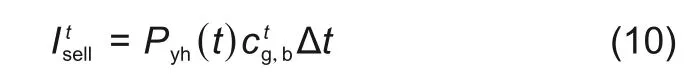
式中，Pyh(t)为t时储能系统的满足用户侧负荷功率；ctg,b为时间t时刻电网上网电价Δt时间间隔为1 h。第二项和第三项中成本系数从一次性安装成本，年度运行维护成本等方向考虑，通过式(11)和式(12)详细描述。

式中，Invc和Invp为每兆瓦时和兆瓦的一次性安装成本；OMc为每CAES系统年运营和维护成本；r为投资利率；Ndays为一年中的天数；l是储能系统寿命(以年为单位)。第四项通过式(10)描述，当系统的输出功率小于电力负荷需求可时，通过本地电网购买缺额电力来缓解电力短缺问题，其表示为

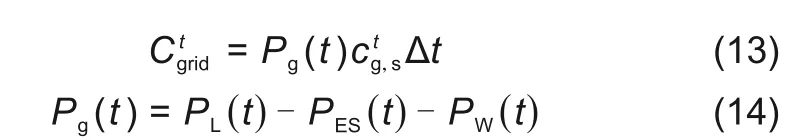
式中，ctg,s为t时电网出售电价，Pg(t)>0时，表示从电网补充功率；PES(t)为t时储能系统的充电功率或放电功率。

2.2 约束条件

根据第1.2节中的系统模型，其优化过程应包括以下约束[10]。

（1）系统功率平衡约束，其是优化容量配置策略时一个重要的因素。考虑到需要协调风力发电厂，CAES系统，负荷需求中心以及电网等单元间的关系，以实现适宜的能量转换和传输，故需要在规划的时间间隔内完成电力负荷平衡，其数学表达式[18]如下

（2）CAES充电和放电功率限制，CAES系统的充放电通过压缩和膨胀气体来实现，受CAES系统额定功率和额定容量的制约，其数学表达式如下

（3）CAES充电和放电状态变量的耦合约束，该约束用于保证表达CAES系统不同时工作在压缩和膨胀阶段，其数学表达式如下

（4）在时间t下，CAES储气容量(SOC)约束，其体现的是CAES系统中储气装置的约束，在正常运行条件下，储气装置是有体积容量限制的，其数学表达式如下

式中，Pdu(t)为CAES系统充满电时丢弃的风电功率；uch(t)为CAES的充电状态变量，1表示充电，否则为0；udis(t)为CAES的放电状态变量，放电时为1，否则为0；η1和η2为储气罐容量的下限和上限。

2.3 求解算法

本节所提出的CAES容量优化配置模型，可以等效为单目标优化问题，采用GA算法进行求解[20]，该算法能够有效应用于非线性和离散的各类实际问题。算法流程图如图9所示，该程序使用MATLAB r2018b进行编码，采用GA算法作为优化引擎，算法设定有初始种群200，交叉概率0.85，变异概率0.2，并在2.5 GHz intel Core i5-7300HQ CPU和8 GB RAM的笔记本电脑上执行。

图9 确定最佳CAES存储规模流程图Fig.9 Flow chart for determining the best CAES storage scale

3 仿真结果分析

3.1 仿真参数设定

表3 储能系统规格[22-23]Table 3 Energy storage system specifications[22-23]

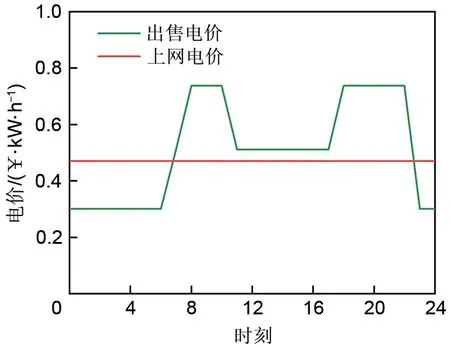
图10 分时电价Fig.10 Time-of-use electricity price

3.2 仿真场景设定

考虑到风电场装配的FD70b风力涡轮机每小时平均输出功率仅为791 kW，而工厂负荷需求已达到每小时3241 kW，故需要维持风电场每时有适宜数量的风力发电机组正常运行，才可保证系统间的电力平衡。鉴于上述原因，逐时分析风机规模对系统运行经济性的影响，确定合理的风机调度策略是具有可行性的。因此，设置多种场景对比选取适宜风电场的风机规模，其场景设置见表4。

表4 场景设置Table 4 Scene setting

3.3 多场景运行下经济性对比分析

不同数量风机作用下，风电耦合CAES系统经济效益变化情况，见表5。无CAES系统时，随着风机数量的增加风电场弃风量逐渐升高，购电成本逐渐减少；配置CAES系统后，同数量风机作用下，有效减少了系统购电成本和风电场弃风量。但需要注意的是，只有合理配置风机数量才能实现整个系统的获利。如场景1，每小时风电场实际输出功率仅为2.373 MW远远不能满足用户需求，出于弥补电力不足造成了高额的购电成本；场景2下，4台风机运行的风电场每小时实际输出功率为3.164 MW接近于工厂负荷需求3.241 MW，在CAES系统作用下弃风量减少3.84 MW·h，节约购电成本4208.9元；场景3和4下，由于风电场风机运行数量增多，使得系统运行和投资成本上升，出现了经济效益下滑的现象。综上，针对负荷需求变化的工厂用户，确定合理的风电场风机运行策略，配置适宜的CAES容量存储规模可有效提升系统的经济效益。在本研究中，针对典型小时负荷需求为3241 kW的用户，采用场景2的配置是可行的，下一节则进一步分析PratedCAES和CratedCAES作为优化变量对系统经济性的影响。

表5 多场景每日收益分析Table 5 Multi-scenario daily income analysis

3.4 最优调度的结果

在本研究中，CAES系统中供给用户侧能量为正，其余为负，即放电功率为正充电功率为负，每日电力调度情况见图11。0:00—4:00，20:00—24:00是夜间风力较大，同时考虑到该时段正处于电网电价峰谷阶段进行多余风力的存储更具有经济价值，故CAES系统以充电为主；11:00—19:00风力输出不能完全满足负荷需求，受限于电网出售电价较高，该部分负荷需求主要以CAES系统放电来满足；从12:00开始，电网售电价格出现回落，其增加了电网购电的优势。如上所述，在双重电价影响下，CAES系统可以自由的执行多余风力的存储和负荷需求的转移，当优化模型评估其利益有损失时会增加储能的释放。

图11 风电耦合CAES系统每日电力调度Fig.11 Wind power coupled CAES system daily power dispatch

在该优化模型下，风电耦合CAES系统运行1天时储气罐内能量变化，见图12。充电阶段，在0:00—5:00内功率由0.70 MW阶梯下降到了0.04 MW，储气罐储气容量由50%上升到90%，这个阶段共充电约1.78 MW·h；放电阶段，在9:00—18:00内系统放电，放电功率在0～1 MW范围变化，储气容量由峰值90%阶梯下降到11.71%。风电耦合CAES系统运行24 h后，储气罐存储容量达到了82.90%处于限定范围内，确保了储能系统周期性、可重复利用的功用，验证了优化模型的可靠性。

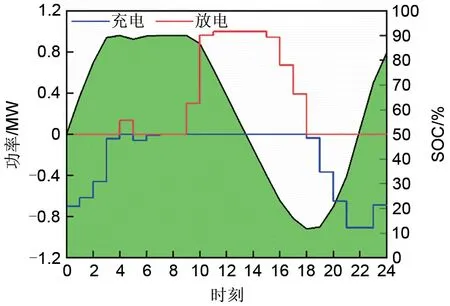
图12 充放电过程中SOC变化曲线Fig.12 SOC change curve during charging and discharging

CAES系统存储规模配置过程见图13。该过程严格执行2.3节的求解算法，在系统额定功率和额定容量限定范围内逐步寻优。如图可见，随着CAES容量的增加，系统总收益先增加后减小，仿真结果显示在A点达到峰值，该点处PratedCAES=1 MW、CratedCAES=6.5 MW·h，其日最大净利润为699.86元。出现上述变化的原因是：CAES存储规模的扩大进而造成系统投资和运行成本大幅度增长，影响了系统经济效益。

图13 CAES系统存储规模最佳配置Fig.13 The best configuration of CAES system storage scale

综上所述，该模型可有效实现风电耦合系统储能存储规模的配置。电力平衡优化结果如图14所示，其是基于场景2的设定实现的。调度结果如下：0:00—4:00、20:00—24:00时间段内，在满足用户负荷需求后出现了多余风力，故通过CAES系统进行存储以减少能量的浪费；6:00后，CAES系统储气罐已达满负荷状态，其需要在优化策略下进行适宜调节，故出现弃风量增大现象；10:00开始，风力减弱，此时由风力发电、压缩空气储能、电网协同运行，为用电用户供电。

图14 电力平衡优化结果Fig.14 Power balance optimization results

4 结 论

为改善风力发电波动性及用户需求不确定性等问题，本文建立了以最大净收益为目标的优化模型，并采用遗传算法求解了CAES系统最佳存储规模，实现了电力和风力间的生产、分配、存储和转换。同时，利用所建立的模型对多场景运行案例进行仿真验证，得到如下结论。

（1）风电场风机运行数量影响风电耦合系统的经济效益，下降时会造成高额的购电成本，上升时会增大风电场弃风量使储能系统投资成本上升，综合分析结果，本文选定4台风机为经济效益最佳数量。

（2）配置额定功率1 MW、额定容量6.5 MW·h的CAES系统可满足典型小时负荷功率3.241 MW工厂用户的电力需求，可有效减少弃风量3.84 MW·h、节约购电成本4208.9元、实现日最大净收益699.86元。

本研究为改善风力和负荷需求不确定性提出了一种CAES系统规模优化配置新方法，为电力调度合理化提供一种新的思路。