基于时空相关性多任务神经网络的交通预测

李松江 祝绍凇 杨华民 王 鹏

(长春理工大学计算机科学技术学院 吉林 长春 130022)

0 引 言

高速路网短时交通量预测已经成为高速公路运营部门在管理过程中研究的核心问题之一。精确的交通状况预测在减少道路交通拥堵、调整人们出行规划，以及提高交通管理维护效率等方面发挥着重要作用。近年来，国内外学者在该领域进行了大量研究，已取得了许多研究成果。目前广泛应用的有历史平均模型、卡尔曼滤波模型[1-2]、神经网络模型[3-4]、支持向量机[5-6]和组合预测模型[7-8]等。但多数模型只利用了目标路段过去时刻的交通量数据，未能充分利用路网内其他相关路段的交通流信息，在一定程度上影响了预测效果。

实际上，由于高速路网的物理特性，区域中通过某路段的交通流与通过其上游n(n≥1)阶邻接路段的交通流在时空上显然是存在关联关系的，在进行高速路网交通量预测时，应充分利用路网的这一特性[9]。国内外学者针对这一特性进行了相应的研究，并取得了一些研究成果。熊亭等[10]对布设在美国华盛顿州I-5高速公路北向车道上的3个线圈检测器数据进行周期性分析，将目标路段上下游的车流量及车速作为空间特征向量，利用SARIMA-RF组合预测模型进行目标路段的交通量预测；李巧茹等[11]将时间与空间序列流量观测值作为支持向量机的训练样本，通过路网路段历史时刻的空间序列得到空间序列的预测值，使用空间序列预测值对交通流时间序列预测结果进行修正，动态调整其对未来预测的影响。上述文献都取得了较好的预测效果，但预测模型仍仅限于利用单点附近的交通流信息，未能拓展至区域网络。

针对上述问题，本文提取能体现高速路网拓扑关系的空间权重以及描述路网时空状态的时间权重，利用高斯加权欧氏距离剔除了路网区域内的非时空相关路段，通过多任务循环神经网络对目标路段的交通量进行协同预测。实验结果表明，将时空相关路段的交通量预测作为目标预测任务的额外任务，对于目标路段交通预测准确度具有提升作用。

1 数据准备与时空特征变量定义

1.1 数据准备

本文研究的高速路网短时交通量预测模型，需要充分考虑路网内的其他路段与历史时段的交通量对目标路段的影响。选取吉林省某区域的部分路网作为研究对象，交通流示意图如图1所示。图中的每个圆圈节点表示一个道路交叉点，箭头表示交通流的方向，交通流从上游链路到达对应的道路链路[12]。通过整理该区域自2018年5月7日到6月3日总计28天的路网收费数据，最终以5 min的时间间隔确定了路网内34条路段的交通量数据与平均车速数据。如图2所示，将高速公路CB中长度为18.46 km的路段“0”记为目标路段。

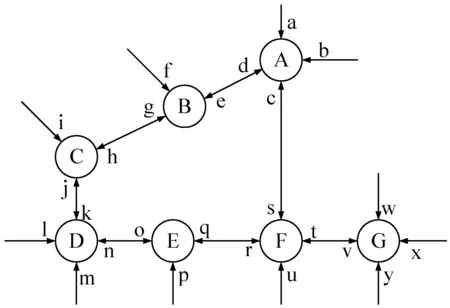
图1 路网交通流示意图

图2 目标高速公路示意图

1.2 时空特征变量定义

在高速路网中，路段交通流受多种因素的影响。由于区域路网内路段分布广泛、连接情况多样，导致路网空间状态主要受两个明显的空间因素影响：路段间距与路段连通度。

定义1设d为路网中的路段与目标路段之间的物理距离，本文通过计算路段的中点之间的距离进行统计。

定义2设g为路网中各路段的连通度等级，第一级(g=1)为与目标路段处于同一高速公路的路段；第二级(g=2)包括与目标路段所在高速公路存在交叉点公路上的路段；第三级(g=3)对应于第二级存在交叉点公路上的路段。其余的等级(g=4,5,6,…)也有类似的描述[13]。

图3 高速路段连通等级示意图

除了固有的静态影响因素外，路网内各路段间的相关系数也可以作为描述交通流之间影响程度的动态标准。

定义3设r为目标路段与路网其他路段交通量时间序列的相关系数，其计算式表示为：

(1)

式中：x和y分别表示两个路段的交通量时间序列；m为时间序列的长度。

定义4设c为确定目标路段与其他相邻路段之间的空间相关性的准则(即等效距离)，其计算式表示为：

(2)

式中：g为路网层次结构中各路段的连通度等级；d为路网中的路段与目标路段之间的物理距离；r为目标路段与路网其他路段交通量时间序列的相关系数。等效距离与路段间距和路段连通度呈正相关，与路段间的相关系数呈负相关。

定义5将描述路网交通状态的二维时序矩阵设为V(m,n)，表示为：

(3)

式中：m为时间序列的长度；n为路网中路段序列的个数(包括预测路段)；状态矩阵的元素表示在一定的时间步长内各路段交通流的平均速度。V(m,n)利用m个时间步长和n-1个邻近路段的数据来确定整个路网的交通状态。

2 基于时空相关性的交通量预测模型

本文通过构建多任务循环神经网络模型对目标路段未来时刻的交通量进行协同预测。多任务学习中将目标路段未来时刻的交通量预测作为预测模型中的主要任务，同时认为预测其相关路段的交通量与主要任务有一定的关系，故选择它们作为额外任务。额外任务与主要任务具有共同的归纳偏置，可以提高主要任务的预测精度。依据图4所示的基于时空相关性的交通量预测流程构建出对应的预测模型，模型主要分为两个部分：① 利用时空相关性确定连通路网中的相关路段；② 通过多任务循环神经网络对目标路段的未来交通量状态进行预测。

图4 基于时空相关性的交通量预测流程

2.1 获取路网时空相关路段

众所周知，物理距离代表了路网的固有空间特性，但这一概念并没有反映路段之间的动态空间属性，即交通流特性。本文将实际路网中采集的静态物理数据与由路段时间序列计算的相关系数相结合，得到同时具有物理与数据属性的复合变量，称为路段间的等效距离。等效距离的计算步骤如下：

(1) 根据划定的路网区域，确定区域中目标路段与其他连通路段的连通度g与路段间距d。

(2) 根据当前时刻路网时空状态的时间步长，计算目标路段与其他路段交通量时间序列的相关系数r。

(3) 通过式(2)计算路段间的等效距离。

本文通过探究区域各路段与目标路段交通量状态变化的相似度确定路网中的时空相关路段。在获得各路段具有空间特性的等效距离后，利用由平均速度组成的时空状态矩阵识别路网的交通状态。由于时空变量的不同度量标准之间存在差异，故通过高斯加权函数将等效距离附加到每条路段对应的时空状态向量上，以时间维与空间维相结合的方式确定目标路段与其他路段之间的时空相关性。然后将现在时刻与历史时刻时空状态向量的欧氏距离作为判断每条路段状态变化程度的标准，进而得到路网区域中目标路段的时空相关路段。确定时空相关路段的步骤如下：

(1) 利用高斯加权函数确定路段的空间权重。将空间加权矩阵定义为W，其元素分别定义为wi，则W表示为：

(4)

式中：ci为编号i的路段与目标路段间的等效距离；根据实测数据计算出空间加权参数中方差a的值。

(2) 利用高斯加权函数确定路段的时间权重。将时间加权矩阵定义为Q，其元素分别定义为qj，则Q表示为：

(5)

式中：tm为当前时刻的时间步长；tj为tm前m-j时刻的时间步长，与m-j时刻计算平均速度的时间步长相对应；根据实测数据计算出时间加权参数中方差b的值。

(3) 确定路网区域的交通状态。将式(4)与式(5)得到的空间权重与时间权重通过矩阵乘法的形式附加到路网时空状态矩阵上，得到具有时空属性的路网状态矩阵X，加权公式表示为：

X=Q·V·W

(6)

式中：Q为时间加权矩阵；V为路网状态矩阵；W为空间加权矩阵。

(4) 计算路段交通状态变化程度。设X与Xl分别为当前时刻与第l个历史状态下的路网时空状态矩阵，Xi为第i条路段的时空状态列向量，将第i条路段在两个时刻下时空状态列向量的欧氏距离作为判断该路段交通状态变化程度的标准，记为Si，表示为：

(7)

2.2 多任务循环神经网络

在传统的神经网络中，相邻的隐层间完全连接，但是同一层内的节点间没有连接，而交通量的时序数据在描述交通流变化时前后存在明显的交互。循环神经网络(Recurrent Neural Network)拥有一种特殊的神经网络结构，其隐层节点之间是相互连接的，可以对前一时刻的信息进行记忆并应用于当前输出的计算中，因此能够处理连续和相关的任务。RNN的典型网络结构如图5所示。

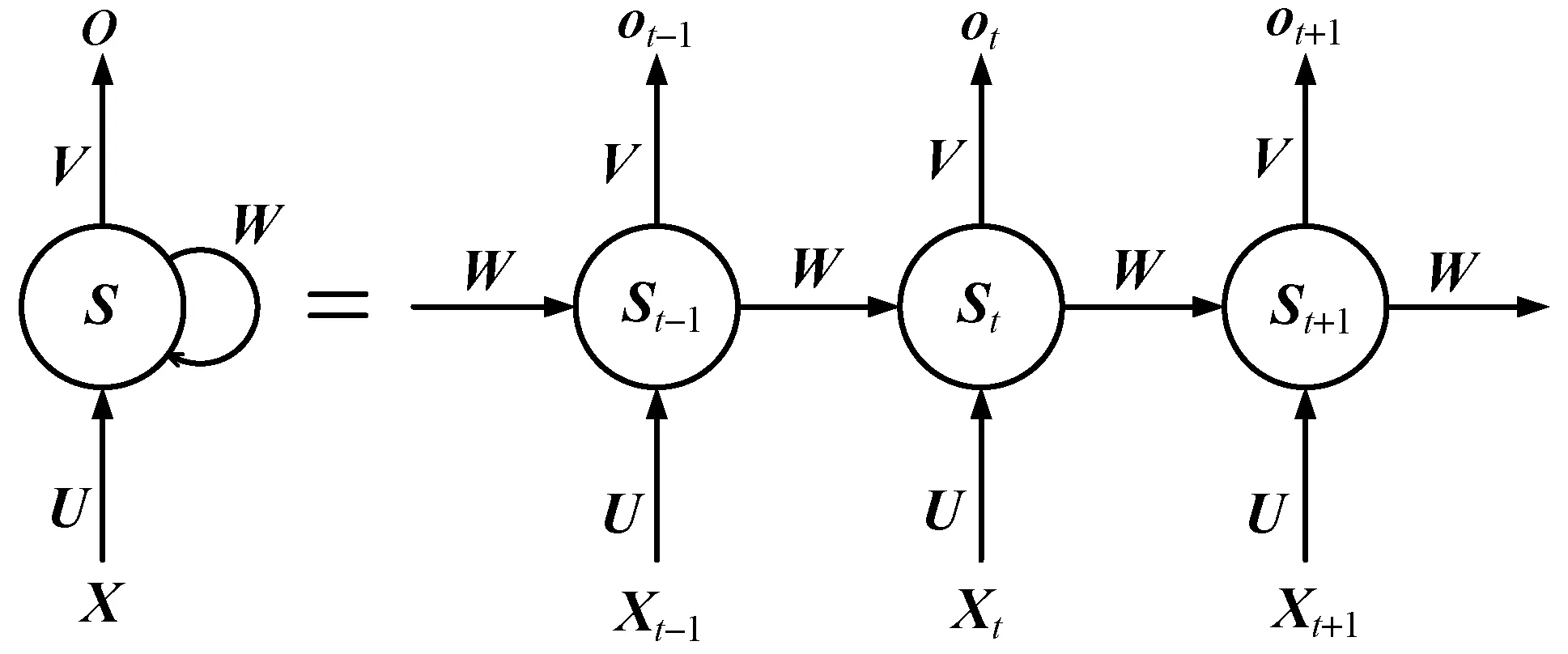
图5 循环神经网络结构

图5中RNN的数学模型可以表示为：

Ot=g(V·St)

St=f(U·Xt+W·St-1)

(8)

式中：Xt是输入向量；U是输入层到隐藏层的权重矩阵；V表示隐藏层到输出层的权重矩阵；W表示用于隐藏层自身递归的权重；Ot为预期的输出向量；g和f表示激活函数Sigmoid。

交通系统作为一个高度相关的网络，为使用来自网络相关部分的共享知识，应从网络的角度进行交通量预测。使用欧氏距离计算每条路段当前状态与历史状态之间的交通参数距离，识别出区域路网内与目标路段交通状态变化相似的时空相关路段。本文利用多任务学习的归纳转移机理，选取与预测目标路段未来时刻交通量相似的多个训练目标，根据目标间特定的相关信息来提升学习系统的泛化能力。将路网内时空相关路段的交通量预测作为多任务学习的额外任务，通过将多任务学习与循环神经网络进行结合，构建如图6所示的网络预测结构，对目标路段进行短时交通量预测。其中共享隐层可以提取路段之间共享的空间信息，使每一项预测任务作为其他任务的辅助，充分利用了路网的空间信息。而特定任务层可以拆分每一个任务，对其中的与其他任务不同的特定信息进行学习。

图6 多任务循环神经网络预测

(9)

本文通过使用多任务循环神经网络模型对目标路段的下一个时刻的交通量进行预测。多任务学习共同训练模型并共享隐藏层的权重，相较于单任务学习只需要训练一个模型，该模型将具有相似权重分布的任务组合在一起，可以根据任务之间的共同特性与每个任务的独有特性提高预测性能，故该模型比单一路段的交通量预测模型具有较高的预测精度。

3 实验与结果分析

3.1 实验描述

本文针对高速路网短时交通量预测问题进行了研究，提出基于时空相关性的多任务循环神经网络协同预测模型。实验主要包括两个部分：(1) 分别计算出当前时刻与历史时刻所有路段的交通状态向量，从而确定路网区域内的时空相关路段；(2) 将相关路段的交通量预测作为多任务学习的额外任务，通过构建神经网络完成对目标路段交通量的协同预测。

为验证该预测模型的适用性及准确性，本文选用吉林省的部分高速路网作为研究对象，并选取自2018年5月7日至5月27日共3周的交通量时间序列数据作为模型的训练集，用于模型的构造与训练；选取5月28日至6月3日1周数据作为测试集，用于对模型进行验证。

3.2 评价指标

本文选取的性能指标参数为：均方根误差(RMSE)与绝对百分误差(MAPE)定义如下：

(10)

(11)

3.3 实验结果分析

实验的前半部分为计算路网区域内所有路段交通状态变化的欧氏距离。利用不同数量的路段经过足够次数的训练后，损失函数呈现出一定的变化趋势，如图7所示。最终将相关路段交通状态变化的阈值确定为66，并得到14条与目标路段具有相似时空特性的路段，各路段参数如表1所示。然后利用这些相关路段的交通量时间序列作为多任务循环神经网络的输入，通过共享隐藏层参数实现对目标路段的未来时刻交通量进行协同预测。

图7 损失函数的变化趋势

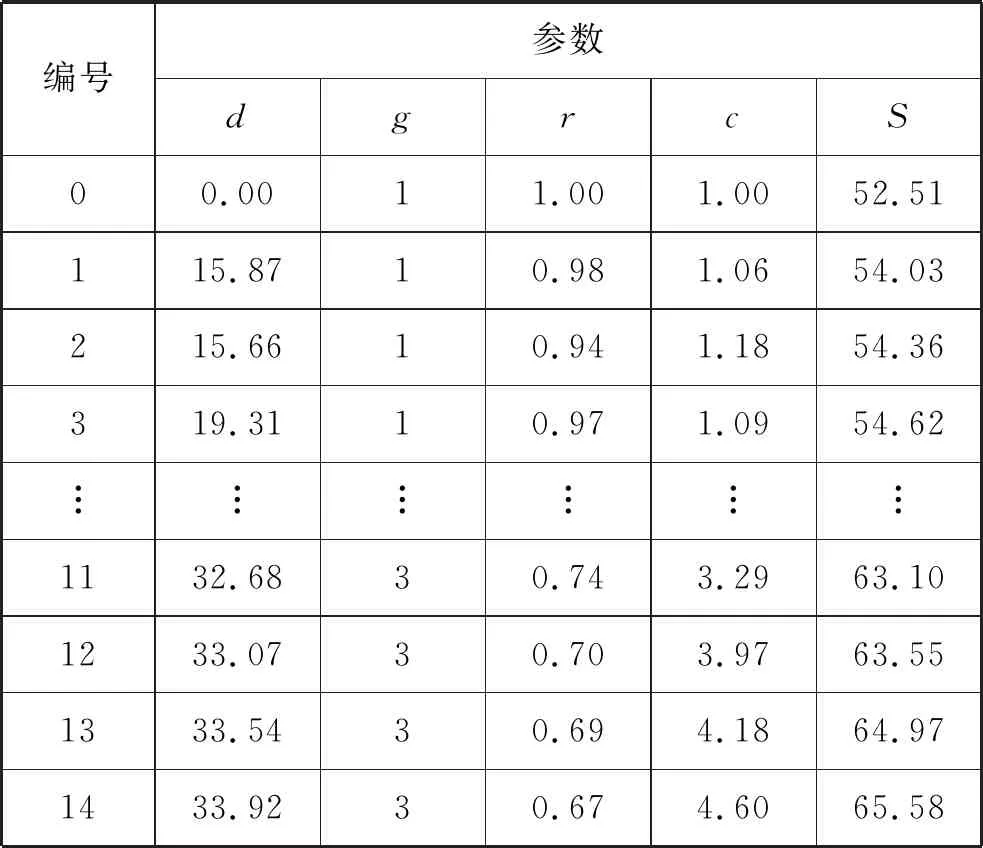
表1 目标路段的时空相关路段

利用TensorFlow构建出多任务循环神经网络交通量预测模型。构建包含三个共享隐层结构的神经网络模型，其中隐层包含神经元数目分别为100、200、300，特定任务层神经元数目为300。将Sigmoid函数作为输入层和隐藏层之间的特定激活函数，权值初始化函数为orthogonal。将相关路段的时间序列矩阵归一化后作为多任务循环神经网络的输入层数据。通过观察网络训练误差的变化，选取1 000次迭代作为最大的训练次数，学习率为0.025，批大小设置为64。

本文通过两部分验证基于时空相关性的多任务循环神经网络交通量模型的预测性能，一是将该模型分别与引言部分的两种模型和传统的时间、空间模型进行比较，各模型的性能指标对比如表2所示；二是将由时空相关路段训练的模型与由路网内所有路段训练的交通量模型进行对比。

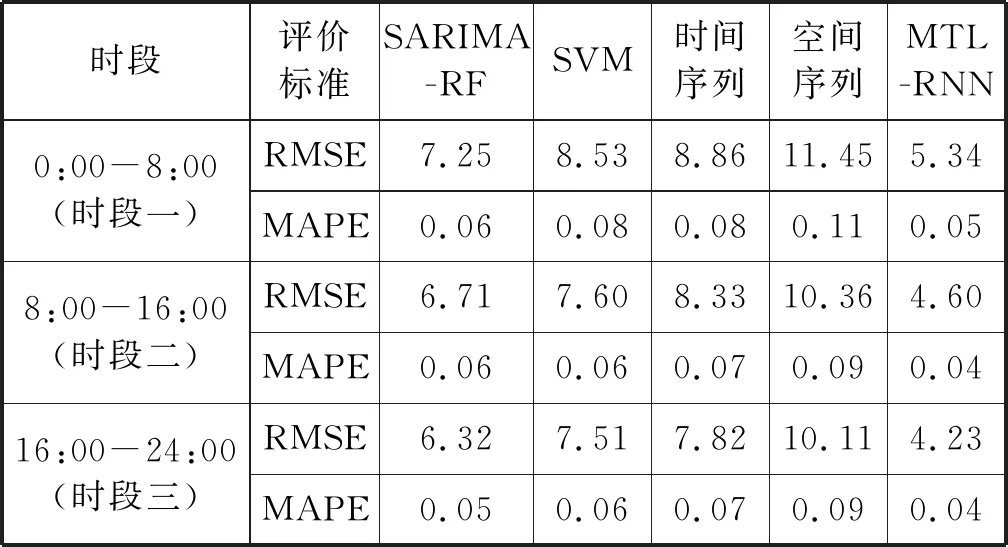
表2 性能指标对比

基于时间序列或空间序列的单变量预测模型在三个时段中的预测结果与实际交通量相比有较大的差距，而SARIMA-RF与SVM模型的预测误差在每个时段都多于MTL-RNN模型0.02左右，因此基于时空相关性的交通量预测模型在三个时段的性能指标中的表现最佳，该模型在复杂路网的交通量预测方面有较高的精确度。将上述三种模型的预测结果分别与实际交通量作比较，图8为五种模型在2018年6月4日内的三个时段的目标路段交通量预测值和真实值的对比结果。

(a) 时段一对比情况

基于时空相关性的交通量预测模型的误差明显小于基于时间序列和空间序列的交通量预测模型，而且与SARIMA-RF和SVM两种模型相比，该模型在任何时段中都具有良好表现，更加接近实际的交通量变化曲线。由此可推测出，通过路网中各路段的过去时刻的交通量实现对目标路段未来时刻交通量的预测，可以充分利用路网的时间特性与空间特性，在一定程度上可以明显提高交通量预测的准确度。

最后，为验证不相关任务可能会对模型训练产生的负迁移现象，选取路网中的时空相关路段与由所有路段训练的交通量预测模型进行准确度对比。如图9所示，由路网中相关路段训练的交通量预测模型的预测准确度最终维持在92%左右，而由所有路段训练的模型的准确度在88%左右，故只有将相关的任务集成到一个组中，才能够更好地提高整体性能，无关任务的共享信息可能会降低模型的性能。

图9 不同等级路网的预测准确度对比

4 结 语

本文针对高速路网短时交通量预测，提出一种基于时空相关性的多任务循环神经网络预测模型。其中针对传统的交通量预测中忽视路网邻近路段数据的问题，提出一种计算路网中路段时空相关性的方法。通过量化路网物理结构中的路段距离、连通度与路段间的相关系数得到每条路段对应的空间权重，比较各路段不同时刻的交通时空状态向量，得到目标路段的时空相关路段。然后将相关路段的交通量预测作为相关任务与目标路段放到一组联合训练，通过共享隐藏层提高神经网络预测性能。实测交通量数据验证的结果表明，本文提出的预测模型预测值和真实值吻合效果较好，是一种有效的交通量预测方法。