基于数据挖掘的空气质量预测模型研究*
周凯 刘萍
(陆军炮兵防空兵学院 合肥 230000)
1 引言
“绿水青山就是金山银山”,十八大以来,人们逐渐把生态文明建设放在突出位置。在各种有力措施的治理下,空气质量作为生态文明建设的重要一环,其情况得到了有效改善。但大气污染物对身体健康的影响还持续存在。像华北地区,进入秋冬季,雾霾便会笼罩全城,引起一系列呼吸道疾病,严重的造成交通事故危及生命。据世界卫生组织称,每年因空气污染导致疾病而死亡的人数高达700万[1]。因此在大数据技术浪潮兴起的今天,如何通过数据挖掘和分析对未来空气质量,进行实时有效的预测预警,以避免各种灾难的发生,成为一个亟待研究的课题。
数据挖掘技术在20世纪90年代得到了飞速的发展,所谓数据挖掘,顾名思义即是在大量的关系或非关系数据库中发掘出隐含的、未知的有价值信息。它是一种决策支持过程,主要为决策者提供信息支持。主要基于机器学习、人工智能、传统统计学等数理手段。通常由数据准备、数据挖掘和数据分析三阶段组成。空气质量数据经过数十年的积累,其隐含的价值是可观的。空气质量指数(AQI)是衡量一个地区此刻空气质量水平的一个重要指标,指数越大,危害越大[2]。
空气质量数据是典型的时序数据,主要来自地面监测、气象卫星等采集站点。通过对空气质量数据进行数理分析已经成为空气质量预测的可行性途径之一。传统的空气质量预测主要分为数值预测和统计学预测两种,所谓数值预测过去几十年主流的一种预测方式,它主要是通过已有的空气质量数据,推导总结出一系列的物理学和化学状态方程,这些方程通常是高阶微分方程,通过导入相应参数得到未来空气质量数值,但这种预测方式需要规模庞大的计算力,而且考虑的影响方面相当有限,比如像人力活动等,数值预测的参数就很难把握并量化。而统计学预测则是通过数学建模分析已有数据,像非线性数值分析、多元统计、灰色分析、车贝雪夫展开等,但统计学预测存在周期长,操作复杂等限制,难以及时迅速准确地提供空气质量数据的相关信息。随着时间的推移和空气质量数据采集处理技术的多元发展,人们开始逐步采用机器学习等新技术进行空气质量数据的预测以弥补传统预测方法的不足。但传统机器学习等预测方法一般采用的是批处理的学习和预测方式,即在一次样本学习和预测后,便不会对新样本进行学习,这就加大了空气质量预测的误差,偏离了实时预测的轨道,很难有效地应用到实际工程之中[3]。
基于空气质量预测的实际需求,本文在前人研究的基础之上,对比、研究和采纳不同计算框架的优缺点,选取两种分别代表不同类型架构的模型进行空气质量预测。以寻求一种理想的空气质量预测模型。
2 模型原理
2.1 ARIMA原理
为了对比不同模型在预测上的精度优势,我们首先比较传统的时间序列分析法,ARIMA(自回归移动平均模型)是传统统计模型最常见的时间序列预测模型。自20世纪70年代提出后,与不少算法模型组合在预测领域取得瞩目的成绩,其基本思想是将时序数据看成一个随机序列,通过数学模型对其内部构造和复杂特性进行近似描述,以最小方差为目标的最佳预测[4]。时间序列的分析主要从频域和时域两种角度进行分析,频域分析在此不做赘述,
在时域方面,如果时间序列特征随时间而变化,则可说时间序列是非平稳的,反之是平稳的。如果去除均值和确定性因素的随机过程可以用式(1)表示[5]:
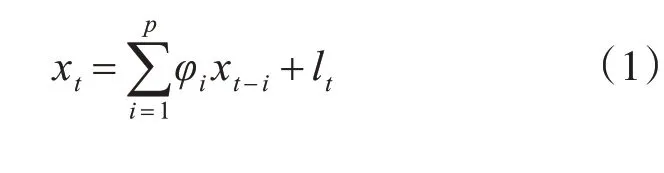
则可说该过程是p阶自回归过程,其中φi是自回归参数,lt是白噪声,可用AR(p)表示。

如果去除均值和确定性因素的随机过程可用上式表示,则称该过程为q阶移动平均过程,其中θi是自回归参数,lt是白噪声。如果去除均值和确定性因素的随机过程由上述两过程共同表示,就可称其为自回归移动平均过程[6],表示如下:
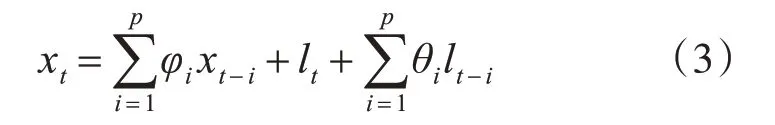
差分过程为现实值与滞后值的差为固定值的幂,几次幂就称为几次差分。如果一个随机过程经过d次差分后变换为一个平稳的自回归移动平均过程,则称该过程为单积自回归移动平均过程,ARIMA预测模型的一般形式如下:

其中,p表示预测模型中采用的时序数据本身的滞后数,d表示时序数据需要进行几阶差分化,才是稳定的,q表示需要移动平均的阶数。空气质量数据是在固定间隔的时间差采集的离散数据,其变量前后必然存在某种联系,ARIMA预测正是寻找这种联系对未来一定时间内的变量进行预测[7]。
2.2 GRU神经网络原理
实现神经网络在时序问题上的应用,绕不开对递归神经网络的研究,递归神经网络RNN也叫循环神经网络,其在结构设计上与传统的前馈式神经网络不同,它也由输入层、隐含层和输出层组成。它考虑到前置样本对当前样本的影响,突出时序对模型预测的作用[8],其数学表达式为
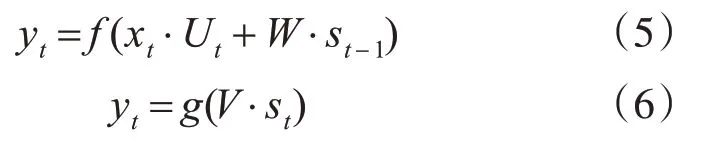
其中,V、W和U分别为输出层权值矩阵、上一层隐含层作为这次输入的权值矩阵、输入层权值矩阵,f和g都为激活函数,st是隐含层状态,xt是输入值。
其中LSTM(长短期记忆)网络为典型的递归神经网络RNN的一种变型,标准RNN中只有一个神经元细胞,一个隐含层进行学习,这样由于在结构上的限制就会在长期记忆方面存在一定的不足,为了实现长期记忆,LSTM在RNN的基础上,增加了记忆单元[9]。
LSTM网络在结构增加门单元,来控制前置信息影响力的大小,实现了对长距离数据对现时数据的有效影响。设置了三个门,这三个门分别是遗忘门、输入门和输出门。每个门实现不同的功能,其中遗忘门控制保留多少状态到目前时刻;输入门控制输入多少当前时刻到当前状态;输出门控制当前时刻的输出[10]。基本公式如下:
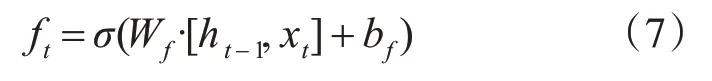
σ单元输出0到1的值,可以通过权值控制每部分输入的量。遗忘门,读取输入xt和前置神经元的h信息,并通过函数值确定要丢弃多少信息。

输入门,通过控制量函数和tanh函数更新细胞状态。
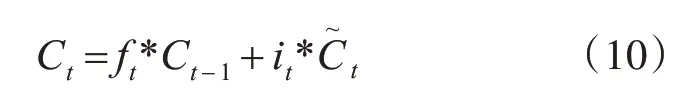
输出门,控制旧细胞状态,将细胞旧状态通过权值控制,忘记需要丢弃的信息,加上新的候选值,旧细胞状态得以更新[11]。

最后的输出为ht,通过一个权值控制层确定哪些细胞状态输出出去,然后将旧细胞状态通过tanh处理后与输出相乘确定最终输出。
LSTM是RNN的变体,GRU则是LSTM的变体,LSTM实现了对远距离依赖的有效处理,GRU则实现处理速度的提升。GRU在网络结构上与LSTM类似,但它只有两个门,它们分别是更新门和重置门。更新门控制先前状态的保留,其值越大,先前状态的影响就越大。复位门控制新输入与先前状态的关系,其值越小,记忆先前状态影响越小。公式如下[12]:


图1 GRU单元结构
3 实验与结果分析
3.1 数据准备与分析
选取北京市2014年1月1日~2014年12月31日的AQI小时数据作为各个模型的研究对象,经过数据缺失值和异常值处理后,一共得到8760条数据。选取的AQI数据是典型的时序数据,符合各时间点上数值序列的特征。本文对一年之中的AQI时间序列作二维曲线图,XY轴分别表示测量序列及浓度值,便于形象直观地展现出AQI的变化规律。
为了方便所选模型训练学习,减少数据偏移、幅度缩放、线性趋势和噪声对后续计算的影响。对所选数据进行归一化处理,公式如下:

3.2 基于ARIMA时序分析预测的空气质量预测模型
基于ARIMA的空气质量预测模型我们选取后280个样本数据进行模型预测,其基本预测步骤可以分为以下四步。
1)首先考察空气质量数据序列是否平稳,观察是否具有季节性,是否为白噪声,依据空气质量数据的ACF(自相关)系数和PACF(偏自相关)系数我们得到图2。
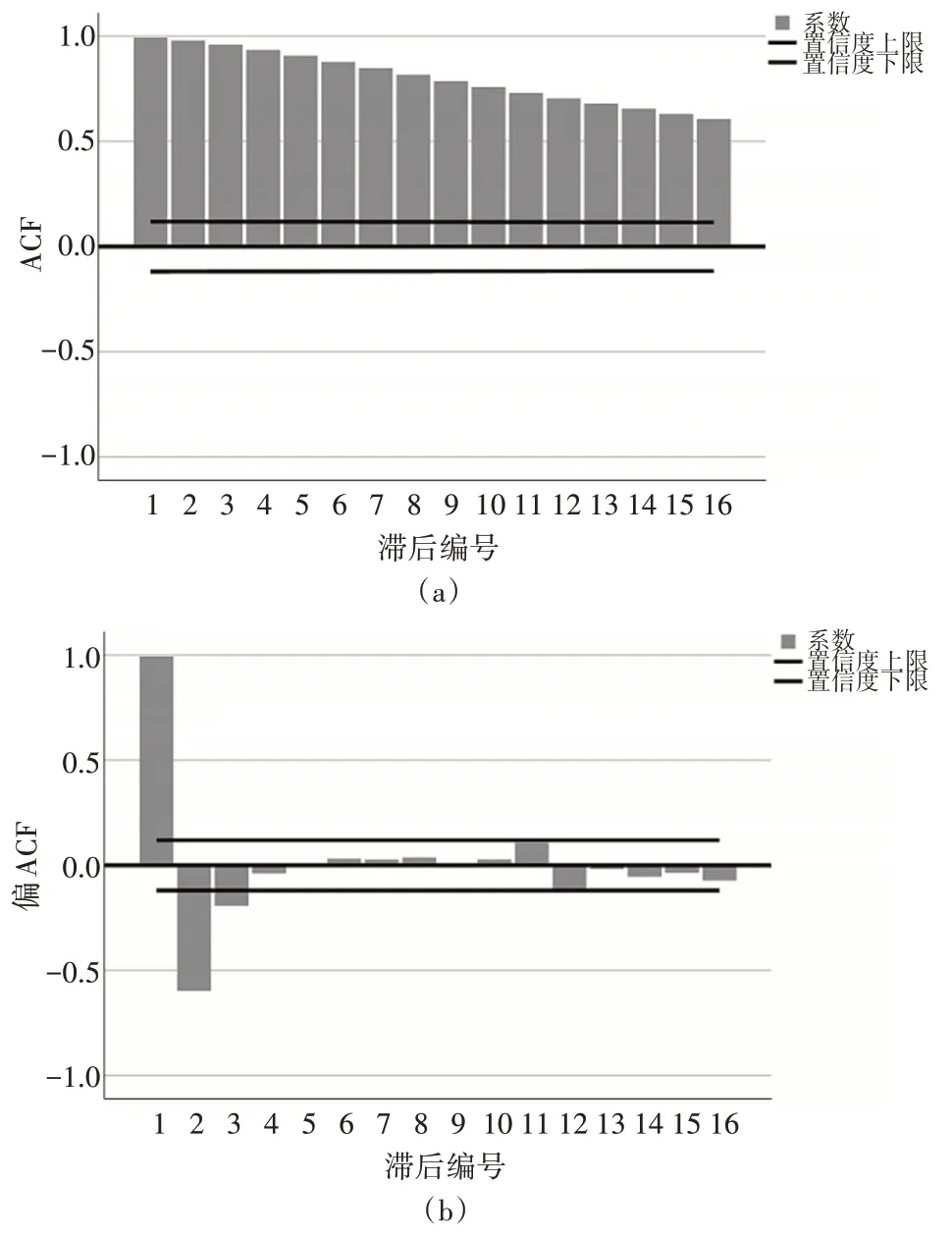
图2 自相关与偏自相关图
在自相关图系数是一个衰减的趋势,我们可以判定为拖尾,偏自相关图在3阶长的时候系数趋于零,可以看出是截尾。因此我们可以判定空气质量时序数据是不平稳的,需要进一步作差分分析。
2)空气质量数据平稳处理。虽然空气质量数据受季节影响,但在图形曲线中并没有呈现季节性变化,我们只考虑通过差分方法使时间序列平稳,分别尝试差分阶数为1、2、3、4,绘制时序图如图3。
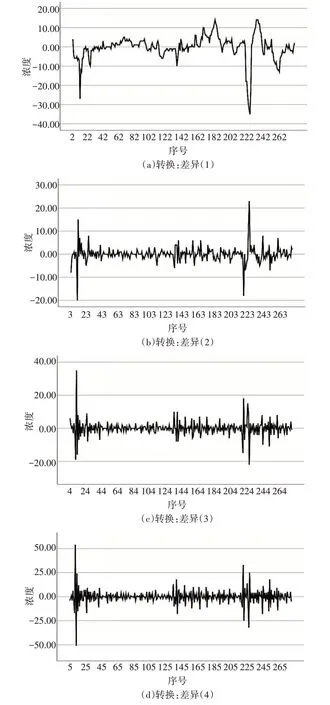
图3 差分图
从经过差分处理的图中,我们发现当差分阶数取4时时序数据趋于平稳。
3)确定ARIMA模型参数及类型,空气质量时序数据平稳处理后,再次通过绘制自相关和偏自相关图,通过下图可知,平稳序列的自相关函数和偏自相关函数均为拖尾,因此我们选用ARIMA模型,偏自相关图在滞后为5以后趋于零,我们暂定P参数为5;自相关系数图中显著不为0的自相关数为2,我们暂定q参数为2,至此我们选择模型ARIMA(5,4,2)。
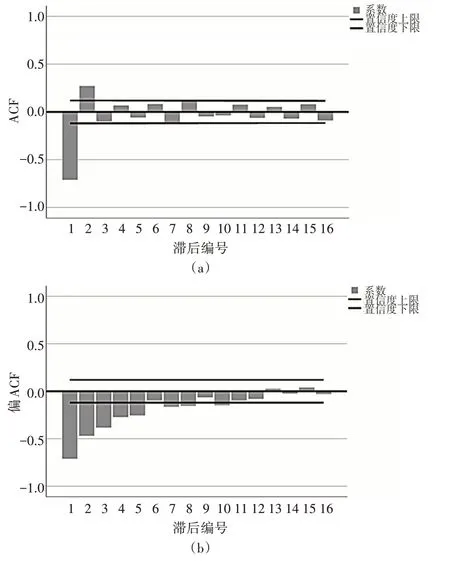
图4 4阶差分后的自相关和偏自相关图
4)根据选定模型进行预测分析。通过模型代入,给出ARIMA残差自相关和偏自相关函数图,从图中可知ACF和PACF图皆没有明显拖尾和截尾,表明预测模型的选取是恰当的。
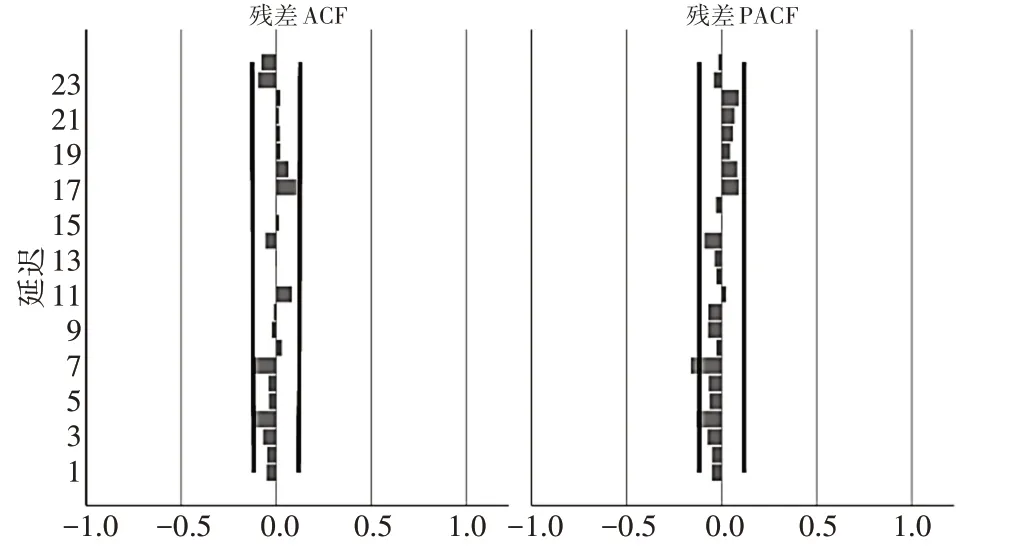
图5 ARIMA残差相关函数图
将原始数据代入模型,我们得到ARIMA拟合预测图,从图中我们可知,拟合值与输入值拟合效果较好。拟合度均方误差3.664,平均绝对误差均值1.975(如表1所示),达到了拟合的预期。然后对后12h进行预测,从结果我们可以看出在前3h置信区间较小,预测精度较高,但随着预测时长的增长,ARIMA空气质量模型的置信区间随之增大,预测精度减低。如果我们需要实现长期预测,还需寻求对远端样本有明显精度预测的模型。

表1 模型拟合统计
3.3 基于GRU的空气质量预测模型
根据前文数据样本分析,我们知道选取的AQI样本为单纯的时序样本,所谓AQI指数是将六种主要污染物中最高的污染指数作为AQI指数,基于上述分析,AQI数据样本的时序分析没有其他变量可以输入,我们选取后8000个样本作为训练样本,用后48h的数据作为样本检测。GRU空气质量预测模型的学习衰减率选为0.002,隐含层单元设置为9,经过训练5000次,可得空气质量预数据在训练计算过程中损失函数情况[13]。

表2 GRU模型训练损失函数值
经过样本训练5000次,模型损失函数值逐渐减少,当训练5000次时损失函数值为0.3012,使用经过训练的模型对指定48h时间步长进行预测,预测结果对比图如图6。
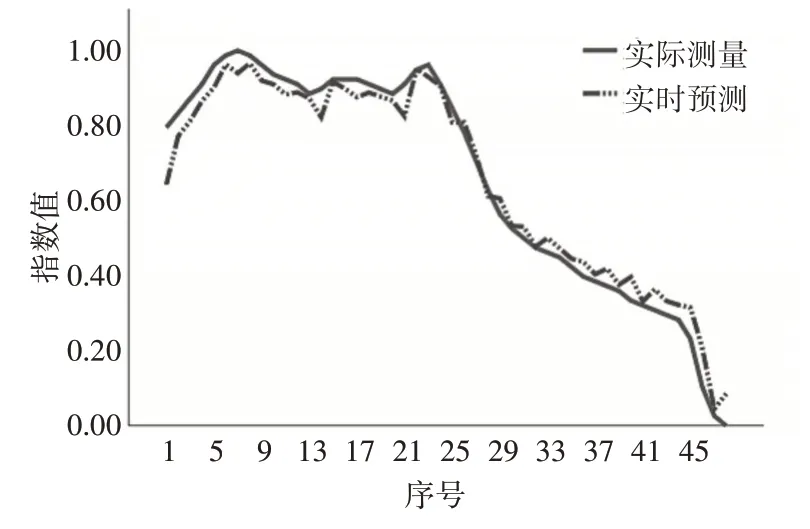
图6 GRU空气预测模型精度对比图
图中实线为实际测量,虚线为实时预测数值。可以看出,在输入数据后得到的48h内的预测结果与实际结果较吻合,证明本文提出的预测模型有较好的预测精度,实现了短期预测的设计目的。说明本文提出的模型切实可行,到此证明了预测模型的可行性,然后将提出的两种模型进行对比[14]。
对比方法我们采用均方根误差法进行对比,均方根误差法(RMSE)是通过预测值减去实际值,将差平方后累加,除以样本个数,最后将商开方,具体公式如下:

其中y1为预测值,y2为实际值,d为样本个数。通过均方根误差可以很好评价一个模型预测精度的好坏,其计算值越小,预测能力越好。表3为两种预测模型均方根误差比较[15]。

表3 预测模型RMSE对比
通过表3,我们对两种预测模型进行均方误差对比,发现基于GRU网络的预测模型在空气质量预测方面有较突出的记忆能力和通用性,对提高空气质量模型的预测精度有很高的学术价值。
4 结语
本文根据空气质量时序数据的特点,分析了提高空气质量预测精度的必要性,总结了前人经验,先对空气质量数据的平稳性进行了分析,随后根据ARIMA模型建立步骤,进行时序数据平稳化,根据自相关和偏自相关图确定ARIMA模型,进行了拟合预测;随后从新兴循环神经网络的角度出发,提出了一种基于门控循环单元网络的预测模型,通过样本选择后进行了预测。实验很好地证明了本文提出的模型通过各种参数设置,其可行性和出色的性能是确实存在的。并计划在将来合并更多种类的深度学习模型并应用更多最先进的机器学习算法,预测更丰富的空气质量数据,为进一步设计出一个具有实用性的空气质量预测系统打下了坚实的理论基础。

